* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 5 - web page for staff
Superconductivity wikipedia , lookup
Schiehallion experiment wikipedia , lookup
Photon polarization wikipedia , lookup
Density of states wikipedia , lookup
Circular dichroism wikipedia , lookup
Electromagnetism wikipedia , lookup
Magnetic monopole wikipedia , lookup
Relative density wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Field (physics) wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
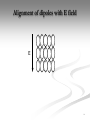
Lorentz force wikipedia , lookup
Electrical resistivity and conductivity wikipedia , lookup
Maxwell's equations wikipedia , lookup
ENE 325 Electromagnetic Fields and Waves Lecture 5 Conductor, Semiconductor, Dielectric and Boundary Conditions 1 Review (1) The electric potential difference Vba is a work done by an external force to move a charge from point a to point b in an electric field divided by the amount of charge moved. b W Vba E d L Q a The electric potential is the same no matter which routes are used. Only displacement distance (shortest route) matters 2 Review (2) Conductors and Ohm’s law Current, I is defined as the amount of charge that passes through a reference plane in a given amount of time. dQ I dt Ampere. Current density, J is defined as the amount of current per unit I J S A/m2 area the relationship between I and J, I J S s convection current J v v conduction current J E 3 Outline Conductor and boundary conditions Semiconductor and insulator 4 Conductors and boundary conditions charge density is zero inside a conductor. Surface charge density DS is on the conductor surface. An electric field inside a conductor is zero. + + + + + Ds=0 E=0 + + + + + outside charges cause an electric field. + 5 Tangential and normal fields. The electric field on the surface can be divided into two components. tangential electric field, Et, = 0 for an equipotential surface normal electric field, En En E Et 6 Boundary conditions (1) Consider a conductor-free space boundary E dl 0 From a h b w d c 7 Boundary conditions (3) Consider Gauss’s law D dS Q From s Dn D Dt 8 Boundary conditions (3) For conductor-free space boundary conditions (B.Cs.) Dt = Et = 0 Dn = 0En s 9 Ex1 Let V 100e5 x sin(3 y ) cos(4 z ) V and let a point P(0.1, /12, /24) locate at the conductor-free space boundary. At point P, determine a) V b) E 10 c) En d) Et e) S 11 Semiconductors Electron and hole currents conductivity ee hh mobility is 10-100 times higher than conductor. electron and hole density depend on temperature. Doping is the process of adding impurities to a semiconductor to alter the polarity. 12 Dielectric or insulator + + + - - - + - - + - + + - + no free charge microscopic electric dipoles energy stored capability polar and non-polar molecules + polar molecules + - + + + + + - + non-polar molecules 13 Alignment of dipoles with E field E + + + + + + + + + + + + + + + - - - - - 14 Polarization Each dipole has its dipole moment, p p Qd C m where Q is the positive one of the two bound charges d is the vector from the negative to the positive charge. nv ptotal pi i 1 where n = number of dipoles per volume. Polarization is dipole moment per unit volume, 1 nv P lim pi v 0 v i 1 C / m2 15 Equivalent polarization The movement of bound charges when induced by an electric field causes changes in surface and volume charge densities. 1. Equivalent polarization surface charge density, s s P a n C / m2 2. Equivalent polarization volume charge density, v an + + + + - + + + + + - + + + + + + - + - + + + + + + - + + + + + + + + - E 16 Electric flux density in a dielectric material (1) D can be calculated from free and bound charges. Net bound charges flowing out of the closed surfaces, Qb P d S C S Let QT Q Qb where QT = total charge Q = free charge + + + - - 17 Electric flux density in a dielectric material (2) QT 0 E d S From s then Q QT Qb (0 E P) d S . s Let D 0 E P we can write Q D dS s where D is an electric flux density in a dielectric material. 18 Equivalent divergence relationships From Qb P a n d S , s use a divergence theorem, we have P d S Pdv. s Since then Qb v dv P v b . We can also show that therefore v 0 E T , D T b v . 19 Electric flux density in dielectric medium (1) If the dielectric material is linear and isotropic, the polarization P is proportional to the electric field E . P 0 e E where e is an electric susceptibility. Then D 0 E e0 E. Let r e 1 where r is a relative permittivity or a dielectric constant. 20 Electric flux density in dielectric medium (2) So we can write D r 0 E or where D E . r 0 F/m. 21 Ex2 A dielectric material has an electric susceptibility e =0.12 and has a uniform electric flux density D = 1.6 nC/m2, determine a) E b) P . c) Average dipole moment if there are 2x1019 dipoles/m3 22 Boundary conditions for dielectric materials: tangential fields It is useful to determine the electric field in a dielectric medium. Dielectric-Dielectric 1 2 and w Dt1 1 Dt 2 2 h Et1 Et1 =Et2 Et2 23 Boundary conditions for dielectric materials: normal fields Dielectric-Dielectric D n1 a21 ( D1 D2 ) S s For a free of charge boundary, D n2 Dn1 = Dn2 and a 21 is the unit vector pointing from medium 2 to medium 1. 1En1 2En2. 24 Use B.C.s to determine magnitude of D and E D n1 q1 1 2 D2 D1 q2 D t1 D n2 D t2 2 D2 D1 cos2 q1 22 sin 2 q1 1 12 E2 E1 sin q1 2 cos2 q1 2 2 25 Ex3 The isotropic dielectric medium with r1 = 3 and r2 = 2 is connected as shown. Given E1 a x 5a y 4a z V/m, determine E 2 and its magnitude, D2 and its magnitude, q1, and q2. Z r13 x-y r22 -Z 26 Boundary conditions for dielectricconductor En Et w dielectric conductor h Dt = Et = 0 Dn = En = s 27 Ex4 Between a dielectric-conductor interface has a surface charge density of s = 2x10-9 C/m2. Given E1 30a x 50a y 70a z V/m, determine E 2 . 28