Download Knowledge Based Systems - Tennessee Tech University

Artificial Intelligence and
Knowledge Based Systems
Fall 2009
Frank Hadlock
Definitions of AI
• The study of representation and search
through which intelligent activity can be
enacted on a mechanical device.
• The study of problems at which human
beings are currently more adept than
computers at solving and the translation
and improvement of human solutions into
forms which can be implemented on a
computer.
Knowledge Based Systems
• Examples
– Expert Systems, Semantic Databases,
Tutoring Systems
• Distinguishing Feature
– Structured so that there is a separation
between knowledge base (rules for inferring
new knowledge), inference engine (applying
rules to existing knowledge), and current
knowledge.
Physical symbol system hypothesis
The physical symbol system hypothesis (PSSH), first
formulated by Newell and Simon in their Turing Award
paper,1 states that “a physical symbol system [such as a
digital computer, for example] has the necessary and
sufficient means for intelligent action.” The hypothesis
implies that computers, when we provide them with the
appropriate symbol-processing programs, will be
capable of intelligent action. It also implies, as Newell
and Simon wrote, that “the symbolic behavior of man
arises because he has the characteristics of a physical
symbol system.”
History
–
–
–
–
–
–
–
Graph theory & state space representation (Euler)
Boolean algebra – propositional calculus (Boole)
Predicate calculus – (Frege)
Descartes Discourse
Turing’s Test
Physical Symbol System Hypothesis
Connectionism
Discourse - Descartes
If there were machines which bore a resemblance to our bodies and imitated
our actions as closely as possible for all practical purposes, we should still have
two very certain means of recognizing that they were not real men. The first is
that they could never use words, or put together signs, as we do in order to
declare our thoughts to others. For we can certainly conceive of a machine so
constructed that it utters words, and even utters words that correspond to bodily
actions causing a change in its organs. … But it is not conceivable that such a
machine should produce different arrangements of words so as to give an
appropriately meaningful answer to whatever is said in its presence, as the
dullest of men can do. Secondly, even though some machines might do some
things as well as we do them, or perhaps even better, they would inevitably fail
in others, which would reveal that they are acting not from understanding, but
only from the disposition of their organs. For whereas reason is a universal
instrument, which can be used in all kinds of situations, these organs need
some particular action; hence it is for all practical purposes impossible for a
machine to have enough different organs to make it act in all the contingencies
of life in the way in which our reason makes us act. (Translation by Robert
Stoothoff)
Turing Test
The Turing test is a proposal for a test of a machine's ability to demonstrate
intelligence. Described by Alan Turing in the 1950 paper "Computing
Machinery and Intelligence," it proceeds as follows: a human judge engages in
a natural language conversation with one human and one machine, each of
which try to appear human; if the judge cannot reliably tell which is which, then
the machine is said to pass the test. In order to test the machine's intelligence
rather than its ability to render words into audio, the conversation is limited to a
text-only channel such as a computer keyboard and screen (Turing originally
suggested a teletype machine, one of the few text-only communication
systems available in 1950).
Knowledge Based Systems
Application Areas
•
•
•
•
•
•
•
•
Game Playing
Automated Reasoning
Expert Systems
Natural Language Understanding
Planning and Robotics
Computer Based Tutoring
Machine Learning
Intelligent Agents
Game Playing and State Space Search
Board games can be represented by a usually large but
finite set of board configurations or states. The squares of
Tic Tac Toe can be numbered 1..9 and each configuration
as a sequence over {H,C,B} where many of the 39 cannot
occur because of order of play. A state BCBBBBBBB may
be followed by any of eight states obtained by replacing
any of the eight Bs by an H. BBBBBBBBB is the initial
state and any state with a row or column or diagonal
consisting of all Cs is a winning state for the Computer. If
the computer can find a path from start to winning state, the
path corresponds to a win for the computer and finding
such a path constitutes an example of artificial intelligence.
State space search
• Represented by a four-tuple
[N,A,S,GD], where:
•N is the problem space
• A is the set of arcs (or links) between
nodes. These correspond to the
operators.
• S is a nonempty subset of N. It
represents the start state(s) of the
problem.
State Space Search continued
• GD is a nonempty subset of N. It
represents the goal state(s) of the
problem. The states in GD are described
using either:
a measurable property of the states
a property of the path developed in the
search (a solution path is a path from
node S to a node in GD )
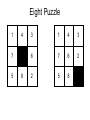
The 8-puzzle problem as state
space search
• states: possible board positions
• operators: one for sliding each square in
each of four directions,
or, better, one for moving the blank square
in each of four directions
• initial state: some given board position
• goal state: some given board position
•Note: the “solution” is not interesting here,
we need the path.
Eight Puzzle
1
4
7
5
8
3
1
4
3
6
7
6
2
2
5
8
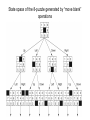
State space of the 8-puzzle generated by “move blank”
operations
Traveling salesperson problem as
state space search
•The salesperson has n cities to visit and
must then return home. Find the shortest
path to travel.
• state space:
• operators:
• initial state:
• goal state:
Automated Reasoning and
Theorem Proving
Logic systems began with Propositional Calculus in which declarative
statements with a truth value of true or false are represented by
P,Q,R, etc and combined with logic operators Or, And, Not, If. A
sentence such as “Bill must take CSC 2020” is represented by letter
P and is true or false. Propositional Calculus was extended to
Predicate Calculus by adding Predicates (relations), variables, and
quantifiers (For All and There Exists). A sentence such as “Every
CS major must take CSC 2020” is represented by “(For All X)(
CSMajor(X)  MustTake( CSC2020 ))” Given some facts
expressed in either Propositional or Predicate Calculus, new facts or
knowledge is inferred by inference rules such as modus ponens or
resolution. If the computer can find a path from given facts to a new
theorem, the path corresponds to a proof and finding such a path
constitutes an example of artificial intelligence
Propositional Logic
• A declarative statement such as “Bill is a CS student”
has a truth value of T or F and is denoted by P (a truth
variable)
• Propositions may be combined with logical operators
and the composite statement has value as shown below.
P  Q is true if either P or Q are true and false if both are false
P  Q is true if both P and Q are true and false if either is false.
¬ P is true if P is false and false if P is true
P  Q is true if P and Q have the same truth value and false if
their values differ
– P  Q is false if P is true and Q is false and true otherwise.
–
–
–
–
• A tautology is always true.
– P  Q  ¬ P  Q is a tautology.
– P  (Q  R)  (P  Q)  (P  R) is a tautology.
Rules of Inference
• P , P  Q then Q - modus ponens
• ¬ Q, P  Q then ¬ P - modus tollens