* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Chapters 5-8 of SOURCEBOOK
Survey
Document related concepts
Quantum chromodynamics wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Renormalization group wikipedia , lookup
Lattice Boltzmann methods wikipedia , lookup
Transcript
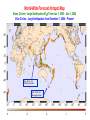
Chapters 5-8 of SOURCEBOOK Spring Semester 2005 Geoffrey Fox Community Grids Laboratory Indiana University 505 N Morton Suite 224 Bloomington IN [email protected] Computational Fluid Dynamics (CFD) in Chapter 5 I • This chapter provides a thorough formulation of CFD with a general discussion of the importance of non-linear terms and most importantly viscosity. • Difficult features like shockwaves and turbulence can be traced to the small coefficient of the highest order derivatives. • Incompressible flow is approached using the spectral element method, which combines the features of finite elements (copes with complex geometries) and highly accurate approximations within each element. • These problems need fast solvers for elliptic equations and there is a detailed discussion of data and matrix structure and the use of iterative conjugate gradient methods. • This is compared with direct solvers using the static condensation method for calculating the solution (stiffness) matrix. Computational Fluid Dynamics (CFD) in Chapter 5 II • The generally important problem of adaptive meshes is described using the successive refinement quad/oct-tree (in two/three dimensions) method. • Compressible flow methods are reviewed and the key problem of coping with the rapid change in field variables at shockwaves is identified. • One uses a lower order approximation near a shock but preserves the most powerful high order spectral methods in the areas where the flow is smooth. • Parallel computing (using space filling curves for decomposition) and adaptive meshes are covered. Hair Combing problem Environment and Energy in Chapter 6 I • This article describes three distinct problem areas – each illustrating important general approaches. • Subsurface flow in porous media is needed in both oil reservoir simulations and environmental pollution studies. – The nearly hyperbolic or parabolic flow equations are characterized by multiple constituents and by very heterogeneous media with possible abrupt discontinuities in the physical domain. – This motivates the use of domain decomposition methods where the full region is divided into blocks which can use different solution methods if necessary. – The blocks must be iteratively reconciled at their boundaries (mortar spaces). – The IPARS code described has been successfully integrated into two powerful problem solving environment: NetSolve described in chapter 14 and DISCOVER (aimed especially at interactive steering) from Rutgers university. Environment and Energy in Chapter 6 II • The discussion of the shallow water problem uses a method involving implicit (in the vertical direction) and explicit (in the horizontal plane) time-marching methods. • It is instructive to see that good parallel performance is obtained by only decomposing in the horizontal directions and keeping the hard to parallelize implicit algorithm sequentially implemented. • The irregular mesh was tackled using space filling curves as also described in chapter 5. • Finally important code coupling (meta-problem in chapter 4 notation) issues are discussed for oil spill simulations where water and chemical transport need to be modeled in a linked fashion • . ADR (Active Data Repository) technology from Maryland is used to link the computations between the water and chemical simulations. Sophisticated filtering is needed to match the output and input needs of the two subsystems. Molecular Quantum Chemistry in Chapter 7 I • This article surveys in detail two capabilities of the NWChem package from Pacific Northwest Laboratory. It surveys other aspects of computational chemistry. • This field makes extensive use of particle dynamics algorithms and some use of partial differential equation solvers. • However characteristic of computational chemistry is the importance of matrix-based methods and these are the focus of this chapter. The matrix is the Hamiltonian (energy) and is typically symmetric positive definite. • In a quantum approach, the eigensystems of this matrix are the equilibrium states of the molecule being studied. This type of problem is characteristic of quantum theoretical methods in physics and chemistry; particle dynamics is used in classical non-quantum regimes. Molecular Quantum Chemistry in Chapter 7 II • NWChem uses a software approach – the Global Array (GA) toolkit, whose programming model lies in between those of HPF and message passing and has been highly successful. • GA exposes locality to the programmer but has a shared memory programming model for accessing data stored in remote processors. • Interestingly in many cases calculating the matrix elements dominates (over solving for eigenfunctions) and this is a pleasing parallel task. • This task requires very careful blocking and staging of the components used to calculate the integrals forming the matrix elements. • In some approaches, parallel matrix multiplication is important in generating the matrices. • The matrices typically are taken as full and very powerful parallel eigensolvers were developed for this problem. • This area of science clearly shows the benefit of linear algebra libraries (see chapter 20) and general performance enhancements like blocking. General Relativity • This field evolves in time complex partial differential equations which have some similarities with the simpler Maxwell equations used in electromagnetics (Sec. 8.6). • Key difficulties are the boundary conditions which are outgoing waves at infinity and the difficult and unique multiple black hole surface conditions internally. • Finite difference and adaptive meshes are the usual approach. Lattice Quantum Chromodynamics (QCD) and Monte Carlo Methods I • Monte Carlo Methods are central to the numerical approaches to many fields (especially in physics and chemistry) and by their nature can take substantial computing resources. • Note that the error in the computation only decreases like the square root of computer time used compared to the power convergence of most differential equation and particle dynamics based methods. • One finds Monte Carlo methods when problems are posed as integral equations and the often-high dimension integrals are solved by Monte Carlo methods using a randomly distributed set of integration points. • Quantum Chromodynamics (QCD) simulations described in this subsection are a classic example of large-scale Monte Carlo simulations which perform excellently on most parallel machines due to modest communication costs and regular structure leading to good node performance. • • • • • From Numerical Integration Lecture: Errors For an integral with N points Monte Carlo has error 1/N0.5 Iterated Trapezoidal has error 1/N2 Iterated Simpson has error 1/N4 Iterated Gaussian is error 1/N2m for our a basic integration scheme with m points • But in d dimensions, for all but Monte Carlo must set up a Grid of N1/d points on a side; that hardly works above N=3 – Monte Carlo error still 1/N0.5 – Simpson error becomes 1/N4/d etc. Monte Carlo Convergence • In homework for N=10,000,000 one finds errors in π of around 10-6 using Simpson’s rule • This is a combination of rounding error (when computer does floating point arithmetic, it is inevitably approximate) and error from formula which is proportional to N-4 • For Monte Carlo, error will be about 1.0/N0.5 • So an error of 10-6 requires N=1012 or • N=1000,000,000,000 (100,000 more than Simpson’s rule) • One doesn’t use Monte Carlo to get such precise results! Lattice Quantum Chromodynamics (QCD) and Monte Carlo Methods II • This application is straightforward to parallelize and very suitable for HPF as the basic data structure is an array. However the work described here uses a portable MPI code. • Section 8.9 describes some new Monte Carlo algorithms but QCD advances typically come from new physics insights allowing more efficient numerical formulations. • This field has generated many special purpose facilities as the lack of significant I/O and CPU intense nature of QCD allows optimized node designs. The work at Columbia and Tsukuba universities is well known. • There are other important irregular geometry Monte Carlo problems and they see many of the same issues such as adaptive load balancing seen in irregular finite element problems. Ocean Modeling • This describes the issues encountered in optimizing a whole earth ocean simulation including realistic geography and proper ocean atmosphere boundaries. • Conjugate gradient solvers and MPI message passing with Fortran 90 are used for the parallel implicit solver for the vertically averaged flow. Tsunami Simulations • These are still very preliminary; an area where much more work could be done Multidisciplinary Simulations • Oceans naturally couple to atmosphere and atmosphere couples to environment including – Deforestration – Emissions from using gasoline (fossil fuels) – Conversely atmosphere makes lakes acid etc. • These are not trivial as very different timescales Earthquake Simulations • Earthquake simulations are a relatively young field and it is not known how far they can go in forecasting large earthquakes. • The field has an increasing amount of real-time sensor data, which needs data assimilation techniques and automatic differentiation tools such as those of chapter 24. • Study of earthquake faults can use finite element techniques or with some approximation, Green’s function approaches, which can use fast multipole methods. • Analysis of observational and simulation data need data mining methods as described in subsection 8.7 and 8.8. • The principal component and hidden Markov classification algorithms currently used in the earthquake field illustrate the diversity in data mining methods when compared to the decision tree methods of section 8.7. World-WideWorld-Wide Forecast Hotspot Map for Likely Locations of Forecast Hotspot Map World-Wide Earthquakes, M > 5, 1965-2000 Great Earthquakes M 7.0 theJan Decade Green Circles = Large Earthquakes M For 7 from 1, 2000 –2000-2010 Dec 1, 2004 Circles: LargeEarthquakes Earthquakes from - Present GreenBlue Circles = Large M December 7 from Jan1,1,2004 2000 – Dec 1, 2004 Dec. 26 M ~ 9.0 Northern Sumatra Dec. 23 M ~ 8.1 Macquarie Island Cosmological Structure Formation (CSF) • CSF is an example of a coupled particle field problem. • Here the universe is viewed as a set of particles which generate a gravitational field obeying Poisson’s equation. • The field then determines the force needed to evolve each particle in time. This structure is also seen in Plasma physics where electrons create an electromagnetic field. • It is hard to generate compatible particle and field decompositions. CSF exhibits large ranges in distance and temporal scale characteristic of the attractive gravitational forces. • Poisson’s equation is solved by fast Fourier transforms and deeply adaptive meshes are generated. • The article describes both MPI and CMFortran (HPF like) implementations. • Further it made use of object oriented techniques (chapter 13) with kernels in F77. Some approaches to this problem class use fast multipole methods. Cosmological Structure Formation (CSF) • There is a lot of structure in universe Computational Electromagnetics (CEM) • This overview summarizes several different approaches to electromagnetic simulations and notes the growing importance of coupling electromagnetics with other disciplines such as aerodynamics and chemical physics. • Parallel computing has been successfully applied to the three major approaches to CEM. • Asymptotic methods use ray tracing as seen in visualization. Frequency domain methods use moment (spectral) expansions that were the earliest uses of large parallel full matrix solvers 10 to 15 years ago; these now have switched to the fast multipole approach. • Finally time-domain methods use finite volume (element) methods with an unstructured mesh. As in general relativity, special attention is needed to get accurate wave solutions at infinity in the time-domain approach. Data mining • Data mining is a broad field with many different applications and algorithms (see also sections 8.4 and 8.8). • This article describes important algorithms used for example in discovering associations between items that were likely to be purchased by the same customer; these associations could occur either in time or because the purchases tended to be in the same shopping basket. • Other data-mining problems discussed include the classification problem tackled by decision trees. • These tree based approaches are parallelized effectively (as they are based on huge transaction databases) with load balance being a difficult issue. Signal and Image Processing • This samples some of the issues from this field, which currently makes surprisingly little use of parallel computing even though good parallel algorithms often exist. • The field has preferred the convenient programming model and interactive feedback of systems like MATLAB and Khoros. • These are problem solving environments as described in chapter 14 of SOURCEBOOK. Monte Carlo Methods and Financial Modeling I • Subsection 8.2 introduces Monte Carlo methods and this subsection describes some very important developments in the generation of “random” numbers. • Quasirandom numbers (QRN’s) are more uniformly distributed than the standard truly random numbers and for certain integrals lead to more rapid convergence. • In particular these methods have been applied to financial modeling where one needs to calculate one or more functions (stock prices, their derivatives or other financial instruments) at some future time by integrating over the possible future values of the underlying variables. • These future values are given by models based on the past behavior of the stock. Monte Carlo Methods and Financial Modeling II • This can be captured in some cases by the volatility or standard deviation of the stock. • The simplest model is perhaps the Black-Scholes equation, which can be derived from a Gaussian stock distribution, combined with an underlying "no-arbitrage" assumption. This asserts that the stock market is always in equilibrium instantaneously and there is no opportunity to make money by exploiting mismatches between buy and sell prices. • In a physics language, the different players in the stock market form a heat bath, which keeps the market in adiabatic equilibrium. • There is a straightforward (to parallelize and implement) binomial method for predicting the probability distributions of financial instruments. However Monte Carlo methods and QRN’s are the most powerful approach. Quasi Real-time Data analysis of Photon Source Experiments • This subsection describes a successful application of computational grids to accelerate the data analysis of an accelerator experiment. It is an example that can be generalized to other cases. • The accelerator (here a photon source at Argonne) data is passed in real-time to a supercomputer where the analysis is performed. Multiple visualization and control stations are also connected to the Grid. Forces Modeling and Simulation • This subsection describes event driven simulations which as discussed in chapter 4 are very common in military applications. • A distributed object approach called HLA (see chapter 13) is being used for modern problems of this class. • Some run in “real-time” with synchronization provided by wall clock and humans and machines in the loop. • Other cases are run in “virtual time” in a more traditional standalone fashion. • This article describes integration of these military standards with Object • Web ideas such as CORBA and .NET from Microsoft. One application simulated the interaction of vehicles with a million mines on a distributed Grid of computers. – This work also parallelized the minefield simulator using threads (chapter 10). Event Driven Simulations • This is a graph based model where independent objects issue events that travel as messages to other objects • Hard to parallelize as no guarantee that event will not arrive from past in simulation time • Often run in “real-time” 1 t1 3 t2 2