Download Chapter 8 - RHIG - Wayne State University

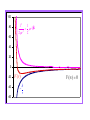
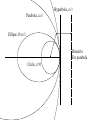
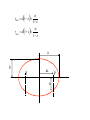
Central-Force Motion
Chapter 8
Prof. Claude A Pruneau
Physics and Astronomy Department
Wayne State University
8.1 Introduction
• Consider motion of two particles affected by a
force connecting the center of the two bodies.
• One of few problems that can be solved
completely.
• Historically important I.e. motion of planets,
alpha-particle scattering on nuclei
8.2 Reduced Mass
• Description of a two-particle system
• Discussion restricted to frictionless
(conservative) systems.
8.2 Reduced Mass (cont’d)
• Assume a force is acting between the two particles along a line
joining them.
• Particle positions described in some arbitrary reference frame
as positions r1 and r2, or in terms of the C.M. frame position, R,
and the relative position vector r= r1 - r2 .
m1
m1
r1
r1
CM
R
r2
Arbitrary Frame
r
CM
R0
r2
m2
m2
CM Frame
Lagrangian for a two-body
system
• Assume the potential energy is only a
function of the distance between the particles,
U=U(r)
• Lagrangian may be written:
2
2
&
L  m1 r&
 U(r)
1  m2 r
2
1
2
1
2
• Translational motion of the system
uninteresting;
– Use R=0.
Two-body CM Coordinates
r
r
m1r1  m2 r2  0
• We have
m2 r
r1 
r
m1  m2
Solving for r1 and r2 :
r r
r  r1  r2
m1 r
r2  
r
m1  m2
Substitute in the Lagrangian r1 and r2 :
2
2
1
&
L  12 m1 r&
 U(r)
1  2 m2 r
2
2
2
m2 r& 1
m1 r&
L  12 m1
r  2 m2
r  U(r)
m1  m2
m1  m2
L  m1
1
2
m1  m2 2
L  12 m1m2
L
m22
m2
r2
r&  12 m2
m1  m2 2
m12
m1  m2 2
r2
r&  12 m1m2
1 m1m2 r&2
r  U(r)
2 m1  m2
r2
r&  U(r)
m1
m1  m2 2
r2
r&  U(r)
r&2
L   r  U(r)
1
2
m1m2

m1  m2
reduced mass
2 to 1 reduction
8.3 Conservation Theorems
• Particle of mass  in a central force field described by
the potential function U(r).
• Symmetry implies conservation of angular
r r
momentum.
L  r  p  constant
Radius vector and momentum lie in a
plane normal to the angular
momentum vector L.
The problem reduced to 2
dimensions: I.e. along “r” and “q”.
L
r
p
• Lagrangian


L  12  r&2  r 2q&2  U(r)
Lagrangian cyclic in q implies:
Angular momentum, pq, conjugate to q, is a
conserved quantity.
L
d L
p&q 
0
q
dt q&
L
2&
pq  & r q  constant
q
First integral of motion
• The system’s symmetry permits the
integration of one equation of motion.
• pq is the first integral of the motion.
• Denote it
l  r q& constant
2
Note
• l can be negative or positive
Interpretation of l as Areal velocity
• The radius vector
sweeps out an area dA
in a time interval dt.
dA  r dq
1
2
r (t1 )
2
rdq
dq
r (t 2 )
The areal velocity is thus
dA 1 2 dq 1 2 &
 2r
 2r q
dt
dt
l

 constant
2
r (t)
Kepler’s 2nd law of planetary motion
dA
 constant
dt
• No particular assumption made about the form of U(r)
implies:
• This result is NOT limited to an inverse-square law
force but is valid for all central forces.
• Since the motion of the CM is not interesting, only
one degree of freedom remains to be considered.
• Linear momentum conservation adds nothing new
here…
• Energy conservation provides the only remaining
equation of motion.
T  U  E  constant
E= 12 v 2  U (r)
E= 12  r&2  r 2q&2  U(r)

Total Energy

2
1
l
E= 12 r&2 
 U (r)
2
2 r
8.4 Equations of Motion
• Assume U(r) is specified. Solve for dr/dt:
1 l2
2
1
E= 2 r& 
 U (r)
2
2 r

Solving for dt, and integrate to get a solution t = t(r).
Invert it to get r = r(t)
Alternatively obtain q= q(r), starting with
dq dt
q&
dq 
dr  dr
dt dr
r&

dr
2
l2
r&

E  U (r)  2 2
dt

r


dr
2
l2
r&

E  U (r)  2 2
dt

r
q (r ) 

dq dt
q&
dq 
dr  dr
dt dr
r&

l  r 2q& constant

 l / r 2 dr

l2 
2   E  U (r ) 
2 r 2 

• Inversion of the result (if possible) yields the standard form
(general) solution r = r(t).
• Because l is constant, dq/dt is a monotonic function of time.
• The above integral is in practice possible only for a limited
number of cases…
Remarks
• with F(r) = rn, solutions may be expressed in
terms of elliptic integrals for certain integers
and fractional values of “n”.
• Solution may be expressed in terms of
circular functions for n=1, -2, and –3.
• Case n = 1 is the harmonic oscillator.
• Case n = -2 is the inverse square law.
Solution using Lagrange equations
Lagrange equation for “r”

L d L

0
r dt &
r

U
2
&
 r&& rq  
 F(r)
r
1
u
r
Use variable change
du
1 dr
1 dr dt
1 r&
 2
 2
 2 &
dq
r dq
r dt dq
r q
Remember
l   r q&
2
l
&
q 2
r
Compute…
l
&
q 2
r
du
1 r&

  2 &  r&
dq
l
r q
d 2u
d    dt d   
 r&&

 r& 
 r&   &
2


dq  l  dq dt  l 
lq
dq
d 2u
 r&&
2 2

  2 r r&&
2
l  l 
dq
l
 r 2 
• Solving
l2
2
d
u
2
r&&  2 u

dq 2
rq&2 
l2

3
u
2


U
2
&
 F(r)
• Substitute back into  r&& rq  
r
d 2  1 1
r 2
  2 F r
2  
dq  r  r
l

• Which is useful if one wishes to find the force
law that produces a particular orbit r=r(q).
Example 8.1 – Log-spiral
Find the force law for a central-force field that allows a particle to
move in a logarithmic spiral orbit given by, r  keaq where k and a
are constants.
d  1
d  eaq  a eaq
Solution:


dq  r  dq  k 
k
Calculate:
2
2  aq
2
d  1 a e

k
dq 2  r 
Now use
r
d 2  1 1
r 2
  2 F r
dq 2  r  r
l

1
1
 r 2   d 2  1  1   r 2   a 2 1 
F r   2   2       2  
 
r
 l   dq  r  r   l   r

To find:
a



l2
  3 a2 1
r
Force is Attractive and Inverse cube!
Example 8.2 – r(t), q(t)
Determine the functions r(t) and q(t) for the problem in Ex 8.1.
Solution:
Start with:
q&
l
l

r 2  k 2 e2aq
Rearrange, integrate:
e
2aq
l
dq 
dt
2
k
Answer:
e
2aq
l
dq   2 dt
k

1  2a lt
q (t) 
ln  2  C 
2a  k

e2aq
lt

 C'
2
2a
k
Similarly for r(t), remember
And write
Answer (2):
l
l

2
r
 k 2 e2aq
r2
2a lt
2aq
e 
C
2
2
k
k
r(t) 
2a lt

 k 2C
Where l and C are determined by the initial conditions
Example 8.3 – Total Energy
What is the total energy of the orbit of the previous two examples?
Solution:
Need U…

U r    Fdr 
l 2




a2 1

l2
1
2
U (r)  
a 1 2
2
r
l
l
&
q  2  2 2aq
r
k e
dr l
l
al
aq
r&
 2 a ke 
2
dq r
r
r

lim U r  0
r
aq
r  ke
dq dq dr
l
&
q

 2
dt dr dt r
dr
 r3
2
1  al 
l
E    

2
2  r 
2r
Given the reference
2


2r 2
lim U r  0
r
 0
l2 a 2  1
8.5 Orbits in a central field
• Radial velocity of a particle in central field


dr
2
l2
r&

E  U (r)  2 2
dt

r
• Vanishes at the roots of the radical


l2
E  U (r)  2 2  0

r
2
l2
E  U (r) 
0
2
2 r
l2
E  U (r) 
0
2
2 r
• Vanishing of dr/dt implies turning points
• Two roots in general: rmin and rmax.
• Motion confined to an annular region between
rmin and rmax.
• Certain combinations of E and l may lead to a
single root: one then has a circular motion,
and dr/dt=0 at all times.
• Periodic motion in U(r) implies the orbit is closed; I.e.
loops on itself after a certain number of excursions
about the center of force.
• The change in q while going from rmin to rmax is a
function of the potential and need not be 180o.
• It can be calculated!
• Because the motion is symmetric in time:
q 

rmax
rmin
 
 l / r 2 dr

l2 
2   E  U (r) 
2 r 2 

• Path closed only if q is a rational fraction of 2p.
• q 2p(a/b) where a and b are integers.
• In this case, after b periods the particle will have
completed a revolutions and returned to its
original position.
• For U (r)  r n1 a closed noncircular path exists
only for n=-2 or +1.
8.6 Centrifugal Energy and Effective Potential
• In dr/dt, dq/dt, …, we have
l2
E  U (r) 
2r 2
• Where each term has the dimension of energy.
• Remember that
• Write
l   r 2q&
l2
1 2 &2
 r q
2
2
2 r
2
l
1 2 &2
• Interpret
 r q
2
2
2 r
l2
Uc 
2 r 2
• The associated force is:
as a “potential energy”
U c
l2
Fc  
 3  rq&2
r
r
• Traditionally called a centrifugal force.
– Although it is, STRICTLY SPEAKING, NOT A FORCE
– but rather a pseudo-force.
– We continue to use the term nonetheless…
• The term l 2 2 r 2
can then be interpreted as the
centrifugal potential energy, and included with U(r) to
define an effective potential energy.
l2
V (r)  U (r) 
2 r 2
• V(r) is fictitious potential that combines the real or
actual potential U(r) with the energy term associated
with the angular motion about the center of force.
• For an inverse-square law central-force motion, one
gets:
k
l2
V (r) 

r
2r 2
100
80
60
l2
1 2&

r q
2
2
2r
40
20
0
-20
-40
-60
V (r)
k

r
V ()  0
Energy
V (r)
Turning point(s)
(apsidal distances)
unbound
r3
r4
E1
1 2
r&
2
r
r1 r2
bound
E2
E3
• Values of E less than Vmin    k 2 2l 2 do not result in
physically real motion; given velocity is imaginary.
• Techniques illustrated here are used in modern atomic,
molecular and nuclear physics (but in the context of QM).
8.7 Planetary Motion – Kepler’s Problem
• Consider the specific case of an inverse-square force
law.
 l / r 2 dr
q (r)  
 constant

k
l2 
2  E  
r 2 r 2 

 
• Integral soluble for with variable substitution u=1/r.
• Define the origin of q so r is a minimum.
cosq 
l2 1
1
k r
2El 2
1
k 2
cosq 
l2 1
1
k r
2El 2
1
k 2
l2
a
k
• Define constants
• Then one can re-write:
2El 2
  1
k
l2 1
2El 2
 1 1 
cosq
2
k r
k
• To get the equation of a conic section with one focus
at the origin
a
r
 1  cosq
a
r
 1  cosq
• The quantity, , is called eccentricity, and
• 2a is termed the latus rectum of the orbit.
• Conic sections are formed by the intersection of a plane and a
cone.
• More specifically … by the loci of points (formed by a plane)
where the ratio of the distance from a fixed point (the focus) to
a fixed line (called the directrix) is a constant.
Hyperbola, >1
Parabola, 1
Ellipse, 0<<1
Directrix
For parabola
Circle, =0
a
r
 1  cosq
q=0 corresponds to a “pericenter”, i.e. rmin whereas rmax corresponds
to the apocenter.
• The general term for turning points is apsides.
• Planetary Motion:
• Major axis
•
a
a
k

1  2 2 E
• Minor axis
b
a
1 
2

l
2 E
 
rmin  a 1  
 
rmax  a 1  
a
1 
a
1 
a
b
P
a
P
a
• Period of elliptic motion:
2
dA
l
T
A
2
 dt  l  dA
0
0
dt 
2
T
A
l
A  p ab
2
2
k

p ab 
p
l
l 2E
• The area of an ellipse is:
• The period is then….
  pk
• Noting

2
E
l
2 E
3/ 2
b  aa
• One also finds:
4p 2  3
 
a
k
2
Kepler’s Third Law
Gm1m2
k
 2
r
• Given the gravitational force:
F(r)  
• The square of the period:
4p 2 a3
4p 2 a3
 

Gm2
G m1  m2
2
r2


• Where the last approx is realized for m1 << m2.
• Kepler’s statement is correct only if the mass m1 of a planet can be
neglected with respect to the mass m2 of the sun.
• Correction needed for Jupiter given that it is 1/1000 of the mass
of the Sun.
Kepler’s Laws
1.
2.
3.
Planets move in elliptical orbits about the sun with
the sun at one focus.
The area per unit time swept out by a radius vector
from the sun to a planet is constant.
The square of a planet’s period is proportional to
the cube of the major axis of the planet’s orbit.
Example 8.4
Halley’s comet, which passed around the sun early in 1986, moves
in a highly elliptical orbit with an eccentricity of 0.967 and a period
of 76 years. Calculate its minimum and maximum distances from
the sun.
1
2 2
Solution: a   Gmsun2 

4p

2



365day 24hr 3600s 
11 Nm
30
  6.67  10
1.99

10
kg
76
yr

yr day hr 
kg 2 


2
4
p



a  2.68  1012 m

We thus find:



m1 0.967  5.27  10
rmin  2.68  1012 m 1 0.967  8.8  1010 m
rmax  2.68  1012
10
m
2







1
2
Basics Facts
• The solar system consists of
– Sun
– Nine planets
– Sixty eight (68) satellites of the planets
– A large number of small bodies
• comets
• Asteroids
– Interplanetary medium.
Inner Solar System
• The inner solar system contains
– Sun
– Mercury
– Venus
– Earth
– Mars:
Outer Solar System
• The planets of the outer solar system
are
– Jupiter,
– Saturn,
– Uranus,
– Neptune,
– Pluto
Some basic facts
Object
Percentage of total mass
Sun
Jupiter
Comets
99.80
0.10
0.05
All other planets
0.04
Satellites and rings
0.00005
Asteroids
0.000002
Cosmic dust
0.0000001
Nine Planets
Nine Planets
Principle Characteristics of the
Planets
Distance
from Sun
(AU)
Revolution
Period
(Years)
Diameter
(km)
Mass
(1023 kg)
Density
(g/cm3)
Mercury
0.39
0.24
4878
3.3
5.4
Venus
Earth
Mars
0.72
1.00
1.52
0.62
1.00
1.88
12102
12756
6787
48.7
59.8
6.4
5.3
5.5
3.9
Jupiter
5.20
11.86
142984
18991
1.3
Saturn
9.54
29.46
120536
5686
0.7
Uranus
19.18
84.07
51118
866
1.2
Neptune
30.06
164.82
49660
1030
1.6
Pluto
39.44
248.60
2200
0.01
2.1
Name
Shoemaker-Levy 9
• A dramatic example
of impact is the
collision of 20 large
pieces of Comet
Shoemaker-Levy 9
with Jupiter in the
summer of 1994.