* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 4. Electric Fields in Matter
Noether's theorem wikipedia , lookup
Casimir effect wikipedia , lookup
Time in physics wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
Speed of gravity wikipedia , lookup
Woodward effect wikipedia , lookup
Electromagnetism wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Mathematical formulation of the Standard Model wikipedia , lookup
Circular dichroism wikipedia , lookup
Lorentz force wikipedia , lookup
Maxwell's equations wikipedia , lookup
Field (physics) wikipedia , lookup
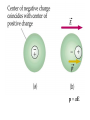
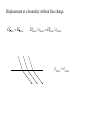
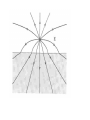
4. Electric Fields in Matter 4.1 Polarization Insulators: All charge is attached to the atoms or molecules. p E Point charge in a homogenously charged sphere p E, 3 ov (v - Volume) Molecules p ||E|| perpE perp Polar molecules have a permanent dipole. F (d )E N pE p E 4.2 The Field of a Polarized Object Polarization P (dipole moment per unit volume) tells how strongly the atoms/molecules are polarized and/or aligned with the electric field. Np P v Take a small volume v that contains, say, N=1000 atoms. Potential generated by the microscopic dipoles: V (r ) 1 40 V rˆ P(r ) r 2 d ' Bound charges V (r) 1 40 S b (r' ) r da' volume charge density surface charge density 1 40 V b (r' ) r d ' b P b P nˆ , where nˆ is the normal on the surface. Example 4.2 Electric field of a uniformly polarized sphere. P Vin z 3 0 Vout rR 1 p rˆ 4o r 2 4 3 p RP 3 constant field rR dipole at the center of the sphere The field inside a dielectric Deriving the expressions for the bound charges we considered pure dipoles. The real dielectric contains physical dipoles. The electric field is much more complicated near the molecular dipoles. The macroscopic field is the average over a small volume that contains many molecules. The average field of the pure and molecular dipoles is the same. 4.3 The Electric Displacement Total charge f b Free charge (at our disposal) f Bound charge (induced, comes along) b Electric displacement (auxiliary field) D 0E P D f D da Q f ,enclosed Boundary conditions Dabove Dbelow f | | But D 0 in general || || || || Dabove Dbelow Pabove Pbelow Example 4.4 Long straight wire with uniform line charge is surrounded by a rubber insulation. Find the electric displacement. 4.4 Linear Dielectrics Most macroscopic fields are weak as compared to the atomic and molecular fields. The polarization is weak. linear dielectric P o eE electric susceptibility e permittivity o (1 e ) permittivity of free space o relative permittivity, dielectric constant r o D E Dielectric constants Table On may calculate D in the same way as E in the vacuum if the different boundary conditions for E and D do not play role. In this case, one simply replaces o This is the case if: a) When the space is filled with a homogenous dielectric. b) When the symmetry of the problem makes D || 0 Charge embedded in a homogenous dielectric material. E 1 q rˆ 2 4 r Bound charges partially screen q. Parallel plate capacitor filled with a dielectric. C A d Qf D rCvacuum dielectric Qf D=0 Dielectrics are used to: a) Increase the capacity b) Keep the plates apart c) Increase the dielectric strength (field strength without a spark) Air: dielectric constant dielectric strength r 1.00059 Ec 3kV / mm Ceramic capacitors r 7 Ec 5.7kV / mm A cut section of a multiplayer capacitor with a ceramic dielectric. Foil wound capacitor. Frequently used dielectrics: r 3.7 Ec 16kV / mm Paper r 5.4 Ec 110 100kV / mm Mica Polysterene r 2.6 Ec 24kV / mm Example 4.5 Metal sphere of radius a carries a charge Q. It is surrounded by a linear dielectric material. Find the potential at the center. Displacement at a boundary without free charge. Dabove Dbelow | | || || Dabove / above Dbelow / below below above 4.4 Boundary Problems with Linear Dielectrics Within a homogenous linear dielectric, Laplace’s equation holds. 2V 0 Boundary conditions on the surface between two dielectrics: Vabove Vbelow Vabove Vbelow above below f n n Example 4.7 A sphere of homogeneous dielectric material is placed into an otherwise uniform electric field. Find the field inside the sphere. Example 4.8 Find the electric field inside and outside the dielectric and the force on the charge. 4.5 Energy in a dielectric system Capacitor For linear dielectrics W 1 CV 2 2 W Cdielectric rCvacuum 1 D Ed 2 Force on a dielectric