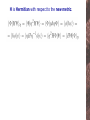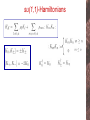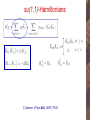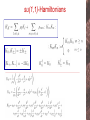* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Non-Hermitian Hamiltonians of Lie algebraic type
Schrödinger equation wikipedia , lookup
Density matrix wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Measurement in quantum mechanics wikipedia , lookup
Coupled cluster wikipedia , lookup
Coherent states wikipedia , lookup
Bra–ket notation wikipedia , lookup
Path integral formulation wikipedia , lookup
Quantum state wikipedia , lookup
Perturbation theory wikipedia , lookup
Self-adjoint operator wikipedia , lookup
Tight binding wikipedia , lookup
BRST quantization wikipedia , lookup
Topological quantum field theory wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Scalar field theory wikipedia , lookup
Compact operator on Hilbert space wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Perturbation theory (quantum mechanics) wikipedia , lookup
Canonical quantization wikipedia , lookup
Canonical quantum gravity wikipedia , lookup
Non-Hermitian Hamiltonians of Lie algebraic type Paulo Eduardo Goncalves de Assis City University London Non Hermitian Hamiltonians Real spectra ? Hermiticity: sufficient but not necessary Non Hermitian Hamiltonians Real spectra ? Hermiticity: sufficient but not necessary - W.Heisenberg, Quantum theory of fields and elementary particles, Rev.Mod.Phys. 29 (1957) 269. J.L.Cardy and R.L.Sugar, Reggeon field theory on a lattice, Phys.rev. D12 (1975) 2514. F.G.Scholtz, H.B.Geyer and F. Hahne, Quasi-Hermitian operators in Quantum Mechanics and the variational principle, Ann. Phys. 213 (1992) 74. T.Hollowood, Solitons in affine Toda field theory, Nucl.Phys. B384 (1992) 523. D.I.Olive, N.Turok, and J.W.R.Underwood, Solitons and the energy momentum tensor for affine Toda theory, Nucl.Phys. B401 (1993) 663. C.M.Bender and S.Boettcher, Real spectra in non-Hermitian Hamiltonians having PT symmetries, Phys.Rev.Lett. 80 (1998) 5243. C.Korff and R.A.Weston, PT Symmetry on the Lattice: The Quantum Group invariant XXZ spin-chain, J.Phys. A40 (2007) 8845. A.K.Das, A.Melikyan and V.O.Rivelles, The S-Matrix of the FaddeevReshetikhin model, diagonalizability and PT-symmetry, J.H.E.P. 09 (2007) 104. When is the spectrum real? • PT-symmetry: Invariance under parity and time-reversal Anti-unitarity: When is the spectrum real? • PT-symmetry: Invariance under parity and time-reversal Anti-unitarity: • Unbroken PT : Not only the Hamiltonian but also the eigenstates are invariant under PT When is the spectrum real? • PT-symmetry: Invariance under parity and time-reversal Anti-unitarity: • Unbroken PT : Not only the Hamiltonian but also the eigenstates are invariant under PT When is the spectrum real? • PT-symmetry: Invariance under parity and time-reversal Anti-unitarity: • Unbroken PT : Not only the Hamiltonian but also the eigenstates are invariant under PT Hermitian Hamiltonian real eigenvalues complex eigenvalues Non-Hermitian Hamiltonian Hermitian Hamiltonian real eigenvalues complex eigenvalues Non-Hermitian Hamiltonian Hermitian Hamiltonian real eigenvalues complex eigenvalues Non-Hermitian Hamiltonian IF Hermitian Hamiltonian real eigenvalues complex eigenvalues Non-Hermitian Hamiltonian IF Isospectral transformation: non-Hermitian Hamiltonian Hermitian counterparts. map Eigenstates of h and H are essentially different: orthogonal basis bi-orthogonal basis Eigenstates of h and H are essentially different: orthogonal basis bi-orthogonal basis Eigenstates of h and H are essentially different: orthogonal basis bi-orthogonal basis bi-orthogonality as non trivial metric Similarity transformation as a change in the metric Pseudo-Hermiticity H is Hermitian with respect to the new metric. H is Hermitian with respect to the new metric. all observables transform H is Hermitian with respect to the new metric. all observables transform non-Hermitian Hamiltonian X ambiguous physics What is being studied? • Non-Hermitian Hamiltonians of Lie algebraic type, P.E.G.Assis and A.Fring, in preparation. • non Hermitian Hamiltonian with real eigenvalues: constraints, metrics, Hermitian counterparts. • eigenvalues and eigenfunctions when possible. What is being studied? • Non-Hermitian Hamiltonians of Lie algebraic type, P.E.G.Assis and A.Fring, in preparation. • non Hermitian Hamiltonian with real eigenvalues: constraints, metrics, Hermitian counterparts. • eigenvalues and eigenfunctions when possible. • Hamiltonians are formulated in terms of Lie algebras. – General approach different models – Successful framework for integrable or solvable models sl2(R)-Hamiltonians sl2(R)-Hamiltonians sl2(R)-Hamiltonians Representation: invariant Quasi-exactly solvable Turbiner et al sl2(R)-Hamiltonians Representation: invariant Quasi-exactly solvable Turbiner et al sl2(R)-Hamiltonians Representation: invariant Quasi-exactly solvable Turbiner et al PT-symmetrize Hermitian conjugates of J’s cannot be written in terms of them su(1,1)-Hamiltonians su(1,1)-Hamiltonians su(1,1)-Hamiltonians C.Quesne, J.Phys A40, (2007) F745. su(1,1)-Hamiltonians C.Quesne, J.Phys A40, (2007) F745. su(1,1)-Hamiltonians C.Quesne, J.Phys A40, (2007) F745. su(1,1)-Hamiltonians Swanson Hamiltonian C.Quesne, J.Phys A40, (2007) F745. D.P.Musumbu, H.B.Geyer, W.D.Heiss, J.Phys A39, (2007) F75. su(1,1)-Hamiltonians Holstein-Primakoff Two-mode su(1,1)-Hamiltonians Hermitian partners • Metric Ansatz: Hermitian partners • Metric Ansatz: constraints Hermitian partners • Metric Ansatz: constraints exact action of the metric on the generators Hermitian partners • Metric Ansatz: constraints exact action of the metric on the generators Recall: Recall: Recall: • Different possible subcases, e.g., purely linear or purely bilinear. Recall: • Different possible subcases, e.g., purely linear or purely bilinear. • Large variety of models may be mapped onto a Hermitian couterpart. Recall: • Different possible subcases, e.g., purely linear or purely bilinear. • Large variety of models may be mapped onto a Hermitian couterpart. • Metric depends either only on momentum or coordinate operators. Reducible Hamiltonian Constraints Reducible Hamiltonian Constraints Appropriate choices lead to the interesting sub cases: Reducible Hamiltonian Constraints Appropriate choices lead to the interesting sub cases: non-negative: µ- = µ-- = µ0- = 0 Reducible Hamiltonian Constraints Appropriate choices lead to the interesting sub cases: non-negative: µ- = µ-- = µ0- = 0 non-positive: µ+ = µ++ = µ+0 = 0 Reducible Hamiltonian Constraints Appropriate choices lead to the interesting sub cases: non-negative: µ- = µ-- = µ0- = 0 purely bilinear: µ+ = µ- = 0 non-positive: µ+ = µ++ = µ+0 = 0 Reducible Hamiltonian Constraints Appropriate choices lead to the interesting sub cases: non-negative: µ- = µ-- = µ0- = 0 non-positive: µ+ = µ++ = µ+0 = 0 purely bilinear: µ+ = µ- = 0 purely linear: µ++ = µ-- = 0 and µ+0 = µ0- = 0 Reducible Hamiltonian Constraints Appropriate choices lead to the interesting sub cases: non-negative: µ- = µ-- = µ0- = 0 non-positive: µ+ = µ++ = µ+0 = 0 purely bilinear: µ+ = µ- = 0 purely linear: µ++ = µ-- = 0 and µ+0 = µ0- = 0 Reducible Hamiltonian Constraints Appropriate choices lead to the interesting sub cases: non-negative: µ- = µ-- = µ0- = 0 non-positive: µ+ = µ++ = µ+0 = 0 purely bilinear: µ+ = µ- = 0 purely linear: µ++ = µ-- = 0 and µ+0 = µ0- = 0 eigenvalues and eigenstates Non-reducible Hamiltonian Constraints Non-reducible Hamiltonian Constraints New solutions for limited sub cases: non-negative: µ- = µ-- = µ0- = 0 non-positive: µ+ = µ++ = µ+0 = 0 Non-reducible Hamiltonian Constraints New solutions for limited sub cases: non-negative: µ- = µ-- = µ0- = 0 non-positive: µ+ = µ++ = µ+0 = 0 purely bilinear: µ+ = µ- = 0 purely linear: µ++ = µ-- = 0 and µ+0 = µ0- = 0 Non-reducible Hamiltonian Constraints New solutions for limited sub cases: non-negative: µ- = µ-- = µ0- = 0 non-positive: µ+ = µ++ = µ+0 = 0 purely bilinear: µ+ = µ- = 0 purely linear: µ++ = µ-- = 0 and µ+0 = µ0- = 0 Eigenstates and Eigenvalues? • So far, we have only calculated metrics and discussed under which conditions non-Hermitian Hamiltonians possess real spectra. Diagonalization Hamiltonian in Harmonic Oscillator form Eigenstates and Eigenvalues? • So far, we have only calculated metrics and discussed under which conditions non-Hermitian Hamiltonians possess real spectra. Diagonalization Hamiltonian in Harmonic Oscillator form Generalized Bogoliubov: New Operators M.S.Swanson, J.Math.Phys 45, (2004) 585. Eigenstates and Eigenvalues? • So far, we have only calculated metrics and discussed under which conditions non-Hermitian Hamiltonians possess real spectra. Diagonalization Hamiltonian in Harmonic Oscillator form Generalized Bogoliubov: New Operators eigenstates and eigenvalues of vacuum M.S.Swanson, J.Math.Phys 45, (2004) 585. Eigenstates and Eigenvalues? • So far, we have only calculated metrics and discussed under which conditions non-Hermitian Hamiltonians possess real spectra. Diagonalization Hamiltonian in Harmonic Oscillator form Generalized Bogoliubov: New Operators eigenstates and eigenvalues of vacuum M.S.Swanson, J.Math.Phys 45, (2004) 585. More constraints for Ñ dependent Hamiltonian More constraints for Ñ dependent Hamiltonian metric-constraints and solvability-constraints combined ? Exact: eigenvalues, eigenstates and suitable metric More constraints for Ñ dependent Hamiltonian metric-constraints and solvability-constraints combined ? Exact: eigenvalues, eigenstates and suitable metric Transition amplitudes Conclusions • Calculated conditions and appropriate metrics with respect to which a large class of non Hermitian Hamiltonians bilinear in su(1,1) generators can be considered Hermitian. • The same non Hermitian Hamiltonians could be diagonalized and it was shown, whithout metrics, that although being non Hermitian real eigenvalues do occur. • Possibility to have complete knowledge of spectra, eigenstates (both of Hermitian and non Hermitian Hamiltonians) and meaningful metrics. • Hamiltonians explored are very general, allowing interesting models as sub cases. • Other algebras may be employed.