Download Fin Heat Transfer Rate

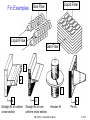
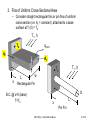
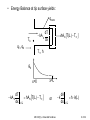
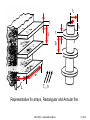
Heat Transfer
Heat Transfer from Extended Surfaces
ME 327(6) – Extended Surfaces
1 of 32
Heat Transfer from Extended Surfaces
1. General Considerations
– Extended Surface refers to a solid material in which energy is
transferred by conduction within its boundaries and by
convection/radiation between its boundaries and the surroundings
– Fins are extended surfaces used primarily to enhance the heat
transfer rate between the solid fins and an adjoining fluid
– For a constant surface temperature Ts , heat transfer rate can be
increased by increasing h or reducing the temperature T of the
surroundings. None of these measures is usually practicable
– Heat transfer rate is usually increased by employing extended
surfaces to increase the heat transfer area by convection
– Fin material should have high k to limit temperature variation from
its base to the tip (want T=Tbase)
T∞, h
T∞, h
A
q = hA (Ts - T∞)
Bare Surface
Ts, A
ME 327(6) – Extended Surfaces
Finned Surface
Ts
2 of 32
Fin Examples
Liquid Flow
Gas Flow
Liquid Flow
Gas Flow
t
w
r
x
x
Straight fin of uniform
cross section
Straight fin of nonuniform cross section
x
Annular fin
ME 327(6) – Extended Surfaces
Pin fin
3 of 32
2. General Conduction Analysis
– Consider the energy balance for a differential area of an
extended surface shown below:
dqconv
qx+dx
qx
x
•
dAs
Ac(x)
dx
Assumptions
•
•
•
•
1-D, S.S, conduction in the x direction with constant k
Radiation from surface negligible or qr = 0
No heat generation or g = 0
h is uniform over the entire surface
ME 327(6) – Extended Surfaces
4 of 32
• Energy Balance yields:
qx  qx  dx  dqconv
where
dqconv  h  dA s  (Ts  T )
Substituting
dT 
dT
d
dT  
 kA c
   kA c
  k   A c
dx   hdA s T  T 
dx 
dx
dx 
dx  
or
d2T  1 dA c  dT  1 h dA s 

(T  T )  0


2  A dx  dx  A k dx  s
dx
 c

 c

• General form of the energy equation for extended
surfaces. Solution is obtained by applying appropriate
B.C.’s to obtain temperature distribution and subsequent
heat flow
ME 327(6) – Extended Surfaces
5 of 32
3. Fins of Uniform Cross-Sectional Area
– Consider straight rectangular fins or pin fins of uniform
cross-section (i.e. Ac = constant ) attached to a base
surface at T (0) = Tb
T∞, h
Tb
qconv
qf
Ac
t
T ∞, h
Tb
x
L
w
Rectangular Fin
B.C. @ x=0 (base)
T=Tb
D
L
x
Pin Fin
ME 327(6) – Extended Surfaces
6 of 32
d2T  1 dA c  dT  1 h dA s 

(T  T )  0


2  A dx  dx  A k dx  s
dx
 c

 c

• Since Ac = constant dA c  0
dx
• Surface area As = P x , where P is the Perimeter
dA
 s P
dx
d2T hP
T  T   0

• Heat equation reduces to:
(1)
2 kA
dx
c
• Assumptions:
– 1-D, S.S. conduction, no energy generation ( g = 0), and
constant Ac
– To simply (1), Define excess temperature as:
d dT

T∞=Constant and
dx dx
( x )  T( x )  T

d2
2

m
0
2
dx
(2)
where
m2 
Sub. into (1)
hP
kA c
General Solution to (2) is ( x )  C1emx  C2e mx
ME 327(6) – Extended Surfaces
7 of 32
•
Hyperbolic functions

1 x
sinh( x )  e  e  x
2

cosh( x ) 
e x  e x
sinh( x )
tanh( x )  x

e  e  x cosh( x )
•

1 x
e  e x
2

See table B-1 is Appendix B
of Text for values of hyperbolic
functions for x = 0 to 10
B.C.’s 1. θ(x=0) = Tb - T∞ = θb
2. at x = L (tip condition)
– This corresponds to any of the following four physical
conditions (Cases A to D):
•
Case (A): Convection heat transfer from the tip.
ME 327(6) – Extended Surfaces
8 of 32
• Energy Balance at tip surface yields:
qconv
 kA c
Tb
qf = qb
hA c T(L )  T 
dT
dx
T ∞, h
θb
x=0
dT
 kA c
 hA c T(L )  T 
dx x L
x=L
or
ME 327(6) – Extended Surfaces
d
k
 h  (L )
dx x L
9 of 32
• From the general solution ( x )  C1emx  C2emx
• At x = 0,
(0)  b  C1e0  C2e0  C1  C2
• At x = L , where h(L)  k
d
dx



h C1emL  C2emL  km C2emL  C1emL
(3)

(4)
• Equations (3) and (4) are then solved to obtain C1 and C2.
C1 and C2 are substituted to obtain the general solution:
 cosh m(L  x )  h mk  sinh m(L  x )

b
cosh mL  h mk  sinh m(L  x )
ME 327(6) – Extended Surfaces
10 of 32
• Total heat energy transferred by fin (qf) may be evaluated
from Fourier’s Law:
d
qf  qb  kA c
dx x 0
• Knowing θ(x), qf is estimated to be:
sinh mL  h mk cosh mL
qf  hPkA c b
cosh mL  h mk  sinh mL
or
qf  M
sinh mL  h mk cosh mL
cosh mL  h mk  sinh mL
where
M  hPkA c b
• And θb is the temperature difference (excess) at the base,
θ b = Tb - T∞
ME 327(6) – Extended Surfaces
11 of 32
• Case (B): Adiabatic condition at the tip (Negligible
Convection at tip)
• Temperature Distribution is:
 cosh m(L  x )

b
cosh mL
qf
qL
x=L
and
x=0
qf  M tanh( mL )
θb
d
0
dx
θL
where
M  hPkA c b
ME 327(6) – Extended Surfaces
12 of 32
• Case (C): Prescribed Temperature at the Tip
• Temperature Distribution is:
 L  sinh(mx )  sinh m(L  x )
  b 

b
sinh(mL )
and
qf  M

cosh mL  L
θb
b
sinh mL
qf
x=L
x=0
θ= θL
where
M  hPkA c b
ME 327(6) – Extended Surfaces
13 of 32
• Case (D): Infinite Fin ( L → ∞, θL → 0)
• Temperature Distribution is:

 e mx
b
L  , (L )  0
T  T
and
qf  M
where
x=0
  T  T  0
θb
M  hPkA c b
ME 327(6) – Extended Surfaces
14 of 32
ME 327(6) – Extended Surfaces
15 of 32
Fin Performance
1. Fin Effectiveness (εf)
εf = ____Fin Heat Transfer Rate____
Heat Transfer Rate Without Fin
f 
•
•
qf
hA c,b b
θb= Tb-T∞
θb
qf
Ac
εf ≥ 0, typically ≥ 2
Etc...
Ac,b is the fin’s cross-sectional area at the base.
In the case of an infinite fin (case D)
1
 2
hPkA c b  kP

f 

 
hA c,b b
hA c,b b
 hA c 
qf
ME 327(6) – Extended Surfaces
16 of 32
1
 2
hPkA C b  kP

f 

 
hA c,b b
hA c,b b
 hA c 
qf
Typical h values
Effectiveness is enhance by:
Process
1. Materials with high k (copper,
aluminum alloys, etc.)
2. High P/A ratios (example: thin, closely
space fins of compact heat
exchangers)
3. Transfer between two fluids: Fins are
used to enhance the heat transfer to
the fluid with the lower h (to give
maximum q). This is usually the gas
side.
For adiabatic tip, 98% of maximum
heat transfer is reached when mL =
2.3
Fin’s Length L ≤ 2.3m
m
h (W / m2 K)
Free Convection
Gases
2 -25
Liquids
50 -1000
Forced Convection
Gases
35 -250
Liquids
50 -20,000
with Phase Change
Boiling or
Condensation
2500 -100,000
hP
kA c
ME 327(6) – Extended Surfaces
17 of 32
2. Fin Resistance (R t,f)
Tb  T
b
qf 

R t,f
R t,f
b
R t,f 
qf
qf
Tb
R t,f
and
b
qb 
Rt,b
q
f  f
qb
T
1
R t,b 
hA c,b
qb
Rt,b
f 
Rt,f
Tb
R t,b 
T
1
hA c,b
• If the fin is to enhance heat transfer, its resistance must not
exceed that of the exposed base.
ME 327(6) – Extended Surfaces
18 of 32
3. Fin Efficiency
q
qf
f  f 
qmax hA f b

qf  b
R t,f
Where Af = surface area of fin
= PL for the straight fin
R t,f 
1
hA f f
qf
Tb
• For the adiabatic tip condition,
f 
M tanh mL
hPL b
where
T
R t,f
M  hPkA c b
or
tanh mL
f 
mL
• For straight fins with active tip (convection at the tip)
tanh mLc
f 
mLc
sinh mL  h mk  cosh mL
Use simple
M
form and Lc   qf  cosh mL  h mk  sinh mL
f
qmax
hPL b
ME 327(6) – Extended Surfaces
19 of 32
1. Rectangular cross-section
P = 2 W when W > t
Af = 2 W Lc
Ap = Profile area = Lc t
w
L
Lc = L + t/2
Lc = corrected fin length with adiabatic tip assumption
– Error due to assumption of adiabatic tip is negligible for
t
2
ht
 0.06
k
– Areas required to calculate heat transfer rate (q) ?
q  hA f f Tb  T 
Need: Af, Lc, Ap
tanh mLc
f 
mLc
1
 2
1
 2
 2h
3
 hP
 Lc 2
 L c  
mL c  
 kA 
 kA c 
 p
– Properties needed to determine the fin efficiency (f) ?
•
Graphs have fin efficiency as a function of:
 h

Lc
 kA 
 p
3
ME 327(6) – Extended Surfaces
1
 2
2
20 of 32
2. Triangular Cross-Section
Af = 2 w [L2 + (t/2)2]1/2
Lc = L
Ap = L t/2
t
2
L
3. Parabolic Cross-Section
Af = 2.05 w [L2 + (t/2)2]1/2
Lc = L
Ap = L t/3
4. Annular Fins

A f  2 r22C  r12
Lc  L  t
2
r2c  r2  t
2
A p  Lc t
w
t
2
r1

t
ME 327(6) – Extended Surfaces
L
r2
L
21 of 32
• 3.18
ME 327(6) – Extended Surfaces
22 of 32
• 3.19
ME 327(6) – Extended Surfaces
23 of 32
Fins With Non-Uniform Cross Sectional Area
• In an annular fin t is constant but the cross sectional area
(2 π r t) varies with r.
• General form of fin equation is:
d2T
1 dT 2h

 T  T   0
2 r dr
kt
dr
where
m2  2h
kt
d2 1 d
2


m
0
2 r dr
dr
or
and
  T  T
• This is the modified Bessel Equation of order zero, with
general solution of the form:
(r )  C1I0 (mr )  C2K 0 (mr )
where
I0 = Modified zero order Bessel function of First kind
K0 = Modified zero order Bessel function of Second kind
ME 327(6) – Extended Surfaces
24 of 32
d
0
• With θ(r1) = θb and adiabatic tip such that
dr r2
C1 and C2 are determined and the temperature distribution
is:
 I0 (mr1)K1(mr2 )  K 0 (mr1)I1(mr2 )

b I0 (mr1)K1(mr2 )  K 0 (mr1)I1(mr2 )
Where
dI0 (mr )
I1(mr ) 
d(mr )
dK 0 (mr )
K1(mr )  
d(mr )
Modified Bessel function of first kind
Modified Bessel function of second kind
• Bessel functions are tabulated in appendix B (text)
ME 327(6) – Extended Surfaces
25 of 32
qf  kA c,b
dT
dr r r1
d
qf  k 2r1t 
dr r r1
K (mr )I (mr )  I (mr )K (mr )
 qf  2kr1tbm 1 1 1 2 1 1 1 2
K 0 (mr1)I1(mr2 )  I0 (mr1)K1(mr2 )
f 

qf
2h r22

 r12 b
R t,f 
1
h  A f  f
Table 3-5 shows the efficiency and surface area for common fin
geometries. Profile area and Volume are also shown.
V  wAp
ME 327(6) – Extended Surfaces
26 of 32
ME 327(6) – Extended Surfaces
27 of 32
ME 327(6) – Extended Surfaces
28 of 32
ME 327(6) – Extended Surfaces
29 of 32
• Actual fin heat transfer rate, qf, could be calculated from
qmax using the expression:
qf  f qmax  f (hA f b )
• Overall Surface Efficiency For Fin Array
qt
qt
o 

qmax hA t b
Where qt  hA b,bare b  NhA f f b = Total heat transfer rate
and
A t  A f  A b,bare = total exposed area
Thus:
NAf
1  f 
o  1 
At
Where N = total number of fins
ME 327(6) – Extended Surfaces
30 of 32
r2
t
r1
t
S
S
w
L
T ∞, h
Representative fin arrays, Rectangular and Annular fins
ME 327(6) – Extended Surfaces
31 of 32
Problem 3.116
ME 327(6) – Extended Surfaces
32 of 32