Download Poynting`s Theorem is the

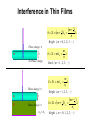
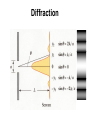
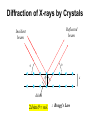
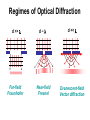
Fundamentals of Photonics
Bahaa E. A. Saleh, Malvin Carl Teich
송석호
Physics Department (Room #36-410)
2220-0923, 010-4546-1923, [email protected]
http://optics.hanyang.ac.kr/~shsong
Course outline
1학기
1. Ray Optics / 4. Fourier Optics (송석호)
3. Beam Optics / 10. Resonator Optics (이광걸)
5. Electromagnetic Optics / 11. Statistical Optics (이진형)
6. Polarization Optics / 19. Acousto-Optics (오차환)
8. Guided-Wave Optics / 9. Fiber Optics (한영근)
2학기
7. Photonic-Crystal Optics / 23. Interconnects/Switches (송석호)
12. Photon Optics / 13. Photons and atoms (이진형)
14. Laser Amplifiers / 15. Lasers (이광걸)
16. Semiconductor Optics / 22. Ultrafast Optics (한영근)
20. Electro-Optics / 21. Nonlinear Optics (오차환)
Course outline
Optics
(Classical)
Ray optics: the behavior of light can be adequately described by rays obeying a set of geometrical rules.
This model of light is called ray optics. From a mathematical perspective, ray optics is the limit of wave optics when
the wavelength is infinitesimally small.
Wave optics: (Scalar) Wave theory in which light is described by a single scalar wavefunction.
Electromagnetic optics: (Vector) Electromagnetic radiation propagates in the form of two mutually coupled
vector waves, an electric-field wave and a magnetic-field wave.
(Quantum)
Quantum optics: Quantum version of electromagnetic theory. Optical phenomena are
characteristically quantum mechanical in nature and cannot be explained classically.
Let’s warm-up
General Physics
Electrodynamics
Question
How does the light propagate through a glass medium?
(1) through the voids inside the material.
(2) through the elastic collision with matter, like as for a sound.
(3) through the secondary waves generated inside the medium.
Secondary
on-going wave
Primary incident wave
Construct the wave front
tangent to the wavelets
What about –r direction?
BASIC EQUATIONS OF ELECTRODYNAMICS in SI units
Maxwell's Equations
Lorentz force law
Auxiliary Fields
Potentials
EM-Wave equations


 


B
E
In vacuum
 E  
  B   0 0
t
t

  
  
  B 
    B  0 0   E  0 0   
t
t  t 
  

2
    B   B





2

 B
 2 B   0 0 2
t 
2


E
 2 E  0 0 2
t

 ˆ  ˆ  ˆ

i
j
k
x
y
z
  
  


    B     B   2 B   2 B
  
  
  
A B  C  A C B  A B C
2B
2B
 0 0 2  0
2
x
t
2E
2E
  0 0 2  0
2
x
t


  
   
Wave equations

Scalar wave equation
 2
 2
 0 0 2  0
2
x
t
   0 cos( kx   t )
k   00  0
2
2

k

1
0 0
vc
Speed of Light
c  2.99792 108 m / sec  3 108 m / s
Transverse Electro-Magnetic (TEM) waves

 
E
  B   0 0
t

 
EB
Electromagnetic
Wave
Energy carried by Electromagnetic Waves
Poynting Vector : Intensity of an electromagnetic wave
 1  
S
EB
(Watt/m2)
0
1
B

  c
S
EB
E

0
1 2 c 2

E 
B
c 0
0
Energy density associated with an Electric field : u E 
1
0 E 2
2
Energy density associated with a Magnetic field : u B 
1 2
B
2 0
Reflection and Refraction
Smooth surface
Rough surface
Reflected ray
n1
n2
Refracted ray
1  1
n1 sin 1  n2 sin  2
Reflection and Refraction
In dielectric media,
c
n( ) 

v ( )
 ( )
0 0
(Material) Dispersion
Interference & Diffraction
Reflection and Interference in Thin Films
• 180 º Phase change
of the reflected light
by a media
with a larger n
• No Phase change
of the reflected light
by a media
with a smaller n
Interference in Thin Films
  2t  m 
1
2

m  12 
 n 

n
Bright ( m = 0, 1, 2, 3, ···)
Phase change: p
n
t
No Phase change
  2t  m n 
m

n
Dark ( m = 1, 2, 3, ···)
  2t  m n1 
Phase change: p
n1
n2
t
Phase change: p
n2 > n1
m

n1
Bright ( m = 1, 2, 3, ···)
1

m

2
  2t  m  12  n 

1
n1
Bright ( m = 0, 1, 2, 3, ···)
Interference
Young’s Double-Slit Experiment
Interference
The path difference
  d sin   m
  r2  r1  d sin 
 Bright fringes m = 0, 1, 2, ····
  d sin   m  12   Dark fringes
The phase difference     2p  2pd sin 


m = 0, 1, 2, ····
Diffraction
Hecht,
Optics,
Chapter 10
Diffraction
Diffraction Grating
Diffraction of X-rays by Crystals
Reflected
beam
Incident
beam



d
dsin
2d sin   m
: Bragg’s Law
Regimes of Optical Diffraction
d >> 
Far-field
Fraunhofer
d~
Near-field
Fresnel
d << 
Evanescent-field
Vector diffraction
Chapter 8. Conservation Laws of EM fields
Electrodynamics, Griffith
8.3 Magnetic Forces Do No Work
8.1 Charge and Energy
8.1.1 Charge conservation (The Continuity Equation)
Let’s begin by reviewing the conservation of charge, because it is the paradigm for all conservation laws.
What precisely does conservation of charge tell us?
If the total charge in some volume changes, then exactly that amount of charge must have passed in
or out through the surface.
This local conservation of charge says
divergence theorem
This is, of course, the continuity equation,
 “the precise mathematical statement of local conservation of charge”.
8.1.2 Poynting's Theorem
In Chapter 2, we found that the work necessary to assemble a static charge distribution
(against the Coulomb repulsion of like charges) is (Eq. 2.45)
Energy of Continuous
Charge Distribution
Likewise, the work required to get currents going (against the back emf) is (Eq. 7.34)
Energy of steady
Current flowing
Therefore, the total energy stored in electromagnetic fields is
 Let’s derive this total energy stored in EM fields more generally
in the context of the energy conservation law for electrodynamics.
 “Energy conservation law for electrodynamics” Poynting Theorem
Energy Conservation and Poynting's Theorem
Suppose we have some charge and current configuration which, at time t, produces fields E and B.
In the next instant, dt, the charges move around a bit.
 How much work, dW, is done by the electromagnetic forces acting on these charges in the interval dt ?
According to the Lorentz force law, the work done on a charge q is
 the work done per unit time, per unit volume, or, the power delivered per unit volume.
Ampere-Maxwell law 
and Faraday's law
 Poynting's theorem
 This is “Work-Energy Theorem" or “Energy Conservation Theorem” of Electrodynamics.
Poynting's Theorem and Poynting Vector
 Poynting's theorem
 Work-Energy Theorem or Energy Conservation Theorem of Electrodynamics.
The first integral on the right is the total energy stored in the fields 
The second term evidently represents the rate at which energy is  carried
out of V, across its boundary surface, by the fields.
Poynting's theorem says
“the work done on the charges by the electromagnetic force is equal to the decrease in
energy stored in the field, less the energy that flowed out through the surface.”
The energy per unit time, per unit area, transported by the fields is called the Poynting vector:
S
1
0
 E  B  (W/m2)  Poynting vector
S  E  H
 Poynting vector in linear media
Poynting's theorem 
 S . da is the energy per unit time crossing the infinitesimal surface da
 the energy flux, if you like (so S is the energy flux density).
Poynting's Theorem and Poynting Vector
The work W done on the charges by the fields will increase their mechanical energy (kinetic, potential, or whatever).
 If we let umech denote the mechanical energy density,
 If we let uem denote the electromagnetic energy density,
U em   uem d
V

 1
1
1
uem    0 E 2  B 2   E  D  H  B
2
0  2


 differential version of Poynting's theorem
 Compare it with the continuity equation, expressing conservation of charge:
 The charge density is replaced by the energy density (mechanical plus electromagnetic),
 the current density is replaced by the Poynting vector.
Therefore, Poynting’s theorem represents the flow of energy
in in exactly the same way that J in the continuity equation describes the flow of charge.
Poynting’s Theorem is the “Work-energy theorem” or “Conservation of Energy”
dU em
dW

  S  ds
S
dt
dt
Work done by the EM field
S
1

 E  B  : Poynting vetor
Energy flowed out through the surface
Total energy stored in the EM field
“The work done on the charges by the electromagnetic force
is equal to the decrease in energy stored in the field,
less the energy that flowed out through the surface” .
dW
d 1
1 2
1
   E  J  dv      0 E 2 
B  dv 
 E  B   ds
dt V
dt V  2
2 0 
0 S
uem
   S  E  J  differential version of Poynting's theorem
t
Poynting’s theorem
uem
   S  E  J
t
S  E H
Let’s prove it directly from Maxwell’s equations
D
B
H
t
t
D
B
  ( E  H )  E  J  E 
H
t
t
B
B
 H  ( E )   H 
t
t
D
D
 H  J 
 E  ( H )  E  J  E 
t
t
E  ( H )  H  ( E )  E  J  E 
 E  
S  E 
S  EH

uem
S  E J  0
t
: Poynting's theorem
For J  0 (in free space),
For a steady state
D
B
H
 E  J
t
t
uem
 0,
t

uem
   S
t
  S  E  J
Poynting’s theorem:
From Ohm’s law,
uem
   S  E  J
t
uem 
E  J  E   E    E 2   J /    J 


1
ED H B , S  EH
2
1

J2
uem
1
   S   E 2    S  J 2 : Poynting's theorem in Ohmic materials
t

I 2 R    S  da
S
 For steady current case
Example. (a) Find the Poynting vector on the surface of a long, straight conducting wire (of radius b and conductivity σ)
that carries a steady current I.
(b) Verify Poynting’s theorem.
I
J
I
, E   az
2
pb

p b 2
I
H  a
on the surface of the wire.
2p b
I2
I2
S  E  H   az  a 


a
r
2p 2b3
2p 2b3
which is directed everywhere into the wire surface.
J  az
To verify Poynting's theorem,
 I2 
 l  2
  S  ds    S  ar ds  
2p bl  I 2 
I R
2 3 
2 
 p b 
 2p b 
S
S
S
Poynting’s vector and Poynting theorem in matter
Problem 8.23 Describe the Poynting’s vector and Poynting theorem for the filed in matter.
 Poynting's theorem in vacuum
The work done on free charges and currents in matter,
 Poynting’s theorem for the fields in matter
 Poynting vector in matter
the rate of change of the electromagnetic energy density
 Electromagnetic energy density in matter
8.2 Momentum of EM fields
8.2.1 Newton's Third Law in Electrodynamics
Consider two charges, q1 and q2, moving with speeds v1 and v2 along the x-axis and y-axis
under magnetic fields B1 and B2.
At an instantaneous time t, each of the forces on q1 and q2, is a sum of electric and magnetic forces:
Fq 1,2  Fe  Fm
Fq1  Fq2
Fq1  Fq2
 If yes, Newton's third law can also valid
in electrodynamics
 If not, Newton's third law looks not to be valid
in electrodynamics
 However, the third law must be hold ALL THE TIME!
 If not, therefore, there must be another force hidden elsewhere.
 We will see that the fields themselves carry forces (or, momentum)
 Only when the field momentum is added to the mechanical momentum of
the charges, momentum conservation (or, the third law) is restored.
Newton's Third Law in Electrodynamics
Imagine a point charge q traveling in along the x-axis at a constant speed v.
q
 Because it is moving, its electric field is not given by Coulomb's law.
Nevertheless, E still points radially outward from the instantaneous position
of the charge.
(In Chapter 10)
If the velocity and acceleration are both zero,
Generalized Coulomb field (velocity field)
Radiation field (acceleration field)
Since, moreover, a moving point charge does not constitute a steady current,
 its magnetic field is not given by the Biot-Savart law.
 Nevertheless, it's a fact that B still circles around the axis.
q
 Therefore, at an instantaneous time t, a situation with moving point charges
at constant velocities may be regarded as an electromagnetostatic case.
Newton's Third Law in Electrodynamics
Now suppose two identical charges, q1 and q2,
moving with a same speed along the x and y axes.
( This is an electromagnetostatic case at an instantaneous time t.)
 The electrostatic force between them is equal in magnitude
but repulsive in direction:
Fe ,q2  Fe ,q1
 How about the magnetic force?
 The magnetic field B1 generated by q1 points into the page (at the position of q2),
so the magnetic force on q2 is toward the right.
 The magnetic field B2 generated by q2 points out of the page (at the position of q1),
so the magnetic force on q1 is upward.
Fm,q2  Fm,q1
The electromagnetic force of q1 on q2 is equal, but not opposite to the force of q1 and q2.
 The result may reveal violation of Newton’s third law in electrodynamics!
In electrostatics and magnetostatics the third law holds, but in electrodynamics it does not.
Is it true?
 The third law must be hold ALL THE TIME!
 From the third law, we know that the proof of momentum conservation rests on the
cancellation of internal forces:   Fi  dP/dt  0 
Therefore, let’s prove the momentum conservation in electrodynamics!
 The fields themselves carry momentum.
 Only when the field momentum is added to the mechanical momentum of the charges,
momentum conservation (or, the third law) is restored.
Fq1  Fq2
8.2.2 Maxwell’s Stress Tensor for Field Momentum
Now we know that the fields themselves must carry momentum.
To find out the field momentum, let’s calculate the total EM force on the charges in volume V
in terms of Poynting vector S and stress tensor T:
EM force 
The force per unit volume is
A term seems to be "missing" from the symmetry in E and B, which can be achieved by inserting (∇ • B)B (= 0)
Using the vector calculus identity of
It can be simplified by introducing the Maxwell stress tensor T
Maxwell’s stress tensor
 It can be written more compactly by introducing the Maxwell stress tensor.
Maxwell’s stress tensor:
, and so on.
The divergence of it has an its j-th component,
Thus the force per unit volume can be written in the much simpler form:
The total EM force on the charges in volume V is therefore
* In static case 

*T
ij
 The force per unit area (or, stress) on the surface  called by “Stress Tensor”
8.2.3 Conservation of momentum for EM fields
According to the second law, the force on an object is equal to the rate of change of its momentum:
( Pmech is the mechanical momentum of the particles contained in the volume V.)
: Conservation of momentum in electromagnetics
(Poynting theorem for energy conservation)
uem
(In first integral)
(In first integral)
 Momentum stored
in the EM fields
g  0 0S   0  E  B   Momentum density
in the EM fields
(In second integral)
U em   uem d
V
 Energy stored
in the EM fields

1
1
uem    0 E 2  B 2   Energy density
2
0  in the EM fields
(In second integral)
 Momentum flux density
(Momentum per unit time, per unit area)
S
1
0
E  B
 Energy flux density
(Energy per unit time, per unit area)
 Momentum flux
 Energy flux
(Momentum per unit time passing through da)
(Energy per unit time passing through da)
Conservation of momentum for EM fields
 Total momentum stored in EM fields
g  0 0S

 Pmech  g     T
dt
(In differential form)
 Momentum density stored in EM fields
 Total momentum per unit time passing through a closed surface
 Momentum flux density
(Momentum per unit time, per unit area)
 T  0
If V is all of space, no momentum flows in and out 

 Pmech  P   constant
 Total (mech + EM) momentum is conserved.
If the mechanical momentum in V is not changing
(for example, in a region of empty space)
g
   T
t
 

g
 Pmech   0  V   d   S T  da  V   T d
dt
 t 
 g    T : Continuity equation of EM momentum
t



    J 
t
 T playing the part of J  Local conservation of filed momentum

Conservation of Energy and Momentum for EM fields
Momentum Conservation
Energy Conservation
uem

 umech  uem     S
dt
uem
 
V

1
1
   0 E 2  B2 
2
0 
Poynting Vector S

 Pmech  Pem     T
dt
Pem    0 0S  d    0  E  B  d
V
g   0 0S   0  E  B 
S : Energy per unit area (Energy flux density), per unit time transport by EM fields
00S : Momentum per unit volume (Momentum density) stored in EM fields
Stress Tensor
T
T
T
: EM field stress (Force per unit area) acting on a surface
: Flow of momentum (momentum per unit area, unit time) carried by EM fields
Continuity Equations of EM fields in empty space
uem
    S 
S  playing the part

t

    J 
t
g
   T
T playing the part
t
   
of J  Local conservation of field energy
of J  Local conservation of field momentum
8.2.4 Angular Momentum
Energy density and Momentum density of Electromagnetic fields
g   0 0S   0  E  B 
Density of angular momentum of electromagnetic fields
em
Example 8.4
 r  g   0 r   E  B  
Two long charged cylindrical shells of length l are coaxial with a solenoid carrying current I.
When the current in the solenoid is gradually reduced, the cylinders begin to rotate.
Where does the angular momentum of the cylinder comes from?
Before the current was switched off, there were an electric field and a magnetic field:
g
em
 r  g   0 r   E  B   
current I
g
 constant over the volume of
Total angular momentum in the fields (before switching off):
Example 8.4 (continued)
When the current is turned off,
the changing magnetic field induces a circumferential electric field, given by Faraday's law:
Torque on the outer cylinder:
 Angular momentum of the outer cylinder:
Torque on the inner cylinder:
 Angular momentum of the inner cylinder:
Total angular momentum of the inner and outer cylinders:
Which is the same as the angular momentum of the field:
 The total angular momentum (fields plus matter) is conserved.
Therefore, the angular momentum lost by fields is precisely equal
to the angular momentum gained by the cylinders.
current I
8.3 Magnetic Forces Do No Work
(5.1.2) The magnetic force in a charge Q, moving with velocity v in a magnetic field B, is
 Magnetic forces do no work!
 Magnetic forces may alter the direction in which a particle moves,
but they cannot speed it up or slow it down.
Poynting’s vector and Poynting theorem in matter
Problem 8.23 (a) Describe the Poynting’s vector and Poynting theorem for the filed in matter.
 Poynting's theorem in vacuum
The work done on free charges and currents in matter,
 Poynting’s theorem for the fields in matter
S  E H
 Poynting vector in matter
the rate of change of the electromagnetic energy density
 Electromagnetic energy density in matter
EM force and momentum density in matter
Problem 8.23 (b) Describe the force density and Momentum density for the filed in matter.
The force per unit volume :
The momentum density :
g   0 0S   0  E  B 
In matter,
f  T 

D B
t
g  D  B  S
 EM force per unit volume in matter
 EM momentum density in matter
Chapter 9. Electromagnetic waves
Electrodynamics, Griffith
9.1 Waves in One Dimension
9.1.1 The Wave Equation
 It represents a wave of fixed shape
traveling in the +z direction at speed v.
 (Classical or Mechanical) Wave Equation = Equation of Motion
 Therefore, the Wave Equation admits as solutions all functions of the form
9.1.2 Sinusoidal Waves
(i) Terminology:
Of all possible wave forms, the sinusoidal one is
(At time t = 0)
(At z = 0)
A is the amplitude of the wave
 it is positive, and represents the maximum displacement from equilibrium.
The argument of the cosine,  = k(z-vt) + , is called the phase
  is the phase constant
 Obviously, you can add any integer multiple of 2p to  without changing f (z, t)
 Ordinarily, one uses a value in the range 0 ≤  ≤ 2p
k is the wave number
 it is related to the wavelength  by the equation 
One full cycle in a time period 
 = kvT = 2p 
Frequency v (number of oscillations per unit time) 
Angular frequency , the number of radians swept out per unit time 
 A sinusoidal waves in terms of k and 
Sinusoidal Waves
(ii) Complex notation
In view of Euler's formula,
Complex wave function:
 Complex amplitude
 The actual wave function is the real part:
 The advantage of the complex notation is that exponentials are much easier
to manipulate than sines and cosines.
(iii) Linear combinations of sinusoidal waves
Any wave can be expressed as a linear combination of sinusoidal ones:
(Fourier transformation)
 k includes negative values
 This does not mean that  and  are negative: wavelength and frequency are always
positive.
 k to run through negative values in order to represent waves going in both directions.
Note the point that any wave can be written as a linear combination of sinusoidal waves,
 therefore if you know how sinusoidal waves behave, you know in principle how any wave behaves.
 So from now on, we shall confine our attention to sinusoidal waves.
9.1.3 Boundary conditions: Reflection and Transmission
 The incident wave
 The reflected wave
The transmitted wave 
All parts of the system are oscillating at the same frequency 
(a frequency determined by the person who is shaking the string)
Since the wave velocities are different in the two strings,
 the wavelengths and wave numbers are also different:
For a sinusoidal incident wave, then, the net disturbance of the string is:
Boundary conditions: Reflection and Transmission
At the join (z = 0),
the displacement and slope just slightly to the left (z = 0-) must equal those slightly to the right (z = 0+),
or else there would be a break between the two strings.
The real amplitudes and phases, then, are related by
 all three waves have the same phase angle
If the second string is lighter than the first,
If the second string is heavier than the first,
 the reflected wave is out of phase by 180o
In particular, if the second string is infinitely massive,
9.1.4 Polarization
Transverse Waves: the displacement is perpendicular to the direction of propagation
Longitudinal Waves: the displacement is along the direction of propagation
Transverse waves occur in two independent states of polarization 
Vertical polarization:
Horizontal polarization:
Any other Polarization:
Polarization Vector:
Any transverse wave can be considered a superposition of two waves: one horizontally polarized, the other vertically:
9.2 Electromagnetic waves in Vacuum
9.2.1 The Wave Equation for E and B
In Vacuum, no free charges and no currents 
E  0
B  0
E  
B
t
  0, J  0, q  0, I  0
  B  0 0
Let’s derive the wave equation for E and B from the curl equations.
Each Cartesian component of E and B satisfies
Notice the crucial role played by Maxwell's contribution to Ampere's law
 Without it, the wave equation would not emerge,
 there would be no electromagnetic theory of light.
E
t
9.2.2 Monochromatic Plane Waves
Sinusoidal waves with a frequency  are called monochromatic.
Sinusoidal waves traveling in the z direction and have no x or y dependence, are called plane waves,
because the fields are uniform over every plane perpendicular to the direction of propagation.
Monochromatic Plane Waves
Monochromatic Plane Waves
 Electromagnetic waves are transverse:
 the electric and magnetic fields are perpendicular to the direction of propagation
Evidently, E and B are in phase and mutually perpendicular;
their (real) amplitudes are related by 
Example 9.2
If E points in the x direction, then B points in the y direction,
Or, taking the real part,
The monochromatic plane wave as a whole is said to be polarized in the x direction
(by convention, we use the direction of E to specify the polarization of an electromagnetic wave).
Monochromatic Plane Waves
We can easily generalize to monochromatic plane waves traveling in an arbitrary direction.
k  propagation (or wave) vector, pointing in the direction of propagation,
whose magnitude is the wave number k.
Because E is transverse 
The actual (real) electric and magnetic fields in a monochromatic
plane wave with propagation vector k and polarization n are
9.2.3 Energy and Momentum in Electromagnetic Waves
Energy per unit volume stored in electromagnetic fields 
In the case of a monochromatic plane wave,
 Electric and magnetic contributions are equal
Energy flux density (energy per unit area, per unit time; Poynting vector)
For monochromatic plane waves propagating in the z direction,
g   0 0S 
Momentum density stored in the fields 
For monochromatic plane waves 
g
1
S
c2
1
S
c2
Intensity (time average power per unit area transported by an electromagnetic wave)
)
g 
9.3 Electromagnetic waves in Matter
9.3.1 Propagation in Linear Media
In linear and homogeneous media with no free charge and no free current,
E  0
B  0
E  -
B
t
  B  
E
t
(For most materials,  is very close to 0)
Boundary conditions
I  Saverage  S
9.3.2 Reflection and Transmission at Normal Incidence
Suppose xy plane forms the boundary
between two linear media.
Incident wave
A plane wave of frequency ω is
traveling in the z direction (from left),
polarized along x direction (TM polarization).
Transmitted wave
Reflected wave
Incident wave
E I ( z, t )  E0 I exp  i  k1 z  t   x
B I ( z, t ) 
1
E0 I exp  i  k1 z  t   y
v1
Reflected wave
E R ( z, t )  E0 R exp  i  k1 z  t   x
B R ( z, t )  
1
E0 R exp  i  k1 z  t   y
v1
Transmitted wave
E T ( z, t )  E0T exp  i  k2 z  t   x
BT ( z , t ) 
1
E0T exp  i  k2 z  t   y
v2
Reflection and Transmission at Normal Incidence
At z = 0,
The real amplitudes are related by
R+T=1
9.3.3 Reflection and Transmission at Oblique Incidence
x
All three waves have the same frequency .
Transmitted wave
The incident, reflected, and transmitted wave
vectors form a plane (called the plane of incidence),
Because the boundary conditions must hold
at all points on the plane, and for all times,
the exponential factors must be equal at z = 0 plane.
Incident wave
Reflected wave
 Phase Matching Condition
if y = 0
Transmitted wave
(Snell's law)
Fresnel’s Equations
Suppose that the polarization of the incident wave is parallel to the plane of incidence – Transverse Magnetic (TM) polarization
(Boundary Conditions)
(0 = 0) since no z-component,
(iii) 
(iv) 
Fresnel’s Equations
Fresnel’s Equations
(TM polarization: B is perpendicular to the plane of incidence)
(For TM polarization)



The transmitted wave is always in phase with the incident one
The reflected wave is in phase ("right side up"), if a > b,
The reflected wave is 180o out of phase ("upside down") if a < b.
The amplitudes of the transmitted and reflected waves depend on the angle of incidence.
 because a is a function of I :
Interestingly, there is all intermediate angle, B (called Brewster's angle)
The reflected wave is completely extinguished when a = b :
 For the typical case
The power per unit area striking the interface is
Fresnel’s Equations
(TE polarization: E is perpendicular to the plane of incidence)
For the case of polarization perpendicular to the plane of incidence (TE polarizion)
(i.e. electric fields in the y direction)
(For TE polarization)
 The transmitted wave is always in phase with the incident one.
 The reflected wave is in phase ("right side up"), if ab < 1,
 The reflected wave is 180o out of phase ("upside down") if a b > 1.
Is there a Brewster’s angle for TE polarization?
 E0R = 0 would mean that ab = 1,
No Brewster angle
9.4 Absorption and Dispersion
Looks strange!
9.4.1 Electromagnetic waves in Conductors
According to Ohm's law, the (free) current density is proportional to the electric field:
Maxwell' s equations for linear media with no free charge assume the form,
Plane-wave solutions are
complex wave number
The imaginary part, k , results in an attenuation of the wave
(decreasing amplitude with increasing z):
 skin depth
Determine the relative amplitudes, phases, and E and B in conductors
For E field polarized along the x direction,
Let’s express the complex wave number in terms of its modulus and phase
(Phase)
E and B fields are no longer in phase
 B field lags behind E field.
(Amplitude)
~ e k z
The (real) electric and magnetic fields are, finally,

Energy density and intensity in conductors
Problem 9.21
(a) Calculate the (time averaged) energy density of an electromagnetic plane wave in a conducting medium.
Show that the magnetic contribution always dominates.
(b) Show that the intensity is
The ratio of the magnetic contribution to the electric contribution is
The average of the product of the cosines is
Wave Equation in Frequency Domain = Helmholtz Equation
 (r , t )
 2 (r , t )
  (r , t )  
 
0
2
t
t
2
 Wave equation in space-domain
Let us consider the Fourier transform of the electromagnetic field:
(Fourier transform)
(Inverse Fourier transform)
 (r , t )
 2 (r , t )
  (r , t )  
 

t
t 2
2

2

 k 2  (r, )  0
k  k  jk    1  j
 Wave equation in frequency domain = Helmholtz Equation


Frequency-domain Maxwell equations in a source-free space
Using the temporal inverse Fourier transform, for instance, of E field,
H  J 
D
t
By similar reasoning, finally we can have the Maxwell’s equations in frequency domain:
  H(r, )  J(r, )  j D(r, )
  E(r, )   jB(r, )



j



 t

  D(r, )   (r, )
  J(r, )   j (r, )
  B(r, )  0
 The frequency-domain equations involve one fewer derivative
(the time derivative has been replaced by multiplication by jω), hence may be easier to solve.
 However, the inverse transform may be difficult to compute.
9.4.2 Reflection at a Conducting Surface
The general boundary conditions for electrodynamics;
(f : the free surface charge)
(Kf : the free surface current)
Consider a monochromatic plane wave, traveling in z, polarized in x (TM), approaches from the left,
Will be attenuated as it penetrates into the conductor
For a perfect conductor
 The wave is totally reflected, with a 180o phase shift.
9.4.3 Frequency dependence of permittivity in dielectric media
The electrons in a dielectric are bounded to specific molecules.
Fnet  Fbinding  Fdamping  Fdriving
d 2x
m 2
dt
Dipole moment 
If there are N molecules per unit volume
: complex permittivity
: Absorption coefficient
: Refractive index
Frequency dependence of permittivity (Dispersion)
: complex permittivity
: Absorption coefficient
: Refractive index
 n is a function of frequency (wavelength)
A prism spreads white light out into a rainbow of colors.
 This phenomenon is called dispersion.
(A typical glass)
The speed of a wave depends on its frequency,
 The supporting medium is called dispersive.
Wave velocity
(Phase velocity) 
Group velocity 
The energy carried by a wave packet in a dispersive medium ordinarily travels at the group
velocity,
not the phase velocity.
Phase Velocity and Group Velocity
Phase velocity 
Group velocity 
Problem 9.23 In quantum mechanics, a free particle of mass m traveling in the x direction is described by the wave function
Calculate the group velocity and the phase velocity.
Which one corresponds to the classical speed of the particle?
 Note that the phase (wave) velocity is half the group velocity.
9.4.3 Frequency dependence of permittivity in dielectric media
If you agree to stay away from the resonances,
the damping g can be ignored.
 Cauchy's formula
anomalous dispersion
Anomalous Dispersion
Problem 9.25 Find the width of the anomalous dispersion region for the case of a single resonance at frequency 0
for the case of a single
resonance at frequency 0
At the extreme points in frequencies, 1 and 2,
anomalous dispersion
 The width of the anomalous region:
The index of refraction assumes its maximum and minimum values at points
where the absorption coefficient is at half-maximum.
 The full-width at half maximum (FWHM) of the absorption coefficient is g 