Download Learning Classifier Systems - Operations, Information and Decisions

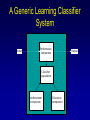
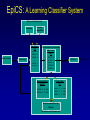
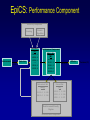
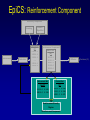
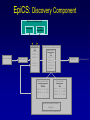
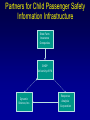
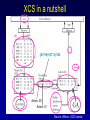
Evolutionary Computation
Genetic Algorithms
Genetic Programming
Learning Classifier Systems
Genetic Algorithms
• Population-based technique for discovery
of knowledge structures
• Based on idea that evolution represents
search for optimum solution set
• Massively parallel
The Vocabulary of GAs
• Population
– Set of individuals, each represented by one or
more strings of characters
• Chromosome
– The string representing an individual
The vocabulary of GAs, contd.
• Gene
– The basic informational unit on a chromosome
• Allele
– The value of a specific gene
• Locus
– The ordinal place on a chromosome where a
specific gene is found
Thus...
Chromosome
011010
Gene
(Allele="0")
Locus=5
Genetic operators
• Reproduction
– Increase representations of strong
individuals
• Crossover
– Explore the search space
• Mutation
– Recapture “lost” genes due to crossover
Genetic operators illustrated...
Parent 1:
Parent 2:
Parent 1:
Parent 2:
Parent 1:
Parent 2:
011010
000110
011010
000110
011010
000110
Simple reproduction
Offspring 1:
Offspring 2:
Reproduction with
crossover at locus 3
Simple reproduction with mutation
at locus 3 for offspring 1
011010
000110
Offspring
1:
Offspring
2:
011110
000010
Offspring 1:
010010
000110
Offspring 2:
GAs rely on the concept of
“fitness”
• Ability of an individual to survive into the
next generation
• “Survival of the fittest”
• Usually calculated in terms of an objective
fitness function
– Maximization
– Minimization
– Other functions
Genetic Programming
• Based on adaptation and evolution
• Structures undergoing adaptation are
computer programs of varying size and
shape
• Computer programs are genetically “bred”
over time
The Learning Classifier System
• Rule-based knowledge discovery and
concept learning tool
• Operates by means of evaluation, credit
assignment, and discovery applied to a
population of “chromosomes” (rules)
each with a corresponding “phenotype”
(outcome)
Components of a
Learning Classifier System
• Performance
– Provides interaction between environment and
rule base
– Performs matching function
• Reinforcement
– Rewards accurate classifiers
– Punishes inaccurate classifiers
• Discovery
– Uses the genetic algorithm to search for plausible
rules
The Learning Classifier System
• Rule-based knowledge discovery and
concept learning tool
• EpiCS
– First Learning Classifier System designed
for use in epidemiologic surveillance
– Supervised learning environment
Knowledge Representation
• Classifiers
– IF-THEN rules
• Condition=“genotype”
• Action=“phenotype”
– Strength metric
– Encoded as bit strings or numerics
• Population
– Fixed size collection of classifiers
Low-level knowledge representation:
The Classifier
0111*00011*111:0
Taxon
34.9
Action Bit
Strength
• Taxon is analogous to a condition (LHS) of an
IF-THEN rule
• Action bit is analogous to an action (RHS) of an
IF-THEN rule
• Strength is an internal fitness function
High-level knowledge representation:
Macrostate Population
Number
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Classifier
****0**********:0
****1**********:1
****0*********0:0
****1*********0:1
****1********1*:1
****0********1*:0
****0*0********:0
****1**********:0
***00**********:0
0***0**********:0
****0*****1****:0
*0**0**********:0
**1*1**********:1
**1*1*********0:1
***00*********0:0
****1**0*******:1
****10*********:1
****1*********0:0
Proportional
Strength
0.39958000
0.38533600
0.08509200
0.08131500
0.02613600
0.00721500
0.00503500
0.00139700
0.00103500
0.00103400
0.00103100
0.00100800
0.00094900
0.00085500
0.00085000
0.00084300
0.00065600
0.00063200
N
380
382
94
91
28
8
5
2
1
1
1
1
1
1
1
1
1
1
Components of a
learning classifier system
• Performance
– Provides interaction between environment and
classifier population
– Performs matching function
• Reinforcement
– Rewards accurate classifiers
– Punishes inaccurate classifiers
• Discovery
– Uses the genetic algorithm to search for plausible
knowledge structures
Generic
Machine Learning Model
Input
Performer
Knowledge Base
Learner
Critic
Output
A Generic Learning Classifier
System
Input
Performance
component
Output
Classifier
population
Reinforcement
component
Discovery
component
EpiCS: A Learning Classifier System
Discovery Component
Covering
Environment
Detectors
10010
Genetic
Algorithm
Population
[P]
01001:1
10010:0
1*010:1
--**110:1
1*001:0
Performance Component
Match Set
[M]
10**0:1
1**1*:1
1001*:1
***10:0
100*0:0
Not-correct Set
Not[C]
***10:0
100*0:0
0.560
0.334
1001*:1
Correct Set
[C]
10**0:1
1**1*:1
1001*:1
Reinforcement/Penalty
Regime
Reinforcement Component
0.560
0.334
0.871
Effector
Decision (=1)
EpiCS: Performance Component
Discovery Component
Covering
Environment
Detectors
10010
Genetic
Algorithm
Population
[P]
01001:1
10010:0
1*010:1
--**110:1
1*001:0
Performance Component
Match Set
[M]
10**0:1
1**1*:1
1001*:1
***10:0
100*0:0
Not-correct Set
Not[C]
***10:0
100*0:0
0.560
0.334
1001*:1
Correct Set
[C]
10**0:1
1**1*:1
1001*:1
Reinforcement/Penalty
Regime
Reinforcement Component
0.560
0.334
0.871
Effector
Decision (=1)
Performance component
• Creates a subset (the matchset, [M]) of all
classifiers in population [P] whose conditions
match a string received from the environment
• From [M], a single classifier is selected, based
on its strength as a proportion of the sum of
all strengths in [M]
• The action of this classifier is then used as the
output of the system
EpiCS: Reinforcement Component
Discovery Component
Covering
Environment
Detectors
10010
Genetic
Algorithm
Population
[P]
01001:1
10010:0
1*010:1
--**110:1
1*001:0
Performance Component
Match Set
[M]
10**0:1
1**1*:1
1001*:1
***10:0
100*0:0
Not-correct Set
Not[C]
***10:0
100*0:0
0.560
0.334
1001*:1
Correct Set
[C]
10**0:1
1**1*:1
1001*:1
Reinforcement/Penalty
Regime
Reinforcement Component
0.560
0.334
0.871
Effector
Decision (=1)
Reinforcement component
• Correct set [C] is created from classifiers in [M]
advocating correct decisions
• Remaining classifiers in [M] form Not[C]
• Tax is deducted from the strengths of all
classifiers in [C]
• Reward is added to the strengths of all
classifiers in [C], biased for generality
• Penalty is deducted from the strengths of all
classifiers in Not[C]
EpiCS: Discovery Component
Discovery Component
Covering
Environment
Detectors
10010
Genetic
Algorithm
Population
[P]
01001:1
10010:0
1*010:1
--**110:1
1*001:0
Performance Component
Match Set
[M]
10**0:1
1**1*:1
1001*:1
***10:0
100*0:0
Not-correct Set
Not[C]
***10:0
100*0:0
0.560
0.334
1001*:1
Correct Set
[C]
10**0:1
1**1*:1
1001*:1
Reinforcement/Penalty
Regime
Reinforcement Component
0.560
0.334
0.871
Effector
Decision (=1)
Discovery component
• Genetic algorithm invoked once per iteration
• One new offspring is created, from parents
deterministically selected based on strength
• The single offspring replaces weakest
classifier in the population
Features of EpiCS
•
•
•
•
•
Object-oriented implementation
Stimulus-response architecture
Payoff/Penalty reinforcement regime
Syntactic control of overgeneralization
Differential penalty control of
undergeneralization
• Ability to compute risk of outcome
Discovering risk with EpiCS
• Output decision of the learning classifier
system is probability of disease (CSPD),
rather than dichotomous decision
• CSPD determined from proportion of
classifiers matching a given input case’s
taxon
Discovering risk with EpiCS:
The specifics
Classifiers
*10*0:1
0*100:0
01*00:1
0***0:1
CSPD 
Proportion
in match set
0.60
0.05
0.22
0.13
 (probabilities of classifiers associated with disease)
 (probabilities of all classifiers with matching taxa)

0.95
 0.95
1.0
Discovery of Predictive Models in
an Injury Surveillance Database:
An Application of Data Mining in Clinical Research
Partners for Child Passenger Safety
Information Infrastructure
State Farm
Insurance
Companies
CHOP
University of PA
Dynamic
Science, Inc.
Response
Analysis
Corporation
Why data mining is needed for PCPS
• Large number of raw and derived variables
renders traditional “manual” methods for
discovering patters in data unwieldy
• Hypothesis-driven (biased) analyses may
lead to missed associations
• Constantly changing patterns in prospective
data require constantly changing analytic
approaches that can be informed by data
mining
Candidate Predictors
• Demographics
• Kinematics
• Characteristics of crash
• Restraint use
Outcome: Head Injury
• Major burns involving the head
• Skull fracture
• Evidence of brain injury reported by
respondent
– Excessive sleepiness
– Difficulty in arousing
– Unresponsiveness
– Amnesia after accident
Data Preparation
• Pool of 8,334 records
• 20 separate datasets created
– All cases of head injury included (N=415)
– Equal number of non-head injury cases
randomly drawn from pool
• Each dataset randomly sampled to create
mutually exclusive training and testing sets
of equal size
Comparison methods:
Logistic Regression
• Variables from training sets stepped into model to
determine significant terms
• Significant terms used to create new risk model:
Pˆ y 
1
1 e
(  1 x1 ...   n xn )
• Risk model applied to cases in testing set
• Risk estimates categorized by deciles and used
construct ROC curves
Comparison Methods:
Decision Tree Induction
• C4.5 used to create decision trees from
training sets
• 10-fold cross-validation used to optimize
trees
• Optimized trees used by C4.5RULES to
classify cases in testing set
Experimental Procedure
for a=1 to maximum number of training epochs
for x=1 to 100
Training
present randomly selected training
Phase
case
for x=1 to number of training
cases
evaluate training case x
for x=1 to number of testing cases
evaluate testing case x
Genetic algorithm inactive
Interim
Evaluation
Phase
Training
Epoch
Trial
Testing
Epoch
Results: Training
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
AUC
0.2
Indeterminant Rate
0.1
0
0
1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
Iterations
Results: Training
• EpiCS
– 5,000 unique classifiers reduced to 2,314
by the end of training
• Logistic regression
– Single model with eight significant terms,
no significant interactions
• C4.5
– 11 rules created for each training set, most
with single conjuncts
Results: Prediction
Area under the ROC curve obtained on testing,
averaged over the 20 separate studies
EpiCS
0.97 (.04)
Logistic Regression
0.74 (0.03)
C4.5
0.79 (0.04)
And now for something a
little different
The XCS model
XCS: A little history
• Wilson, SW: Evolutionary Computation, 2(1), 1-18
(1994)
– ZCS
• Wilson, SW: Evolutionary Computation, 3(2), 149175 (1995)
– The seminal work on XCS
• Many papers by Lanzi, Barry, Butz, and others
• Butz, M and Wilson, SW: Advances in Learning
Classifier Systems. Third International Workshop
(IWLCS-2000), Lecture Notes in Artificial
Intelligence (LNAI-1996). Berlin: Springer-Verlag
(2001)
– The algorithm paper
What is XCS?
• An LCS that differs from traditional Holland
model
– Classifier fitness is based on the accuracy of
the classifiers payoff prediction, rather than
the prediction itself
– The genetic algorithm is restricted to niches in
the action set, rather than applied to the
classifier population as a whole
• The major feature is graceful, accurate
generalization
XCS in a nutshell
((43*99)+(27*3))/102
Action: 00
Action: 01
Source: Wilson, XCS tutorial
EpiXCS:
An XCS-Based Learning
Classifier System for
Epidemiologic Research
Outline
• What is it?
• EpiXCS architecture
– Data encoding
– Evaluation metrics
– Reinforcement
– Missing values handling
– Classifier ranking
– Risk assessment
• Test case: Pima Indians Diabetes Data
What is EpiXCS?
• Learning classifier system based on the
XCS paradigm
– Uses the Lanzi C++ kernel
• Designed for use in epidemiologic
research, specifically mining disease
surveillance databases in supervised
learning environments
– Visualization by non-LCS users
– Sensitive to demands of clinical data
Data Encoding in EpiXCS
• All numeric data formats permissible
–
–
–
–
Binary
Categorical
Ordinal
Real
• Non-binary data represented using “centerspread” approach
– Two genes per feature
• Actions are limited to binary (for now)
Sample input data format
(Pima Indians Diabetes Database)
ATTRIBUTE 0 <WILD "99"><REAL><STRING "Clump Thickness">
ATTRIBUTE 1 <WILD "99"><REAL><STRING "Uniformity of Cell Size">
ATTRIBUTE 2 <WILD "99"><REAL><STRING "Uniformity of Cell Shape">
ATTRIBUTE 3 <WILD "99"><REAL><STRING "Marginal Adhesion">
ATTRIBUTE 4 <WILD "99"><REAL><STRING "Single Epithelial Cell Size">
ATTRIBUTE 5 <WILD "99"><REAL><STRING "Bare Nuclei">
ATTRIBUTE 6 <WILD "99"><REAL><STRING "Bland Chromatin">
ATTRIBUTE 7 <WILD "99"><REAL><STRING "Normal Nucleoli">
ATTRIBUTE 8 <WILD "99"><REAL><STRING "Mitoses">
ACTION 9
<STRING "Malignant">
5 4 4 5 7 10 3 2 1 0
3111223110
8 10 10 8 7 10 9 7 1 1
…
Classifier Population Initialization
• Minima and maxima for each attribute
determined automatically at start of run
• Center values can be initialized by user
– Mean
– Median
– Random value between spread
• Spread values can be initialized by user
– Standard deviation
– Quantile
Sample Macroclassifiers
/5.5,5.5/107.5,51.5/64.0,21.0/#/316.0,160.0/16.55,16.55/#/#/:1
/3.0,3.0/#/91.5,30.5/#/#/#/#/26.0,5.0/:1
/2.5,2.5/119.5,63.5/#/#/#/#/#/#/:1
/2.5,2.5/107.5,51.5/64.0,21.0/#/#/#/#/49.0,28.0/:1
/2.5,2.5/#/66.0,22.0/#/317.5,301.5/#/1.0040,0.9260/49.0,28.0/:1
/2.5,2.5/107.5,51.5/64.0,21.0/#/#/#/1.0735,0.9955/#/:1
Evaluation Metrics
•
•
•
•
•
•
Sensitivity
Specificity
Area under the ROC curve
Predictive values
Accuracy
Learning rate
A Fast Primer on Test Evaluation
Test
Positive
Negative
Gold Standard
Positive
Negative
95
72
5
28
95
Sensitivity (True Positive Rate) 
 0.95
100
28
Specificity (True Negative Rate) 
 0.28
100
95
Positive Predictive Value 
 0.57
167
28
Negative Predictive Value 
 0.85
33
Sensitivity
• Prior probability of a test-positive
• If it’s high, then one would want to use the
test to diagnose (classify positive)
• If a classifier’s Se is high, then that classifier
should be more likely to be used in defining an
Correct Set when a training case is known positive
Specificity
• Prior probability of a test-negative
• If it’s high, then one would want to use the
test to rule out (classify negative)
• If a classifier’s Sp is high, then that classifier
should be more likely to be used in defining an
Correct Set when a training case is known
negative
The Predictive Values
• Posterior probability of a test-positive or negative
• If a PPV is high, then once one has the test
result in hand, and it predicts positive, it would
be considered to be accurate
• If a NPV is high, then once one has the test
result in hand, and it predicts positive, it would
be considered to be accurate
How these metrics are used in
EpiXCS
• To evaluate classification performance
– Training
• Se, Sp, AUC, Accuracy, and Indeterminate Rate
are plotted every 100th iteration
– Testing
• Se, Sp, AUC, Accuracy, and Indeterminate Rate
are obtained for the testing set
 AUCShoulder 
1000
 Shoulder 
 
How these metrics are used in
EpiXCS
• To evaluate learning
 AUCShoulder 
 
1000
 Shoulder 
– Shoulder is the iteration at which 95% of
the maximum AUC obtained during training
is first attained, and AUCShoulder is the
AUC obtained at the shoulder and
classification performance
Reinforcement in EpiXCS
• Done the usual way, but…
• User can bias the reward depending on
the class distribution
– Give disproportionately less “negative” reward
to False Negative classifiers in data with
<50% positives (where the Se is low)
– Give disproportionately less “negative” reward
to False Positive classifiers in data with <50%
negatives (where the Sp is low)
Missing Values Handling during
Covering
• Four possible ways to cover missing data in a nonmatching input σ that needs to be covered
– Wild-to-wild:
• Missing attributes covered as #s
– Random within range
• Random value within the range for the attribute
– Population average
• Population average for the attribute
– Population standard deviation
• Random value within the standard deviation for the attribute
Classifier Ranking
• After training, classifiers ranked according
to their predictive values
– Classifiers predicting positive ranked by PPV
– Classifiers predicting negative ranked by NPV
• Classifier ranking used for rule
visualization
Risk Assessment
• Based on risk assessment module used in
EpiCS
• Risk estimates determined on testing
based on proportional prevalence in match
sets for each testing case
• Provides risk assessment analogous that
obtained by logistic regression
Test case:
Pima Indians Diabetes Data
• 768 cases
– 268 positive, 500 negative
• 8 attributes
–
–
–
–
–
–
–
–
Gravidity
Plasma glucose
Diastolic blood pressure
Skin-fold thickness
Serum insulin
Body mass index
Pedigree function
Class: Diabetes Yes/No
Experimental procedure
• Training and testing sets created
– 134 positives/250 negatives in each
• EpiXCS
– Results averaged over 20 runs, 50,000 iterations
each
• See5
– Boosting at 10 trials
– 10-fold crossvalidation
• Logistic regression
– Relaxed stepwise model built on training set and
evaluated on testing set
Rules: EpiXCS
If Number of times pregnant is 7.0 ± 7.0
and plasma glucose concentration after 2 hours is 67.5 ± 11.5
and triceps skinfold thickness is 33.0 ± 26.0
and 2-hour serum insulin is 326.5 ± 66.5
and age is 48.0 ± 27.0
Then not diabetes
If Number of times pregnant is 7.5 ± 7.5
and triceps skinfold thickness is 35.5 ± 24.5
and 2-hour serum insulin is 811.5 ± 34.5
and body mass index is 48.9 ± 6.1
and pedigree function is 0.97 ± 0.89
Then diabetes
Rules: See5
Rule 9/1: (20.5, lift 1.8)
pedigree <= 0.179
age <= 34
-> class 0 [0.955]
Rule 9/2: (62.1/2.6, lift 1.8)
plasmaglu <= 103
pedigree <= 0.787
-> class 0 [0.944]
Rule 9/3: (9.3, lift 1.7)
serumins <= 156
bmi <= 35.3
age > 34
age <= 37
-> class 0 [0.912]
Rule 9/9: (12, lift 2.0)
plasmaglu > 135
serumins <= 185
bmi > 33.7
pedigree <= 1.096
age > 37
-> class 1 [0.928]
Rule 9/10: (37.1/2.5, lift 2.0)
plasmaglu > 103
bmi > 35.3
pedigree <= 1.096
age > 34
-> class 1 [0.909]
The logistic model
Risk of diabetes= 1.34
+ 0.19*Gravidity
+ 0.04*Post-prandial glucose
+ -0.01*Diastolic blood pressure
+ 0.01*Skinfold thickness
+ -0.01*Serum insulin
+ 0.05*Body mass index
+ 0.72*Pedigree function
Classification accuracy on testing
EpiXCS
Se
0.75 (0.06)
Sp
0.96 (0.04)
PPV
0.82 (0.02)
NPV
0.83 (0.03)
AUC
0.86 (0.04)
Learning
0.04 (0.001)
rate
0.79
0.92
0.59
0.89
0.86
Logistic
Regression
0.61
0.89
0.75
0.81
0.86
---
---
See5
Conclusions
• EpiXCS incorporates features of EpiCS
into the XCS paradigm
• Facilitates analysis of epidemiologic
data
• Uses metrics understood by clinical
researchers
• Discovers knowledge comparably to
See5 and logistic regression