Download 3D Inversion of magnetic total gradient data in the presence of

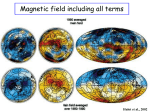
3D Inversion of magnetic total gradient data in the presence of remanent magnetization
Sarah Shearer* and Yaoguo Li
Gravity and Magnetics Research Consortium, Department of Geophysics, Colorado School of Mines
Summary
Inversion of magnetic data has long been hampered by the
need to specify the direction of magnetization. We present a
general approach that utilizes the minimal dependence on
magnetization direction of amplitude and total gradient data
and thereby overcome the difficulty associated with inversion
when unknown remanent magnetization is present. To
construct the inversion algorithm for the magnitude of
magnetization, we solve a nonlinear minimization problem
formulated using Tikhonov regularization. A positivity
constraint is also incorporated to improve the solution. The
algorithm will be illustrated with both synthetic and field data
sets.
Introduction
The presence of strong remanent magnetization can pose
severe challenges to the quantitative interpretation of
magnetic data. Problems stem from the fact that the direction
of total magnetization is unknown and can be significantly
different from that of the current inducing field. Thus, a vital
piece of a priori information is missing and the forward
modeling required in interpretation can no longer be reliably
carried out.
Although this problem has existed since the beginning of the
magnetic method, it has not received much attention for two
reasons. First, the remanence is either very weak or aligned
with the current field direction for the majority of
applications and therefore not of major consequence.
Secondly, many earlier interpretation techniques, such as
depth estimation methods (e.g., Hartman et al., 1971; Reid et
al., 1990), seek semi-quantitative information and are not
affected by the lack of unknown magnetization direction.
However, in applications such as crustal scale studies, mining
exploration, and archaeological investigations, the remanence
is often very strong and cannot be ignored. Inversion
techniques require recovered causative bodies to reproduce
the observed data, and this dictates that we must know the
magnetization direction. Unrealistic distribution of
magnetization and susceptibilities can result from inversion if
incorrect direction is specified.
Faced with this difficulty, one can take several different
approaches. The first is to physically measure the remanent
magnetization by oriented sample. This can be an expensive
proposition and a small number of samples may not
necessarily give good characterization of the bulk
magnetization direction. One can also attempt to estimate the
total magnetization direction by utilizing the properties of the
magnetic anomaly (e.g., Roest and Pilkington, 1993) and use
it in the interpretation.
An alternative approach is to work with quantities that are
computed from the observed magnetic data and have little or
no dependence on the magnetization direction. The wellknown analytic-signal approach by Nabighian (1972) belongs
to this class, in which it is shown that the amplitude of the
gradient (referred to as total gradient hence forth) in 2D is
independent of magnetization direction and its interpretation
yields source locations and geometry.
In an effort to invert for 3D magnetic source distribution in
the presence of remanence, Paine et al. (2001) examined two
related quantities. The first is the total gradient of the
vertically integrated magnetic anomaly (termed ASVI by
Paine et al.) and the second is the vertical integral of the total
gradient (VIAS). Because of the weak dependence and the
fact both quantities have the dimension of magnetic field, nT,
Paine et al. (2001) treated the quantities as RTP fields and
applied the 3D inversion algorithm by Li and Oldenburg
(1996). Compared to inverting total field anomaly by
assuming induced magnetization only, this approach has
produced somewhat better results. However, there are a
number of theoretical difficulties associated with this
approach and results are not always as expected.
This paper improves upon the work by Paine et al. (2001) by
developing an algorithm that directly inverts quantities
having a minimal dependence on the direction of the
magnetization. Such quantities include the magnitude of the
anomalous magnetic field vector and the magnitude of the
gradient vector of a magnetic anomaly. Our algorithm fully
incorporates the nonlinear relationship between these
quantities and the subsurface magnetization.
Theory
As discussed above, the horizontal and vertical derivatives of
the magnetic field can be combined into a two-dimensional
quantity known as the analytic signal, introduced by
Nabighian (1972). The amplitude of the analytic signal,
which is the amplitude of the gradient vector, is independent
of magnetization direction and allows for depth estimation
along the profile of a magnetic source without assumed
knowledge of magnetization.
Inversion of magnetic total gradient
Many authors have tried to extend this approach to 3D
problems, but to date no one has found a quantity that can be
calculated directly from the observed data and is entirely
independent of magnetization direction. However, it has
been demonstrated that the magnitude of the gradient vector
(total gradient), often erroneously termed 3D analytic signal,
has a minimal dependence on magnetization direction. In
particular, if the anomaly is half reduced to the pole, the
corresponding total gradient has an even weaker dependence
(Haney et al., 2003). Because of this property, total gradient
has been widely used for interpreting magnetic data acquired
in both exploration and environmental problems.
We can make use of this property and invert it directly to
recover the distribution of the magnitude of the
magnetization without knowing its direction. Figure 1
illustrates this property by displaying the total field anomalies
and the corresponding total gradients due to two identical
prismatic sources with different magnetization directions.
Although the total field anomalies are very different under
two different magnetization directions, the corresponding
total gradients appear to be similar. Since total gradient data
has minimal dependence on the magnetization direction, an
assumption of such will not drastically influence our results.
We note that the magnitude of the anomalous magnetic
vector itself has the similar property. The magnitude of the
anomalous field vector in 2D is also independent from the
magnetization direction. This arises from the fact that the
horizontal and vertical derivatives of magnetic potential
forms a Hilbert transform pair and the amplitude therefore
forms an envelope of either component. The envelope is, by
definition, independent of the direction. Although it is not
entirely direction independent in 3D, the amplitude can be
demonstrated as showing much less sensitivity to it.
Therefore, we can also invert it in the similar manner as we
do total gradient data.
It is interesting that the quantity ASVI used by Paine et al.
(2001) is equal to the amplitude of the anomalous field if the
observed magnetic data is converted to vertical component by
applying a half reduction to the pole. This is easily shown by
the fact that vertically integrating the vertical magnetic
anomaly yields the magnetic potential and the three partial
derivatives of the potential, which define the three
components of the anomalous field.
For brevity, we develop the inversion methodology below by
focusing on the total gradient, but note that it is exactly
parallel for the amplitude of the anomaly vector. Therefore,
the following algorithm is general and applicable to both.
The total gradient g is a calculated quantity defined using
partial derivatives of the anomalous field B in three
dimensions:
g = ∇B
=
(∂B / ∂x )
2
+ (∂B / ∂y ) + (∂B / ∂z )
2
2
,
(1)
where B is a given component of the anomalous field such as
the total field anomaly or the vertical anomaly. Given a set of
field data, the total gradient can be derived in different ways.
The horizontal derivatives can be calculated using a stable
algorithm in either the space or Fourier domain. The vertical
derivative is then obtained by applying the generalized 3D
Hilbert transform.
Forward modeling Given a subsurface magnetization model,
we can take a more direct approach to calculate its total
gradient. Assume the subsurface volume of interest is
discretized into a set of rectangular prisms with constant
magnetization. Let the values of the magnetization amplitude
be given by the product of an effective susceptibility κ and
the strength of the current inducing field. Denote the effective
v
susceptibility model by κ = (κ 1 , L , κ M ) T , where M is the
number of cells in the model. Each component of the gradient
is linearly related to the magnetization by a matrix system,
M
M
M
j =1
j =1
j =1
g xi = ∑ κ j G xij , g yi = ∑ κ j G yij , g zi = ∑ κ j G zij ,
(2)
where Gxij is the ∂B / ∂x produced at the i’th observation
location by unit susceptibility in the j’th cell. We have
implicitly assumed an anomaly projection direction and a
nominal magnetization direction, with the understanding that
the latter will not drastically affect the total gradient given by,
g ipred = g xi2 + g 2yi + g zi2 .
(3)
This process provides the mechanism to forward model the
predicted total gradient data from a given magnetization
model. It also is clear that the total gradient is nonlinearly
dependent upon the magnetization magnitude in each model
cell.
Inversion Given the above relationship between the
subsurface magnetization and the total gradient data, we can
perform a nonlinear inversion to recover the amplitude of
magnetization without knowing its exact direction. In
general, magnetic anomaly is a combined response of a
distribution of subsurface sources. Thus, we formulated the
inversion as an underdetermined problem. In addition,
observed magnetic data, and therefore the computed total
gradient, is contaminated with noise. To deal with these two
aspects, we use Tikhonov regularization (Tikhonov and
Arsenin, 1977) to formulate the inversion as an optimization
problem that minimizes the following objective function:
φ = φ d + βφ m ,
(4)
Inversion of magnetic total gradient
where φd is the data misfit, φm is the model objective
function, and β is the regularization parameter. The
regularization parameter is chosen to prohibit the model from
fitting noise-contaminated data exactly as well as to produce
a geologic level of features in the model.
The data misfit function is defined as
r
r
2
φd = Wd (d obs − d pre ) ,
v
d obs = ( g1obs , L , g Nobs )T
where
are
the
(5)
total
gradient
v
calculated from the observed magnetic data and d pre are the
predicted total gradient data, and Wd is a data weighting
matrix. The model objective function is designed to minimize
the structural complexity of the recovered effective
susceptibility,
r
r
2
φ m = Wm (κ − κo) ,
r
(6)
where κ = (κ1 , L, κ M )T is the effective susceptibility model
to be recovered, Wm is the model weighting matrix, and
is the reference susceptibility model.
r
κo
d
+
βφ m − 2 λ ∑ ln κ j ,
(7)
j
where λ is a barrier parameter. The logarithmic barrier term
ensures that feasible solutions of the minimization problem
are all positive.
Since the total gradient data are nonlinearly related to the
susceptibility model, and the logarithmic barrier term
introduces additional nonlinearity, the minimization problem
in eq. (7) must be carried out iteratively. We use a GaussNewton method. At each iteration, the model perturbation is
give by the following equation,
r
( J T WdT Wd J + βwTz wz + λΧ −2 )∆κ
,
r
r
v
= − J T WdT Wd δd n − βWmT Wmδκ n − λΧ −1e
The updated model is given by
v
(8)
v
r
r
r
v
r
r
r
where δd n = d n − d obs , δκ n = κ n − κ o , and, κ n and d n are
the model and predicted data at the n’th iteration. X is a
diagonal matrix containing the values of the current
susceptibility model and it stems from the presence of the
v
v
κ ( n+1) = κ ( n ) + α∆κ ,
(9)
where α is a step length determined by a linear search. This
v
process starts with an initial model κ ( 0) and a large value for
λ. The iteration terminates when the objective function has
stopped decreasing and the barrier parameter is sufficiently
small.
The majority of the computational cost for the inversion lies
in the solution of the Gauss-Newton equation in eq. (8) and
the calculation of the required sensitivity matrix J. For this
reason, we discuss the calculation of sensitivity next.
Sensitivity calculation The sensitivity matrix, J, characterizes
the change of the total gradient data with respect to
susceptibility values in the model. Substituting in eq. (2) into
eq. (1) and carrying out differentiation with respect to κ j
yields,
J ij =
In addition, we also impose a positivity constraint on the
recovered susceptibility model, for the magnitude of
magnetization is positive by definition. This is accomplished
by using a logarithmic barrier method, in which the constraint
is incorporated into the objective function as an additional
nonlinear term,
φ =φ
logarithmic barrier term. The matrix J is the sensitivity of
total gradient with respect to the effective susceptibility.
∂g i
1
=
∇Bipred ⋅ ∇bij ,
∂κ j
∇Bipred
(9)
where ∇Bipred is the gradient vector of the anomalous field
predicted by the current magnetization at the i’th observation
location and ∇bij is the magnetic gradient at the i’th location
due to unit susceptibility in the j’th cell. That is, the
sensitivity of the total gradient with respect to a particular
cell has a simple form: it is the inner product of the unit
directional vector of the gradient produced by the entire
model and the gradient produced by the unit susceptibility in
that cell.
We note that the components of ∇bij are the elements of
component sensitivity matrices Gx, Gy, and Gz in eq. (2).
These three matrices are therefore
v required in order to
calculate both the predicted data d ( n ) = ( g 1( n ) , L , g N( n ) ) T as
well as the sensitivity matrix J at each iteration. In our
algorithm, we first compute the three component sensitivity
matrices and store them for subsequent use since they model
independent. The calculation of sensitivity for total gradient
at each iteration is therefore a trivial operation that makes use
of the stored components. As a result, although the problem
is nonlinear, the computational cost to obtain a solution is
similar to that for solving the 3D magnetic inversion when
the magnetization direction is known.
Discussion
To overcome the restriction of requiring the direction of
magnetization in the presence of unknown remanent
Inversion of magnetic total gradient
magnetization, we have developed a 3D magnetic inversion
algorithm that utilizes the minimal dependence on
magnetization direction by quantities such as total gradient.
We first compute total gradient of observed total field
magnetic anomaly data and then invert the new data to
recover 3D variation of the amplitude of magnetization in the
subsurface. Although the forward modeling still requires an
assumed magnetization direction, it has little effect on the
inversion other than to facilitate the forward modeling.
The ability to invert magnetic data with little information
about the magnetization direction gives us is great flexibility
in practical applications. It is now possible to take any
magnetic data and carry out a 3D inversion to some extent.
This ability opens the door to applying 3D magnetic
inversion in a number of areas including the depth estimation
of basement in petroleum exploration, imaging kimberlites in
diamond exploration, and crustal studies.
Acknowledgments
The authors would like to thank Misac Nabighian for his
discussion. This work was partially supported by the Gravity
and Magnetics Research Consortium at the Colorado School
of Mines. One of the authors (SS) was supported by a
National Science Foundation Grant award # DGE0231611.
Hartman, R.R., Teskey, D.J., and Friedbery, J.L., 1971, A
system for rapid digital aeromagnetic interpretation:
Geophysics, 36, 891-918.
Li, Y., and Oldenburg, D.W., 1996, 3-D inversion of
magnetic data: Geophysics, 61, 394-408.
Nabighian, M., 1972, The analytic signal of two-dimensional
magnetic bodies with polygonal cross-section: its properties
and use for automated anomaly interpretation: Geophysics,
37, 507-517.
Paine, J., Haederle, M., and Flis, M., 2001, Using
transformed TMI data to invert for remanently magnetized
bodies: Exploration Geophysics, vol. 32, no. 3 & 4, 238-242.
Reid, A. B., Allsop, J. M., Granser, H., Millett, A. J., and
Somerton, I. W., 1990, Magnetic interpretation in three
dimensions using Euler deconvolution: Geophysics, 55, 80–
91.
Roest, W. R. and Pilkington, M., 1993, Identifying remanent
magnetization effects in magnetic data: Geophysics, 58, 653659.
Tikhonov, A. and Arsenin, V., 1977, Solutions of ill-posed
problems, V.H. Winston & Sons.
References
Haney, M., Johnston, C., Li, Y., and Nabighian, M., 2003,
Envelopes of 2D and 3D magnetic data and their relationship
to the analytic signal: 73rd Ann. Internat. Mtg., Soc, Expl.
Geophys., Expanded Abstracts.
Im=65º
Dm=25º
Im=25º
Dm=-65º
Figure 1: An illustration of the weak dependence on magnetization direction by total gradient data (the amplitude of the gradient
vector). The assumed inducing field is in the direction of I=45º and D=45º. The total field anomalies produced by two identical
prismatic sources with different magnetization directions (Im and Dm) appear very different, whereas the corresponding total
gradients are much more similar. Thus, the assumption of total gradient’s minimal dependence on the magnetization direction
will not drastically influence inversion results. This is especially true after the total field data are converted to vertical anomaly.