Download Attention Graduate Students Introduction to Plasma Physics Physics

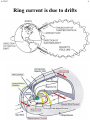
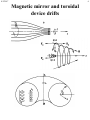
8/2/2017
1
Particle in uniform B-field
•
Equation of motion of a particle of charge qs = se
(s = ±1, for s = i, e) in a given uniform magnetic field, B0,
pointing in the z-direction
z, B
0
•
Dot v into both sides to show that v2 = const.
y
x
– Magnetic field can do no work on particles.
• Can’t change their kinetic energy, but can change their momentum.
•
Decompose particle velocity, v, into components parallel and
perpendicular to B:
– v = v|| + v
•
Parallel and perpendicular motions are independent
– Parallel velocity, v|| is constant. Parallel motion is free-streaming.
– Since v2 is constant, so is the magnitude v = |v|
– Perpendicular motion is circular around B (looking down on B).
• Both r and v rotate at the cyclotron frequency, s
• Ions move clockwise, electrons counterclockwise
– Combined motion is spiraling parallel or antiparallel to B
•
Lorenz force provides centripetal acceleration in perp plane
z, B0
ions
Ri
x
vi
z, B0
ve
y
electrons
y
x
Re
8/2/2017
2
Gyromotion and Drifts
• Constant magnetic field, B in z-direction: v||, |v| = const
• Constant B and constant force, F
– Electrons drift opposite from ions unless F = seE. In the
electric force they both drift the same way:
1
ˆ
vDrift = c E^ ´ B
0
B0
• Inhomogeneous straight magnetic field lines
– Example of B = (0, 0, B(y)), (note, ·B = 0 )
– Constant drift, vD, smaller than local gyrospeed, u, is approximate solution when gradient scale length, Ly, is large
compared to local gyroradius and drift motion is time-averaged
8/2/2017
3
Drifts and Adiabatic Invariants
• Curvature drift
– Let Rc be the radius of curvature of a magnetic field line
with constant magnitude, B.
– Let v|| be the parallel velocity (curving) of particles
gyrating along that field line.
– The curvature drift, vc, is orthogonal to both the local B and
the local radius of curvature vector Rc (i.e. is azimuthal for
a cylindrically symmetric set of curved field lines) and
given by the following expression:
B
• Magnetic moment
Rc
– The magnetic moment  provides a simple way to
understand the effective parallel force on the guiding center
of a particle s = e, i gyrating along a magnetic field line (in
z-direction) when surrounding field lines are converging or
diverging. The relation between the force and the gradient
of the magnetic field is:
F||eff = - s ∂zBz or more generally, F|| = -s·B
– The magnetic moment is an approximate (adiabatic)
invariant of the motion of the guiding center when the
timescale for motion of the guiding center is slow
compared to the gyrofrequency (parallel force small
compared to perpendicular force causing gyromotion)
smsv2/2B
8/2/2017
4
Ring current is due to drifts
8/2/2017
5
Van Allen Belt trapped electrons NASA Website:
http://www-istp.gsfc.nasa.gov/Education/wtrap1.html
Charged particles--ions and electrons--can be trapped by the Earth's
magnetic field. Their motions are an elaborate dance--a blend of three
periodic motions which take place simultaneously:
1. A fast rotation (or "gyration") around magnetic field lines, typically
thousands of times each second.
2. A slower back-and-forth bounce along the field line, typically
lasting 1/10 second.
3. A slow drift around the magnetic axis of the Earth, from the current
field line to its neighbor, staying roughly at the same distance. Typical
time to circle the Earth--a few minutes.
View from North Pole
Because positive ions and negative electrons drift in opposite directions,
that motion will create an electric current that circulates clockwise
around the Earth when viewed from north. The current is aptly named the
ring current.
The magnetic field produced by the ring current contributes (rather
slightly) to the magnetic field observed at the surface of the Earth. There
are however times when the population of trapped particles is greatly
reinforced. The ring current then becomes stronger and its magnetic
effect at Earth may grow 10-fold or more: that is known as a magnetic
storm.
8/2/2017
6
Magnetic mirror and toroidal
device drifts