Download Chapt33_VGo

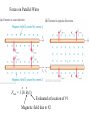
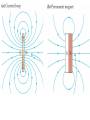
Chapter 33. The Magnetic Field
1. Moving charges make a magnetic field
2. The magnetic field exerts a force on moving charges
Thus moving charges exert forces on each other (Biot Savart Law)
3. A collection of moving charges constitutes and electrical current
4. Currents exert forces and torques on each other
1. Moving cha rges (or equivalently electric al currents) create a magne tic field,
r
 qv  r̂
B(r)  0
,
2
4 r
*
r
Here v is the velocit y o f t he moving cha rge.
This is the ana log to the expr ession for the e le ctric field due to a point cha rge.
r r
E(r) 
q
r̂
4 0 r 2
Supe rpositi on app li es if a nu mber of mov ing cha rges are present just as in the c ase of
electric fields. As in the c ase of e lectric fields, mo st of you r grief will come from trying
to apply the principle of sup erposition.
* This isn’t really true but pretend for the moment that it is.
2. A cha rge moving through a magne tic field feels a force (calle d the Lorenz force)
given by
r r
F  qv  B .
The total electric and magne tic force on a moving ch arged particle is the sum of the
contribution s due to electric and magne tic fields,
r
r r r
F  q(E  v  B) .
Just to be confu sing this is sometim es call ed the Lorenz force too.
Ther e are a ho st of consequen ces of 1. and 2. , which will be exp lored in this
chap ter. An ex ample is parallel curre nts attra ct and antipara llel curre nts repel.
A big complic ation when discussing magne tic fields is the appearance of vector
cro ss products. Don’t think that you can sli de by wit hout learning how to evaluate them.
Electric Field
r
E(r) 
Magnetic Field
r
0 qv  r̂
r
B(r) 
4 r 2
q
r̂
4 0 r 2
r̂
v
q
r
What are the magnitudes
and directions of the
electric and magnetic
fields at this point?
Assume q > 0
Comparisons: both go like r-2, are proportional to q, have 4 in
the denominator, have funny Greek letters
Differences: E along r, B perpendicular to r and v
Greek Letters
r
E(r) 
r
0 qv  r̂
r
B(r) 
4 r 2
q
r̂
4 0 r 2
 0  8.8542 1012 Farads / meter
0  4 107
Henries / meter
Huh?
These funny numbers are a consequence of us having
decided to measure charge in Coulombs
Later we will find:
1/  0 0  c
0 /  0  377 Ohms
Aside on cro ss produc ts:
r r
CAB
r
C
r
B

r
A
r
r
Let  be the ang le between A and B , always chose this to be less than 180°.
r
r
r r
The magn it ude of C is given by C  A B sin 
r
r
r
The d ir ection o f C is perpend icula r to both A and B , and de termined by the “right hand
rule”
Right hand rule: put the finger s of you r right hand in the d irrection of A , then rotate
them through the ang le  (less than 180 °) to the d ir ection of B . Your thumb now
r
indicates the direction o f C .
r
r
r r r
r r
The o rder of A and B is important: C  A  B  -B  A
r
r
r
If A and B are parall el, then (C = 0 .
Let’s say w e are given A and B in compon ent form i n C artesian coordinates.
r
A  Ax î  Ay ĵ + Az k̂
.
r
B  Bx î  By ĵ + Bz k̂
r
How do we find the componen ts of C ?
r
C  C x î  C y ĵ + C z k̂ .
Answer:
C x  Ay Bz  Az By
C y  Az Bx  Ax Bz
(my favorite)
C z  Ax By  Ay Bx
Same result as:
î
Ax
ĵ
Ay
k̂
Az
Bx
By
Bz
The positive charge is
moving straight out of the
page. What is the direction
of the magnetic field at the
position of the dot?
r
0 qv  r̂
r
B(r) 
4 r 2
A. Left
B. Right
C. Down
D. Up
Field near a point charge
QuickTi me™ and a
Graphics decompressor
are needed to see this picture.
Field lines emerge from
charges
Iron filings align parallel to magnetic field
Field lines do not end
Magnetic field due to a
single loop of current
Electric field due to a dipole - two
opposite charges separated by a
distance
Magnets are objects that have charges moving inside them
Electrical currents
Magne ts have “po les” labeled north and south:
Like poles repel
S
N
N
S
N
S
N
Unli ke poles attract
S
If you cu t a magne t in half, both halves will hav e a no rth and south po le .
Cut
S
S
N
N
S
N
33.7 Force on a mov ing Charge
For a stationa ry charg e we have
r r
F  qE(r) .
For a moving cha rge ther e is an addit ion al contribution , kno wn as the Lorenz force,
r
r r r
F  q(E  v  B) .
r
Here, v is the velocit y o f t he moving cha rge.
Some facts:
r
1. For a particle at rest, v = 0 the magne tic field exer ts no force on a charged pa rticle.
2. The Lorenz force is proportion al to the cha rge, the magne tic field streng th and the
particle’s velocity.
3. The vec tor force is t he result of the vec tor cross produ ct of ve locit y and ma gne tic
field.
Motion of a cha rged p article in a magne tic field
r
r r
Newton’s law: ma  F  qv  B
r
dv
r
r r
ma = m
 qv  B
dt
Note: Lorentz force is always perpend icular to velocit y. There fore the magn it ude o f
velocit y will not change. This impli es the kinetic ene rgy o f the particle is constant,
d
m r2
r r
KE  v  F = 0 ,
KE  v
dt
2
Note also, if ve locity is parall el to ma gne tic field the force is zero and ve ctor velocit y is
constant.
Does the compass needle rotate clockwise
(cw), counterclockwise (ccw) or not at all?
A. Clockwise
B. Counterclockwise
C. Not at all
Does the compass needle feel a force from
the charged rod?
A. Attracted
B. Repelled
C. No force
D. Attracted but very weakly It’s complicated
z
B = 1T in the y direction
y
x
r vr =
v
60°
106 m/s in x-y plane
What is the force on a moving electron?
r r
F  q(v  B)
r
r r
v  B  v B sin 
1)
F  1.6  10 (C) *10 (m / s) *1(T ) * k
2
)
13
F  0.8 10 k Newtons
19
6
What is  in this problem?
A. 60°
B. 30°
C. 72 ° and sunny
r r
F  q(v  B)
Cyclotron Motion
r r
F  q(v  B)
rcyc
Newton’s Law
r r
ma = F
Both a and F directed toward
center of circle
r
v2
a=
rcyc
r
F = qvB
Equate
v
qB
W=
=
= 2p fcyc
rcyc
m
v
v
rcyc = =
W 2p fcyc
r r
F  q(v  B)
rcyc
In this picture B is pointing into
the page and q is positive.
What changes if q is
negative and B points out of
the page
A. Rotation changes to
counter-clockwise
B. There is no change
C. Why do things always have
to change?
r r
F  q(v  B)
rcyc
In this picture B is pointing into
the page and q is positive.
What changes if q is
negative and B points out of
the page
A. Rotation changes to
counter-clockwise
B. There is no change
C. Why do things always have
to change?
Some Examples
qB
fcyc =
2p m
Ionosphere at equator
- 5
B ; 3.5¥ 10 T
Te ; 300o K
v ; 6¥ 10 4 m / s
fcyc ; 106 Hz
rcyc ; .01m
ITER fusion exp
B ; 6T
Te ; 10 8
v ; .2c
o
fcyc ; 1.67 1011 Hz
K
rcyc ; 5.7¥ 10- 5 m
v
rcyc =
2p fcyc
Motion of a charged particle in crossed
electric and magnetic fields
E
y
.
z
x .
v
B
Try these
r
v = vx i
r
E = Ey j
r
B = Bz k
r
r r r
dv
m = q E + v¥ B = jq(Ey - vx Bz )
dt
(
)
If vx=Ey/Bz force is zero and no acceleration
Particle will move at a constant velocity in a direction
perpendicular to both E and B
Where are you most likely to encounter E cross B motion?
A. Your doctor’s office
B. Your Kitchen
C. The bridge of the Starship Enterprise
Where are you most likely to encounter E cross B motion?
A. Your doctor’s office
B. Your Kitchen
C. The bridge of the Starship Enterprise
B-out of page
Magnetron
Electrons spiral out from the
cathode K toward anode A.
Potential energy is converted
into radiation, f=2.45 GHz
Radiation then converted
into popcorn
B, V0 and Slots in anode define radiation frequency
Current carrying wire
Inside the wire there are stationary
charges and moving charges.
Metallic conductor
Moving - free electrons
Stationary - positive ions and bound
electrons
In any length of wire the number of positive and negative
charges is essentially the same (unless the wire is charged).
The wire can carry a current because the free electrons move.
Current, number density and velocity
Number density, n, of free
electrons is a property of the
material.
For copper n ; 1.1¥ 10 29 m- 3
Consider a segment of length l,
cross sectional area A
A
The segment has N free electrons
N = n (lA)
volume
Suppose the free electrons have speed v. How long will it take all
the electrons to leave the segment?
Dt = l / v
Current
During a time interval Dt = l/v, a net charge Q = -eN flows through
any cross section of the wire.
The wire is thus carrying I
Q
eNv
I=
=
Dt
l
The current is flowing in a
direction opposite to that
of v.
A
How big is v for typical currents in copper?
A.
B.
C.
D.
A
Close to the speed of light
Supersonic
About as fast as a Prius
Glacial
How big is v for typical currents in copper?
A.
B.
C.
D.
Close to the speed of light
Supersonic
About as fast as a Prius
Glacial
A
For a 1mm radius copper wire carrying 1 A of current
I
v=
= 1.8¥ 10- 5 m / s
Aen
What is the force on those N
electrons?
Force on a single electron
r
r r
F = - e v¥ B
(
)
Force on N electrons
Now use
r
eN v = I l
r
r
Lets make l a vector - eNv = I l
Force on wire segment:
r
r r
F = - eN v¥ B
(
)
points parallel to the wire in
the direction of the current
when I is positive
r r
r
Fwire = I l ¥ B
r r
r
Fwire = I l ¥ B
Comments:
Force is perpendicular to both B and l
Force is proportional to I, B, and length of line segment
Superposition: To find the total force on a wire you must break
it into segments and sum up the contributions from each
segment
r
Ftotal = I
Â
segments- i
r r r
li ¥ B(ri )
What is the force on a rectangular loop?
Net force is zero
Torque on a loop
Plane of loop is tilted by angle  with respect to direction of B.
The loop wants to move so that its axis and B are aligned.
Definition of torque
r
t =
r r
 r¥ F
sides
Êa ˆ˜
t y = 2Á
˜˜ IbBsin q = i(ab)Bsinq
Á
Á
Ë2 ¯
Nuclear magnetic resonance Basis of MRI magnetic resonance imaging
Magnetic Field due to a current
r
0 qv  r̂
r
B(r) 
4 r 2
Magnetic Field due to a single charge

r
B(r)  0
4
If many charges use superposition
r
qi v i  r̂i
 r2
ch arg esi
i
r̂1
r̂2
r3
r̂3
r2
#3 q3 , v3
#2 q2 , v2
#1 q1, v1
r1
Where I want to know what B is
For moving charges in a wire, first sum over charges in each
segment, then sum over segments


r
0
q
v

r̂
0
r
i i
i
 
B(r) 


4 sgments j  ch arg es in
ri 2  4
 each segment i


ch arg es in
each segment i
r
r
l j  r̂j
qi v i  r̂i

I
ri 2
rj 2

sgments j
I
r
l j  r̂j
rj 2
Summing over segments - integrating along curve
I
r
dl
r
r̂
r
r

r
B(r)  0
4
Biot Savart law

I
r
l j  r̂j
sgments j
rj 2
r

dl  r̂
 0—
I
4 
r2
Integral expression looks simple but…..you have to keep track
of two position vectors
r
r
which is where you want to know B
which is the location of the line segment that is contributing to
B. This is what you integrate over.
Magnetic field due to an infinitely long wire
z
Current I flows along z axis
r
0
dl  r̂
r
B(r) 
I
4 
r2
I
I want to find B at the point
r = xi  0 j  0k
r̂
x
r r
r = r - r¢ =
r
dl = dz¢k
r r
r - r¢
xi - z¢k
r̂ = r r =
r - r¢
x 2 + z¢2
x 2 + z¢2
r  = 0i  0 j  zk
I will sum over segments at points
r
0
dl  r̂
r
B(r) 
I 2

4
r
r
dl = dz¢k
r r
r - r¢
xi - z¢k
r̂ = r r =
r - r¢
x 2 + z¢2
0
j
0 I dz x k  i - zk  k 
r
B(r) 
 x 2  z2 3/2
4 

r r
r = r - r¢ =

dz x j
0 I
0 I
r
B(r) 
3/2 

2
2
4  x  z
2 x


See lecture notes
x 2 + z¢2
r
0 I
B 
2 r
compare with E-field for a line charge

E 
2 0 r
Forces on Parallel Wires
r r
F2on1 = I l1 ¥ B2 (1)
Evaluated at location of #1
Magnetic field due to #2
r r
F2on1 = I l1 ¥ B2 (1)
Evaluated at location of #1
Magnetic field due to #2
r
mI
B2 (1) = 0 2
2pd
Direction out of page for positive
What is the current direction in the loop?
A. Out of the page at the top of the
loop, into the page at the bottom.
B. Out of the page at the bottom of the
loop, into the page at the top.
Magnetic field due to a loop of current
See derivation in
book
R
Contribution from top
Bz
Contribution from bottom
Note: if z >> R
r
m0 I
R2
B(r = 0, z) =
2 (R2 + Z 2 )3/2
r
m0 I R2 m0 ( IA)
B(r = 0, z) ;
=
3
2 Z
2p Z 3
Magnetic moment,
Independent of loop
shape
What is the current
direction in this loop?
And which side of the
loop is the north pole?
A. To the right in front, north pole on bottom
B. To the left in front; north pole on bottom
C. To the right in front, north pole on top
D. To the left in front; north pole on top
Coulombs Law implies
Gauss’ Law and
conservative E-field
Gauss’ Law:
r
E(r) 
q1
4 0 r
2
r̂
r r r
0—
 E(r)  ds
r Qin
—
 E  dA 
0
But also, Gauss’ law and
conservative E-field imply
Coulombs law
r
E(r) 
q1
4 0 r
2
r̂
Biot-Savart Law
implies Gauss’ Law
and Amperes Law
Gauss’ Law:
q r
r
B(r)  0 12 v  r̂
4 r
r
—
 B  dA  0
Ampere’s Law
r r
—
 B(r)  ds =0 Ithrough
But also, Gauss’ law and
Ampere’s Law imply the Biot Savart law
0 q1 r
r
B(r) 
v  r̂
2
4 r
Consequences of Coulomb’s Law
Gauss’ Law:
r Qin
—
 E  dA 
0
Electric flux leaving a closed
surface is equal to charge
enclosed/o
Always true for any closed surface! Surface does not need to
correspond to any physical surface. It can exist only in your head.
Surface used to calculate
electric field near a line
charge
Magnetic field due to a
single loop of current
Electric field due to a single charge
Guassian surfaces
QuickTi me™ and a
Graphics decompressor
are needed to see this picture.
r
—
 B  dA  0
r Qin
—
 E  dA 
0
Further consequences of CL
Existence of
a potential
r r r
V(rf )  V(ri )    E(r)  ds
ri
r
E(r)
V (rf ) rf
r
ds
V (ri ) ri
Difference in potential
is independent of path
between ri and rf
rf
r
E(r)
r r r
0—
 E(r)  ds
r
ds
Line integral around
any closed loop is zero.
Field is “conservative”
r r
—
 B(r)  ds  0 I
r
B(r)
r r r
0—
 E(r)  ds
r
E(r)
r
ds
r
ds
r
ds
Right hand rule: direction of ds
determines sign of I
QuickTi me™ and a
Graphics decompressor
are needed to see this picture.
For the path shown, what is
r r
B(
r)
—
  ds  ???
A:
B:
C:
D:
I1 + I2 + I3+I4
I2 - I3+I4
-I2 +I3-I4
something else
Does I1 contribute to B at
points along the path?
A: Yes
B: No
r r
—
 B(r)  ds  0 I
r
r r
—
 B(r) ds  2 d B(d)
Thus
o I
B(d) 
2 d
Agrees with Biot-Savart
r r
—
 B(r)  ds  0 Ithrough
r r
—
 B(r)  ds  2 r B(r)
Ithrough  I if
I through
r2
 2I
R
if
rR
rR
r r
—
 B(r)  ds =0 Ithrough
r r
B(
r)
ds =Bl
—

0 I through  0 NI
B
0 NI
l
 0 (N / l)I
# turns per unit length
Coulombs Law implies
Gauss’ Law and
conservative E-field
Gauss’ Law:
r
E(r) 
q1
4 0 r
2
r̂
r r r
0—
 E(r)  ds
r Qin
—
 E  dA 
0
But also, Gauss’ law and
conservative E-field imply
Coulombs law
r
E(r) 
q1
4 0 r
2
r̂
Biot-Savart Law
implies Gauss’ Law
and Amperes Law
Gauss’ Law:
q r
r
B(r)  0 12 v  r̂
4 r
r
—
 B  dA  0
Ampere’s Law
r r
B(
r)
—
  ds =0 Ithrough
But also, Gauss’ law and
Ampere’s Law imply the Biot Savart law
0 q1 r
r
B(r) 
v  r̂
2
4 r