* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Section 5-2
Interpretations of quantum mechanics wikipedia , lookup
Renormalization wikipedia , lookup
Hartree–Fock method wikipedia , lookup
Quantum teleportation wikipedia , lookup
Quantum state wikipedia , lookup
Copenhagen interpretation wikipedia , lookup
Molecular Hamiltonian wikipedia , lookup
Canonical quantization wikipedia , lookup
History of quantum field theory wikipedia , lookup
Franck–Condon principle wikipedia , lookup
X-ray photoelectron spectroscopy wikipedia , lookup
EPR paradox wikipedia , lookup
X-ray fluorescence wikipedia , lookup
Rutherford backscattering spectrometry wikipedia , lookup
Particle in a box wikipedia , lookup
Hidden variable theory wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Molecular orbital wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Tight binding wikipedia , lookup
Matter wave wikipedia , lookup
Hydrogen atom wikipedia , lookup
Wave–particle duality wikipedia , lookup
Atomic theory wikipedia , lookup
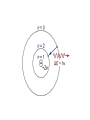
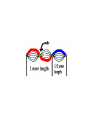
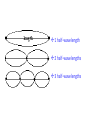
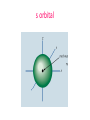
Section 5-2 Quantum Theory and the Atom Objectives • Compare the Bohr and quantum mechanical models of the atom • Explain the impact of de Broglie’s waveparticle duality and the Heisenberg uncertainty principle on the modern view of electrons in atoms • Identify the relationships among a hydrogen atom’s energy levels, sublevels, and atomic orbitals Bohr (1913) • Proposed the quantum model for H • Based on Planck/ Einstein’s quanta energy • H atom has only certain allowable energy states • Lowest = ground state • Gaining energy = excited state Continued • Electrons move in certain, specific, circular orbitals • Smaller orbit = lower energy level • Assigned the allowable electron orbitals the principle quantum number, n. • 1st orbit= lowest energy: n=1 • 2nd orbit= 2nd lowest energy: n=2 De Broglie (1924) • Electrons, like light, have particle-wave dual nature • Only multiples of 1/2 wavelengths allowed in circular orbits 1 half-wavelength 2 half-wavelengths 3 half-wavelengths Continued • All moving particles behave like waves • Wave characteristics decrease as mass increases h mv Heisenberg Uncertainty Principle –Fundamentally impossible to know precisely both velocity AND position of a particle at the same time –Cannot measure an object without disturbing it Schrödinger (1926) • Quantum mechanical model –Limited electrons to only certain energy levels Quantum Mechanical Model • Principal quantum numbers (n) – n = number of principle energy levels – Lowest level= ground state= n= 1 • Inside of principle energy levels are sublevels – s, p, d, f • Inside sublevels are orbitals – s has 1, p has 3, d has 5, f has 7 • Inside each orbital are 2 electrons s orbital Three p orbitals Five d orbitals Seven f orbitals Look at Table 5-2 (p. 134)