Download Alpha-Beta Example

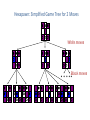
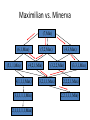
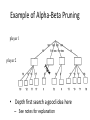
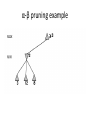
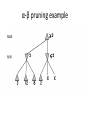
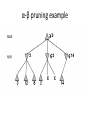
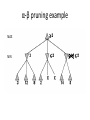
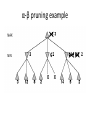
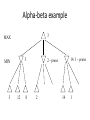
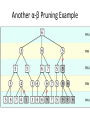
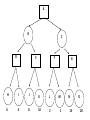
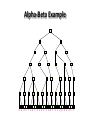
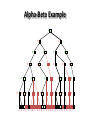
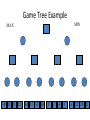
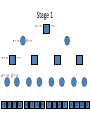
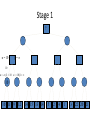
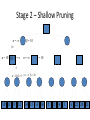
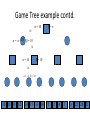
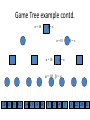
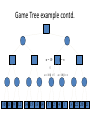
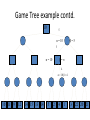
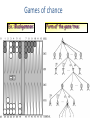
Artificial Intelligence
Game Playing
State of the art
State of the art
AI Game
• Game is primarily behavioral, since this is how
player’s perceive the intelligence
• Game is not focused on winning – it enhances
play and enjoyment
Rock-paper-scissors
Column player Ahmed player 2 (simultaneously) chooses a column
Row player
Ahmed player 1
chooses a row
A row or column is
called an action or
(pure) strategy
0, 0 -1, 1 1, -1
1, -1 0, 0 -1, 1
-1, 1 1, -1 0, 0
Row player’s utility is always listed first, column player’s second
Zero-sum game: the utilities in each entry sum to 0 (or a constant)
Three-player game would be a 3D table with 3 utilities per entry, etc.
“Chicken”
• Two players drive cars towards each other
• If one player goes straight, that player wins
• If both go straight, they both die
S
D
D
S
D
D
S
S
0, 0 -1, 1
1, -1 -5, -5
not zero-sum
Virtua Fighter 2 & 4
• Virtua Fighter 2 opponents
could do basic pattern
recognition (learn favored
moves and sequences) to
determine which countermoves to use
• Virtua Fighter 4 allows you to
train a fighter to use your
moves and combos, then have
them fight for you
Creatures 1, 2 & 3
• Creatures uses neural nets to learn behaviors over time
and genetic algorithm concepts to breed neural nets
and creatures
• This game is an example of Artificial Life
Half-life
• Uses “schedule-driven state machines” to control’ behavior
– The state determines the schedule of behavior available
to it
• Uses flocking and formation rules to control squad behavior.
Unreal
• Unreal has enemy flocking behaviors, similar to Half-life
• Unreal has extensive script language that allows the development
of AI bots
The Sims
– Embeds behavior code in the objects themselves
• How to do the behaviors
• Conditions for the behaviors
– An object-oriented approach
– Allows a VERY extensible environment
Racing Games
• Dirt Track Racing : Uses neural networks to control opponent driving
• Formula 1 Grand Prix 2 : Opponent driving styles based on real
Formula 1 drivers
• General ideas:
– Most opponents use pre-stored information on how to approach
upcoming track
– Opponents could be trained based on real drivers with specific
styles of driving
Game playing
• Many similarities to search
• Most of the games studied
– have two players,
– are zero-sum: what one player wins, the other loses
– have perfect information: the entire state of the game is known to
both players at all times
• E.g., tic-tac-toe, checkers, chess, Go, backgammon, …
• Will focus on these for now
• Recently more interest in other games
– Esp. games without perfect information; e.g., poker
• Need probability theory, game theory for such games
Types of Games
Perfect Information Games
• We consider 2 players perfect information games
• Perfect Information: both players know everything
there is to know about the game position
– no hidden information
– no random events
– two players need not have same set of moves
available
– examples are Chess, Go, Checkers, O’s and X’s
15
Game Trees
• A game tree is like a search tree
– nodes are search states, with full details about a
position
– edges between nodes correspond to moves
– leaf nodes correspond to determined positions
• e.g. Win/Lose/Draw
• number of points for or against player
– at each node it is one or other player’s turn to move
16
Basis of Game Playing:
Search for best move every time
Search for
Opponent
Move 1
Moves
Initial Board State
Board State 2
Search for
Opponent
Move 3
Moves
Board State 4
Board State 3
Board State 5
Relation of Games to Search
• Search
– Solution is (heuristic) method for finding goal
– Heuristics can find optimal solution
– Evaluation function: estimate of cost from start to goal through
given node
– Examples: path planning, scheduling activities
• Games
– Solution is strategy (strategy specifies move for every possible
opponent reply).
– Time limits force an approximate solution
– Evaluation function: evaluate “goodness” of game position
– Examples: chess, checkers, Othello, backgammon
Coping with impossibility
• It is usually impossible to solve games completely
• This means we cannot search entire game tree
– we have to cut off search at a certain depth
• like depth bounded depth first, lose
completeness
• Instead we have to estimate cost of internal nodes
• Do so using evaluation function
19
Evaluation functions
• Evaluations how good a ‘board position’ is
– Based on static features of that board alone
• Zero-sum assumption lets us use one function to describe
goodness for both players.
– f(n)>0 if we are winning in position n
– f(n)=0 if position n is tied
– f(n)<0 if our opponent is winning in position n
• Build using expert knowledge,
– Tic-tac-toe: f(n)=(# of 3 lengths open for me)
- (# open for you)
20
Example Chess Score
• Black has:
– 5 pawns, 1 bishop, 2 rooks
• Score = 1*(5)+3*(1)+5*(2)
= 5+3+10 = 18
White has:
– 5 pawns, 1 rook
• Score = 1*(5)+5*(1)
= 5 + 5 = 10
Overall scores for this board state: black
= 18-10 = 8
white = 10-18 = -8
Some Chess Positions and their Evaluations
White to move
f(n)=(9+3)-(5+5+3.25)
=-1.25
… Nxg5??
f(n)=(9+3)-(5+5)
=2
So, considering our opponent’s possible
responses would be wise.
22
Uh-oh: Rxg4+
f(n)=(3)-(5+5)
=-7
And black may
force checkmate
Hexapawn: Simplified Game Tree for 2 Moves
  
  
White moves
  
  

  

 



 
…..
Black moves





 
 
 
 

 

 
 
 

 



 
 






For Trivial Games
• Draw the entire search space
• Put the scores associated with each final board
state at the ends of the paths
• Move the scores from the ends of the paths to the
starts of the paths
– Whenever there is a choice use minimax assumption
– This guarantees the scores you can get
• Choose the path with the best score at the top
– Take the first move on this path as the next move
Entire Search Space
O’s and X’s
• A simple evaluation function for O’s and X’s is:
– Count lines still open for me (maX),
– Subtract number of lines still open for you (min)
– evaluation at start of game is 0
• Evaluation functions are only heuristics
– e.g. might have score -2 but maX can win at next move
•O - X
•- O X
•- - • Use combination of evaluation function and search
26
A Partial Game Tree for Tic-Tac-Toe
f(n)=6-6=0
f(n)=6-4=2
f(n)=4-4=0
f(n)=4-3=1
-∞
27
f(n)=2
f(n)=2
f(n)=2
f(n)=2
f(n)=2
f(n)=2
f(n)=0
f(n)=0
f(n)=4-3=1
0
f(n)=2 f(n)=2
f(n)=4-2=2
+∞
f(n)=# of potential three-lines for X –
# of potential three-line for Y if n is
not terminal
f(n)=0 if n is a terminal tie
f(n)=+ ∞ if n is a terminal win
f(n)=- ∞ if n is a terminal loss
CSE 391 - Intro to AI
MiniMax
• Assume that both players play perfectly
– Therefore we cannot optimistically assume player will
miss winning response to our moves
• Consider Min’s strategy
– wants lowest possible score, ideally - 
– but must account for Max aiming for + 
– Min’s best strategy is:
• choose the move that minimizes the score that will
result when Max chooses the maximizing move
– hence the name MiniMax
28
MINI MAX
• Restrictions:
– 2 players: MAX (computer) and MIN (opponent)
deterministic, perfect information
Select a depth-bound and evaluation function
MAX
MIN
MAX
Select
this move
3
2
2
3
1
5
3
1
4
4
3
- Construct the tree up till
the depth-bound
- Compute the evaluation
function for the leaves
- Propagate the evaluation
function upwards:
- taking minima in MIN
- taking maxima in MAX
Modified game
• From leaves upward, analyze best decision for
player at node, give node a value
6
Player 1
0
Player 2
-1
0
-1
1
Player 1
-1
1
-2
Player 2
6
0
Player 1
1
1
0
6
4
0
1
0
-3
4
-5
7
Player 1
1
0
6
7
Player 1
1
-8
Entire Search Space
Moving the scores from
the bottom to the top
Moving a score
when there’s a choice
• Use minimax assumption
– Rational choice for the player below the number you’re moving
Choosing the best move
Minimax algorithm
Properties of minimax
•
•
•
•
•
•
•
•
Complete? Yes (if tree is finite)
Optimal? Yes (against an optimal opponent)
Time complexity? O(bm)
Space complexity? O(bm) (depth-first exploration)
• For chess, b ≈ 35, m ≈100 for "reasonable" games
 exact solution completely infeasible
Multiplayer games
• Games allow more than two players
• Single minimax values become vectors
Exercise
What is value at the root?
Game Playing – Example
• Nim (a simple game)
• Start with a single pile of tokens
• At each move the player must select a pile
and divide the tokens into two non-empty,
non-equal piles
+
+
+
7
6-1
5-1-1
5-2
4-2-1
4-1-1-1
4-3
3-2-2
3-2-1-1
3-1-1-1-1
3-3-1
2-2-2-1
2-2-1-1-1
2-1-1-1-1-1
Maximilian vs. Minerva
(7,Min)
(6,1,Max)
(5,1,1,Min)
(5,2,Max)
(4,2,1,Min)
(4,1,1,1,Max)
(3,1,1,1,1,Min)
(2,1,1,1,1,1,Max)
(4,3,Max)
(3,2,2,Min)
(3,2,1,1,Max)
(3,3,1,Min)
(2,2,2,1,Max)
(2,2,1,1,1,Min)
Game tree
From M. T. Jones, Artificial Intelligence: A Systems Approach
Current board:
X’s move
Minimax algorithm: Example
From M. T. Jones, Artificial Intelligence: A Systems Approach
Current board
X’s move
Problem of minimax search
• Number of games states is exponential to
the number of moves.
– Solution: Do not examine every node
– ==> Alpha-beta pruning
• Remove branches that do not influence final decision
Alpha-beta pruning
• Basic idea: “If you have an idea that is surely
bad, don't take the time to see how truly
awful it is.” -- Pat Winston
MAX
>=2
MIN =2
• We don’t need to compute
the value at this node.
<=1
MAX
2
7
1
?
• No matter what it is, it can’t
affect the value of the root
node.
Example of Alpha-Beta Pruning
player 1
player 2
• Depth first search a good idea here
– See notes for explanation
Alpha-Beta Pruning for Player 1
1. Given a node N which can be chosen by player one,
then if there is another node, X, along any path, such
that (a) X can be chosen by player two (b) X is on a
higher level than N and (c) X has been shown to
guarantee a worse score for player one than N, then
the parent of N can be pruned.
2. Given a node N which can be chosen by player two,
then if there is a node X along any path such that (a)
player one can choose X (b) X is on a higher level than
N and (c) X has been shown to guarantee a better
score for player one than N, then the parent of N can
be pruned.
Modified game
• From leaves upward, analyze best decision for
player at node, give node a value
6
Player 1
0
Player 2
-1
0
-1
1
Player 1
-1
1
-2
Player 2
6
0
Player 1
1
1
0
6
4
0
1
0
-3
4
-5
7
Player 1
1
0
6
7
Player 1
1
-8
Alpha and Beta values
• Mx node has  value
– the alpha value is lower bound on the exact minimax score
– with best play Mx can guarantee scoring at least 
• Min node has  value
– the beta value is upper bound on the exact minimax score
– with best play Min can guarantee scoring no more than 
• At Max node, if an ancestor Min node has  < 
– Min’s best play must never let Max move to this node
• therefore this node is irrelevant
– if  = , Min can do as well without letting Max get here
• so again we need not continue
49
Alpha-Beta Pruning Rule
• Two key points:
– alpha values can never decrease
– beta values can never increase
• Search can be discontinued at a node if:
– It is a Max node and
• the alpha value is  the beta of any Min ancestor
• this is beta cutoff
– Or it is a Min node and
• the beta value is  the alpha of any Max ancestor
• this is alpha cutoff
50
Rules for Alpha-beta Pruning
• Alpha Pruning: Search can be stopped below
any MIN node having a beta value less than or
equal to the alpha value of any of its MAX
ancestors.
• Beta Pruning: Search can be stopped below
any MAX node having a alpha value greater
than or equal to the beta value of any of its
MIN ancestors.
Alpha-Beta Pruning
Summary
• Alpha = the value of the best choice we’ve
found so far for MAX (highest)
• Beta = the value of the best choice we’ve
found so far for MIN (lowest)
• When maximizing, cut off values lower than
Alpha
• When minimizing, cut off values greater
than Beta
α-β pruning example
α-β pruning example
α-β pruning example
α-β pruning example
α-β pruning example
Alpha-beta example
3
MAX
3
MIN
3
12
8
14 1 - prune
2 - prune
2
14
1
Another α-β Pruning Example
A
B
D
H
6
C
E
F
G
I
J
K
L
M
5
8
10
2
1
N
15
O
18
With alpha-beta pruning (view
presentation for animation)
Minimax with Alpha-Beta pruning
alpha=3
Max
Min
beta=3
Max
5>
beta,
so
prune
3
3
My turn
0<
alpha,
so
prune
3
No more branches,
so this is the value
2<
alpha,
so
prune
Opp turn
0
2
My turn
Min
2
3
5
0
2
1
Max
6
Min
6
A
B
C
2

6
Max
D
>=8
E
F
2
G

H
I
J
6
5
8
Computer Move
K
L
M
2
1
Opponent Move
Properties of α-β
• Pruning does not affect final result
•
• Good move ordering improves effectiveness of pruning
•
• With "perfect ordering," time complexity = O(bm/2)
 doubles depth of search
• A simple example of the value of reasoning about which
computations are relevant (a form of metareasoning)
•
Alpha-Beta Example
0 5 -3 3 3 -3 0 2 -2 3 5 2 5 -5 0 1 5 1 -3 0 -5 5 -3 3 2
Alpha-Beta Example
1
0
1
0
0
0
0
-3
2
2
2
1
3
3
1
2
2
1
-5
2
1
-5
2
-3
-5
2
0 5 -3 3 3 -3 0 2 -2 3 5 2 5 -5 0 1 5 1 -3 0 -5 5 -3 3 2
The Game
Rules:
1. Red goes first
2. On their turn, a player must move their piece
3. They must move to a neighboring square, or if their opponent is
adjacent to them, with a blank on the far side, they can hop over
them
4. The player that makes it to the far side first wins.
Game Tree Example
MIN
MAX
10 11
9
12
14 15 13 14
5
2
4
1
3
22 20 21
Stage 1
α = -∞
α = -∞
α = -∞
?
β=∞
β=∞
β=∞
α = -∞ β = ∞
10 11
9
12
14 15 13 14
5
2
4
1
3
22 20 21
Stage 1
?
α = 10
β=∞
10
α = -∞ β = 10 α = 10 β = ∞
10
10 11
9
12
14 15 13 14
5
2
4
1
3
22 20 21
Stage 2 – Shallow Pruning
α = -∞
β = 10
10
α = 10 10 β = ∞
α = -∞
β = 10
9
α = 10 β = 9 α = -∞ β = 10
10 11
9
12
14 15 13 14
5
2
4
1
3
22 20 21
Game Tree example contd.
α = 10
β=∞
10
α = -∞ 10 β = 10
14
α = 14
β = 10
14
α = -∞ β = 10
10 11
9
12
14 15 13 14
5
2
4
1
3
22 20 21
Game Tree example contd.
α = 10
β=∞
α = 10
α = 10
β=∞
β=∞
α = 10 β = ∞
10 11
9
12
14 15 13 14
5
2
4
1
3
22 20 21
Game Tree example contd.
α = 10
β=∞
5
α = 10 β = 5
10 11
9
12
14 15 13 14
5
2
α = 10 β = ∞
4
1
3
22 20 21
Game Tree example contd.
10
5
α = 10
β=5
5
α = 10
β=∞
4
α = 10 β = 4
10 11
9
12
14 15 13 14
5
2
4
1
3
22 20 21
The α-β algorithm
The α-β algorithm
Games of chance
Ex.: Blackgammon:
Form of the game tree:
Games that include chance
chance nodes
Possible moves (5-10,5-11), (5-11,19-24),(5-10,10-16) and (5- •
11,11-16)
[1,1], [6,6] chance 1/36, all other chance 1/18 •
“2/3 of the average” game
• Everyone writes down a number between 0 and 100
• Person closest to 2/3 of the average wins
• Example:
–
–
–
–
–
–
A says 50
B says 10
C says 90
Average(50, 10, 90) = 50
2/3 of average = 33.33
A is closest (|50-33.33| = 16.67), so A wins
The End
107