Download Limitation of ridge regression

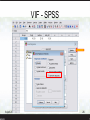
Multicollinearity
Presented by: Shahram Arsang
Isfahan University of Medical Sciences
Email: [email protected]
April 2014
2
FOCUS
•
•
•
•
Definition of Multicollinearity
Distinguish of Multicollinearity
Remedial measures of Multicollinearity
Example
6 April 2014
3
Multicollinearity
• Definition:
predictor variable are highly correlated among themselves
• Example: body fat
• potential harm of collinearity:
difficult to infer the separate influence of such explanatory
variables on the response variable.
6 April 2014
4
Problems with Multicollinearity
1.
2.
3.
4.
adding or deleting a predictor variable change the
regression coefficient.
the extra sum of square associated with a predictor
varies , depending upon which other predictor variables
are already included in the model.
the estimated SD of the regression coefficients become
large
the estimated regression coefficients individually may
not be statistically significant even though a definite
statistical relations exists between the response variable
and the set of predictor variables.
6 April 2014
5
6 April 2014
6
• diagnosis consists of two related but
separate elements:
1- detecting the presence of collinear
2-assessing the extent to which these
relationships have degraded estimated
parameters.
6 April 2014
7
diagnostic
Informal diagnostics for multicollinearity
1-large changes in the estimated regression coefficient when a
predictor variable is added or deleted, or when an observation is
altered or deleted.
2- nonsignificant result in individual tests on the regression coefficient
for important predictor variables.
3- estimated regression coefficient with an algebraic sign that is the
opposite of that expected from theoretical considerations or prior
experience.
4- large coefficient of simple correlation between pairs of predictor
variable in the correlation matrix rxx.
5- wide confidence intervals for the regression coefficients representing
important predictor variables .
6 April 2014
8
limitation of informal diagnostics
1. they provide qualitative measurements
2. sometimes the observed behavior may occur without
Multicollinearity being present.
Multicollinearity diagnostic methods
• Correlation matrix R (or
) of x`s
(absence of high correlations cannot be viewed as evidence of no problem)
•
• Variance Inflation Factor (VIF)
Weakness:
1. unable to reveal the presence of several coexisting near dependencies among
the explanatory variates.
2. meaningful boundary to distinguish between values of VIF
• The technique of Farrar and Glauber (partial
correlation)
6 April 2014
10
The technique of Farrar and
Glauber
• the n*p data matrix X is a sample of size n from
a p-variate Gaussian (normal) distribution
• that is, the partial correlation between Xi and
Xj, adjusted for all other X-variates, to
investigate the patterns of interdependence
in greater detail
6 April 2014
11
Variance inflation factor (VIF)
VIF: how much the variances of the ß are inflated as compared to when
the xi`s are not linearly related.
Variance-covariance matrix of the ß and ß*:
Diagnostic uses
severity of multicollinearity:
1. Large value of VIF
VIF > 10
2. means of the VIF
: how far the estimated standardized regression coefficient bk* are from
the true values βk*.
It can be shown that the expected value of the sum of these squared
errors (bk*-βk*)2 is given by :
When no X variable is linearly related to the others in the
regression model ;
Sum of (VIF)k ≡ p-1
Provide useful information about the effect of multicollinearity on
the sum of the squared errors :
Mean of the VIF values , to be denote by (VIF) :
VIF > 1
indicate of serious Multicollinearity problems.
Body fat example ;
The expected sum of the squared errors in the least squares
standardized regression coefficient is nearly 460 times as large
as it would be if the x variables were uncorrelated .
Multicollinearity problem ?
Comments
1. reciprocal of the VIF for exclusion x variables:
2. Limitation of VIF: distinguish between several simultaneous
multicollinearity
Remedial measures
1.
2.
3.
4.
Making predictions is not a problem
Centered data for x`s
Dropping one or more predictors
Add some cases that may break the pattern of
multicollinearity
5. Use different data sets to estimate different
coefficients
6. Principal component analysis
6 April 2014
18
Ridge regression
• By modifying the method of least square to allow
biased estimator of the regression coefficients
• Ridge estimators:
by the correlation transform
• Idea is to use a small biasing constant c and find
6 April 2014
19
Ridge regression
b R  (rxx  cI )1 ryx
•
• C
standardized ridge coefficients
amount of bias in estimator
• C=0
• c>0
=OLS in standardized form
`s are biased but more stable than OLS
6 April 2014
20
Ridge regression
• Results:
1. As c increases, bias increases, variance of the
betas decreases
2. There always exists a c for which the total
MSE for ridge regression is SMALLER than
that for OLS.
3. There are no hard and fast ways of finding c.
6 April 2014
21
• Choice of biasing constant c:
1. Ridge trace: Simultaneous plot of the values of the
(p-1) estimated ridge standardized regression
coefficients for different values of c between 0 and 1.
2. VIF
6 April 2014
22
Choice of biasing constant c
• Smallest value of c where it is deemed that:
1- regression coefficients have steadied itself and
2- VIF is small
6 April 2014
23
Comments:
•
• Limitation of ridge regression:
1-Precision of ridge regression coefficient:
Bootstrap
2- choice of c
6 April 2014
24
 Use ridge regression to reducing predictor variables:
• Unstable ridge trace with coefficient tending toward zero
• Ridge trace is stable but at a very small value
• Unstable ridge trace that do not tend toward zero: candidate
6 April 2014
25
VIF - SPSS
6 April 2014
26
Output- Spss
6 April 2014
27
Example 2 – VIF value and
remedial measure
6 April 2014
28