Download Randomized local-spin mutual exclusion

O(log n / log log n) RMRs
Randomized Mutual Exclusion
Danny Hendler
Philipp Woelfel
PODC 2009
Ben-Gurion University
University of Calgary
Talk outline





Prior art and our results
Basic Algorithm (CC)
Enhanced Algorithm (CC)
Pseudo-code
Open questions
Most Relevant Prior Art
 Best upper bound for mutual exclusion: O(log n) RMRs
(Yang and Anderson, Distributed Computing '96).
 A tight Θ(n log n) RMRs lower bound for deterministic mutex
(Attiya, Hendler and Woelfel, STOC '08)
 Compare-and-swap (CAS) is equivalent to read/write for RMR
complexity
(Golab, Hadzilacos, Hendler and Woelfel, PODC '07)
Our Results
Randomized mutual exclusion algorithms (for both CC/DSM)
that have:
 O(log N / log log N) expected RMR complexity
against a strong adversary, and
 O(log N) deterministic worst-case RMR complexity
Separation in terms of RMR complexity between
deterministic/randomized mutual exclusion algorithms
Shared-memory scheduling adversary types
 Oblivious adversary: Makes all scheduling decisions in
advance
 Weak adversary: Sees a process' coin-flip only after the
process takes the following step, can change future
scheduling based on history
 Strong adversary: Can change future scheduling after
each coin-flip / step based on history
Talk outline





Prior art and our results
Basic algorithm (CC model)
Enhanced Algorithm (CC model)
Pseudo-code
Open questions
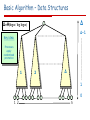
Basic Algorithm – Data Structures
Δ
Δ=Θ(log n / log log n)
Δ-1
Key idea:
Processes
apply
randomized
promotion
1
2
Δ
1
0
1 2
n
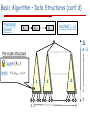
Basic Algorithm – Data Structures (cont'd)
Promotion
Queue
pi1
pi2
pik
notified[1…n]
Δ
Δ-1
Per-node structure
lock{P,}
apply: <v1,v2, …,vΔ>
1
2
Δ
1
12
n
0
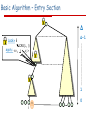
Basic Algorithm – Entry Section
Δ
Δ-1
Lock=i
CAS(, i)
apply: <v1, 
,
i …,vΔ>
1
0
i
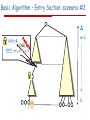
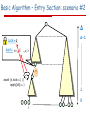
Basic Algorithm – Entry Section: scenario #2
Δ
Δ-1
Lock=q
CAS(,i)
apply: <v1, ,
i …,vΔ>
1
0
i
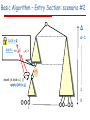
Basic Algorithm – Entry Section: scenario #2
Δ
Δ-1
Lock=q
apply: <v1, ,
i …,vΔ>
await (n.lock=) ||
apply[ch]=)
1
0
i
Basic Algorithm – Entry Section: scenario #2
Δ
Δ-1
Lock=q
apply: <v1, ,
i …,vΔ>
await (n.lock=) ||
apply[ch]=)
1
0
i
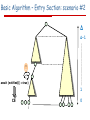
Basic Algorithm – Entry Section: scenario #2
Δ
Δ-1
await (notified[i) =true)
1
CS
0
i
Basic Algorithm – Exit Section
ClimbLock=p
up from leaf until
lastapply:
node<v
captured
q, …,vΔ>
1, 
in entry section
Δ
Δ-1
1
Lottery
0
p
Basic Algorithm – Exit Section
Δ
Perform a lottery
Lock=p

on the
root
Δ-1
apply: <v1, , …,vΔ>
Promotion
Queue
q
s
1
t
0
p
Basic Algorithm – Exit Section
t
Δ
CS
Δ-1
await (notified[i) =true)
Promotion
Queue
q
s
1
t
0
i
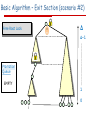
Basic Algorithm – Exit Section (scenario #2)
Δ
Free Root Lock
Δ-1
Promotion
Queue
EMPTY
1
0
i
Basic Algorithm – Properties
Lemma: mutual exclusion is satisfied
Proof intuition: when a process exits, it either
 signals a single process without releasing the root's lock, or
 if the promoted-processes queue is empty, releases the lock
o When lock is free, it is captured atomically by CAS
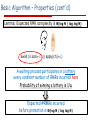
Basic Algorithm – Properties (cont'd)
Lemma: Expected RMR complexity is Θ(log N / log log N)
await (n.lock=) || apply[ch]=)
A waiting process participates in a lottery
every constant number of RMRs incurred here
Probability of winning a lottery is 1/Δ
Expected #RMRs incurred
before promotion is Θ(log N / log log N)
Basic Algorithm – Properties (cont'd)
 Mutual Exclusion
 Expected RMR complexity:Θ(log N / log log N)
 Non-optimal worst-case complexity and
(even worse) starvation possible.
Talk outline





Prior art and our results
Basic algorithm (CC)
Enhanced Algorithm (CC)
Pseudo-code
Open questions
The enhanced algorithm.
Key idea
Quit randomized algorithm after incurring ‘'too many’’ RMRS
and then execute a deterministic algorithm.
Problems
 How do we count the number of RMRs incurred?
 How do we “quit” the randomized algorithm?
Enhanced algorithm: counting RMRs problem
await (n.lock=) || apply[ch]=)
The problem: A process may incur here an unbounded
number of RMRs without being aware of it.
Counting RMRs: solution
Key idea
Perform both randomized and deterministic promotion
Lock=p
apply: <v1, q, …,vΔ>
token:
 Increment promotion token whenever releasing a node
 Perform deterministic promotion according to promotion index
in addition to randomized promotion
The enhanced algorithm: quitting problem
Upon exceeding
allowed number of
RMRs, why can't a
process simply release
captured locks and
revert to a
deterministic
algorithm?
?
1
2
Δ
12
Waiting processes may incur RMRs without
participating in lotteries!
N
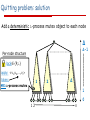
Quitting problem: solution
Add a deterministic Δ-process mutex object to each node
Δ
Δ-1
Per-node structure
lock{P,}
apply: <v1,v2, …,vΔ>
token:
1
MX: Δ-process mutex
2
Δ
1
12
n
0
Quitting problem: solution (cont'd)
Per-node structure
lock{P,}
apply: <v1,v2, …,vΔ>
token:
MX: Δ-process mutex
• After incurring O(log Δ) RMRs on a node, compete for the
MX lock. Then spin trying to capture node lock.
• In addition to randomized and deterministic promotion, an
exiting process promotes also the process that holds the
MX lock, if any.
Quitting problem: solution (cont'd)
• After incurring O(log Δ) RMRs on a node, compete for the
MX lock. Then spin trying to capture node lock.
Worst-case number of RMRs = O(Δ log Δ)=O(log n)
Talk outline





Prior art and our results
Basic algorithm (CC)
Enhanced Algorithm (CC)
Pseudo-code
Open questions
Data-structures
thei'thi'th leaf
The entry section
i'th
The exit section
i'th
Open Problems
 Is
•
•
•
this best possible?
For strong adversary?
For weak adversary?
For oblivious adversary?
 Is there an abortable randomized algorithm?
 Is there an adaptive one?