Download class10 - Duke People

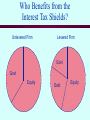
Class 10
Advanced Project
Evaluation
Two Questions
n
n
Question 1: What mix of debt and equity is
optimal for our firm?
Question 2: Given the capital structure chosen by
our firm, how can we use publicly available data
from other firms (with capital structures different
from ours) to aid in project evaluation decisions?
Perfect Capital Markets: The
MM Irrelevance Proposition
n
Assume perfect capital markets:
 No taxes or transaction costs
 No bankruptcy costs
n
Modigliani-Miller Irrelevance Proposition:
Under perfect capital markets, the firm’s capital
structure choice (i.e., mix of debt and equity) has
no effect on its total market value or its cost of
funds (i.e., the cost of financing its investments).
Proof By Arbitrage
n
n
n
n
Consider two firms with identical operating cash
flows, X, but different capital structures.
Firm U is all-equity financed (i.e., unlevered).
For an unlevered firm, VU = EU.
Firm L uses both debt and equity financing (i.e.,
levered). For a levered firm, VL=EL+DL.
We will show that because these two firms have
identical operating cash flows, they must have
identical total market values, VU = VL, despite
having different capital structures.
Proof By Arbitrage
n
n
Suppose you purchase a fraction a of the equity
of the unlevered firm. Your initial cost and
future cash flows are as follows:
Investment
Future Cash Flow
a VU
aX
For simplicity, we assume that all operating cash
flows are paid out as dividends to shareholders.
Proof By Arbitrage
n
Now suppose you bought a fraction a of the debt
and equity of the levered firm. Your initial cost
and future cash flows are as follows:
Investment
a DL
a EL
a VL
Future Cash Flow
a Min[cF,X]
a Max[0,X-cF]
aX
Proof By Arbitrage
n
n
n
Note that the future cash flows on both
investments are the same and equal to aX for all
future periods.
Since your future cash flows are the same under
both investments, the cost of the investments
must be equal to prevent arbitrage, aVU = aVL.
This result is M-M Proposition I: In a perfect
capital market, the value of the firm is invariant
to its capital structure. Hence, VU = VL.
Perfect Capital Markets:
Leverage and the Cost of Capital
Firm
Value
VU
VL
DL/EL
Perfect Capital Markets:
Leverage and the Cost of Capital
n
In a perfect capital market, the firm’s weighted
average cost of capital is calculated as follows:
F
F
E I
D I
 r G J r G J
HV K HV K
L
L
*
r
n
L
e
L
L
d
L
Modigliani-Miller Proposition II: In a perfect
capital market, the firm’s weighted average cost
of capital is invariant to its capital structure.
Hence, r*L = r*U.
Perfect Capital Markets:
Leverage and the Cost of Capital
Cost of
Capital
r *U
r *L
DL/EL
Perfect Capital Markets:
Leverage and the Cost of Capital
n
The WACC formula implies the following
relationship between the firm’s cost of equity and
its leverage:
r r
L
e
n
L
*
F
D I
c
r r h
G
J
HE K
L
L
*
d
L
In a perfect capital market, r*L = r*U =reU. This
represents a return to compensate investors for the
inherent business risk of the assets of the firm.
Perfect Capital Markets:
Leverage and the Cost of Capital
n
n
In addition to this business risk, there is a leverage
effect. The equityholders in the levered firm
demand a higher return to compensate them for the
fact that there are debtholders lined up in front of
them with a prior claim over the assets of the firm.
As leverage increases two things happen:
 the equityholders demand higher returns.
 we finance more projects by (relatively cheaper) debt.
n
In a perfect capital market, these two effects
cancel exactly.
Perfect Capital Markets:
Leverage and the Cost of Capital
Required
Return
rLe
rUe= rU* =rL*
rLd
DL/EL
Perfect Capital Markets:
Leverage and the Cost of Capital
n
The CAPM can be used to compute all of
these discount rates:
 Use the equity beta to compute the return on
equity: E[reL] = rf + beL (E[rm]- rf).
 Use the debt beta to compute the return on debt:
E[rd] = rf + bd (E[rm]- rf).
 Use the asset beta to compute a return
commensurate with the business risk of the
assets: E[reU] = rf + beU (E[rm]- rf).
Perfect Capital Markets:
Leverage and the Cost of Capital
n
n
Note that the beta of equity in an unlevered
firm (beU) is also known as the beta of the
assets (ba) since the unlevered firm has no
leverage effect.
The only source of risk in the unlevered
firm is the inherent business risk of the
assets themselves.
Perfect Capital Markets:
Leverage and the Cost of Capital
n
The firm’s asset beta is a weighted average of the
debt and equity betas:
ba  b
n
F
F
D I
E I
b G J
G
J
HV K HV K
L
L
d
L
L
L
e
L
This implies the following relationship between
the firm’s equity beta and its leverage:
c
b  ba  ba  b
L
e
F
D I
hG
J
HE K
L
L
d
L
Perfect Capital Markets Example
n
An unlevered firm has 10 million shares outstanding, each with a market price of $20 and a
beta of 1.0. The firm is considering issuing $50
million of 10% debt and using the proceeds to pay
a dividend to shareholders. What effect will this
capital structure change have on the value of the
firm, the WACC, the equity beta, the required
return on equity, and the wealth of the firm’s
shareholders? Assume a riskfree interest rate of rf
= 6.0% and a market risk premium of [E(rM)-rf] =
8.0%.
Perfect Capital Markets Example
n
n
n
Value of the Unlevered Firm:
VU = 10(20) = 200 million.
Cost of Capital for the Unlevered Firm:
E[reU] = rf + beU (E[rm]- rf).
E[reU] = 0.06 + 1.0 (0.08) = 0.14.
Since the firm is unlevered, the value of equity
and cost of equity are the same as for the firm as
a whole.
Perfect Capital Markets Example
n
In perfect capital markets, VL = VU and r*L = r*U.
 VL = VU = $200 million
 r*L = r*U = 14.0%
n
Since the cost of debt is 10.0%, the cost of equity
is determined as follows:
reL = reU + [reU -rd ](D/E)
reL = 0.14 + [0.14 - 0.10 ](50/150) = 0.1533.
Perfect Capital Markets Example
n
n
The equity beta can be determined from the
CAPM as follows:
E[reL] = rf + beL (E[rm]- rf).
0.1533 = 0.06 + beL (0.08).
beL = 1.167.
The wealth of the firm’s shareholders has not
changed.
Shareholder Wealth = Share Value + Dividend
= $150 + $50 = $200 million
The Effect of Leverage
with Corporate Taxes
n
n
n
Now assume that corporations pay taxes at the
rate of t. We continue to assume that bankruptcy
costs are zero.
Consider two identical firms: one levered the
other unlevered. Both firms produce earnings
before interest and taxes of X per year in
perpetuity.
What are the yearly cash flows to debt and equity
of these two firms? What are the market values
of these two firms?
The Effect of Leverage
with Corportate Taxes
n
The yearly after-tax cash flows are given below:
Levered Firm
EBIT
Less: Interest
Less: Taxes
Total to Equity
Total to Debt
Total Cash Flow
X
Unlevered
Firm
X
-cF
0
-t(X-cF)
-tX
(X-cF)(1-t)
X(1-t)
cF
0
X(1-t) + tcF
X(1-t)
The Effect of Leverage
with Corporate Taxes
n
n
The yearly after-tax cash flows to a levered firm
are equal to those for the unlevered firm, plus the
tax shield on interest.
The value of the levered firm will thus be equal to
the following:
VL = VU + PV(ITS)
T
V V  
L
U
t 1
tcF
b1  r g
t
d
The Effect of Leverage
with Corporate Taxes
n
Assuming debt is perpetual, we have:
V V 
L
n
n
U
tcF
rd
 V  tD
U
The fact that the firm increases its value by using
debt implies that the optimal capital structure for
the firm is 99.99% debt.
The tax deductibility of interest was one of the
driving forces behind the LBO wave of the
The Relationship Between
Firm Value and Leverage
Total Firm
Value
VL
Present Value of
Interest Tax Shields
VU
Value of
Unlevered
Firm
D/E
Who Benefits from the
Interest Tax Shields?
n
Consider the unlevered firm from our previous
example. The firm currently has 10 million
shares outstanding, each with a market price of
$20 per share. The firm is considering issuing
$50 million in 10% debt. Assume that this debt
is perpetual and that the firm’s tax rate is 34%.
How does this capital structure change affect the
value of the firm and the wealth of the firm’s
shareholders?
Who Benefits from the
Interest Tax Shields?
n
n
Since the debt is perpetual, the value of the firm
will increase as follows:
VL = VU +tD
VL = 200 +(0.34)(50) = 217 million.
Since the debt is issued at fair market value, the
value of equity after the capital structure change
is:
Equity Value = $217 - $50 = $167 million.
Who Benefits from the
Interest Tax Shields?
n
Since the proceeds from the debt issue are used
to pay a dividend to shareholders, their wealth
increases by $17 million. This is the value of the
interest tax shields on debt.
Shareholder Wealth = Share Value + Dividend
= $167 + $50 = $217 million
n
If equityholders benefit, who loses?
Who Benefits from the
Interest Tax Shields?
Unlevered Firm
Levered Firm
Govt
Govt
Equity
Debt
Equity
The Effect of Corporate Taxes and
Leverage on the Cost of Capital
n
With corporate taxes, the firm’s weighted
average cost of capital is calculated as follows:
F
F
E I
D I
 r G J r b
1 t g
G
J
HV K
HV K
L
L
*
r
n
L
e
L
L
d
L
Modigliani and Miller have shown that with
perpetual debt, the WACC formula can be
rewritten as follows:
r r
L
*
U
*
L
F
D IO
1  t G JP
M
N HV KQ
L
L
Leverage and the Cost of Capital
with Corporate Taxes
Cost of
Capital
r *U
r *L
DL/EL
The Effect of Corporate Taxes and
Leverage on the Cost of Capital
n
The WACC formula can be rewritten to give the
following expression for the cost of equity:
r r
L
e
n
F
D I
c
r r h
b1  t gG
J
HE K
L
U
*
U
*
d
L
Using the CAPM, we can derive an expression
for the firm’s equity beta:
b b
L
e
F
D I
c
b b h
b1  t gG
J
HE K
L
U
e
U
e
d
L
Three Effects
n
In determining the risk (beta) and return
from holding equity in a levered firm, there
are three effects to consider:
 The inherent business risk of the assets the
firm has invested in.
 The leverage effect whereby equityholders
demand a higher return in compensation for
taking a residual claim.
 The tax subsidy effect whereby the govt
contributes to interest payments on debt.
The Effect of Corporate Taxes and
Leverage on the Cost of Capital
n
Rearranging the previous equation gives us an
equation for the firm’s asset beta:
ba  b
n
F
I
F
I
E
D
b b
1 t g
G
J
G
J
V  tD K
V  tD K
H
H
L
L
e
L
L
L
d
L
L
The asset beta reflects just the inherent business
risk of the assets of the firm. That is, we have
purged the equity beta of the leverage and tax
subsidy effects.
Leverage and the Cost of Capital
n
Consider once again the firm from our previous
example. The firm has a total market value of
$217 million, consisting of $50 million in 10%
debt and $167 million in equity. The firm’s
unlevered (asset) beta is 1.0. Assuming that the
firm faces a tax rate of 34%, what is the
WACC, equity beta, and cost of equity for the
firm?
Leverage and the Cost of Capital
n
The firm’s new WACC can be determined from its
unlevered cost of capital according to the formula:
L
F
D IO
50 IO
L
F
r r M
1 t G J
 014
. M
1  0.34G J
 0129
.
P
P
H
K
V
217
H
K
N
Q
N
Q
The firm’s cost of equity is:
F
D I
r  r c
r r h
b1  t gG
J
HE K
50 I
F
r  014
. b
014
.  010
. g
 01479
.
b1  0.34gG
J
H167 K
L
L
*
U
*
L
n
L
L
e
L
e
U
*
U
*
d
L
Leverage and the Cost of Capital
The firm’s equity beta can be determined by the
CAPM:
E[reL] = rf + beL (E[rm]- rf).
0.1479 = 0.06 + beL (0.08).
beL = 1.099.
To verify the WACC calculation, lets compute it
directly using the textbook formula:
n
n
L
*
r
167 I
50 I
F
F
 01479
.
 010
. b
1  0.34g
 0129
.
G
J
G
J
H217 K
H217 K
Example 1
n
Suppose your firm has identified a potential
investment project. The investment project
requires you to make an initial outlay of $50
million and is expected to return after-tax cash
flows of $8 million per year for the indefinite
future. The project has an asset beta of 1.2 and
supports $20 million in additional debt capacity.
Use the appropriate discount rate to find the
project’s NPV. Assume a riskfree rate of 6%, a
market risk premium of 8%, and a tax rate of 34%.
Example 1
n
Unlevered Cost of Capital
r*U = 0.06 + 1.2(0.08)=0.156.
n
Present Value of After-Tax Cash Flows
$8.0
PV ( CF ) 
 $51.282million
.156
n
Present Value of Interest Tax Shields
PV ( ITS )  tD .34 ($20)  $6.8million
Example 1
n
WACC Calculation
L
D
r*L  r*U 1  t
VL
n
NPV Calculation
L
O
F
I
M
P
G
J
N H KQ
20 IO
L
F
 0156
. M
1  0.34G J
 01377
.
P
N H58.8KQ
$8.0
NPV 
 $50  $8.08million
.1377
General Principles
n
n
n
n
Each investment project has its own cost of capital
that depends upon the risk of the investment.
The risk of the investment project depends upon its
unlevered (asset) beta.
The unlevered cost of capital can be estimated
using the CAPM.
The project’s leverage ratio should depend upon its
own debt capacity, not on the particular source of
funds used to finance the project.
Accounting for Leverage
in Capital Budgeting
n
n
n
Suppose your firm is considering an investment
in a project different from the firm’s core
operations.
NPV must be computed using a discount rate
appropriate for the project, not the firm.
How do we find this?
 Step 1: Compute the beta of the assets by unlevering
another firm’s equity beta.
Accounting for Leverage
in Capital Budgeting
 Step 2: Use the CAPM to determine a required return
to compensate investors for bearing this inherent
business risk.
 Step 3: Adjust this required return to incorporate the
leverage and tax subsidy effects associated with this
project.
 Step 4: Use this required return to find the NPV.
Capital Budgeting Example
n
Your firm is currently in the computer software
business, but is considering investing in the
development of a new airline. Information on your
firm and the airline industry are given below:
Your
Firm
1.20
Airline
Industry
1.95
Debt-Equity Ratio
0
67%
Ave. Cost of Debt
-
10%
Equity Beta
Capital Budgeting Example
n
n
n
Your airline project is expected to cost $20
million per year for the next 5 years and is
expected to generate after-tax cash flows of $10
million per year indefinitely thereafter.
Because of your firm’s current debt position, you
will finance the airline project with 50% debt,
even though this is less than standard for airline
projects.
The corporate tax rate is 34%, the riskfree interest
rate is 9%, and the market risk premium is 8%.
Capital Budgeting Example
n
Step 1: Unlever Equity Beta for Airlines
ba  b
ba
F
I
F
I
E
D
b b
1 t g
G
J
G
J
V  tD K
V  tD K
H
H
L
L
e
L
L
L
d
L
0.6
0.4
F
I
F
I
 195
. G
 0125
. b
1  0.34g
J
G
J
H1  (0.34)0.4 K
H1  (0.34)0.4 K
 139
.
n
L
The debt beta, bD comes from the CAPM:
rd  010
.  0.09  b d 0.08
b d  0125
.
b g
Capital Budgeting Example
n
Step 2: Calculate the Unlevered Cost of Capital
b g
r  0.09  139
. 0.08  0.2012
U
*
n
Step 3: Calculate the Levered Cost of Capital
L
F
D IO
r M
1  t G JP
N HV KQ
0.4 IO
L
F
 0.2012 M
1  0.34G JP
 01738
.
N H1 KQ
L
r*L
U
*
L
Capital Budgeting Example
n
Step 4: Calculate the NPV of the Project

5
$10
$20
NPV  

 37.61million
t
t
.
)
.
)
t  6 (11738
t 1 (11738
Factors that Influence Debt
Policy in Practice
n
n
n
n
n
n
n
Tax Position of the Corporation
Costs of Bankruptcy and Financial Distress
Variability of the Firm’s Earnings and Cash
Flows
Asset Type: Tangible vs. Intangible Assets
Investment (or Growth) Opportunities
The Need for Financial and Operating Flexibility
Informational Asymmetries
Tax Shield-Bankruptcy Cost
Tradeoff
Firm
Value
VU+PV(ITS)
Bankruptcy
Costs
VL
VU
Value of
Unlevered
Firm
(D/E)*
D/E