* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download i+1
Mathematics of radio engineering wikipedia , lookup
Georg Cantor's first set theory article wikipedia , lookup
List of prime numbers wikipedia , lookup
Large numbers wikipedia , lookup
Infinite monkey theorem wikipedia , lookup
Collatz conjecture wikipedia , lookup
Central limit theorem wikipedia , lookup
Elementary mathematics wikipedia , lookup
Quadratic reciprocity wikipedia , lookup
Proofs of Fermat's little theorem wikipedia , lookup
Index of cryptography articles wikipedia , lookup
Stream cipher diagram
+
Recall: One-time pad in Chap. 2
+
Advantage of stream cipher
With proper design of PRNG, stream cipher is as
secure as block cipher of comparable key length (?)
Stream cipher is faster than block cipher
Disadvantage of stream cipher
never reuse the same key
c.f. you can reuse keys in block cipher
Ciphertext 1 = plaintext 1 keystream
Ciphertext 2 = plaintext 2 keystream
Ciphertext 1 Ciphertext 2
= (plaintext 1 keystream) (plaintext 2 keystream)
= plaintext 1 plaintext 2
If plaintexts are text string, credit card no., or other
streams with known properties, then cryptanalysis
may be successful. ?[DAWS96]
Random Numbers
many uses of random numbers in cryptography
keystream for a one-time pad
nonces in authentication protocols to prevent replay
session keys
public key generation
Requirement for a sequence of random numbers:
Randomness
Uniform distribution: freq. of occurrence of each number
should be approximately the same
Independence: no one value in the seq. can be inferred from
the others
Unpredictability
cannot infer future sequence on previous values
Application: randomization
Goal: determine if a given number N is
prime
Brute-force search: divide N by odd integers
less than N => N tests
N=10150
=> 10150
Randomization: test using a (sufficiently long)
sequence of randomly chosen integers
Source of random numbers:
1. Natural Random Noise
best source is natural randomness in real world
find a regular but random event and monitor
do generally need special h/w to do this
eg. radiation counters, radio noise, audio noise, thermal
noise in diodes, leaky capacitors, mercury discharge
tubes etc
starting to see such h/w in new CPU's
problems of bias or uneven distribution in signal
have to compensate for this when sample and use
best to only use a few noisiest bits from each sample
2. Published Sources
a few published collections of random numbers
Rand Co, in 1955, published 1 million numbers
generated using an electronic roulette wheel
has been used in some cipher designs cf Khafre
earlier Tippett in 1927 published a collection
issues are that:
these are limited
too well-known for most uses
3. Pseudorandom Number
Generators (PRNGs)
algorithmic technique to create “random
numbers”
deterministic algorithm
although not truly random
can pass many tests of “randomness”
Linear Congruential
Generator
common iterative technique using:
Xn+1 = (aXn + c) mod m
X0: initial seed
How to choose suitable values of parameters ?
a=1, c=1
a=7, c=0, m=32, X0=1
{1, 7, 17, 23, 1, …}
Congruence: Integers Modulo 7
Example
...
-21 -20 -19 -18 -17 -16 -15
-14 -13 -12 -11 -10 -9 -8
-7 -6 -5 -4 -3 -2 -1
0
1
2
3
4
5
6
7
8
9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31 32 33 34
...
Z7: residue class
modulo n
congruence 一致(from Gauss)
Integers a and b are congruence modulo n : a ≡ b mod n
Linear Congruential
Generator (cont.)
Xn+1 = (aXn + c) mod m
Suitable criteria to have are:
1. function generates a full-period {1,…, m-1}
2. generated sequence should appear random
3. efficient implementation (eg. with 32-bit arithmetic)
To satisfy
1. c=0, m is a prime, and certain a (?)
3. For 32-bit arithmetic, m = 232 – 1 (prime?)
Xn+1 = (aXn) mod (232 - 1)
2. Few a satisfy random: ex. a=75 =16807
Primitive root
Attacks on linear congruential
method
All parameters are known
A single number is discovered, subsequent
numbers are known
Only know the linear congruential method
Know a small sequence of numbers
X0
X1 = (aX0 + c) mod m
X2 = (aX1 + c) mod m
X3 = (aX2 + c) mod m
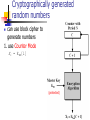
Cryptographically generated
random numbers
can use block cipher to
generate numbers
1. use Counter Mode
Xi = EKm[i]
(protected)
Cryptographically generated
random numbers (cont.)
2. use Output Feedback Mode
Xi = EKm[Xi-1]
Looks like RC4 stream cipher
Cryptographically generated
random numbers (cont.)
3. ANSI X9.17 PRNG
(one of the strongest PRNGs)
uses date-time + seed inputs and 3 triple-DES
encryptions to generate new seed & random
(triple-DES keys)
(date/time)
(next seed)
(seed)
(random output)
Blum Blum Shub (BBS) random
bit generator
based on public key algorithms
use least significant bit from iterative equation:
xi+1 = xi2 mod n
Bi+1 = xi+1 mod 2
where n=p•q, and primes p,q=3 mod 4
n=192649
=383x503
Blum Blum Shub (BBS) random
bit generator (cont.)
unpredictable, passes next-bit test
(prediction based on previous k bits)
security rests on difficulty of factoring n
is unpredictable given any run of bits
slow, since very large numbers must be used
too slow for cipher use, good for key generation


















![Problem Set 3 [Word]](http://s1.studyres.com/store/data/019170310_1-579dc2e4bff01e038f7e8fb41a8fb2e8-150x150.png)









