Download Lecture 1

Econ 805
Advanced Micro Theory 1
Dan Quint
Fall 2007
Lecture 1 – Sept 4 2007
I’m Dan Quint, welcome to Econ 805
 You are…
 Class website

http://www.ssc.wisc.edu/~dquint/econ805
 Syllabus online, with links to papers
 Lectures (no class next Thursday)
 Office hours

Mondays 11-12, Wednesdays 10-11, other times by
appointment
 Grading

Problem sets (35%), final exam (65%). Midterm?
 Readings

I’ll try to highlight which are most important
1
This class will be about auction theory














Popular auction formats
Independent private values and revenue equivalence
The mechanism design approach, optimal auctions
The “marginal revenue” analogy, reserve prices
Risk averse buyers or sellers
Auctions with strong and weak bidders
Interdependent values
Pure common values, symmetry in asymmetric auctions
Endogenous information acquisition
Endogenous entry
Collusion, shill bidding
Sequential auctions
Multi-unit auctions
Other topics
2
Today
 Why study auctions?
 Review of Bayesian games and Bayesian Nash
Equilibrium
3
Why study auctions?
4
A whole lot of money at stake…
 Christie’s and Sotheby’s art auctions – $ billions annually
 Auctions for rights to natural resources (timber, oil, natural
gas), government procurement, electricity markets
 eBay: $52 Billion worth of goods traded in 2006

eBay itself had $6 Bn in 2006 revenues, current market cap. of $46 Bn
 European 3G spectrum auctions raised over $100 Bn in 20002001; upcoming U.S. FCC auction expected to raise $20 Bn
 U.S. treasury holds auctions for $4 TRILLION in securities
annually
 “Dark pools” gaining share of trade in U.S. stocks
5
…and outcomes may be very sensitive
to the details of the auction
 One of our first results will be revenue equivalence…
 …but this fails under a wide variety of conditions
 Yahoo! vs. Google
 Adjusting for the size of each market, revenues in
European 3G auctions varied widely
Over 600 € per capita in the UK and Germany
 20 € per capita in Switzerland later the same year
 Rules in Swiss auction discouraged marginal bidders/new
entrants from participating, allowed for easy collusion
among the primary competitors

6
Auctions can be seen as a useful
microcosm for bigger markets
 “Rules of the game” and price formation are explicit,
allowing for theoretical analysis
 Most relevant data can be captured, allowing sharp
empirical work
 Auctions lend themselves to lab experiments
 Results on auctions may offer insight (or intuition)
into behavior in less structured markets
7
Insights from auction theory may be
valuable in other areas
 P. Klemperer, “Why Every Economist Should Learn
Some Auction Theory”: analogies in








Comparison of different litigation systems
“All-pay” tournaments such as lobbying, political campaigns,
patent races, and some oligopoly situations
Market frenzies and crashes
Online auto sales versus dealerships
Monopoly pricing and price discrimination
Rationing of output
Patent races
Value of new customers under oligopoly
8
And finally,
 Auction theory gives us a platform to introduce a
number of important mathematical tools/techniques

Envelope theorem

Supermodularity and monotone comparative statics

Constraint simplification (necessary and sufficient
conditions for equilibrium strategies)
9
But with all that said…
 Auctions have been a hot topic in micro theory for
over 25 years
 Basic theory of single-unit auctions is pretty well
developed
 Multi-unit auctions are less well understood

Very difficult theoretically
 Some partial results, experimental results
10
Quick Review of
Game Theory and
Bayesian Games
11
Games of complete information
 A static (simultaneous-move) game is defined by:

Players
 Action spaces
 Payoff functions
1, 2, …, N
A1, A2, …, AN
ui : A1 x … x AN  R
all of which are assumed to be common knowledge
 In dynamic games, we talk about specifying “timing,”
but what we mean is information

What each player knows at the time he moves
 Typically represented in “extensive form” (game tree)
12
Solution concepts for games of
complete information
 Pure-strategy Nash equilibrium: s  A1 x … x AN s.t.
ui(si,s-i)  ui(s’i,s-i)
for all s’i  Ai
for all i  {1, 2, …, N}
 In dynamic games, we typically focus on Subgame
Perfect equilibria

Profiles where Nash equilibria are also played within each
branch of the game tree
 Often solvable by backward induction
13
Games of incomplete information
 Example: Cournot competition between two firms,
inverse demand is P = 100 – Q1 – Q2
 Firm 1 has a cost per unit of 25, but doesn’t know
whether firm 2’s cost per unit is 20 or 30
 What to do when a player’s payoff function is not
common knowledge?
14
John Harsanyi’s big idea
(“Games with Incomplete Information Played By Bayesian Players”)
 Transform a game of
incomplete information
into a game of imperfect
information – parameters of
game are common
knowledge, but not all
players’ moves are observed
“Nature”
make 2 weak
make 2 strong
Firm 2
Firm 2
Q2
Q2

Introduce a new player,
“nature,” who determines
firm 2’s marginal cost
 Nature randomizes; firm 2
observes nature’s move
 Firm 1 doesn’t observe
nature’s move, so doesn’t
know firm 2’s “type”
Firm 1
Q1
Q1
u1 = Q1(100 - Q1 - Q2 - 25)
u1 = Q1(100 - Q1 - Q2 - 25)
u2 = Q2(100 - Q1 - Q2 - 30)
u2 = Q2(100 - Q1 - Q2 - 20)
15
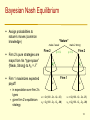
Bayesian Nash Equilibrium
 Assign probabilities to
nature’s moves (common
knowledge)
 Firm 2’s pure strategies are
maps from his “type space”
{Weak, Strong} to A2 = R+
 Firm 1 maximizes expected
payoff


in expectation over firm 2’s
types
given firm 2’s equilibrium
strategy
“Nature”
make 2 weak
Firm 2
make 2 strong
p=½
p=½
Q2W
Firm 2
Q2S
Firm 1
Q1
Q1
u1 = Q1(100 - Q1 - Q2 - 25)
u1 = Q1(100 - Q1 - Q2 - 25)
u2 = Q2(100 - Q1 - Q2 - 30)
u2 = Q2(100 - Q1 - Q2 - 20)
16
Other players’ types can enter into a
player’s payoff function
 In the Cournot example, this isn’t the case

Firm 2’s type affects his action, but doesn’t directly affect
firm 1’s profit
 In some games, it would

Poker: you don’t know what cards your opponent has, but
they affect both how he’ll plays the hand and whether you’ll
win at showdown
 Either way, in BNE, simply maximize expected payoff
given opponent’s strategy and type distribution
17
Formally, for N = 2 and finite,
independent types…
 A static Bayesian game is

A set of players 1, 2
 A set of possible types T1 = {t11, t12, …, t1K} and T2 = {t21, t22, …, t2K’} for
each player, and a probability for each type {p11, …, p1K, p21, …, p2K’}
 A set of possible actions Ai for each player
 A payoff function mapping actions and types to payoffs for each player
ui : A1 x A2 x T1 x T2  R
 A pure-strategy Bayesian Nash Equilibrium is a mapping si : Ti  Ai
for each player, such that

t kj T j
p kj ui si (ti ), s j (t kj ), ti , t kj   t T p kj ui ai , s j (t kj ), ti , t kj 
k
j
j
for each potential deviation ai  Ai
for every type ti  Ti
for each player i  {1,2}
18
Ex-post versus ex-ante formulations
 With a finite number of types, the following are equivalent:

The action si(ti) maximizes “ex-post expected payoffs” for each
type ti
Et j T j ui si (ti ), s j (t j ), ti , t j  Et j T j ui ai , s j (t j ), ti , t j





The mapping si : Ti  Ai maximizes “ex-ante expected payoffs”
among all such mappings
Eti Ti ,t j T j ui si (ti ), s j (t j ), ti , t j  Eti Ti ,t j T j ui si ' (ti ), s j (t j ), ti , t j




 I prefer the ex-post formulation for two reasons


With a continuum of types, the equivalence breaks down, since
deviating to a worse action at a particular type would not change
ex-ante expected payoffs
Ex-post optimality is almost always simpler to verify
19
Going back to our Cournot example,
with p = ½ that firm 2 is strong…
 Strong firm 2 best-responds by choosing
Q2S = arg maxq q(100-Q1-q-20)
Maximization gives Q2S = (80-Q1)/2
 Weak firm 2 sets
Q2W = arg maxq q(100-Q1-q-30)
giving Q2W = (70-Q1)/2
 Firm 1 maximizes expected profits:
Q1 = arg maxq ½q(100-q-Q2S-25) + ½q(100-q-Q2W-25)
giving Q1 = (75 – Q2W/2 – Q2S/2)/2
 Solving these simultaneously gives equilibrium strategies:
Q1 = 25, (Q2W, Q2S) = (22½ , 27½)
20
Auctions are typically modeled as
Bayesian games
 Players don’t know how badly the other bidders want
the object

Assume nature gives each bidder a valuation for the object
(or information about it) from some ex-ante probability
distribution that is common knowledge
 In BNE, each bidder maximizes his expected payoffs,
given

the type distributions of his opponents
 the equilibrium bidding strategies of his opponents
 Thursday: some common auction formats and the
baseline model
21