* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download The Foundations
Fuzzy logic wikipedia , lookup
Abductive reasoning wikipedia , lookup
Structure (mathematical logic) wikipedia , lookup
Meaning (philosophy of language) wikipedia , lookup
Axiom of reducibility wikipedia , lookup
History of logic wikipedia , lookup
Modal logic wikipedia , lookup
Mathematical proof wikipedia , lookup
Mathematical logic wikipedia , lookup
History of the function concept wikipedia , lookup
Analytic–synthetic distinction wikipedia , lookup
Boolean satisfiability problem wikipedia , lookup
Curry–Howard correspondence wikipedia , lookup
First-order logic wikipedia , lookup
Sequent calculus wikipedia , lookup
Quantum logic wikipedia , lookup
Foundations of mathematics wikipedia , lookup
Combinatory logic wikipedia , lookup
Intuitionistic logic wikipedia , lookup
Laws of Form wikipedia , lookup
Natural deduction wikipedia , lookup
Truth-bearer wikipedia , lookup
Law of thought wikipedia , lookup
Propositional formula wikipedia , lookup
Discrete Mathematics
Chapter 1.
The Foundations:
Logic and Proofs
Cheng-Chia Chen
Transparency No. 1-0
The Foundations
1. The foundations : logic and proofs
Logic and proofs:
The basis of all mathematical reasoning
has practical applications to the design of
computing machine
give the precise meaning of math. statements.
Transparency No. 1-2
The Foundations
Foundations of Logic (§§1.1-1.4)
Mathematical Logic is a tool for working with
complicated compound statements.
It includes:
A language(Vocabulary) for expressing them.
A concise notation(Syntax) for writing them.
A methodology for objectively reasoning about
their truth or falsity (Semantics and Axiomatics).
It is the foundation for expressing formal proofs
in all branches of mathematics.
Transparency No. 1-3
The Foundations
Foundations of Logic: Overview
Propositional logic (§1.1-1.2):
Basic definitions. (§1.1)
Equivalence rules & derivations. (§1.2)
Predicate logic (§1.3-1.4)
Predicates.
Quantified predicate expressions.
Equivalences & derivations.
Transparency No. 1-4
The Foundations
§1.1 Propositional Logic
Propositional Logic is the logic of compound
statements built from simpler statements
using so-called Boolean connectives.
Some applications in computer science:
Design of digital electronic circuits.
Expressing conditions in programs.
George Boole
Queries to databases & search engines. (1815-1864)
Transparency No. 1-5
The Foundations
Proposition
Proposition: A statement that is either true
or false (,but not both)
even if we do not know it is true or false now.
Example:
1. Taipei is the capital of ROC. 2. Tokyo is the capital of Korea.
3. 1+1 = 2. 4. 2+2 = 3.
5. There is no integer x,y,z and n > 2 s.t.
xn + yn = zn ---- Fermat’s last theorem
6. “Every even number > 2 is the sum of two prime numbers.”
---Goldbach’s conjecture (1742)
==>
1. Statement (1)~(6) are propositions,
2. (1),(3) are true; (2),(4) are false.
3. Nobody knew (5) is true or false until 1994, but it must be
true or false, hence it is a proposition. (6) open problem.
Transparency No. 1-6
The Foundations
More Examples
Examples:
1. What time is it? (interrogative)
2. Read this carefully! (command)
3. x+1 = 2.
4. x+y = z.
5. 李登輝是中華民國總統
==>
1. (1) and (2) are not statements
2. (3),(4) are not propositions:
neither true nor false!
3. How about (5) ?
Transparency No. 1-7
The Foundations
Propositional variables and propositional constants
In algebra, we use variables to denote an item with
unspecified value.
e.g. 10 chickens and rabbits in a cage with 26 feet. ==>
#rabbits = ? and #chickens=?
==> let x = #rabbits, y = #chickens
==> x + y = 10 /\ 2x + 4y = 26.
Likewise, In logic, we can use propositional variable
to denote an arbitrary proposition with unspecified
truth value.
e.g., If it is raining, the ground is wet. since the ground is
wet, it is raining now.
==> Let p =def “It is raining”, q =def “the ground is wet”
==> ((p ->q) /\ q) -> p.
Propositional constants(literals): only two values:
T(true), F(false).
Transparency No. 1-8
The Foundations
Operators / Connectives
Topic #1.0 – Propositional Logic: Operators
An operator or connective combines one or
more operand expressions into a larger
expression. (E.g., “+” in numeric exprs.)
Unary operators take 1 operand (e.g., −3);
Binary operators take 2 operands (eg 3
4).
ternary: p? a:b In C and Java
Propositional or Boolean operators
operate on propositions or truth values
instead of on numbers.
Transparency No. 1-9
The Foundations
Some Popular Boolean Operators
Formal Name
Nickname Arity
Symbol
Negation operator
NOT
Unary
¬ (~)
Conjunction operator AND
Binary
Disjunction operator
OR
Binary
Exclusive-OR
operator
Implication operator
XOR
Binary
IMPLIES
Binary
Biconditional
operator
IFF
Binary
↔
Transparency No. 1-10
The Foundations
Forming Compound propositions from simpler ones
using logical connectives
Primitive (or atomic) propositions:
propositional variables
propositional constants
P, Q: two known propositions
Then the followings are also propositions:
1. “P and Q” : ( P /\ Q) conjunction of P and Q
2. “It is not the case that p”: (~P) negation of P
3. “P or Q” : (P \/ Q) disjunction of P and Q
4. “P implies Q” : ( P Q) implication
P : antecedent, premise, hypotheses;
Q: consequence, conclusion
equivalent phrase:
– “P entails Q”, “Q if P”, “P only if Q”
5. “P iff Q” (P ↔ Q) equivalence of P and Q
Transparency No. 1-11
The Foundations
Truth conditions for compound propositions
1.
2.
3.
4.
5.
P /\ Q is true iff both P and Q are true
P \/ Q is true iff either P or Q is true
~P is true iff P is not true (i.e., false)
P ↔ Q is true iff both are true or both are false.
PQ is true iff whenever P is true, Q is true
( i.e., it is not the case that P is true but Q is false )
In the propositions, /\, \/, ↔ and are called binary
connectives(or operations) and ~ is called unary
connective(or operations).
Other binary connectives are possible.
What about the truth condition for primitive
propositions?
Transparency No. 1-12
The Foundations
From natural language statements to formal logic expressions
Natural language statement
Today is Friday
I have a test today
It is not the case that today is
Friday
Today is not Friday
Today is Friday and
I have a test today
If today is Friday, then I have
a test today.
Today is Friday or I have a
test today.
symbolized logic expr.
p
q
~p
~p
(P ∧ q)
(pq)
(P ∨ q)
Transparency No. 1-13
The Foundations
Truth conditions for propositions
Problem: when will you say that the sentence:
It_is_raining
is true ?
=> The proposition:” It_is_raining” is true if the meaning
(or fact) that the proposition is intended to represent
occurs(happens, exists) in the situation which the
proposition is intended to describe.
=>Example: Since it is not raining now(the current situation), the
statement It_is_raining is false (in the current situation). But if
it were raining now, then I would say that It_is_raining is true.
Factors affecting the truth value of a proposition:
the situation in which the proposition is used.
the meaning of the proposition.
Transparency No. 1-14
The Foundations
Truth table
•The meaning of logical connectives can also be
represented by a truth table.
A
B
~A
A/\B
A\/B
A->B
A<->B
0
0
1
0
0
1
1
0
1
1
0
1
1
0
1
0
0
0
1
0
0
1
1
0
1
1
1
1
Transparency No. 1-15
The Foundations
Other usual connectives
Besides /\,\/, and <->, there are also some other
connectives which you will study in digital
system.
xor , nand, nor.
Rules: let I(x) denote the truth value of x.
I(A B)=def I(~(A<->B)) [ = 1 iff not I(A)=I(B) ]
I(A nand B) =def I(~(A/\B)).
I(A nor B) =def I(~( A \/B)).
Transparency No. 1-16
The Foundations
Nested Propositional Expressions
Use parentheses to group subexpressions:
“I just saw my old friend, and either he’s
grown or I’ve shrunk.” = f (g s)
(f g) s would mean something different
f g s would be ambiguous
By convention, “¬” takes precedence over
“” and “” takes precedence over “”.
¬s f means (¬s) f , not ¬ (s f)
Transparency No. 1-17
The Foundations
The Implication Operator
The implication p q states that p implies q.
I.e., If p is true, then q is true;
but if p is not true, then q could be either
true or false.
E.g., let p = “You study hard.”
q = “You will get a good grade.”
p q = “If you study hard, then you will get
a good grade.” (else, it could go either way)
in p q , p is the antecedent and q is the
consequent of the implication.
Transparency No. 1-18
The Foundations
Implication Truth Table
p q is false only when
p q pq
p is true but q is not true. F F
T
p q does not say
F T T
that p causes q!
T F
F
p q does not require
T T T The
that p or q are ever true!
only
False
E.g. “(1=0) pigs can fly” is TRUE!
case!
Transparency No. 1-19
The Foundations
Examples of Implications
“If this lecture ends, then the sun will rise
tomorrow.” True or False?
“If Tuesday is a day of the week, then I am
a penguin.” True or False?
“If 1+1=6, then ChenShuaBen is president. ”
True or False?
“If the moon is made of green cheese, then
I am richer than Bill Gates.” True or False?
Transparency No. 1-20
The Foundations
English Phrases Meaning p q
“p implies q”
“if p, then q”
“if p, q”
“when p, q”
“whenever p, q”
“q if p”
“q when p”
“q whenever p”
“p only if q”
“p is sufficient for q”
“q is necessary for p”
“q follows from p”
“q is implied by p”
We will see some equivalent
logic expressions later.
Transparency No. 1-21
The Foundations
Converse, Inverse, Contrapositive
Some terminology, for an implication p q:
Its converse is:
q p.
Its inverse is:
¬p ¬q.
Its contrapositive:
¬q ¬ p.
Which of the above three has the same
meaning (logical equivalent; same truth
table) as p q ?
Ans: ¬q ¬ p.
Transparency No. 1-22
The Foundations
How do we know for sure?
Proving the equivalence of p q and its
contrapositive using truth tables:
p
F
F
T
T
q q
F T
T F
F T
T F
p
T
T
F
F
pq q p
T
T
T
T
F
F
T
T
Transparency No. 1-23
The Foundations
Boolean Operations Summary
We have seen 1 unary operator (out of
the 4 possible) and 5 binary operators
(out of the 16 possible). Their truth
tables are below.
p
F
F
T
T
q
F
T
F
T
p pq pq pq pq pq
T F
F
F
T
T
T F
T
T
T
F
F F
T
T
F
F
F T
T
F
T
T
Transparency No. 1-24
The Foundations
Some Alternative Notations
Name:
Propositional logic:
Boolean algebra:
C/C++/Java (wordwise):
C/C++/Java (bitwise):
not and or
p pq +
! && ||
~ & |
xor implies
!=
^
iff
==
Logic gates:
Transparency No. 1-25
The Foundations
Bits and Bit Operations
A bit is a binary (base 2) digit: 0 or 1.
Bits may be used to represent truth values.
By convention:
0 represents “false”; 1 represents “true”.
Boolean algebra is like ordinary algebra
except that variables stand for bits, +
means “or”, and multiplication means
“and”.
See chapter 10 for more details.
Transparency No. 1-26
The Foundations
Bit Strings
A Bit string of length n is an ordered series
or sequence of n0 bits.
By convention, bit strings are written left to
right: e.g. the first bit of “1001101010” is 1.
When a bit string represents a base-2
number, by convention the first bit is the
most significant bit. Ex. 11012=8+4+1=13.
Transparency No. 1-27
The Foundations
Bitwise Operations
Topic #2 – Bits
Boolean operations can be extended to
operate on bit strings as well as single bits.
E.g.:
01 1011 0110
11 0001 1101
11 1011
Bit-wise OR
01 0001
Bit-wise AND
10 1010
Bit-wise XOR
Transparency No. 1-28
The Foundations
End of §1.1
You have learned about:
Propositions: What
they are.
Propositional logic
operators’
Symbolic notations.
English equivalents.
Logical meaning.
Truth tables.
Atomic vs. compound
propositions.
Alternative notations.
Bits and bit-strings.
Next section: §1.2
Propositional
equivalences.
How to prove them.
Transparency No. 1-29
The Foundations
§1.2 Propositional Equivalence
Two syntactically (i.e., textually) different
compound propositions may be semantically
identical (i.e., have the same meaning). We call
them equivalent.
Learn:
Various equivalence rules or laws.
How to prove equivalences using symbolic
derivations.
Analogy:
x * (5 + y) and xy + 5x are always equal in algebra. But
how about
p /\ (q \/ r) and (p/\q) \/ (p /\ r) ?
Transparency No. 1-30
The Foundations
Tautology, contradiction and contingency
Some definitions: Let A be any proposition,
then
1. A is a tautology(contradiction) iff A is true
(false) no matter what the truth values of the
prop. variables inside A are given.
2. If A is neither a tautology nor a
contradiction, then A is called a contingency.
Contingencies
Tautologies
(valid)
Contradictions
(unsatisfiable)
The geography of propositions
Transparency No. 1-31
The Foundations
Examples:
p \/ ~p, p p : a tautology
p /\ ~p : a contradiction
p, p ~p, ~p p : a contingency
Transparency No. 1-32
The Foundations
Logical Equivalence
Topic #1.1 – Propositional Logic: Equivalences
proposition A is logically equivalent to
proposition B, written A B, IFF the
compound proposition AB is a tautology.
Note:1. is a logical symbol (connective)
whereas is a meta logical symbol.
2. The textbook uses instead of .
Propositions A and B are logically
equivalent to each other
iff
A and B contain the same truth values as
each other in all rows of their truth tables.
Transparency No. 1-33
The Foundations
Logical Equivalence
Theorem1: Logical equivalence relation is reflexive,
symmetric and transitive.
I.e., for all propositions A,B and C,
1. A A
2. A B implies B A and
3. A B and B C imply A C.
Theorem2[substitution theorem]: If A B and C[X] is
a proposition containing X as a subproposition, then
C[A] and C[B] are logically equivalent, where C[A] is
the result of C with X in C replaced by A.
ex: (p∨q) (q∨p), C[X] =def ~(p ∧ X)
=> ~(p∧ (p∨q) )~(p∧ (q∨p))
Transparency No. 1-34
The Foundations
Determine tautologies, contradictions and contingencies
Problems: Given a proposition A, how can you determine
whether it is a tautology, a contradiction or a contingency?
=>Exhausted evaluation! (by using truth table)
e.g., A = (p->q) <-> (~p \/q) a tautology ?
1. there are two primitive props: p, q.
2. So there are 4 possible assignments of truth values to p
and q.
p=0,q=0: p=0,q=1:
p=1,q=0:
p=1,q=1:
3. Under each assignment, we can evaluate the truth value of
A (in bottom up way) by the truth condition rule of
connecting connectives.
Transparency No. 1-35
The Foundations
Determine tautologies
(pq)<->~p\/q :1
p->q:1
~p:1
p:0
~p \/q:1
q:0
The evaluation tree for (p->q)<-> (~p\/q)
p
q
~p p->q
~p\/q
p->q <-> ~p\/q
0
0
1
1
1
0
1
1
1
T
1
0
0
1
1
0
1
1
1
0
1
0
1
1
1
The truth table for pq <-> ~p\/q
A tautology
since all are 1’s
Transparency No. 1-36
The Foundations
Determine other properties
1. logical equivalence: A B iff A<->B is a tautology.
So we can apply the procedure for determining
tautology to determine if A B.
Or A and B have the same truth values in all rows of their truth
table.
2. contradiction: A is a contradiction (恆假) iff ~A is a
tautology (恆真)
3. Satisfiability: A is satisfiable (可為真) iff ~A (可為假) is
not a tautology.
4. contingence: A is a contingence iff neither A nor ~A
is a tautology.
5. logical consequence: B is a logical consequence of
A [denoted A |= B] iff AB is a tautology.
Transparency No. 1-37
The Foundations
Topic #1.1 – Propositional Logic: Equivalences
Proving Equivalence via Truth Tables
Ex. Prove that pq (p q).
p
F
F
T
T
q
F
T
F
T
pq p q p q (p q)
F
T T
T
F
T
T F
F
T
T
F T
F
T
T
F F
F
T
Transparency No. 1-38
The Foundations
Example
Show that ~(p \/q) and ~p /\~q are logically
equivalent.
pf: The truth table for both propositions are given
below. Since the columns for ~(p\/q) and ~p /\ ~q
are equal, by definition, they are equivalent.
p
q
p\/q
~(p\/q)
~p
~q
~p /\ ~q
T
T
T
F
F
F
F
T
F
T
F
F
T
F
F
T
T
F
T
F
F
F
F
F
T
T
T
T
Transparency No. 1-39
The Foundations
Exercise
Show that pq ~p \/ q
pf: The truth table for both propositions are given
below:
p
q
~p
pq
~p \/ q
Since the columns for pq and ~p \/ q are equal, by
definition, they are equivalent.
Transparency No. 1-40
The Foundations
Exercise
Show that p\/(q/\r) and (p/\q) \/ (p/\r) are logically
equivalent.
p
q
r
q/\r
p\/(q/\r)
p/\q
p/\r
(p/\q)\/)p/\r)
• These columns can be skipped if you are familiar with the evalatiuon rules of
logical connectives.
Transparency No. 1-41
The Foundations
Equivalence Laws
Topic #1.1 – Propositional Logic: Equivalences
In algebra, we make use of equality
reasoning to replace equal by equal:
Ex:
Given the know equality: x + y = z,
we have x + (x + y) = x + z.
Thanks to substitution theorem, we can do
also equality reasoning for logical
expressions. Ex:
since p \/ p p,
q /\ ( p \/ p) q \/ p
Transparency No. 1-42
The Foundations
Topic #1.1 – Propositional Logic: Equivalences
Equivalence Laws - Examples
Identity:
pT p
pF p
Domination:
pT T
pF F
Idempotent:
pp p
pp p
Double negation:
p p
Commutative: pq qp pq qp
Associative:
(pq)r p(qr)
(pq)r p(qr)
Note. The textbook uses instead of .
Transparency No. 1-43
The Foundations
More Equivalence Laws
Distributive:
Topic #1.1 – Propositional Logic: Equivalences
p(qr) (pq)(pr)
p(qr) (pq)(pr)
De Morgan’s:
(pq) p q
(pq) p q
generalization:
~ (p /\ q /\ r …) ~p \/ ~q \/ ~r \/ …
Trivial tautology/contradiction:
p p T
p p F
Transparency No. 1-44
The Foundations
One Example:
Show that
~(p \/ (~p /\ q)) ~p /\ ~q
Proof:
1. By truth table (omitted)
2. ~(p \/ (~p /\ q) deM
~p /\ ~(~p /\ q) deM
~p /\ (~(~p) \/ ~q) DbNeg [+substitution]
~p /\ (p \/ ~q) Distr
(~p /\ p) \/ (~p /\ ~q) TrivalContradition
F \/ (~p /\ ~q) identity
(~p /\ ~q)
Transparency No. 1-45
The Foundations
Topic #1.1 – Propositional Logic: Equivalences
Defining Operators via Equivalences
Using equivalences, we can define operators
in terms of other operators.
Exclusive or: pq (pq)~(pq)
pq (pq)(q~p)
Implies:
pq p q
Biconditional: pq (pq) (qp)
pq ~(pq)
Boolean Algebra uses ~ as operations
Boolean Ring uses T as operations
~p p T ; (p \/ q) (pq p q)
Transparency No. 1-46
The Foundations
An Example Problem
Topic #1.1 – Propositional Logic: Equivalences
Check using a symbolic derivation whether
(p q) (p r) p q r.
(p q) (p r) [definition of ]
(p q) (p r) [Defn. of ]
(p q) ((p r) (p r))
[DeMorgan’s Law + DoubleNeg]
(p q) ((p r) (p r)) [ commutes]
(q p) ((p r) (p r))
Transparency No. 1-47
The Foundations
Example Continued...
Topic #1.1 – Propositional Logic: Equivalences
(q p) ((p r) (p r)) [ associative]
q (p ((p r) (p r))) [distrib. over ]
q (((p (p r)) (p (p r))) [assoc.]
q (((p p) r) (p (p r))) [trival taut.]
q ((T r) (p (p r))) [domination]
q (T (p (p r))) [identity]
q (p (p r)) cont.
Transparency No. 1-48
The Foundations
End of Long Example
Topic #1.1 – Propositional Logic: Equivalences
q (p (p r))
[DeMorgan’s]
q (p (p r))
[Assoc.]
q ((p p) r)
[Idempotent]
q (p r)
[Assoc.]
(q p) r
[Commut.]
p q r
Q.E.D. (quod erat demonstrandum)
(Which was to be shown.)
Transparency No. 1-49
The Foundations
Topic #1 – Propositional Logic
Review: Propositional Logic (§§1.1-1.2)
Atomic propositions: p, q, r, …
Boolean operators: (~)
Compound propositions: (p q) r
Equivalences: pq (p q)
Proving equivalences using:
Truth tables.
Symbolic derivations. p q r …
Transparency No. 1-50
The Foundations
Logical puzzles
Knight or knave:
Two kinds of inhabitants lived in an island
Knights : always tell the truth
Knaves : always lie.
Dialog of two people A and B lived in the
island:
A : “You are a knight”,
B: “ We are opposite types”
Question: What are the kinds of A and B ?
Transparency No. 1-51
The Foundations
Solution:
Formalization :
Let p = “ A is a knight” ; ~p “A is a knave”
Let q = “B is a knight” ; ~q “B is a knave”
Observed facts:
1. since A says q, we have
p q (1) /\ ~p ~q (2)
2. since B says R where
R is (p /\ ~q) \/ ( ~p /\ q) ) (5) , we have
q R (3) /\ ~q ~R (4).
The problem then reduces to : what is the model of P= (1)/\(2)/\(3)/\(4) ?
Analysis:
p true =(1)=> q true =(3)=> R true
=(5)=> R false (a contradiction!)
P false =(2)=>q false =(4)=> ~R => ~p /\ ~q. (consistent).
Conclusion: Both are knaves!!
(since P has only one model: [ p:false, q:false] ).
Transparency No. 1-52
The Foundations
Muddy Children puzzle ( reasoning about knowledge)
Two children Son and Daughter getting dirty mud
on their foreheads.
Father says to them: “At lest one of you has a muddy
forehead.” (1)
F2S: Do you know whether you have a muddy
forehead?
S : No,
Then, F2D: Do you know whether you have a muddy
forehead?
D: Yes.
Problem: Why did S and D answer No and Yes,
respectively?
Transparency No. 1-53
The Foundations
Analysis
Let d = “D has a muddy forehead”
s = “S has a muddy forehead”
Observed facts:
1. d \/ s. Hence know(S, d \/ s) and know(D, d \/ s)
2. Since both children can see each other’s forehead but
cannot see their own foreheads.
we have know(S, d), Hence S only knows
{d, d \/ s}, which cannot make him infer that s is true.
Hence S answered no when he was asked.
3. D’s inference when asked:
~d => Know(S, ~d) => Know(S, {~d, d \/ s }) => know(S, s)
=> S answered Yes.
Now since S did not answer Yes, ~d must be false (i.e., d
must be true), => D answered yes.
Transparency No. 1-54
The Foundations
1.3 Predicates (述詞) and quantifiers(量詞)
Problems of Propositional logic:
Cannot analyze the content of primitive
propositions.
cannot group similar propositions
cannot analyze quantifiers.
Ex: Consider the following situations:
1. Family = {f,m,c1,c2,c3 }
2. We are interested in who is whose
brother.
3. Suppose in Family, ci is cj’s brother if i
j for i,j =1..3.
Transparency No. 1-55
The Foundations
Inadequacy of propositional logic
Primitive propositions needed:
x_is_y’s_brother, x,y Family
So we need 25 propositions.
New approach: Parameterized
proposition(Predicate).
Use a (predicate) symbol B to symbolize the
statement:
B(x,y) x is y ‘s brother.
e.g.,
B(f,c1) : f is c1’s brother,
B(c2,c2) : c2 is c2’s brother,
...
Transparency No. 1-56
The Foundations
Benefits of Predicates
Advantage of using predicates:
==>
1. need only 6 (1 predicate and 5 names)
symbols.
2. can group related propositions together.
(B(x,y) and others, for instance,
q(x) x_isOld. )
3.The most important : allow representation of
quantified statement like: c1_has_a_brother (or,
there is an object x which is c1’s brother, $ x B(x, c1))
to be inferred from
c2_is_c1’s brother ( B(c2,c1) )
Transparency No. 1-57
The Foundations
Predicates
In the expression:
B(x,y)
B : predicate symbol (or proposition function)
x (y) : first (2nd) argument
B(x,y) : [atomic] proposition(or formula)
#arguments in B(X,Y): the arity of the predicate
symbol B.
Notes:
1. Each predicate symbol has a fixed arity.
2. B(x,y,c1) and B(x) are meaningless.
because used #arguments different from B’s arity.
Transparency No. 1-58
The Foundations
Predicates (cont’d)
3. The truth value of a proposition p(x1,...,xn)
depends on both p and real values of x1,...,xn.
Ex1: Let p(x) “x >3 “. then
P(4) “4 > 3” has truth value T,
P(2) “2 > 3” has truth value F.
Ex2: Let Q(x,y) “x = y +3” then
Q(1,2) = “1 = 2 + 3” is false.
Q(3,0) = “3 = 0 + 3” is true.
Mathematically, we can define (the meaning of) P as a
propositional function [P]
[P]: Un (n is P’s arity) {T,F}with the intention that
“P(x1,...,xn)” holds (is true) iff [P]([x1],...,[xn]) = T.
Transparency No. 1-59
The Foundations
Set representations of truth-functions
Ex:
[B]: Family2 -->{T,F} s.t. [B](x,y) = T iff x =[ci], y=[cj], i j.
P(x) “x >3 “ , So [P]: N --> {T,F } s.t. [P](x) = T iff x > 3.
Q(x,y) “x = y +3” , so
[Q] : N2 --> {T,F} with
[Q](x,y) = T iff x = y +3.
Note: [P] partition N into two sets, one with members
So, instead of represent
mapped to T and one mapped to F.
[P](x) = T. P as a truth function, we
equivalently represent P
{1,2,3}
{4,5,...}
as the set {x | [P](x) = T
} = {4,5,6,...}
[P](x) = F
Similarly, we can represent Q as {(x,y) | x = y + 3 }
N
Transparency No. 1-60
The Foundations
constant, function, variables and terms
In the statement:
“y > min(x, 3)” --- (s1)
x,y are called variables,
3 is a constant (symbol),
min is a function symbol with arity 2
“min(3,2)” behaves more like x, 3 than “x > y”.
So if let P(x,y) “x > y”, then
s1 can be represented as
P(y, min(x,3))
we call any expression that can be put on the
argument position of an atomic proposition a term
Obviously, constants and variables are terms;
moreover,if f is a function of arity n, and t1,...tn are n
terms, then so is f(t1,...,tn).
Transparency No. 1-61
The Foundations
Quantifiers and universe of discourse
Consider the sentence: p(x) =def “x > 0”.
1. as stated before, p(x) is true or false depending on
the value of x.
2. p(1), p(2),... : true;
p(0) , p(-1),...: false
Universe of Discourse (U,論域):
The set of objects (domain) from which all variables
are allowed to have values.
Ex: consider the sentence:
s2: ”all numbers are greater than 0”.
(for-all x “x > 0” ) or (" x p(x) )
U = N+={1,2,3,...} => s2 is true. U = Z={...,-1,0,1,...}=>
s2 is false.
Transparency No. 1-62
The Foundations
Universal and existential quantifications
A: any statement (or called formula)
e.g., A = p(x,y) /\ q(x,f(3)),...
x: any variable,
Then
1. ("x A) is a new formula called the universal
quantification of A,
2. ("x A) means:
“A(x) is true for all values of x in the universe of
discourse.”
3. ($x A) is a new formula called the existential
quantification of A,
4. ($x A) means:
“A(x) is true for some value of x in the universe of
discourse.”
Transparency No. 1-63
The Foundations
Truth conditions for quantifications
quantification
When ture ?
When false ?
("x A)
A is true for
every x
There is an x for
which A is false.
($x A)
There is an x for A is false for
which A is true. every x.
Logical equivalences:
1. ~("x A) ($x ~A)
2.~($x A) ("x ~A)
Transparency No. 1-64
The Foundations
The Universal Quantifier "
Topic #3 – Predicate Logic
Example:
Let the u.d. of x be {1,2,3,4}
Let P(x) be the predicate “x2 > 10.”
Then the universal quantification of P(x), "x P(x),
is the proposition:
All numbers x (in u.d.) satisfy the predicate x2 >
10
which is ture if
P(1), P(2),P(3), P(4) all hold, i.e., (P(1) /\ p(2) /\(3) /\ p(4) ).
But since P(2) = “22 > 10 “ is false, the universal
quantification is thus false.
Transparency No. 1-65
The Foundations
The Existential Quantifier $
Topic #3 – Predicate Logic
Example:
Let the u.d. of x be all natural numbers N = {0,1,2,3,4,…}
Let P(x) be the predicate “x2 > 10.”
Then the existential quantification of P(x), $x P(x), is the
proposition:
Some number x (in u.d.) satisfy the predicate x2 > 10
which is ture iff
one of P(0),P(1), P(2),P(3), P(4), … holds, i.e., (P(0) \/ p(1) \/ (2) \/ … ).
since P(4) = “42 > 10 “ is true, the existential quantification is thus
true.
Transparency No. 1-66
The Foundations
Translation of NL statements into logical ones
Translate the following sentences into logical expressions:
1. Everybody likes Wu
1' Wang is a kind teacher.
2. Every student dislikes some teacher.
3. John gives every student a book.
4. Nobody likes everybody.
5. There is somebody Wu don’t like.
6. There is somebody no one likes.
7. There is exactly one person everybody likes.
8 Wu likes more than one person
9. Everyone likes himself.
10. Nobody likes those who don't like themselves (沒人喜歡不自
愛的人 ).
Transparency No. 1-67
The Foundations
Solutions
1. Everybody likes Wu
1': Wang is a kind teacher.
"x like(x, Wu)
teacher(Wang) /\ kind(Wang)
2. Every student dislikes some teacher.
"x ( student(x) -> $y (teacher (y) /\ ~like(x, y))
3. John gives every student a book.
"s ( student(s) -> $b (book(b) /\ give(John, s, b))
4. Nobody likes everybody.
~$x"y like(x, y)
or "x $y ~like(x, y)
rules:
1. verb unary, binary predicate depending on its kind.:
ex: like -> binary, sleep, run ->unary, give ->ternary
2. proper noun constant
ex: Wu, John,…
3. common noun, adjective unary predicate
ex: teacher, student, kind -> unary predicate
4.不定代名詞 ( everybody/anybody/somebody : forall "
all/each/every/some : exists $
none : ~$ )
Transparency No. 1-68
The Foundations
5.There is somebody Wu don’t like.
6. There is somebody no one likes.
$y~ $ x like(x, y)
7.there is exactly one person everybody likes.
$y (
$y (
("x like(x, y) /\
("x like(x, y) /\
~$z (~z = y /\ "w like(w, z) ) )
"z ("w like(w, z) z = y ) )
or
8 John likes more than one person.
$xy ( ~(x = y) /\ like(john,x) /\ like(john, y).
9. Everyone likes himself.
"y like(y, y)
10.Nobody likes those who don't like themselves (沒人喜歡不自愛的人 ).
~$x $y ( ~like(y,y) /\ like(x,y) )
"x "y ( ~like(y,y) ~like(x,y) )
10' No boy likes any girl who don't like herself.
~$x (boy(x) /\ $y ( (girl(y) /\ ~like(y,y) ) /\ like(x,y) ))
"x (boy(x) -> "y ( (girl(y) /\ ~like(y,y)) ~like(x,y) )).
11. Everybody likes his father. 11' Everybody likes his parents.
"x (like(x, father(x)).
"x "y parent(y,x) > like(x, y).
Notes: father is a function symbol; parent is a binary predicate.
Transparency No. 1-69
The Foundations
Summary of the syntax of predicate logic
Suppose we are given the following sets of
symbols (Vocabulary) :
1. Object variables: x,y,z,…
2. Predicate symbols: p,q,r,…
3. function symbols : f, g, h,…
4. constant symbols: a,b,c,…
Notes:
1. (2,3,4) together is called a signature, which can be
designated by users according to their application while
(1) is usually predefined by the logic.
2. Constant symbols may be viewed as function symbols
of zero-arity.
Transparency No. 1-70
The Foundations
The syntax of predicate logic
A signature Sis a triple( F, P, ar) where F is a set of
function symbols and P is a set of predicate
symbols, and ar: P U F N is the arity fuction.
(1) If f F, then f is a function symbol of S of arity ar(f).
(2) If n = 0, then f is a constant.
(3) If p P, => p is a predicate symbol of arity ar(p).
(4) If n = 0 => p is an atom or proposition.
(5) Fun(S) = F is the set of function symbols
(6) Pred(S) = P is the set of predicate symbols
Ex: Arith =({0, 1, suc + *} , { >, =}, ar )
String=({e, *},{ < }, ar) ...
Transparency No. 1-71
The Foundations
Terms
Terms (object expressions) :
1. Every variable x or constant symbol b is a term
2. if f is a function symbol of arity k>0, and t1,…,tk are
known terms, then f(t1,…,tk) is a term.
Ex:
x: variable
---------------- 1
x: term ; mother: function symbol
--------------------------------------- 2
mother(x) : term;
father : unary function symbol
---------------------------------------------------------------------------2
father(mother(x)) :term
Transparency No. 1-72
The Foundations
Hierarchy of definitions:
primitive symbols terms atomic formula (general)
formula.
Atomic Formuls:
if p is a predicate symbol of arity k≥0 , and t1,…tk are
terms, then p(t1,…,tk) is an atomic formula.
note: zero-arity predicate symbols are propositional is
variables in propositional logic.
Formula:
1. Every atomic formula is a formula.
2. If A and B are formulas, then
(A/\B)2.1, (A\/B) 2.2, (A -> B) 2.3, (A B), A<->B, and ~A are
formulas.
3. if x is a variable and A is a formula, then
"X A3.1 and $X A3.2 are formula.
Transparency No. 1-73
The Foundations
Example
Show that "x (boy(x) -> like(x, father(x)) )) is a formula.
pf:
….
…
….
------------------ ------------------x:term; boy:predicate x:term; father(x):term; like : predicate
--------------------------- AF ----------------------------------------------------AF
boy(x):atomic
like(x, father(x)) :atomic
---------- ---------- 1
------------------------------------------1
boy(x) :formula
like(x, father(x)) :formula
---------------------------------------------------------------------------2.3
(boy(x) -> like(x, father(x))) :formula
---------------------------------------------------------3.1
"x (boy(x) -> like(x, father(x)) ) :formula
Transparency No. 1-74
The Foundations
S-structures and variable assignments
S : a signature.
A (first order) S-structure M is a triple:
(D, {[f]}f ∈ Fun(S), {[p]}p ∈ Pred(S) ) where
D is a nonempty set (of objects), called the domain of M
(,written DM).
[ f ]: Dar(f) -> D is a function on D of arity n. [f] is called the
denotation(or meaning) of f in M (, or written fM).
[p] Dar(p) {T,F} is a ar(p)-ary truth-function Dar(p)). [p] is
called the denotation (or meaning) of p in M (,written pM).
Variable M-assignment:
Any mapping a: Var -> DM from variables to the domain of a
S-structure M is called a variable M-assignment (or simply
an assignment).
Transparency No. 1-75
The Foundations
Denotations of terms in structures
syntactic objects
semantic objects (M, a)
----------------------------------------------------------------------function symbol(f)
function ([f] or fM)
constant(c)
domain object ([c] or cM)
predicate symbol(p)
truth funntion ([p] or pM)
variable (X)
domain object (a(X))
Terms
?
Formula
?
Transparency No. 1-76
The Foundations
Denotation of terms in a S structure
Given the pair (M,a), we can define a meaning
function (M,a) : T(S) -> DM inductively as
follows:
1. (M, a) (X) = a(X) for any variable X.
2. (M, a)(f(t1,..,tn)) = fM( (M, a)(t1),...,(M, a)(tn)),
where f is a function symbol of arity n, and t1,..,tn
are terms.
Note: (M,a)(c) = cM for constant symbol c (function
of arity zero)
Transparency No. 1-77
The Foundations
a: a variable assignment;
d: an object D;
X: a variable,
=> a[X/d] is a new variable assignment
agreeing with a on all variables but X, for
which it is assigned d. Formally,
a[X/d] is defined as follows: for all var Y :
a[X/d] (Y) =def if Y = X then d else a(Y)
Transparency No. 1-78
The Foundations
Truth condition of formulas
The relation M, a |= A (A is true (satisfied)
under interpretation M and assignment a) is
defined inductively as follows:
1. M, a |= p(t1,..,tn), iff
pM((M, a)(t1),..,(M, a)(tn)) = T.
2. M, a |= ~A iff not M, a |= A
3. M, a |= A \/ B iff M, a |= A or M, a |= B
4. M, a |= A /\ B iff M, a |= A and M, a |= B
5. M, a |= "X A iff M, a[x/d] |= A for all d D.
6. M, a |= $X A iff M, a[x/d] |= A for some d DM.
Transparency No. 1-79
The Foundations
Logical notions
A: a S-formula; T: a set of formulas
1. A is satisfiable iff there is S-structure M and an M-assignment
a s.t. M, a |= A.
2. A is valid iff for all S-structures M and for all M-assignment a,
M, a |= A.
3. A is valid in M iff for all M-assignments a, M, a |=A.
4. A is satisfiabe in M iff M, a |= A for some M-assignment a.
1' T is satisfiable iff there is a S-structure M and an Massignment a s.t. M, a |= A for all A in T.
2' T is valid in M iff for all M-assignments a, M, a |=A for all A in
T.
3' T is satisfiabe in M iff there is an assignment a s.t. M, a |= A
for all A in T.
Transparency No. 1-80
The Foundations
Semantical conclusion
A [or T ] is valid iff for all S-structures M and for all Massignment a, M, a |= A [for all A ∈ T ].
If A is valid in M,(denoted M |= A) we say M is a model of A.
T: a (set of) formulas; A: a formula
T |= A (,A is a logical consequence of T) iff
Every model of T is a model of A.
A and B are logically equivalent (denoted A B) iff A<-> B
is valid. (i.e., for any structure assignment pair (M, a), M, a
|= A iff M, a |= B.)
Transparency No. 1-81
The Foundations
syntactic objects and their meaning
syntactic object
examples
constant
a,b,c
semantical meaning
domain object
[a]
function symbol
f,g,h
domain function
[f] : Uarity U
predicate symbol
p,q, r,…
domain relations
(or truth function)
[p] : Uarity {t,f }
variable
x,y,z,…
? (determined by
assignment)
term
f(t1,…,tn)
domain object
[f] ([t1],…[tn])
atomic formula
(general) formula
f(t1,…,tn)
A,B,C
proposition (trut value)
[p] ([t1],…[tn])
truth value [A] dertermined
by components.
Transparency No. 1-82
The Foundations
Some Terminology
Occurrences of variables
Free/Bound Variables
Transparency No. 1-83
The Foundations
Occurrences of variables in a formula
Let A = p(f(x),c) \/ q(x,y)
A contains 2 variables x, y, where x occurs
twice and y occurs once.
Transparency No. 1-84
The Foundations
Free and Bound Variables
Topic #3 – Predicate Logic
An expression like p(x) , where p is a
predicate symbol, is said to have a free
variable x (meaning, x is undefined).
A quantifier (either " or $) operates on an
expression having one or more free
variables, and binds one or more of those
variables, to produce an expression having
one or more bound variables.
ex: "x p(x,y).
Note: x is like a declared local variable wile y is
like an undeclared local variable in
programming language..
Transparency No. 1-85
The Foundations
Example of Binding
Topic #3 – Predicate Logic
p(x,y) has 2 free variables, x and y.
"x p(x,y) has 1 free variable, and one bound
variable. [Which is which?]
An formula with zero free variables is a sentence
(or proposition).
An formula with one or more free variables is still
only a predicate: "x P(x,y)
Note: we use expression and formula
interchangeably as logical expressions are
usually called formulas.
Transparency No. 1-86
The Foundations
Formalization of free variables
A: a formula (or expression)
fv(A) = the set of all free variables in A is defined as
follows:
If A is atomic => fv(A) is the set of all variables in
A
fv(~A) = fv(A)
fv(A/\B)=fv(A\/B)=fv(A->B)=fv(A<->B)= fv(A) U
fv(B).
fv("x A) = fv($xA) = fv(A) \ {x}.
What is fv(A) where A is an atomic formula?
can be defined by recursion also:
1. var(t) = {t} if t is var
2. var(t) = var(t1) U var(t2)…U var(tn) if t =
f(t1,t2,…tn) or p(t1,…tn).
Finally let fv(A) = var(A) if A is an atomic
formula.
Transparency No. 1-87
The Foundations
Formalization of bound variables
bd(A): the set of bound variables in A is defined as
follows;
1. If A is atomic => bd(A) = {}
2. bd(~A) = bd(A)
3. bd(A/\B) = d(A\/B) = bd(AB)
=bd(A<->B) = bd(A) U bd(B).
4. bd( ∀x A) =
bd(A) if x ∉ fv(A).
bd(A) U {x} if x ∈ fv(A).
Example A = ($ x p(x,y)) \/ q(x)
=> fv(A) = {x,y}; bd(A) = {x}
x occurs twice in A, one occurs free and the other
occurs bound.
Def: A is a sentence iff fv(A) = {}
Note: A is a proposition if A is a sentence
Transparency No. 1-88
The Foundations
Conventions
Topic #3 – Predicate Logic
Sometimes the universe of discourse is
restricted within the quantification, e.g.,
"x>0 P(x) is shorthand for
“For all x that are greater than zero, P(x).”
="x (x>0 P(x))
$x>0 P(x) is shorthand for
“There is an x greater than zero such that P(x).”
=$x (x>0 P(x))
Transparency No. 1-89
The Foundations
More to Know About Binding
Topic #3 – Predicate Logic
"x $x P(x)
x is not a free variable in
$x P(x), therefore the "x binding isn’t used.
("x P(x)) Q(x)
The variable x in Q(x) is outside of the scope
of the "x quantifier, and is therefore free. Not
a proposition!
("x P(x)) ($x Q(x))
This is legal, because there are 2 different x’s!
Transparency No. 1-90
The Foundations
Quantifier Equivalence Laws
Topic #3 – Predicate Logic
Definitions of quantifiers: If u.d.={ a,b,c,…}
"x P(x) P(a) P(b) P(c) …
$x P(x) P(a) P(b) P(c) …
From those, we can prove the laws:
"x P(x) $x P(x)
$x P(x) "x P(x)
Which propositional equivalence laws can
be used to prove this?
DeMorgan’s Law
Transparency No. 1-91
The Foundations
More Equivalence Laws
Topic #3 – Predicate Logic
"x "y P(x,y) "y "x P(x,y)
$x $y P(x,y) $y $x P(x,y)
"x (P(x) Q(x)) ("x P(x)) ("x Q(x))
$x (P(x) Q(x)) ($x P(x)) ($x Q(x))
Transparency No. 1-92
The Foundations
Some Number Theory Examples
Topic #3 – Predicate Logic
Let u.d. = the natural numbers 0, 1, 2, …
“A number x is even, E(x), if and only if it is
equal to 2 times some other number.”
"x (E(x) ($y x = 2 * y ))
“A number is prime, P(x), iff it’s greater
than 1 and it isn’t the product of two nonunity numbers.”
"x (P(x) (x>1 $yz x=yz y1 z1))
Transparency No. 1-93
The Foundations
Goldbach’s Conjecture (unproven)
“Every even number greater than 2
is the sum of two primes.”
"x [x>2 E(x)] →
$y $z ( P(y) P(z) y+z = x ).
Transparency No. 1-94
The Foundations
Calculus Example
Topic #3 – Predicate Logic
One way of precisely defining the
calculus concept of a limit, using
quantifiers:
(lim f ( x) L)
x a
" 0 : $ 0 : "x :
(| x a | ) (| f ( x) L | )
Transparency No. 1-95
The Foundations
End of §1.3-1.4, Predicate Logic
Topic #3 – Predicate Logic
From these sections you should have
learned:
Predicate logic notation & conventions
Conversions: predicate logic clear English
Meaning of quantifiers, equivalences
Simple reasoning with quantifiers
Upcoming topics:
Introduction to proof-writing.
Set theory –
a language for talking about collections of objects.
Transparency No. 1-96
The Foundations
1.5 Rules of inference
The following 3 sections are about proofs.
Argument (論述):
Valid arguments
Argument form (pattern)
Rules of inference
For propositional reasoning
For quantifier reasoning
Transparency No. 1-97
The Foundations
Arguments
An argument is a sequence of statements made
to convince people of the truth of the final
conclusion.
Definition 1.1: An argument in logic is a sequence
of propositions:
A1, A2,…,An (n > 0)
The final one An is called the conclusion of the
argument,
Some of {A1,…,An} are called the premises of the
statements.
An argument is basic if all propositions but the final
one are premises.
Note: Our definition of argument is more general than
that given in the textbook, which corresponds to our
basic argument.
Transparency No. 1-98
The Foundations
Example of an argument
1. Have a passwd can log onto the network
(premise)
2. Can log onto the network can change grade (premise)
3. Have a passwd (premise)
Therefore :
4. can log onto the network (lemma)
5. can change the grade
(conclusion)
Notes: 1. 1..4 is a basic argument;
2. 1..5 is a non-basic argument.
Definition 1.2: An argument is valid if the truth of all its
premises implies the conclusion is true.
Note: Basic argument A1, A2,…,An is valid iff A1, A2,…,An-1
|= An or (A1/\ A2/\…An-1) An is a tautology.
Ex: the above argument (1..4 or 1..5) if valid since the
conclusion is true whenever all premises are true.
Transparency No. 1-99
The Foundations
Valid arguments and truth of conclusions
Note: An argument is valid does not mean that its
conclusion must be valid since it is possible that some of
the premises are false.
Ex: The following argument is valid
1. have access to the grading system can Change Grade
2. have access to the grading system
Therefore
3. can change the grade.
But (in the actual condition) the conclusion (3) is false since
premise (2) is false.
Note: A valid argument can guarantee the truth of its
conclusion only when all its premises are true.
Transparency No. 1-100
The Foundations
Argument forms
In the basic argument :
1. have access to the grading system can Change Grade
2. have access to the grading system
Therefore
3. can change the grade.
Let p represent “have access to the grading system “ and
q represent “can Change Grade”
Then the basic argument has the form (or pattern):
1.
pq
2.
p
3.
q
To save space, we may write the above form as :
pq, p // q
Transparency No. 1-101
The Foundations
Argument form
Definition 1.3 :
An argument form in logic is a basic argument of
which some propositions contain propositional
variables.
If A is an argument form and A’ is the result of
replacing all occurrences of each variable by a same
proposition, then A’ is said to be an instance of the
argument form A .
Ex: The argument form : p q, p // q has
instances:
raining wet, raining // wet,
studyHard GoodGrade, studyHard // goodGrade
pq , p // q
p \/ q ~r, p \/ q // ~r, but not
raining wet, raining // cloudy (why?)
Transparency No. 1-102
The Foundations
Argument forms and arguments
Def: An argument form A1,A2,…,An-1 // An in logic is valid
if (A1/\A2…/\An A) is a tautology.
Theorem : If an argument form A = (A1, .., //An) is valid
then all of its instances are valid.
Pf: This is a simple result of the substitution theorem of
propositional logic.
Let A’ = (A’1, .., A’n) be any instance of A. Then
A is valid iff B= (A1/\ A2/\…An-1) An is a tautology
=> B’ = (A’1/\ A’2/\…A’n-1) A’n is a tautology (substitution theorem)
=> argument A’ is valid.
Transparency No. 1-103
The Foundations
Analogy: When we say the equality x + x = 2 * x is valid, it
implies :
#Students + #students = 2 * #Students ; #sons + #sons = 2
#sons
( #students / #classe) + ( #students / #classe) = 2 * + ( #students /
#classe)
( x – z = 5) + (x – z + 5) = 2 * (x – z + 5), …
Similarly, if pq, p // q is valid then so are
raining wet, raining // wet,
studyHard GoodGrade, styudyHard // goodGrade
p \/ q ~r, p \/ q // ~r
Transparency No. 1-104
The Foundations
Rules of inferences
How to show the validity of an argument
form:
Solution 1: Truth table
If (A1, .., An) is an argument form with variables
p1,…,pm, then establish a truth table with 2m
rows for the target formula (A1/\A2…/\An-1) An
and then check if it is a tautology.
Problem: 2m is too large a number of rows to
check validity even for a small m (e.g., 20).
Solution 2: deduction:
Establish the validity of a (complicated)
argument forms from simpler known valid ones.
Transparency No. 1-105
The Foundations
Application of rules of inference
A rule of inference is an argument form
that is chosen to build the validity of other
argument forms.
A rule of inference is valid if it is a valid
argument form.
An invalid rule of inference is called a fallacy.
Ex:
Modus ponens (MP): pq, p // q
Conjunction
: p, q
// p /\ q
Abduction:
pq, q // p
(fallacy)
Transparency No. 1-106
The Foundations
Application of rules of inferences
Known assumptions (premises):
snow go skiing
snow
Then
1. Snow
2. Snow go skiing
3. Skiing
Is a valid argument.
1, 2 are premises
3 is the result of applying rule MP to 1 and 2.
Transparency No. 1-107
The Foundations
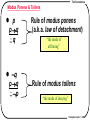
Modus Ponens & Tollens
p
pq
q
q
pq
p
Rule of modus ponens
(a.k.a. law of detachment)
“the mode of
affirming”
Rule of modus tollens
“the mode of denying”
Transparency No. 1-108
The Foundations
Some Inference Rules
p
pq
Rule of Addition
pq
p
Rule of Simplification
Rule of Conjunction
p
q
pq
Transparency No. 1-109
The Foundations
Syllogism Inference Rules
pq
qr
pr
hypothetical
syllogism
p q
p
q
disjunctive
syllogism
p \/ q, ~p \/ r // q \/ r
Resolution
Transparency No. 1-110
The Foundations
Build arguments using rules of inference
Suppose we have the following
assumptions (premises):
“It is not sunny and it is cold.”
“We will swim only if it is sunny.”
“If we do not swim, then we will dance.”
“If we dance, then we will be home early.”
Given these premises, try to give a valid
argument with the conclusin “We will be
home early” using inference rules.
Transparency No. 1-111
The Foundations
Example cont.
Abbreviations:
sunny = “It is sunny”; cold = “It is cold”;
swim = “We will swim”; dance = “We will dance”;
early = “We will be home early”.
Then, the premises can be written as:
(1) sunny cold
(2) swim sunny
(3) swim dance
(4) dance early
Transparency No. 1-112
The Foundations
Valid argument Example cont.
Step
1. sunny cold
2. sunny
3. swimsunny
4. swim
5. swimdance
6. dance
7. danceearly
8. early
Proved by
Premise #1.
Simplification of 1.
Premise #2.
Modus tollens on 2,3.
Premise #3.
Modus ponens on 4,5.
Premise #4.
Modus ponens on 6,7.
Transparency No. 1-113
The Foundations
Fallacies
A fallacy is an inference rule which is not
valid.
(I.e., It is possible that all premises are true
but the conclusion is false).
Ex:
fallacy of affirming the premise:
pq, q // p
// q true, pq true but p false is possible
Fallacy of denying the conclusion:
pq, ~p // ~q ;
Transparency No. 1-114
The Foundations
Inference Rules for Quantifiers
"x P(x) universal instantiation (UI)
P(t) (substitute any term t for x in P(-))
Ex: from "x x2 > 0 infer (y+2)2 > 0.
P(t)
existential generalization (EG)
$x P(x) (substitute a new var x for term t in P(-) )
ex: from (y + 2 )2 > (y+2)
infer
$x x2 > (y+2) or
$x x2 > x.
Note: Term t is either a constant c or a variable x or
function expression f(t1,…,tn)
Transparency No. 1-115
The Foundations
More Inference Rules for Quantifiers
universal generalization(UG)
P(g)
(where g is a constant referring to any
general (or universal) element of u.d. I.e.,
"x P(x)
g cannot be restricted to any property
except being an element of u.d.)
Existential instantiation (EI)
$x P(x)
P(c)
(substitute a new (Skolem)
constant c )
Note: c is an object restricted to property P
Transparency No. 1-116
The Foundations
Example
D(x) = “x has taken Discrete math course”
C(X) = “ x has taken a cs course”
Premises:
D(Chen), " x (D(x) C(x))
Argument
D(Chen)
" x (D(x) C(x))
D(Chen) C(Chen)
C(Chen)
premise
premise
UI
MP
Transparency No. 1-117
The Foundations
Example
Premises:
1. A student in this class has not read the
book,
2. Everyone in this class passed the exam
Expected conclusion:
Someone passing the exam has not read the
book.
Abbreviations:
C(x) : x is in this class
R(x) : x has read the book
P(x) : x has passed the exam.
Transparency No. 1-118
The Foundations
The arguments
1.
2.
3.
4.
5.
6.
7.
8.
9.
$x (C(x) /\ ~R(x) )
C(a) /\ ~R(a)
C(a)
"x (C(x) P(x) )
C(a) P(a)
P(a)
~R(a)
P(a) /\ ~R(a)
$x (P(X) /\ ~R(x)).
premise 1.
EI from 1
Simplification from 2
premise 2
UI 4
MP from 3,5
Simplification from 2
Conjunction 6,7
EG from 8
Transparency No. 1-119
The Foundations
Topic #3 – Predicate Logic
Example (skipped)
Definitions:
c :≡ Confucius ;
H(x) :≡ “x is human”;
M(x) :≡ “x is mortal”.
Premises:
H(c)
"x H(x)M(x)
Conclusion:
M(c)
Confucius is human.
All humans are mortal.
Confucius is mortal.
Transparency No. 1-120
The Foundations
The argument (skipped)
Topic #3 – Predicate Logic
Some valid conclusions you can draw:
H(c)
H(c)M(c)
premise
[Instantiate universal.] If Confucius is human
then he is mortal.
H(c) M(c)
Socrates is inhuman or mortal.
H(c) (H(c) M(c))
Confucius is human, and also either inhuman or mortal.
(H(c) H(c)) (H(c) M(c))
[Apply distributive law.]
F (H(c) M(c))
[Trivial contradiction.]
H(c) M(c)
[Use identity law.]
M(c)
Confucius is mortal.
Transparency No. 1-121
The Foundations
Example (universal genealization (UG )
The square of all odd numbers are odd.
"x Odd(x) Odd(x2)
pf: Let g be any number. // note: cannot assume additional
property for g except for its being an integer; g is a universal
constants.
[ Assume g is odd, then,
g = 2k + 1 for some k,
g2 = 4kk + 4k + 1 = 2(2kk + 2k) + 1,
g2 is odd. ] // [ … ] is a subproof for
=> Odd(g) Odd(g2).
=> "x Odd(x) Odd(x2).
Transparency No. 1-122
The Foundations
Example2
"x$y x < y. // no largest number
pf: Let a be any number.
=>a < a + 1 ( number property; true of all numbers)
(but not a2 < a + 10 ; not a universal number prop )
=> $y a < y (EG)
=> "x$y x < y (UG)
$x"y x y //least number
pf: Let a be any natural number.
=> 0 a ( property of natural numbers)
=> "y 0 y (UG)
=> $x"y x y (EG)
Transparency No. 1-123
The Foundations
a fallacy
Find an argument for $x P(x) |- "x P(x)
What’s wrong with the proof: ?
1. $x P(x)
2. P(c)
3. "x P(x)
--- premise
--- EI, where c is a restricted object.
--- UG (x) why?
Ans: 23 is wrong! c is not a general element! It
requires to satisfy property P and thus is not a
general element.
Transparency No. 1-124
The Foundations
Proofs and proof methods
Nature and importance of proofs
Applications of proofs
Proof terminology
Inference rules
Some inference rules
Soundness of inference rules
Formal proofs
Formal proof examples
Inference rules for quantifiers
common fallacies
proof methods
Transparency No. 1-125
The Foundations
Proof Terminology
Theorem [定理]
A statement that can be proven to be true.
Axioms[公設], postulates, hypotheses,
premises
Assumptions (often unproven) defining the
structures about which we are reasoning.
Rules of inference [推論法則]
Patterns of logically valid deductions from
hypotheses to conclusions.
Transparency No. 1-126
The Foundations
More Proof Terminology
Lemma[輔助定理] - A minor theorem used
as a stepping-stone to proving a major
theorem.
Corollary - A minor theorem proved as an
easy consequence of a major theorem.
Conjecture - A statement whose truth value
has not been proven. (A conjecture may
be widely believed to be true, regardless.)
Theory – The set of all theorems that can
be proven from a given set of axioms.
Transparency No. 1-127
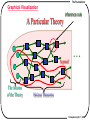
The Foundations
Graphical Visualization
inference rule
A Particular Theory
A proof
The Axioms
of the Theory
…
Various Theorems
Transparency No. 1-128
The Foundations
Formal Proofs
A formal proof of a conclusion C, given premises
p1, p2,…,pn is a sequence of statements :
A1,…,An=C,
each of which either is a premise or is the result
of applying some inference rule to premises or to
previously-proven statements.
I.e., for each k = 1 .. n, either
1. Ak is some premise Pj, or
2. there is an instance (D1,…,Dm, E) of a rule with
{D1,…,Dm} a subset of {A1,…,Ak-1} and Ak = E.
Transparency No. 1-129
The Foundations
More about proofs
Notes:
1. We use B |-Th A (or B1,…,Bm |-Th A)
to mean the existence of a proof of A with
B1,…,Bm as premises. (Th can be omitted if there
is no worry of confusion)
2. If {} |-Th A (or simply |-Th A) , we say A is a
theorem and each Ai (i <n) is called a lemma.
3. If B can be inferred from A directly, it is called a
corollary of theorem A; both lemmas and
corollaries are theorems.
Transparency No. 1-130
The Foundations
Soundness of a proof system
Soundness theorem: If
1. there is a proof of C from a set of premises P= {P1,… Pn }
(I.e., P1,…Pn |- C ), and
2. all inference rules used are sound,
then the proof is valid, i.e.,
conclusion C must be a consequence of {P1,… Pn}.
(i.e., P1,P2,…Pn |= C )
This theorem holds not only for propositional logic and
predicate logic but also for all logical systems.
Transparency No. 1-131
The Foundations
Corollary : If |-Th C, then |= C. I.e., Every theorem
is valid).
pf: |-Th C means {} |-Th C.
Hence {} |= C.
But all interpretations are model of {},
C thus is valid.
Transparency No. 1-132
The Foundations
Example
Topic #3 – Predicate Logic
Definitions:
s :≡ Socrates (ancient Greek philosopher);
H(x) :≡ “x is human”;
M(x) :≡ “x is mortal”.
Premises:
H(s)
Socrates is human.
"x H(x)M(x)
All humans are mortal.
Conclusion:
M(s)
Socrates is mortal.
Transparency No. 1-133
The Foundations
The proof
Topic #3 – Predicate Logic
Some valid conclusions you can draw:
H(s)M(s)
[Instantiate universal.] If Socrates is human
then he is mortal.
H(s) M(s)
Socrates is inhuman or mortal.
H(s) (H(s) M(s))
Socrates is human, and also either inhuman or mortal.
(H(s) H(s)) (H(s) M(s))
[Apply distributive law.]
F (H(s) M(s))
[Trivial contradiction.]
H(s) M(s)
[Use identity law.]
M(s)
Socrates is mortal.
Transparency No. 1-134
The Foundations
Techniques for proving implication theorems : pq
Different ways of proving a theorem: p implies q.
Vacuous proof: Prove that ~p. used rule : [ ~p //p->q ]
Trivial proof: Prove that q.
[q // p->q ]
Direct proof: Prove that if p then q. [p |- q implies |- p->q]
suppose p,
...,
conclude q
--------------------- (I)
hence pq
Indirect proof: (proof by contraposition)
Prove that "~q implies ~P" [~q->~p // p->q]
Transparency No. 1-135
The Foundations
Proof by contradiction and proof by cases
Proof by contradiction:
To prove P, it suffices to show that
~P -> F (false)
rules used: [~p ->F // p]
Proof by cases:
To prove that "p \/ q implies r " it suffices to show that
p->r and q -> r.
rules used: [p->r, q->r // (p\/ q) ->r.]
Transparency No. 1-136
The Foundations
Direct Proof Example
Definition: An integer n is called odd iff n=2k+1 for
some integer k; n is even iff n=2k for some k.
Axiom: Every integer is either odd or even.
Theorem: (For all numbers n) If n is an odd integer,
then n2 is an odd integer.
Proof: Let n be any integer.
[Assume n is odd, then
n = 2k+1 for some integer k. Thus,
n2 = (2k+1)2 = 4k2 + 4k + 1 = 2(2k2 + 2k) + 1.
Therefore n2 is of the form 2j + 1 (with j the integer
2k2 + 2k), thus
n2 is odd. ]
Transparency No. 1-137
The Foundations
Another example of direct proof
Show that |- (p(q r)) ((pq) (pr)).
Pf:
1. [Assume p (q r)
2. [assume pq
3.
[assume p
4.
q
MP+2,3
5.
q r
MP+1,3
6.
r]
MP+4,5
7.
pr ]
3~6 is a proof of pr
8. (pq ) (pr) ] 2~7 is its proof
9. (p(q r)) ((pq) (pr)). 1~8 is its proof.
Transparency No. 1-138
The Foundations
Indirect Proof Example
Theorem: (For all integers n)
If 3n+2 is odd, then n is odd.
Proof: Suppose that the conclusion is false, i.e.,
that n is even.
Then n=2k for some integer k.
Then 3n+2 = 3(2k)+2 = 6k+2 = 2(3k+1).
Thus 3n+2 is even, because it equals 2j for
integer j = 3k+1.
So 3n+2 is not odd.
We have shown that ¬(n is odd)→¬(3n+2 is odd),
thus its contra-positive (3n+2 is odd) → (n is odd)
is also true. □
Transparency No. 1-139
The Foundations
Vacuous Proof Example
Theorem: (For all n) If n is both odd and even,
then n2 = n + n.
Proof: The statement “n is both odd and even” is
necessarily false, since no number can be both
odd and even.
So, the theorem is vacuously true. □
lemma : n could not be both even and odd.
pf: Suppose n is both odd and even, then n = 2k = 2m
+ 1 for some integer m and k. Then 2(k-m) = 1.
Then k != m and hence 2 | 1. But this is impossible.
Transparency No. 1-140
The Foundations
Trivial Proof Example
Theorem: (For integers n) If n is the sum of two
prime numbers, then either n is odd or n is even.
Proof: Any integer n is either odd or even.
So the conclusion of the implication is true
regardless of the truth of the antecedent.
Thus the implication is true trivially. □
Transparency No. 1-141
The Foundations
Proving existence theorem
Methods for proving $x p(x):
Constructive proof: find an object (or term)
a, s.t. P(a).
rules used : p(a) // $x p(x)
;EG
Nonconstructive proof: a proof of $x P(x)
w/o knowing what object satisfies p.
Ex: proof by contradiction:
Show that ~$x p(x) F. or
("x ~p(X)) F.
Transparency No. 1-142
The Foundations
Example of existence proofs
Ex 20: [constructive proof] Show that there are n consecutive
composite integers for every integer n >0. (I.e. for all n $x
(x+1,x+2,...x+n) are all composites.
Sol: Let x = (n+1)! +1.
=> x+i = (n+1)! + (i+1) = (i+1)( (n+1)!/(i+1) +1) is composite for
i = 1,..,n. QED.
Ex 21: [nonconstructive proof] For all n >0 $ prime number > n.
Sol: by contradiction. Assume $n s.t. all prime number < n.
Let m = n! +1. ==> gcd(k, m) = 1 for all k ≤ n.
=> all primes cannot divide m
=> m is a prime > n
=> a contradiction. QED.
Note: We cannot know a prime > n from the proof.
Transparency No. 1-143
The Foundations
Example of proof by cases...
[No largest prime: ] Given n>0, prove there is a
prime p>n.
pf: Consider x = n!+1. Since x>1, we know
(x is prime)(x is composite).
Case 1: x is prime. Obviously x>n, so let p=x and
we’re done.
Case 2: x has a prime factor p. But if pn, then
x = (n!/p) x p + 1 => x 1 (mod p).
Then p does not divide x, a contradiction.
So p>n, and we’re done.
Transparency No. 1-144
The Foundations
Limits on Proofs
Some very simple statements of number theory
haven’t been proved or disproved!
E.g. Goldbach’s conjecture: Every integer n≥2 is
exactly the average of some two primes.
"n≥2 $ primes p,q: n=(p+q)/2.
For every formal proof system, there are true (or
false )statements of number theory which can
never be proved (or disproved) (Gödel
incompleteness theorem).
Transparency No. 1-145