Download j=1/2

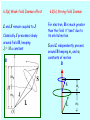
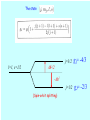
PHYS 30101 Quantum Mechanics
Lecture 20
Dr Jon Billowes
Nuclear Physics Group (Schuster Building, room 4.10)
[email protected]
These slides at: http://nuclear.ph.man.ac.uk/~jb/phys30101
6. The hydrogen atom revisited
- Reminder of eigenfunctions, eigenvalues and quantum
numbers n, l, ml of hydrogen atom.
6.1 Spin-orbit coupling and the fine structure.
6.2 Zeeman effect for single electron atoms in
(a) a weak magnetic field
(b) a strong magnetic field
6.3 Spin in magnetic field: QM and classical descriptions
RECAP: 6. 1 Spin-orbit coupling and “fine structure”
Classically an electron orbiting a nucleus of charge Ze “sees” the
nucleus in orbit around it (a current loop) which produces a field
at the electron of
Putting I= Ze/T where T is period of orbit (obtained from the
classical angular momentum expression L=meωr2 ) we get:
Electron magnetic moment is in direction of its intrinsic spin:
Thus interaction energy and corresponding Hamiltonian can be written
(relativistic effect of “Thomas precession”)
The shift in energy of a state
is the eigenvalue of the
spin-orbit Hamiltonian:
j=3/2 (4 states)
l=1, s=1/2
ml=+1, 0, -1
ms=+1/2, -1/2
(6 states)
Aħ2/2
-Aħ2
j=1/2 (2 states)
The energy centroid is unchanged: 4 X A/2 = 2 X A
6.2(a) Weak-field Zeeman effect
L and S remain coupled to J.
Classically J precesses slowly
around field B, keeping
Jz= M a constant
6.2(b) Strong-field Zeeman
For electron, B is much greater
than the field it ”sees” due to
its orbital motion.
S and L independently precess
around B keeping ms and ml
constants of motion
B
B
S
L
S
ms
L
ml
Landé g-factor
The state
l=1, s=1/2
j=3/2
gJ= -4/3
j=1/2
gJ= -2/3
Aħ2/2
-Aħ2
(Spin-orbit splitting)
Zeeman structure
Strong field
for l = 1, s = 1/2 orbital
Weak field
(-1,+1/2)
(+1,-1/2)