* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Precalculus Notes
Georg Cantor's first set theory article wikipedia , lookup
Vincent's theorem wikipedia , lookup
List of important publications in mathematics wikipedia , lookup
Wiles's proof of Fermat's Last Theorem wikipedia , lookup
Fermat's Last Theorem wikipedia , lookup
Central limit theorem wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Elementary mathematics wikipedia , lookup
Brouwer fixed-point theorem wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Non-standard calculus wikipedia , lookup
Four color theorem wikipedia , lookup
Weber problem wikipedia , lookup
History of trigonometry wikipedia , lookup
Precalculus
AF
T
© M. Sunil R. Koswatta 2014
DR
We want students to learn to reason mathematically and communicate their reasoning coherently. To reason mathematically means providing a logical argument for
any claim that you make, based only on prior knowledge of mathematics. In mathematical parlance, this process of providing a logical argument to justify a claim
is known as the “proof of the claim”. At any given point in the course, the prior
knowledge consists of the prerequisite mathematics and the mathematics students
have learned up to that point. The prerequisite mathematics include mathematics
of K-12 and the content of a college algebra course. In the process of learning, we
hope that students will acquire skills that are required in calculus and beyond.
I would like to thank Larry Francis and Bob Campbell for editing this document.
1
Contents
Contents
2
I Algebra
7
1 Equations and Inequalities
9
1.1
Quadratic Equations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
1.2
Rational Equations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
1.3
Radical Equations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
1.4
Equations That can be Written as Quadratic Equations . . . . . . . . . . . 19
1.5
Absolute-Value Inequalities
1.6
Quadratic Formula . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
1.7
Polynomial and Rational Inequalities . . . . . . . . . . . . . . . . . . . . . 28
. . . . . . . . . . . . . . . . . . . . . . . . . . 20
2 Graphs of Polynomial and Rational Functions
33
2.1
Graphs of Quadratic Functions . . . . . . . . . . . . . . . . . . . . . . . . 33
2.2
Graphs of Polynomial Functions . . . . . . . . . . . . . . . . . . . . . . . . 40
2.3
Graphs of Rational Functions . . . . . . . . . . . . . . . . . . . . . . . . . 46
3 Sequences, Series, Mathematical Induction
67
3.1
Sequences and Series . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
3.2
Mathematical Induction . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
4 Partial Fraction Decomposition
89
4.1
Solving Systems of Linear Equations (Review) . . . . . . . . . . . . . . . . 89
4.2
Partial Fraction Decomposition: Linear Factors . . . . . . . . . . . . . . . 94
4.3
Partial Fraction Decomposition: Irreducible Quadratic Factors . . . . . . . 100
2
CONTENTS
3
II Trigonometry
103
5 Trigonometry of Angles
5.1 Angles . . . . . . . . . . . . . . . . . . . . . . . .
5.2 Degree Measure of an Angle . . . . . . . . . . . .
5.3 Radian Measure of an Angle . . . . . . . . . . . .
5.4 Relationship between the Degree Measure and the
5.5 Trigonometric Numbers of Angles . . . . . . . . .
6 Trigonometric Functions
6.1 Sine Function . . . . .
6.2 Cosine Function . . . .
6.3 Tangent Function . . .
6.4 Cosecant Function . .
6.5 Secant Function . . . .
6.6 Cotangent Function . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
7 Inverse Trigonometric Functions
7.1 Inverse Sine Function . . . . . .
7.2 Inverse Cosine Function . . . .
7.3 Inverse Tangent Function . . . .
7.4 Inverse Cosecant Function . . .
7.5 Inverse Secant Function . . . .
7.6 Inverse Cotangent Function . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . . . . . . . . .
. . . . . . . . . .
. . . . . . . . . .
Radian Measure
. . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
105
105
106
109
110
111
.
.
.
.
.
.
125
125
135
139
147
150
152
.
.
.
.
.
.
155
158
160
161
165
166
167
8 Basic Trigonometric Equations
169
8.1 Solving the Sine Equation . . . . . . . . . . . . . . . . . . . . . . . . . . . 169
8.2 Solving the Cosine Equation . . . . . . . . . . . . . . . . . . . . . . . . . . 173
8.3 Solving the Tangent Equation . . . . . . . . . . . . . . . . . . . . . . . . . 175
9 Applications: Solving a Triangle
9.1 Solving a Right Triangle . . . . . . . . . . . .
9.2 Solving Triangles that are not Right Triangles
9.3 Law of Sines . . . . . . . . . . . . . . . . . . .
9.4 Law of Cosines . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
181
182
188
190
197
4
CONTENTS
10 Applications: Area of a Triangle
203
10.1 Heron’s Formula . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 206
11 Applications: Trigonometric Identities
11.1 Basic Trigonometric identities . . . . . . . . . .
11.2 Sum and Difference Identities . . . . . . . . . .
11.3 Double-angle identities . . . . . . . . . . . . . .
11.4 Half-Angle Identities . . . . . . . . . . . . . . .
11.5 Product-to-Sum Identities . . . . . . . . . . . .
11.6 Sum-to-Product Identities . . . . . . . . . . . .
11.7 Other Trigonometric Identities and Applications
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
211
212
219
224
227
229
231
233
12 Applications: Trigonometric Equations
239
13 Applications: Circular Motion and Simple Harmonic Motion
247
14 An Introduction to Polar Coordinates
14.1 Polar Coordinate System . . . . . . . . . . . . . . . . . . .
14.2 Polar Equations and Graphs . . . . . . . . . . . . . . . . .
14.3 Relationships between Polar and Rectangular Coordinates
14.4 Selecting a Unique Pair of Polar Coordinates for a Point .
.
.
.
.
251
252
255
258
260
.
.
.
.
.
263
267
267
268
269
271
.
.
.
.
275
278
279
280
287
15 An Introduction to Complex Plane
15.1 Polar Form of a Complex Number . . . . . . . . .
15.2 Multiplication of complex numbers in Polar Form
15.3 Division of complex numbers in Polar Form . . .
15.4 Integer Powers of complex numbers in Polar Form
15.5 Distinct Complex nth roots of a Complex Number
16 An Introduction to Vectors
16.1 Vector Addition . . . . . . . . . . . .
16.2 Scalar Multiplication of a Vector . . .
16.3 Algebraic Representation of a Vector
16.4 Dot Product Between Two Vectors .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . . . .
. . . . .
. . . . .
. . . . .
in Polar
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . . .
. . . .
. . . .
. . . .
Form
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Part I
Algebra
5
Chapter 1
Equations and Inequalities
1.1
Quadratic Equations
I will assume that you have learned how to factor a polynomial, (if possible), in a prior
course. In this section, we want to make sure you know how to solve a quadratic equation
by completing the square.
Given any real number a, either a > 0, or a = 0, or a < 0. This is known as the
Trichotomy Law of real numbers.
Recall the following claim that you may have learned in high school.1
Zero Product Property Theorem. If A and B are real numbers and AB = 0,
then either A = 0 or B = 0.
Proof. Assume both A and B are not zero. Then by the Trichotomy Law for real numbers,
A > 0 or A < 0 and B > 0 or B < 0. If A and B have the same sign, then AB > 0. But
this contradicts the fact that AB = 0. Therefore, A and B cannot have the same sign. If
A and B have opposite signs, then AB < 0. This too contradicts that fact that AB = 0.
That is, A and B cannot have opposite signs either. That means our assumption must
be false. That is, by the Trichotomy Law, if AB = 0, then either A = 0 or B = 0.
1
Usually, a claim that you can prove is called a theorem.
7
8
CHAPTER 1. EQUATIONS AND INEQUALITIES
The following is another theorem that you can prove using the Trichotomy Law for real
numbers.
Squares are Nonnegative Theorem. If x is a real number, then x2 ≥ 0.
Exercise. Prove the Squares are Nonnegative Theorem.
You may have learned in high school that we sometimes use English letters to represent
numbers. (You have seen this practice in the two previous theorems.) If a letter represents
a number that can be chosen from a (finite or infinite) range of numbers, then we say
that letter represents a variable. If a letter represents a fixed number, then we say that
letter represents a constant. Historically, letters x, y, z are used to represent variables,
and letters a, b, and c are used to represent constants.
If an equation in x is a true statement for all possible values of x, then it is known as
an identity in x. The following are three important identities that you may have seen in
high school.
Three Identities Theorem. Suppose a is any positive constant and x is any real
number. Then
√
√
√
1. x2 − ( a)2 = (x − a)(x + a)
2. (x + a)2 = x2 + 2ax + a2
3. (x − a)2 = x2 − 2ax + a2
Exercise. Prove the above theorem.
The first identity is known as the Difference of Squares Identity, and the other two are
known as Binomial Square Identities.
Usually an equation in x is not a true statement for most – or even for all –values of x.
An equation in variable x is considered as an invitation to find the values of x that make
the given equation a true statement. For example, x2 = 4 is an equation in x, where x is
a real number. That is, x can be any real number. For example, 12 is a real number. But
1.1. QUADRATIC EQUATIONS
9
1 2
2
6 4. Therefore, the equation is not a true statement when x = 12 . In fact, the given
=
equation is not true for a lot of real numbers. In this case, you might be able to guess
that x has to be either 2 or −2 for the given equation to be a true statement. We say 2
and −2 are the solutions of the equation x2 = 4.
Can you always guess the solutions of an equation in x? Can you guess the solutions of
the equation 345x2 − 576x − 3245 = 0? It would be nice if we could develop an algebraic
method to find solutions of quadratic equations in x.
The following is a theorem that you may have learned in K-12.
Four Properties Theorem. Suppose A, B and C are real numbers.
1.
2.
3.
4.
If
If
If
If
A = B,
A = B,
A = B,
A = B,
then A + C = B + C.
then A − C = B − C.
then AC = BC.
, provided C 6= 0..
then CA = B
C
It is very important that you understand what this theorem says and what it does not say.
Let us look at the first statement carefully. If we know that A = B, then we know that
A + C = B + C. That is, if A = B is a true statement, then we know that A + C = B + C
is also a true statement. For example, we know that 14
= 2. Therefore, by this theorem,
7
14
5678
5678
we know that 7 + 29867 = 2 + 29867 is also true. But if we do not know that A = B is
true, then none of the conclusions of this theorem may be valid, because A = B is the
requirement for all four statements.
Let us go back to the equation x2 = 4. We know that this equation is NOT true for
almost all real numbers. (By guess-and-check we discovered that x2 = 4 is true for x = 2
and x = −2.) In the following theorem we will develop a mathematical method that we
can use to find solutions of equations in x, in general.
Theorem. Prove that the only solutions of the equation x2 = 4 are 2 and −2.
Proof. Let us assume that x2 = 4 is a true statement for some real number x. In other
words, we are assuming that x2 = 4 is a TRUE statement for some number x. Then by
the Four Properties Theorem, x2 −4 = 4−4. That is, x2 −4 = 0 is a true statement. Then
10
CHAPTER 1. EQUATIONS AND INEQUALITIES
(x − 2)(x + 2) = 0 is a true statement, by the Difference of Squares Identity. Then either
x − 2 = 0 or x + 2 = 0, by the Zero Product Property Theorem. By the Four Properties
Theorem, either x = 2 or x = −2. Our whole argument is based on our assumption that
x2 = 4 is a true statement for some real number x. Therefore, we must check and see if
our assumption is in fact correct. If x = 2, then 22 = 4 is true. If x = −2, then (−2)2 = 4
is also true. Therefore, our assumption is true for both x = 2 and x = −2. That is, 2 and
−2 are solutions of x2 = 4.
In general, you can prove the following theorem using a similar argument as in the previous
theorem.
Square-root Principle Theorem. Suppose a is a positive constant. Then the solu√
√
tions of the equation x2 = a are a and − a.
Exercise. Prove the Square-root Principle Theorem.
The next theorem is a stepping stone to finding solutions of more general quadratic
equations.
Theorem. Prove that the only solutions of the equation (x − 5)2 = 4 are 5 + 2 and 5 − 2.
Proof. Let us assume that (x − 5)2 = 4 is a true statement for some real number x.
Let X = x − 5. Then our assumption becomes: X 2 = 4 is a true statement. Then by
Square-root Principle Theorem, X = 2 and X = −2 are true statements. Substituting
back, x − 5 = 2 and x − 5 = −2 are true statements. This implies that either x = 5 + 2 or
x = 5 − 2, by the Four Properties Theorem. Check and see if these numbers are solutions
of the given equation. If x = 5 + 2, then ((5 + 2) − 5)2 = 22 = 4 is true. If x = 5 − 2,
then ((5 − 2) − 5)2 = (−2)2 = 4 is true. Therefore, our assumption is correct for both
x = 5 + 2 and x = 5 − 2. That is, 5 + 2 and 5 − 2 are solutions of (x − 5)2 = 4.
In general, you can prove the following theorem using a similar argument as in the previous
theorem.
1.1. QUADRATIC EQUATIONS
11
Theorem (Theorem 1). Suppose a and b are constants and a > 0. Then the solutions
√
√
of the equation (x − b)2 = a are b + a and b − a.
Exercise. Prove Theorem 1.
Take a closer look at the Binomial Square Identities.
Suppose a is any positive constant and x is any real number. Then
1. (x + a)2 = x2 + 2ax + a2
2. (x − a)2 = x2 − 2ax + a2
In both identities, the leading coefficient of the right side of the identity is 1, and the
constant term is the square of the half of the absolute value of the coefficient of x. That is,
given the first two terms of a binomial square, we can predict the third term of the square.
In other words, given the first two terms (with leading coefficient 1), we can complete the
square by adding the square of one half of the absolute value of the coefficient of x as the
third term.
√
Theorem. Prove that the only solutions of the equation x2 − 4x − 1 = 0 are 2 + 5 and
√
2 − 5.
Proof. Assume that x2 − 4x − 1 = 0 is a true statement for some real number x. Then by
the Four Properties Theorem, x2 − 4x = 1 is true. On the left side of this true statement
we have two terms. The first term is x2 with coefficient 1, and the second term is −4x
with coefficient −4. As we observed earlier, we can complete the square of the left side
by adding half of the absolute value of −4 square to left side. However, this will make
the given true statement false. We can use the Four Properties Theorem, and add (2)2
to both sides, and get a new true statement from the existing true statement. Therefore,
x2 − 4x + (2)2 = 1 + (2)2 is true. By recognizing the square on the left side (according
to the second binomial square identity above), (x − 2)2 = 5 is true. It should be clear at
this point why we wanted to complete the square. As you can see, by doing so we have
converted the given equation in to an equation of the form given in Theorem 1. That
√
is, at this point we can use the full force of Theorem 1. By Theorem 1, x = 2 + 5
√
√
and x = 2 − 5. Let us check and see if our assumption is true. If x = 2 + 5,
√
√
√
√
then x2 − 4x − 1 = (2 + 5)2 − 4(2 + 5) − 1 = (4 + 4 5 + 5) − 8 − 4 5 − 1 = 0.
12
CHAPTER 1. EQUATIONS AND INEQUALITIES
√
√
Therefore, our assumption is true when x = 2 + 5. If x = 2 − 5, then x2 − 4x − 1 =
√
√
√
√
(2 − 5)2 − 4(2 − 5) − 1 = (4 − 4 5 + 5) − 8 + 4 5 − 1 = 0. Therefore, our assumption
√
√
is also true when x = 2 − 5. That is, the solutions of x2 − 4x − 1 = 0 are 2 + 5 and
√
2 − 5.
√
Theorem. Prove that the only solutions of the equation 3x2 − 12x − 3 = 0 are 2 + 5
√
and 2 − 5.
Proof. Assume that 3x2 − 12x − 3 = 0 is a true statement for some real number x. Then
by using the fourth property of the Four Properties Theorem, x2 − 4x − 1 = 0 is true.
Then by the previous theorem, the result follows. [Do not forget to check your answers
with the given equation to see if your assumption is true.]
1.2
Rational Equations
Solutions to any rational equation can be found by using the method demonstrated in the
following example.
Theorem. The only solution of the equation
x
2
−4
−
= 2
is 2.
x+1 x−1
(x − 1)
Proof. First, we recognize that the given equation is the same as
2
−4
x
−
=
,
x+1 x−1
(x + 1)(x − 1)
by using the Difference of Squares Identity.
Assume that
x
2
−4
−
=
x+1 x−1
(x + 1)(x − 1)
is true for some real number x.
Then by using the third property of the Four Properties Theorem, we multiply both sides
by (x − 1)(x + 1). That is,
x
2
−4
(x − 1)(x + 1)
−
= (x − 1)(x + 1)
,
x+1 x−1
(x + 1)(x − 1)
is true.
1.2. RATIONAL EQUATIONS
13
By using the distributive property,
x
2
−4
(x − 1)(x + 1)
− (x − 1)(x + 1)
= (x − 1)(x + 1)
,
(x + 1)
(x − 1)
(x + 1)(x − 1)
is true.
By using the multiplicative inverse property, (A ·
A)2
1
A
= 1, for any non-zero real number
1 · x(x − 1) − 1 · 2(x + 1) = 1 · (−4)
is true.
By using the multiplicative identity property, (A · 1 = A, for any real number A),
x(x − 1) − 2(x + 1) = −4
is true.
By using the distributive property and collecting like terms, we have
x2 − 3x − 2 = −4
is true.
By using the Four Properties Theorem, we get
x2 − 3x + 2 = 0
is true.
By factoring the left side of the above equation,
(x − 1)(x − 2) = 0
is true.
Then by using the Zero Product Property Theorem,
x − 1 = 0 or x − 2 = 0.
2
You should have learned both the multiplicative inverse property and the multiplicative identity
property in K-12.
14
CHAPTER 1. EQUATIONS AND INEQUALITIES
By using the Four Properties Theorem again, we have narrowed down the possible solutions to just two numbers, namely
x = 1 or x = 2.
The above two statements are true only under our assumption that the given statement
is true for some number x. So, we must check if these results agree with our assumption.
When x = 1, we run into the problem of division by zero. That is, the given equation is
meaningless when x = 1 and therefore, cannot be true. Therefore 1 is not a solution of
the given equation.
When x = 2,
the left side of the equation =
2
2+1
−
and the right side of the equation =
2
2−1
=
−4
(22 −1)
2
3
− 2 = − 34 ,
= − 43 .
Therefore, 2 is a solution of the given equation.
1.3
Radical Equations
You may have seen the following theorems in K-12.
Theorem. Suppose a, b are real numbers. If a = b, then a2 = b2 .
Proof. It is given that a = b. Then by the Four Properties Theorem, a · a = a · b. That
is, a2 = ab. Since a = b, we can replace the a on the right side of the equation by b.
Therefore, a2 = b2 .
Theorem. Suppose a, b are real numbers. If a = b, then a3 = b3 .
Proof. It is given that a = b. Then by the previous theorem a2 = b2 . By the Four
Properties Theorem, a · a2 = a · b2 . That is a3 = ab2 . Since a = b, we can replace the a
on the right side of the equation by b. Therefore, a3 = b3 .
1.3. RADICAL EQUATIONS
15
Now it should be easy to see why the following theorem is true.
Theorem (Theorem 2). Suppose a, b are real numbers and n is a positive integer so
that n ≥ 2. If a = b, then an = bn .
Solutions to any rational equation can be found by using the method demonstrated in the
following theorem.
√
√
Theorem. The only solution of the equation 3x + 3 + x + 2 = 5 is 2.
√
√
Proof. Suppose 3x + 3 + x + 2 = 5 is true for some real number x. Then by the Four
Properties Theorem,
√
3x + 3 = 5 −
√
x+2
is true. Then by Theorem 2,
√
√
( 3x + 3)2 = (5 − x + 2)2
is true. Then by using the Binomial Square Identity on the right side,
√
√
3x + 3 = 52 − 2(5) x + 2 + ( x + 2)2
is true. That is,
√
3x + 3 = 25 − 10 x + 2 + x + 2
is true. Then by the Four Properties Theorem and by collecting like terms,
√
2x − 24 = −10 x + 2
is true. We can divide both sides by 2 by using the Four Properties Theorem, just to get
a slightly less complicated equation. That is,
√
x − 12 = −5 x + 2
is true. By using Theorem 2,
√
(x − 12)2 = (−5 x + 2)2
16
CHAPTER 1. EQUATIONS AND INEQUALITIES
is true. That is,
x2 − 24x + 144 = 25(x + 2)
is true. By using the Four Properties Theorem and collecting like terms,
x2 − 49x + 94 = 0
is true. By using the Four Properties Theorem,
x2 − 49x = −94
is true. By completing the square,
2
x − 49x +
2
2
49
2
2025
49
or x =
−
4
2
r
49
2
= −94 +
is true. That is,
49
x−
2
2
=
2025
4
is true. By theorem 1,
49
+
x=
2
r
2025
.
4
That is,
x = 47 or x = 2.
√
√
These results are obtained by making the assumption that 3x + 3 + x + 2 = 5 is a
true statement. Therefore, we must check and see if our assumption is true.
p
√
√
√
If x = 47, then the left side of the equation is 3(47) + 3 + 47 + 2 = 144 + 49 =
12 + 7 = 19. However, the right side is 5. Therefore, 47 is not a solution of the equation.
p
√
√
√
If x = 2, then the left side of the equation is 3(2) + 3 + 2 + 2 = 9 + 4 = 3 + 2 = 5.
Therefore, 2 is a solution of the equation.
1.4. EQUATIONS THAT CAN BE WRITTEN AS QUADRATIC EQUATIONS
1.4
17
Equations That can be Written as Quadratic
Equations
√
We know that x2 − 2x − 3 = 0 is a quadratic equation in x. Similarly, we say ( x)2 −
√
√
2 x − 3 = 0 is a quadratic equation in x. We say (x2 )2 − 2x2 − 3 = 0 is a quadratic
equation in x2 . We say (2x + 1)2 − 2(2x + 1) − 3 = 0 is a quadratic equation in 2x + 1.
We know how to solve a general quadratic equation by completing the square. Therefore,
if we can identify an equation as a quadratic equation, then we know how to solve it. The
following example demonstrates the method of finding the solutions of those equations.
√
Example. Find the solutions of the equation x − 2 x − 3 = 0.
√
Solution. Once again we will assume that x − 2 x − 3 = 0 is true for some real number
x. (A good student should realize that x ≥ 0 to begin with.) Notice that the given equation
√
√
√
can be written as ( x)2 − 2 x − 3 = 0. Therefore, it is a quadratic equation in x. If
√
we let u = x, then the given equation is u2 − 2u − 3 = 0. Then either by completing
the square or by factoring, we can show that the solutions of u2 − 2u − 3 = 0 are u = 3
√
√
and u = −1. That means x = 3 or x = −1. At this point you should realize that the
√
√
second possibility, that is, x = −1, is not valid since x ≥ 0 for any non-negative real
number x. By using Theorem 2 on the first possibility, x = 9. Now we check and see if
√
our assumption is true. If x = 9, then 9 − 2 9 − 3 = 9 − 2(3) − 3 = 0. Therefore, the
√
only solution of x − 2 x − 3 = 0 is 9.
1.5
Absolute-Value Inequalities
Students may have seen how to solve absolute value inequalities by algebraic methods in
K-12. However, the following geometric method is visually superior and will help students
understand the definition of a limit of a function when they take calculus.
Solving an inequality in x means finding all numbers x that would make the given inequality true. For example, the inequality x ≥ 2 is true for all numbers x greater than or
equal to 2. Therefore, we usually write the solutions of inequalities in interval notation.
That is, the solutions of the inequality x ≥ 2 are given by the interval [2, ∞).
18
CHAPTER 1. EQUATIONS AND INEQUALITIES
Definition. For any real number x, the absolute value of x, denoted by |x| is:
x
if x ≥ 0
|x| =
−x if x < 0
You can remember this definition as follows: To get the absolute value of a number x, if
x is positive or 0, then keep it. if x is negative, then change the sign.
The method described in the following example demonstrates how to solve an absolute
value inequality geometrically.
One Dimensional Distance Formula Theorem. Let x and a be two real numbers.
Then the distance between x and a on the number line is |x − a|.
Exercise. Prove the One Dimensional Distance Formula Theorem.
We will use the One Dimensional Distance Formula Theorem to solve absolute value
inequalities.
Example. Solve |x − 2| < 3. (“Solve” means “find the solutions of ”.)
Solution. By the One Dimensional Distance Formula Theorem, we can restate the given
inequality by translating it into everyday English.
We want “all values of x so that the distance between x and 2 is less than 3 units.”
We do not know what (number or numbers) x will satisfy this claim (yet). But we could
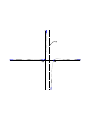
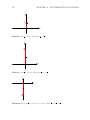
plot the point 2 on a number line as follows.
2
Furthermore, we know that x should lie within 3 units from 2. So we will identify two
points 3 units from 2 as follows.
1.5. ABSOLUTE-VALUE INEQUALITIES
3
19
3
−1
2
5
The three points −1, 2 and 5 partition the line into the intervals (−∞, −1), (−1, 2), (2, 5),
(5, ∞) and the points −1, 2 and 5. (All these sets have no points in common.)
33
Now we check each of these sets for the location of x to see if the given inequality is true.
If x is in (−∞, −1), then the distance between x and 2 is more than 3. See the following
picture.
3
3
−1
2
5
x
If x is in (−1, 2), then the distance between x and 2 is less than 3. See the following
picture.
33
3
3
−1
2
5
x
If x is in (2, 5), then the distance between x and 2 is less than 3. See the following picture.
3
3
33
−1
2
5
x
If x is in (5, ∞), then the distance between x and 2 is more than 3. See the following
picture.
33
3
3
−1
2
5
x
If x = −1, then the distance between x and 2 is 3. See the following picture.
33
20
CHAPTER 1. EQUATIONS AND INEQUALITIES
3
3
2
5
x = −1
If x = 2, then the distance between x and 2 is 0 (less than 3). See the following picture.
3
3
33
−1
5
x=2
If x = 5, then the distance between x and 2 is 3. See the following picture.
3
3
33
−1
2
x=5
Now we will highlight the intervals, based on our observations, where the given inequality
is true.
33
−1
5
Therefore, if x is in the interval (−1, 5), then the inequality is true. Therefore, the solutions of the inequality lie in the open interval (−1, 5). We loosely say, the solution is the
interval (−1, 5).
You may have learned the following theorem on inequalities in K-12.
Theorem (Theorem 3). Suppose a, b and c are real numbers.
1. If a > b, then a + c > b + c.
2. If a > b, then ac > bc, if c > 0.
3. If a > b, then ac < bc, if c < 0.
You may have learned the following theorem on inequalities in high school.
Theorem (Theorem 4). If a and b are real numbers, then |ab| = |a||b|.
1.6. QUADRATIC FORMULA
21
Exercise. Prove Theorem 4.
With the help of Theorems 3 and 4, we can find the solutions of slightly more complicated
absolute value inequalities.
Example. Solve |4x − 8| < 12.
Solution. The left side of the given inequality is the same as |4(x−2)|, by the distributive
law. Then by Theorem 4, this is the same as |4||x − 2|. But |4| = 4, by definition.
Therefore, the given inequality can be written as 4|x−2| < 12. By Theorem 3, if 4|x−2| <
12 is true, then |x − 2| < 3 is true. (Multiply both sides by 41 .) Also, by the same theorem,
if |x − 2| < 3 is true, then 4|x − 2| < 12 is true. (Multiply both sides by 4.). Therefore,
if we can find the solutions of |x − 2| < 3, then they will be the solutions of 4|x − 2| < 12
and vice versa. At this point, you will use the geometric method that you learned in the
previous example to solve |x − 2| < 3.
1.6
Quadratic Formula
Since by now students have had plenty of practice with completing the square and are
familiar with that method, this should be a good time to prove the Quadratic Formula
Theorem for real numbers.
Quadratic Formula Theorem. Suppose a 6= 0, b, and c are fixed real numbers
(constants), and x is any real number. Then the solutions of the equation ax2 +bx+c =
0 are
√
√
−b + b2 − 4ac
−b − b2 − 4ac
and
, provided b2 − 4ac ≥ 0.
2a
2a
2
If b − 4ac = 0, then the two solutions are equal.
Convention: It is customary to write the two solutions together as
−b ±
Proof. Suppose ax2 + bx + c = 0 is true for some real number x. Then
b
c
x2 + x + = 0
a
a
√
b2 − 4ac
.
2a
22
CHAPTER 1. EQUATIONS AND INEQUALITIES
is true. Then
b
c
x2 + x = −
a
a
is true. By completing the square,
2
2
b
b
c
b
2
x + x+
=− +
a
2a
a
2a
is true. That is,
2
b2 − 4ac
b
=
x+
2a
4a2
is true. That means
2
b
b2 − 4ac
=0
x+
−
2a
4a2
is true. Then
√ 2
√ 2
b − 4ac
b
b − 4ac
b
+
x+
−
=0
x+
2a
2a
2a
2a
is true, provided b2 − 4ac ≥ 0, by using the Difference of Squares identity. That is,
√
√
b
b2 − 4ac
b
b2 − 4ac
x− − −
x− − +
=0
2a
2a
2a
2a
is true. Now, by the Zero Product Property Theorem,
√
√
−b + b2 − 4ac
−b − b2 − 4ac
x=
or x =
2a
2a
Now we check and see if our assumption is true for these numbers.
√
−b − b2 − 4ac
If x =
, then
2a
√
√
2
−b − b2 − 4ac
−b − b2 − 4ac
2
ax + bx + c = a
+b
+c
2a
2a
2
√
√
1
2
= 2 a −b − b2 − 4ac + 2ab −b − b2 − 4ac + 4a c
4a
i
√
√
1 h = 2 a b2 + 2b b2 − 4ac + b2 − 4ac + 2ab −b − b2 − 4ac + 4a2 c
4a
1.6. QUADRATIC FORMULA
23
i
√
√
1 h 2
2 − 4ac + ab2 − 4a2 c − 2ab2 − 2ab b2 − 4ac + 4a2 c
ab
+
2ab
b
4a2
1
= 2 [0]
4a
=0
√
−b − b2 − 4ac
is a solution of ax2 + bx + c = 0.
Therefore, x =
2a
The way of checking the other solution is similar: you should be able to verify that
√
−b + b2 − 4ac
x=
is also a solution of ax2 + bx + c = 0.
2a
=
Note 1 The proof of the previous theorem is valid only if b2 − 4ac ≥ 0. This is because
√
b2 − 4ac has no real meaning when b2 − 4ac < 0. If b2 − 4ac < 0, then the equation
has no real solutions.
b
Note 2 If b2 − 4ac = 0, then both solutions are the same. In this case, the solution is − 2a
.
Note 3 The Quadratic Formula Theorem can be used to factor3 quadratic polynomials
rather quickly.
Suppose a is a positive whole number and b and c are integers. We want to factor
ax2 + bx + c so that the resulting linear factors are of the form rx + s, where r is a
positive integer and s is an integer.
Let d2 = b2 − 4ac. Calculate d2 . If d2 is negative or if d2 is not a perfect (whole
number) square, then the given trinomial is not factorable.
If d2 is a perfect square, then pick the square-root of d2 as d. For example, if d2 = 16,
(−b−d)
then pick d = 4. Then, compute (−b+d)
and (−b−d)
. If (−b+d)
are integers,
2a 2a 2a
2a and then the factors of the trinomial are x −
(−b+d)
2a
and x −
(−b−d)
2a
.
If (−b+d)
and (−b−d)
are rational numbers, then suppose (−b+d)
= k` and (−b−d)
=m
2a
2a
2a
2a
n
in reduced form, where ` and n are whole numbers. Then (`x − k) and (nx − m)
are the factors of the trinomial.
For example, if you wish to factor 6x2 − 4x + 5, then b2 − 4ac = 16 − 4(6)(5) < 0.
Therefore, 6x2 − 4x + 5 cannot be factored. If you wish to factor 6x2 − 4x − 5,
3
Here “factor” means factoring over the integers just like in high school. That is, the coefficients of
the factors are integers. For example x2 − 4 is factorable over the integers as (x − 2)(x + 2), but x2 − 3
is not factorable over the integers.
24
CHAPTER 1. EQUATIONS AND INEQUALITIES
then b2 − 4ac = 16 + 4(6)(5) = 136. But 136 is not a perfect square. Therefore,
6x2 − 4x − 5 is not factorable either. If you wish to factor 6x2 − 5x − 6, then
b2 − 4ac = 25 + 4(6)(6) = 169. This is a perfect square, and d = 13. Then, −b+d
= 32
2a
= −2
in reduced form. Therefore, the factors are (2x − 3) and (3x + 2).
and −b−d
2a
3
i
h
√
2 −4ac
b
− b 2a
and
Note 4 If we are interested in factoring over real numbers, then x − − 2a
h
i
√
2 −4ac
b
x − − 2a
are factors of ax2 − bx + c, if b2 − 4ac > 0.
+ b 2a
Note 5 Since b2 − 4ac is such an important quantity for a given quadratic polynomial ax2 +
bx + c, we will call it the discriminant of ax2 + bx + c.
Note 6 If the discriminant of a polynomial ax2 + bx + c is negative, then the number ax2 +
bx + c 6= 0 for any real number x. That means, according to the Trichotomy Law
for real numbers, ax2 + bx + c is either positive or negative for any real x.
We can do better with the use of following two properties of real numbers.
If a is a real number, then a + 0 = a. This is known as the Additive Identity
Property for real numbers.
If a is a real number, then a + (−a) = 0. This is known as the Additive Inverse
Property for real numbers.
By using the above two properties and completing the square, we can write ax2 +
bx + c in an equivalent form that sheds more light onto the collection of numbers
ax2 + bx + c, for all real numbers x.
c
by the distributive property.
a
c
+0
by the additive identity property.
a
2 2 !
b
c
b
b
2
=a x + x+ +
−
by the additive inverse property.
a
a
2a
2a
b
ax + bx + c = a x + x +
a
b
= a x2 + x +
a
2
2
1.7. POLYNOMIAL AND RATIONAL INEQUALITIES
25
2 !
2 !
b
b
c
b
=a
x2 + x +
+ −
a
2a
a
2a
2
b
b2
=a x+
+c−
by the distributive property.
2a
4a
2
b
4ac − b2
=a x+
+
2a
4a
b 2
By the Squares are Nonnegative Theorem, x + 2a
≥ 0. That is, if a > 0, then
b 2
the smallest value of a x + 2a is 0. If a < 0, then by Theorem 3, part 3, the
b 2
is 0.
largest value of a x + 2a
2
Observe that 4ac−b
is a constant. Therefore, if a > 0, then the smallest value of
4a
2
4ac−b2
2
ax + bx + c is 4a , and if a < 0, then the largest value of ax2 + bx + c is 4ac−b
.
4a
2
> 0. That is, the smallest value of
Suppose a > 0 and b2 − 4ac < 0. Then 4ac−b
4a
2
2
ax + bx + c is positive. Since ax + bx + c 6= 0, this means that ax2 + bx + c > 0
for all x.
2
Suppose a < 0 and b2 − 4ac < 0. Then 4ac−b
< 0. That is, the largest value of
4a
ax2 + bx + c is negative. Since ax2 + bx + c 6= 0, this means that ax2 + bx + c < 0
for all x.
1.7
Polynomial and Rational Inequalities
We will assume that one side of the inequality is 0. We will also assume that any polynomial of degree greater than 2 in a polynomial or rational inequality is factorable. In
other words, we will look only at factorable inequalities where one side is equal to 0. The
method demonstrated in the following example can be used for those types of inequalities.
Example. Solve
(x2 − x + 1)(x − 2)2 (x + 3)
≤ 0,
x2 − 3
if possible.
Solution. We will again use a geometrical argument to solve this inequality. First, we
want to make sure the rational expression on the left side is completely factored over the
reals. The polynomial x2 − x + 1 is not factorable because the discriminant is negative.
26
CHAPTER 1. EQUATIONS AND INEQUALITIES
We say such a quadratic polynomial irreducible over the reals. However, x2 − 3 can be
√
√
factored using the Difference of Squares identity into (x − 3)(x + 3). Therefore, the
given inequality can be written as:
(x2 − x + 1)(x − 2)2 (x + 3)
√
√
≤0
(x − 3)(x + 3)
The left side is a product (or quotient) of linear polynomials or irreducible quadratic
polynomials. By the Trichotomy Law for real numbers, each polynomial as a number is
either positive, negative or zero. The points where each polynomial is equal to zero are
√
√
called the critical points of the inequality. In this case, 2, −3, 3 and − 3 are the critical
points. Mark those critical points on a number line as shown below.
−3
√
− 3
√
3
2
We have found the points where each linear polynomial is zero. For example, x − 2 is
zero when x = 2. So, for all other points on the number line, x − 2 is either positive or
negative. When x < 2, by Theorem 3, x − 2 < 0 and when x > 2, by the same theorem,
x − 2 > 0. We can include this information below the same number line as follows.
√
√
−3
2
− 3
3
x − 2 :− − − − − − − − − − − − − − − − − − −− 0 + + + + +
In a similar way, x + 3 < 0 when x < −3 and x + 3 > 0 when x > −3.
√
√
−3
2
− 3
3
x − 2 :− − − − − − − − − − − − − − − − − − −− 0 + + + + +
x + 3 :−− 0 + + + + + + + + + + + + + + + + + + + + + + +
√
√
√
√
√
(x − 3) < 0 when x < 3 and (x − 3) > 0 when x > 3. Also, (x + 3) < 0 when
√
√
√
x < − 3 and (x + 3) > 0 when x > − 3.
1.7. POLYNOMIAL AND RATIONAL INEQUALITIES
27
√
√
−3
2
− 3
3
x − 2 :− − − − − − − − − − − − − − − − − − −− 0 + + + + +
x + 3 :−− 0 + + + + + + + + + + + + + + + + + + + + + + +
√
x − √3 :− − − − − − − − − − − − − − − 0+ + + + + + + + +
x + 3 :− − − − −− 0+ + + + + + + + + + + + + + + + + + +
The discriminant of the (irreducible) quadratic factor x2 −x+1 is negative and the leading
coefficient is positive. Therefore, by Note 6 following the Quadratic Formula Theorem,
x2 − x + 1 > 0 for all x.
√
√
−3
2
− 3
3
x−2:
− − − − − − − − − − − − − − − − − − −−0 + + ++
−− 0 + + + + + + + + + + + + + + + + + + + + ++
x+3:
√
− − − − − − − − − − − − − − −− 0 + + + + + + + + +
x − √3 :
− − − − −− 0+ + + + + + + + + + + + + + + + ++
x+ 3:
2
x − x + 1 : + + + + + + + + + + + + + + + + + + + + + + + + ++
√
The critical points partition the number line into the intervals (−∞, −3), (−3, − 3),
√ √
√
√ √
(− 3, 3), ( 3, 2), (2, ∞), and the points −3, − 3, 3, 2. We will check and see if the
given inequality is true in these sets.
In (−∞, −3), four of the five factors are negative and one factor is positive. Therefore,
the left side of the given inequality is positive.
√
In (−3, − 3), three of the five factors are negative and two factors are positive. Therefore,
the left side of the given inequality is negative.
√ √
In (− 3, 3), two of the five factors are negative and three factors are positive. Therefore,
the left side of the given inequality is positive.
√
In ( 3, 2), one of the five factors is negative and four factors are positive. Therefore, the
left side of the given inequality is negative.
In (2, ∞), all five factors are positive. Therefore, the left side of the given inequality is
positive.
At −3, the left side of the inequality is 0.
28
CHAPTER 1. EQUATIONS AND INEQUALITIES
√
At − 3, the left side of the inequality is undefined.
√
At 3, the left side of the inequality is undefined.
At 2, the left side of the inequality is 0.
Putting all this information together, we see that the given inequality is true for the intervals shown in the following figure.
√
√
−3
2
− 3
3
x−2:
− − − − − − − − − − − − − − − − − − −−0 + + ++
−− 0 + + + + + + + + + + + + + + + + + + + + ++
x+3:
√
− − − − − − − − − − − − − − −− 0 + + + + + + + + +
x − √3 :
− − − − −− 0+ + + + + + + + + + + + + + + + ++
x+ 3:
2
x − x + 1 : + + + + + + + + + + + + + + + + + + + + + + + + ++
√ S√
Therefore, the solution to the given inequality is (−3, − 3] ( 3, 2].
Chapter 2
Graphs of Polynomial and Rational
Functions
2.1
Graphs of Quadratic Functions
Given a (real-valued) function f , the collection of all points (x, f (x)), for each point x in
the domain of f is called the graph of f .
We will assume that you know the definition of a real-valued function. We will also assume
that you have sketched graphs of basic functions such as linear functions, f (x) = x2 ,
f (x) = x3 , f (x) = |x|, and f (x) = x1 by using several well-chosen points on the graph by
creating tables.
In this section, we will sketch the graphs of quadratic functions by looking at attributes
we will call “the end behavior”, “the zeros”, and “the vertex”.
The behavior of the function for very large values of x or very small values of x is called
the end behavior . We indicate “very large values of x” by using the symbols x → ∞ and
“very small values of x” by using the symbols x → −∞.
A value of x at which f (x) = 0 is called a zero of f .
A point on the graph of a quadratic equation at which the f has the smallest value or the
largest value is called the vertex of the graph of the quadratic function f .
Our options are limited when comes to graphs in Precalculus. The concepts of continuity,
increasing, decreasing, and concavity are not available. Therefore, our approach here will
be to rely on some known properties of graphs of a few known functions to sketch the
29
30
CHAPTER 2. GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
graphs of more sophisticated functions. Our motto will be not to add any extra wiggles
or extra turns or introduce gaps or holes to a graph without providing a reason. With
that in mind we will start with basic quadratic functions.
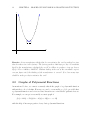
Example. Sketch the graph of f (x) = x2 .
Solution. End behavior:
For x → ∞, f (x) = x2 → ∞. (For large values of x, x2 is large.)
For x → −∞, f (x) = x2 → ∞. (For −(large values of x), x2 is large.)
Zeros:
f (x) = 0 when x = 0. Therefore, 0 is the zero of f .
Vertex:
We know that x2 ≥ 0, for any real number x. Therefore, f has the smallest value when
x = 0. That is, (0, f (0)) is the point on the graph where f is minimum. That is, (0, 0) is
the vertex.
Now sticking to our declared motto of not adding any extra wiggles or extra turns or
introducing gaps or holes to a graph without providing a reason, (and also relying on past
experience), we will sketch the graph of f (x) = x2 .
y
The end behavior
x
The behavior near zero
By going through the same analysis, that is, finding the end behavior, finding the zero,
finding the vertex, and sketching the graph following our established motto, you will see
that the graph of g(x) = ax2 , where a is a positive constant, is similar to the graph of
f (x) = x2 .
2.1. GRAPHS OF QUADRATIC FUNCTIONS
Therefore, we say graphs of f1 (x) = x2 , f2 (x) =
shape”.
31
13 2
x,
245
f3 (x) = 4672x2 have the “same
Example. Sketch the graph of f (x) = −x2 .
Solution. End behavior:
For x → ∞, f (x) = −x2 → −∞.
For x → −∞, f (x) = x2 → −∞.
Zeros:
f (x) = 0 when x = 0. Therefore, 0 is the zero of f .
Vertex:
We know that −x2 ≤ 0, for any real number x. Therefore, f has the largest value when
x = 0. That is, (0, f (0)) is the point on the graph where f is maximum. That is, (0, 0) is
the vertex.
The graph of f (x) = −x2 is given below.
y
x
The graph of g(x) = ax2 , where a is a negative constant, is similar to the graph of
f (x) = −x2 .
Example. Sketch the graph of f (x) = 234(x − 57)2 .
Solution. End behavior:
For x → ∞, that is, for large x, f (x) ≈ 234x2 . (You can think of this in terms of money.
32
CHAPTER 2. GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
Suppose x is one billion dollars. (Bill Gates has more than one billion dollars.) Now, if
you subtract 57 dollars from a billion dollars, then the remaining number, for all practical
purposes, is still roughly a billion dollars. If Bill Gates misplaces 57 dollars, he may
not even notice it.) Therefore, the end behavior of f is the same as the end behavior of
g(x) = ax2 , where a is a positive constant.
Zeros:
f (x) = 0 when x = 57. Therefore, 57 is the zero of f .
Vertex:
We know that (x − 57)2 ≥ 0, for any real number x. Therefore, f has the smallest value
when x = 57. That is, (57, f (57)) is the point on the graph where f is minimum. That
is, (57, 0) is the vertex.
The graph of f (x) = 234(x − 57)2 is given below.
y
(57, 0)
x
The graph of g(x) = a(x−h)2 , where a is a positive constant and h is a constant, is similar
to the graph of f (x) = 234(x − 57)2 . That is, the graphs of f1 (x) = 2465
(x − (−48))2 ,
345
f2 (x) = 973(x − 6893)2 have the “same shape” as the graph of f (x) = 234(x − 57)2 .
Similar analysis leads to the following graph of the function f (x) = a(x − h)2 , where a is
a negative constant and h is a constant.
2.1. GRAPHS OF QUADRATIC FUNCTIONS
33
y
(h, 0)
x
Example. Sketch the graph of f (x) = 3481(x − 545)2 + 38.
Solution. End behavior:
For x → ∞, f (x) ≈ 3481x2 . (For large x, x−545 ≈ x and then for large x, 3481x2 +38 ≈
3481x2 .) Therefore, the end behavior of f (x) = 3481(x − 545)2 + 38 is the same as the
end behavior of g(x) = 3481x2 .
Vertex:
We know that (x − 545)2 ≥ 0, for any real number x. Therefore, f has the smallest value
when x = 545. That is, (545, f (545)) is the point on the graph where f is minimum. That
is, (545, 38) is the vertex.
zeros:
If for some x, f (x) = 0, then 3481(x − 545)2 + 38 = 0. But this is impossible because
the left side of this equation is positive for any real number x. Therefore, the equation,
3481(x − 545)2 + 38 = 0, has no solutions. (This is an instance where the skills developed
in solving quadratic equations are helpful.) That is, f has no zeros.
The graph of f is given below.
34
CHAPTER 2. GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
y
(545, 38)
x
The graph of g(x) = a(x−h)2 +k, where a is a positive constant and h and k are constants
is similar to the graph of f (x) = 3481(x − 545)2 + 38.
The graph of f (x) = a(x − h)2 + k, where a is a negative constant, and h and k are
constants, has a graph similar to the following graph.
y
(h, k)
x
f (x) = a(x−h)2 +k is called the standard form of a quadratic function. f (x) = ax2 +bx+c
is called the general form of a quadratic function. Based on our experience, we can
2.1. GRAPHS OF QUADRATIC FUNCTIONS
35
quickly sketch the graph of a quadratic function and identify the vertex if it is given in
the standard form. In Note 6 to the Quadratic Formula Theorem you have seen how
to convert a quadratic polynomial in general form to standard form by completing the
square.
Example. Identify the end behavior, find the vertex, find the zeros, and sketch accurately
the graph of f (x) = 32x2 − 38x + 41.
Solution.
38
41
32x − 38x + 41 = 32 x − x +
32
32
2 !
2 !
19
19
19
41
−
= 32
x2 − x +
+
16
32
32
32
2
19
192
= 32 x −
+ 41 −
32
32
2
19
951
= 32 x −
+
32
32
2
2
The end behavior:
For x → ∞, f (x) ≈ 32x2 . Therefore,
For x → ∞, f (x) → ∞.
For x → −∞, f (x) → ∞.
The vertex:
The function has the smallest value when x =
951
That is, the vertex is 19
,
.
32 32
19
.
32
Therefore, the vertex is
19
19
, f ( 32
)
32
.
2 951
If we assume that f (x) = 0 for some value of x, then we get 32 x − 19
+ 32 = 0.
32
However, the left side of this equation is positive for all real numbers x. Therefore, this
equation has no solutions. That is, this function has no zeros.
The graph of the function is:
36
CHAPTER 2. GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
y
19 951
,
32 32
x
Exercise. A toy manufacturer thinks that he can minimize the cost by making less toys
than he makes now in his factory. The factory produces 1000 toys per day. A consultant
hired by the manufacturer calculated the cost C in dollars to produce x toys per day as
C(x) = 15x2 − 29430x + 14435527. Without looking at the rest of the consultant’s report,
can you figure out if the thinking of the manufacturer is correct? If so, how many toys
should he make per day to minimize the cost?
2.2
Graphs of Polynomial Functions
As mentioned before, we cannot accurately sketch the graph of a polynomial function
without the tools of calculus. However, we can do a reasonably good job, provided that
a polynomial function can be factored into linear factors or irreducible quadratic factors.
For example, we can get a reasonably accurate graph of
f (x) = 241(x − 356)2 (32x − 43)3 (x + 41)(x2 − x + 41)
with the help of known properties of very basic polynomial functions.
2.2. GRAPHS OF POLYNOMIAL FUNCTIONS
37
With that in mind let us summarize what we have so far.
y
y
(h, 0)
(h, 0)
x
x
(a) f (x) = a(x − h)2 , where a > 0
(b) f (x) = a(x − h)2 , where a < 0
Exercise. Find the end behavior, the zero, and sketch the graph of f (x) = 24(x − 31)4 .
It is easy to see that the graph of f (x) = a(x − h)n , where n is even and a > 0, has
the same end behavior, the same zero, and the same behavior near zero as the graph of
f (x) = a(x − h)2 , where a > 0. Also, f (x) = a(x − h)n , where n is even and a < 0, has
the same end behavior, the same zero, and the same behavior near zero as the graph of
f (x) = a(x − h)2 , where a < 0. We summarize our findings in the following figure.
y
y
(h, 0)
(h, 0)
(a) f (x) = a(x − h)n , where a > 0
and n is even
x
(b) f (x) = a(x − h)n , where a < 0
and n is even
Figure 1
x
38
CHAPTER 2. GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
Now we will examine the graphs of cubic polynomials.
Example. Sketch the graph of f (x) = 217(x − 53)3 .
Solution. End behavior:
For x → ∞, f (x) ≈ 217x3 → ∞.
For x → −∞, f (x) ≈ 217x3 → −∞.
Zeros:
f (x) = 0 when x = 53. Therefore, 53 is the zero of f .
Now sticking to our motto of not adding any extra wiggles or extra turns or introducing gaps or holes to a graph without providing a reason, and definitely relying on past
experience, we will sketch the graph of f (x) = 217(x − 53)3 .
y
53
x
It is easy to see that the graphs of f (x) = a(x − h)n , where n > 3 is odd and a > 0, has
the same end behavior, the same zero, and the same behavior near zero as the graph of
f (x) = 217(x − 53)2 .
Example. Sketch the graph of f (x) = −217(x − 53)3 .
Solution. End behavior:
For x → ∞, f (x) ≈ −217x3 → −∞.
For x → −∞, f (x) ≈ −217x3 → ∞.
Zeros:
f (x) = 0 when x = 53. Therefore, 53 is the zero of f .
2.2. GRAPHS OF POLYNOMIAL FUNCTIONS
39
Now sticking to our motto of not adding any extra wiggles or extra turns or introducing gaps or holes to a graph without providing a reason, and definitely relying on past
experience, we will sketch the graph of f (x) = −217(x − 53)3 .
y
x
53
It is easy to see that the graphs of f (x) = a(x − h)n , where n > 3 is odd and a < 0 has
the same end behavior, the same zero, and the same behavior near zero as the graph of
f (x) = −217(x − 53)2 .
We summarize our findings in the following figure.
y
y
h
(a) f (x) = a(x − h)n , where a > 0
and n ≥ 3 is odd
x
h
(b) f (x) = a(x − h)n , where a < 0
and n ≥ 3 is odd
Figure 2
x
40
CHAPTER 2. GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
Surprisingly, the information in the graphs of figures 1 and 2 is sufficient to sketch the
graphs of polynomial functions that can be factored into linear factors or irreducible
quadratic factors. The method demonstrated in the following example can be used to
sketch the graphs of such polynomial functions.
Exercise. Identify the end behavior, the zeros, the behavior near each zero, and sketch
the graph of
f (x) = 241(x − 356)2 (32x + 43)3 (x + 41)(x2 − x + 41)
accurately.
Solution. On the side, write the standard from of the polynomial x2 − x + 41. This turns
2
out to be x − 21 + 163
. Now we know that x2 − x + 41 > 0 for all x. We also know that
4
x2 − x + 41 ≈ x2 for large values of x. With this additional information, we can begin
analyzing the given polynomial function.
The end behavior:
For x → ∞, f (x) ≈ 241(x2 )(323 x3 )(x)(x2 ) = 241(32)3 x8 . Therefore, f has the same end
behavior as g(x) = a(x − h)n , where a > 0 and n is even. (Here, h = 0.)
y
zeros:
43
, and x = −41. Therefore, the zeros are 356, − 32
, and
f (x) = 0, when x = 356, x = − 43
32
−41.
Now we check the behavior near each zero.
Near x = 356:
The factor 32x − 43 ≈ 32(356) + 43 > 0. Then (32x + 43)3 ≈ (32(356) − 43)3 > 0.
The factor x + 41 ≈ 356 + 41 > 0. The factor x2 − x + 41 > 0, for any x. Let a =
(32(356) + 43)3 (356 + 41)(3562 − 356 + 41). Then a > 0 and f (x) ≈ a(x − 356)2 near the
zero x = 356. Therefore, the graph of f looks like the graph of g1 (x) = a(x − 356)2 near
x = 356.
x
(356, 0)
Near x = − 43
:
32
43
The factor x − 356 ≈ (− 43
− 356) < 0. But, (x − 356)2 ≈ (− 32
− 356)2 > 0. The factor
32
2.3. GRAPHS OF RATIONAL FUNCTIONS
41
43 2
x + 41 ≈ − 43
+ 41 > 0. The factor x2 − x + 41 ≈ (− 32
) − (− 43
) + 41 > 0. Let b =
32
32
43
43 2
43
43 3
43
2
).
(32)(241)(− 32 + 356) (− 32 + 41)((− 32 ) − (− 32 ) + 41). Then b > 0 and f (x) ≈ b(x + 32
43 3
43
Therefore, the graph of f looks like the graph of g2 (x) = b(x + 32 ) near x = − 32 .
x
(− 43
, 0)
32
Near x = −41: The factor x−356 ≈ (−41−356) < 0. But, (x−356)2 ≈ (−41−356)2 > 0.
The factor 32x + 43 ≈ 32(−41) + 43 < 0 Then (32x + 43)3 ≈ (32(−41) + 43)3 < 0. The
factor x2 − x + 41 ≈ (−41)2 − (−41) + 41 > 0. Let c = 241(−41 − 356)2 (32(−41) +
43)3 ((−41)2 − (−41) + 41). Then c < 0 and f (x) ≈ c(x + 41). Therefore, the graph of f
looks like the graph of the line g3 (x) = c(x + 41), with a negative slope, near x = −41.
x
(−41, 0)
Now sticking to our motto of not introducing any extra wiggles, gaps or holes without
providing reasons, we can sketch the graph of the given function.
y
−41
2.3
43
− 32
356
x
Graphs of Rational Functions
In sketching graphs of rational functions, we will use the same method of sketching graphs
of functions based on the properties of few simple functions, just as we did with the
graphs of polynomial functions. However, there are a few additional properties that we
42
CHAPTER 2. GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
have to worry about when we are dealing with rational functions, compared to polynomial
functions. Let us start with the graph of a simple rational function.
Example. Sketch the graph of f (x) = x1 .
Solution. End Behavior:
For x → ∞, that is, for large x, f (x) = x1 is very small but remains positive. We indicate
this behavior by using a new notation: f (x) → 0+ .
For x → −∞, that is, for −(large) x, f (x) = x1 is very small but remains negative. We
indicate this behavior by using a new notation: f (x) → 0− .
Zeros:
There is no number x for which f (x) = 0. That is, this function has no zeros.
However, f is undefined at 0. We will check the behavior near 0. We want to see the
behavior to the left of 0 and the behavior to the right of 0. We introduce new notations to
indicate this behavior.
The notation x → 0− indicates that “x is to the left of 0 but very close to 0”.
The notation x → 0+ indicates that “x is to the right of 0 but very close to 0”.
Near 0:
For x → 0− , f (x) < 0 and |f (x)| is very large. We indicate this behavior by the notation
f (x) → −∞.
For x → 0+ , f (x) > 0 and |f (x)| is very large. We indicate this behavior by the notation
f (x) → ∞.
With the information we gathered on the graph of f , and with prior experience from high
school, now we can sketch the graph by remaining true to our motto.
2.3. GRAPHS OF RATIONAL FUNCTIONS
43
y
x
Exercise.
1. Show that the graph of g(x) = 341
is similar to the graph of f (x) = x1 by checking the
x
end behavior, behavior near zeros, and behavior near points where g is undefined.
2. In general, show that the graph of h(x) = xa , where a is a positive constant, is
similar to the graph of f (x) = x1 by checking the end behavior, behavior near zeros
and behavior near points where g is undefined.
The behavior of the graph of f (x) = x1 near 0 is worth identifying as a special property
of f . We say the vertical line x = 0 is a vertical asymptote of f .
In general, given a function f , if we see at least one of the following behaviors:
for x → a− , f (x) → ±∞ or or x → a+ , f (x) → ±∞,
then we say that the vertical line x = a is a vertical asymptote of f .
Example. Find the end behavior, find the zeros, and find the points where the function is
undefined. Check the behavior of the function at the points where the function has a zero
or where the function is undefined, and sketch the graph. Include any vertical asymptote
of the function on the same set of coordinates.
f (x) =
341
.
x − 23
44
CHAPTER 2. GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
Solution. End Behavior:
. Therefore, the end behavior of f is the same as the end behavior
For x → ∞, f (x) ≈ 341
x
341
of g1 (x) = x .
Zeros:
f has no zeros.
Undefined:
f is undefined at x = 23.
Behavior near x = 23:
For x → 23− , f (x) < 0 and f (x) → −∞.
For x → 23+ , f (x) > 0 and f (x) → ∞.
Therefore, the vertical line x = 23 is a vertical asymptote of f .
A sketch of the graph of f is given below. The dashed line is not part of the graph of f ;
it is the vertical asymptote x = 23. It is customary to include the graph of the vertical
asymptote with the graph of the function for clarity.
y
x
a
Exercise. Show that the graph of g(x) = x−b
, where a is a positive constant and b is a
341
constant, is similar to the graph of f (x) = x−23 by checking the end behavior, behavior near
zeros, and behavior near points where g is undefined. Show that the vertical asymptote of
g is the line x = b.
2.3. GRAPHS OF RATIONAL FUNCTIONS
45
Example. Find the end behavior, find the zeros, and find the points where the function is
undefined. Check the behavior of the function at the points where the function has a zero
or where the function is undefined, and sketch the graph. Include any vertical asymptote
of the function on the same set of coordinates.
−341
f (x) =
.
x − 23
Solution. End Behavior:
For x → ∞, f (x) ≈ −341
. For x → ∞, −341
is negative and −341
→ 0− .
x
x
x
For x → −∞, that is, for -(large) x, f (x) ≈
−341
→ 0+ .
x
−341
.
x
For x → −∞,
−341
x
is positive and
Zeros:
f has no zeros.
Undefined:
f is undefined at x = 23.
Behavior near x = 23:
For x → 23− , f (x) > 0 and f (x) → ∞.
For x → 23+ , f (x) < 0 and f (x) → −∞.
The vertical line x = 23 is a vertical asymptote of f .
A sketch of the graph of f is given below, including the vertical asymptote.
y
x
a
Exercise. Show that the graph of g(x) = x−b
, where a is a negative constant and b is a
−341
constant, is similar to the graph of f (x) = x−23 by checking the end behavior, behavior
46
CHAPTER 2. GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
near zeros and behavior near points where g is undefined. Show that the vertical asymptote
of g is the line x = b.
Example. Find the end behavior, find the zeros, and find the points where the function
is undefined. Check the behavior of the function at the points where the function has a
zero or the function is undefined, and sketch the graph. Include any vertical asymptote of
the function on the same set of coordinates.
f (x) =
341
.
(x − 23)2
Solution. End Behavior:
. For x → ∞,
For x → ∞, f (x) ≈ 341
x2
341
x2
is positive and
For x → −∞, that is, for -(large) x, f (x) ≈
341
→ 0+ .
x2
341
.
x2
341
x2
→ 0+ .
For x → −∞,
341
x2
is positive and
Zeros:
f has no zeros.
Undefined:
f is undefined at x = 23.
Behavior near x = 23:
For x → 23− , f (x) > 0 and f (x) → ∞.
For x → 23+ , f (x) > 0 and f (x) → ∞.
The vertical line x = 23 is a vertical asymptote of f .
A sketch of the graph of f is given below, including the vertical asymptote.
y
x
2.3. GRAPHS OF RATIONAL FUNCTIONS
47
a
Exercise. Show that the graph of g(x) = (x−b)
n , where a is a positive constant, b is a
constant and n is even, has the same end behavior and the same behavior near the point
341
where g is undefined as the graph of f (x) = (x−23)
2 by checking the end behavior, behavior
near zeros and behavior near points where g is undefined. Show that the vertical asymptote
of g is the line x = b.
Example. Find the end behavior, find the zeros, and find the points where the function is
undefined. Check the behavior of the function at the points where the function has a zero
or where the function is undefined, and sketch the graph. Include any vertical asymptote
of the function on the same set of coordinates.
−341
.
f (x) =
(x − 23)2
Solution. End Behavior:
. For x → ∞,
For x → ∞, f (x) ≈ −341
x2
−341
x2
is negative and
For x → −∞, that is, for -(large) x, f (x) ≈
−341
→ 0− .
x2
−341
.
x2
−341
x2
→ 0− .
For x → −∞,
−341
x2
is negative and
Zeros:
f has no zeros.
Undefined:
f is undefined at x = 23.
Behavior near x = 23:
For x → 23− , f (x) > 0 and f (x) → ∞.
For x → 23+ , f (x) > 0 and f (x) → ∞.
The vertical line x = 23 is a vertical asymptote of f .
A sketch of the graph of f is given below, including the vertical asymptote.
y
x
48
CHAPTER 2. GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
a
Exercise. Show that the graph of g(x) = (x−b)
n , where a is a negative constant, b is a
constant and n is even, has the same end behavior, same behavior near the point where
−341
g is undefined as the graph of f (x) = (x−23)
2 by checking the end behavior, behavior near
zeros, and behavior near points where g is undefined. Show that the vertical asymptote of
g is the line x = b.
Example. Find the end behavior, find the zeros, and find the points where the function is
undefined. Check the behavior of the function at the points where the function has a zero
or where the function is undefined, and sketch the graph. Include any vertical asymptote
of the function on the same set of coordinates.
f (x) =
341
.
(x − 23)3
Solution. End Behavior:
For x → ∞, f (x) ≈ 341
. For x → ∞,
x3
341
x3
is positive and
For x → −∞, that is, for -(large) x, f (x) ≈
341
→ 0− .
x3
341
.
x3
341
x3
→ 0+ .
For x → −∞,
341
x3
is negative and
Zeros:
f has no zeros.
Undefined:
f is undefined at x = 23.
Behavior near x = 23:
For x → 23− , f (x) < 0 and f (x) → −∞.
For x → 23+ , f (x) > 0 and f (x) → ∞.
Therefore, the vertical line x = 23 is a vertical asymptote of f .
A sketch of the graph of f is given below. The dashed line is not part of the graph of f ;
It is the vertical asymptote x = 23. It is customary to include the graph of the vertical
asymptote with the graph of the function for clarity.
2.3. GRAPHS OF RATIONAL FUNCTIONS
49
y
x
a
Exercise. Show that the graph of g(x) = (x−b)
n , where a is a positive constant, b is a
constant, and n is odd, has the same end behavior and same behavior near the point where
341
g is undefined as the graph of f (x) = (x−23)
by checking the end behavior, behavior near
zeros and behavior near points where g is undefined. Show that the vertical asymptote of
g is the line x = b.
Example. Find the end behavior, find the zeros, and find the points where the function is
undefined. Check the behavior of the function at the points where the function has a zero
or where the function is undefined, and sketch the graph. Include any vertical asymptote
of the function on the same set of coordinates.
f (x) =
−341
.
(x − 23)3
Solution. End Behavior:
. For x → ∞,
For x → ∞, f (x) ≈ −341
x3
−341
x3
is positive and
For x → −∞, that is, for -(large) x, f (x) ≈
−341
→ 0− .
x3
Zeros:
f has no zeros.
Undefined:
f is undefined at x = 23.
Behavior near x = 23:
For x → 23− , f (x) < 0 and f (x) → −∞.
−341
.
x3
−341
x3
→ 0+ .
For x → −∞,
−341
x3
is negative and
50
CHAPTER 2. GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
For x → 23+ , f (x) > 0 and f (x) → ∞.
Therefore, the vertical line x = 23 is a vertical asymptote of f .
A sketch of the graph of f is given below. The dashed line is not part of the graph of f ;
it is the vertical asymptote x = 23. It is customary to include the graph of the vertical
asymptote with the graph of the function for clarity.
y
x
a
Exercise. Show that the graph of g(x) = (x−b)
n , where a is a negative constant, b is a
constant and n is odd, has the same end behavior and the same behavior near the point
−341
where g is undefined as the graph of f (x) = (x−23)
by checking the end behavior, behavior
near zeros, and behavior near points where g is undefined. Show that the vertical asymptote
of g is the line x = b.
We can summarize our findings of basic rational functions in the following four graphs.
2.3. GRAPHS OF RATIONAL FUNCTIONS
51
y
y
x
x
a
(a) f (x) = (x−b)
n , where a > 0
and n is odd
a
(b) f (x) = (x−b)
n , where a < 0
and n is odd
Figure 3
y
y
x
x
a
(a) f (x) = (x−b)
n , where a > 0
and n is even
a
(b) f (x) = (x−b)
n , where a < 0
and n is even
Figure 4
Let us look at even more general rational functions now.
g(x)
Let f (x) = h(x)
be a rational function. The polynomial g(x) is called the “numerator” of
f and the polynomial h(x) is called the “denominator” of f .
We will separate the rational functions into two categories.
Category 1: The degree of the numerator is less than the degree of the denominator.
52
CHAPTER 2. GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
Category 2: The degree of the numerator is greater than or equal to the degree of the
denominator.
Let us look at Category 1 first. Let us assume that the given rational function can be
factored into linear and irreducible quadratic factors.
With the information in Figures 1, 2, 3, and 4, we can sketch the graphs of such Category
1 functions.
Example. Find the end behavior, find the zeros, and find the points where the function is
undefined. Check the behavior of the function at the points where the function has a zero
or where the function is undefined and, sketch the graph. Include any vertical asymptote
of the function on the same set of coordinates.
f (x) =
31(x − 45)(x + 34)2
.
(x − 23)3 (x2 + 1)
Solution. End Behavior:
3
For x → ∞, f (x) ≈ 31x
= x312 . Therefore, the end behavior of f (x) is the same as the
x5
a
end behavior of f (x) = (x−b)
2 , where a > 0, b = 0.
x
Zeros:
The zeros of f are 45 and −34.
Behavior near x = 45:
Near x = 45, f (x) ≈ k1 (x − 45), where k1 is a positive constant. Therefore, the behavior
of f near x = 45 is like the graph of a line with a positive slope.
(45, 0)
x
2.3. GRAPHS OF RATIONAL FUNCTIONS
53
Behavior near x = −34:
Near x = −34, f (x) ≈ k2 (x+34)2 , where k2 is a positive constant. Therefore, the behavior
of the graph of f near x = −34 is like the graph of g1 (x) = k2 (x + 34)2 near x = 34.
(−34, 0)
x
Undefined:
f is undefined at x = 23.
Behavior near x = 23:
k3
Near x = 23, f (x) ≈ (x−23)
3 , where k3 is a negative constant. Therefore, the behavior of
k3
the graph f near x = 23 is like the behavior of g(x) = (x−23)
3 , k3 < 0.
The vertical line x = 23 is a vertical asymptote of f .
We can sketch of the graph of f with the collected information and sticking to our motto.
A sketch of the graph including the vertical asymptote is given below.
2.3. GRAPHS OF RATIONAL FUNCTIONS
Let us look at Category 2 rational functions now. That is, f (x) =
of g(x) is greater than or equal to the degree of h(x).
55
g(x)
,
h(x)
where the degree
Euclidean Algorithm Theorem. Given polynomials g(x) and h(x), there are
unique polynomials q(x) and r(x) so that
g(x) = q(x)h(x) + r(x), where, the degree of r(x) < the degree of h(x).
The following theorem is the same Euclidean Algorithm Theorem when h(x) 6= 0.
Euclidean Algorithm Theorem – version 2. Given polynomials g(x) and h(x),
there are unique polynomials q(x) and r(x) so that
r(x)
g(x)
= q(x) +
, where the degree of r(x) < the degree of h(x).
h(x)
h(x)
We will omit the proof of this theorem. You may have learned the Long Division Algorithm
for polynomials in high school. Given g(x) and h(x), you can use the Long Division
Algorithm to find q(x) and r(x). The following example demonstrates the process.
Example. If g(x) = x3 − 2x2 + 4x + 5 and h(x) = x2 − 3, then find q(x) and r(x) that
satisfy the Euclidean Algorithm Theorem – version 2.
x−1
x2 − 3 x3 − x2 + 4x + 5
−3x
x3
−x2 + 7x + 5
−3
−x2
−
−
7x + 2
Therefore,
x3 − x2 + 4x + 5
7x + 2
=x−1+ 2
.
2
x −3
x −3
56
CHAPTER 2. GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
We will first look at the special case of degree of p(x) = degree of q(x).
Example. Find the end behavior of f (x) =
3x+4
.
x−1
Solution. By using the Long Division Algorithm, we can write f as:
f (x) = 3 +
7
.
x−1
7
Now for x → ∞, x−1
→ 0+ and
7
→ 0− . In either case, f (x) ≈ 3.
for x → −∞, x−1
Given a function f (x), if there is a function q(x) so that f (x) − q(x) ≈ 0 for x → ±∞,
then we say y = q(x) is a non-vertical asymptote of f .
In the given example, y = 3 is a non-vertical asymptote of f . Since we know that the
graph of y = 3 is a horizontal line, we usually say y = 3 is a horizontal asymptote of
f (x) = 3x+4
.
x−1
Theorem. Suppose the degree of r(x) is less than the degree of h(x). Then for x →
r(x)
±∞, h(x)
≈ 0.
Exercise. Prove the previous theorem.
Theorem. Let f (x) =
g(x)
.
h(x)
Then the non-vertical asymptote of f is y = q(x), where
r(x)
g(x)
= q(x) +
, and the degree of r(x) < the degree of h(x).
h(x)
h(x)
Proof. The proof of this theorem follows directly from the Euclidean algorithm and the
previous theorem.
The word corollary stands for a “little” theorem. Usually the word “corollary” is a little
theorem associated with an existing theorem. We use the word corollary for a theorem if
it “falls out of” an existing theorem.
The following is a corollary to the previous theorem.
2.3. GRAPHS OF RATIONAL FUNCTIONS
57
Corollary.
1. If f (x) is a rational function of Category 1 (that is, the degree of the denominator
> the degree of the numerator), then the non-vertical asymptote is a horizontal
asymptote, and it is y = 0.
2. If f (x) is a rational function of Category 2 (that is, the degree of the denominator
≤ the degree of the numerator), then the non-vertical asymptote is y = q(x).
Exercise. Prove the previous corollary.
Suppose the function f is not defined at x = a. Suppose also that there is a real number
L so that for x → a− , f (x) ≈ L and for x → a+ , f (x) ≈ L. Then we say that f has a
hole at x = a.
y
This function has a hole at a
L
a
x
The following example demonstrates the method of sketching graphs of rational functions
of Category 2.
Example. For the given function, find the end behavior, find the zeros, find the asymptotes, find the holes, find the behavior near each zero, find the behavior near each asymptote
58
CHAPTER 2. GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
, and sketch the graph accurately.
f (x) =
2x3 + 3x2 − 2x
x2 − 4
Solution. Since the degree of the numerator is less than the degree of the denominator,
(Category 2), we can use the Long Division Algorithm to write this function as
f (x) = 2x + 3 +
6x − 12
x2 − 4
Therefore, y = 2x + 3 is a non-vertical asymptote. This type of a linear asymptote is also
known as a slant asymptote.
≈ 6x
= x6 . Therefore,
End behavior: For x → ∞, 6x−12
x2 −4
x2
For x → ∞, f (x) ≈ 2x + 3 +“ a very small positive number”.
≈ 6x
= x6 . Therefore,
For x → −∞, 6x−12
x2 −4
x2
For x → −∞, f (x) ≈ 2x + 3 +“ a very small negative number”.
Now we will factor f completely.
f (x) =
x(2x − 1)(x + 2)
.
(x − 2)(x + 2)
The factor (x + 2) is common to both numerator and the denominator of f (x).1 Clearly,
f is not defined at x = −2. Also, for all real numbers x 6= −2, f (x) and
g(x) =
x(2x − 1)
(x − 2)
are identical. This is because,
(x+2)
(x+2)
= 1, for x 6= −2.
Near −2 (That is, for x → −2− and for x → −2+ ):
= − 23 .
f (x) ≈ (−2)(2(−2)+1)
(−2−2)
Therefore, f has a hole at x = −2.
Now we will concentrate on g as f (x) = g(x) for all x 6= −2.
Zeros of g (these are also the zeros of f ):
The zeros of g are 0 and 21 .
10
0
is so called an indeterminate form. You may learn about indeterminate forms in a calculus class.
If we agree that a division by zero is invalid, no matter what, then we do not have to be concerned about
indeterminate forms here.
2.3. GRAPHS OF RATIONAL FUNCTIONS
59
Near 0:
Near 0, g(x) ≈ 12 x. Therefore, near 0, the graph of g (and hence the graph of f ) looks
like a line with a positive slope.
Near 21 :
Near 21 , g(x) ≈ − 13 (2x + 1). Therefore, near 21 , the graph of g (and hence the graph of f )
looks like a line with a negative slope.
g is undefined at x = 2:
6
. Therefore, the graph of g looks like the graph of g1 (x) =
Near x = 2, g(x) ≈ x−2
near x = 2. The vertical asymptote of g is x = 2.
By using all the collected information, we can sketch the graph of f now.
y
y = 2x + 3
x=2
1
2
Hole at x = −2
x
6
x−2
Chapter 3
Sequences, Series, Mathematical
Induction
3.1
Sequences and Series
We will introduce new notation to represent real numbers, rational numbers, integers and
natural numbers. (The natural numbers are the positive integers. The natural numbers
are also known as counting numbers.) We will use R to represent all real numbers; we
will use Q to represent all rational numbers; we will use Z to represent all integers; and
we will use N to represent all natural numbers. If we want to talk about all except a
few real numbers, say “all real numbers except 1 and 2”, then we will use the notation
R \ {1, 2}.
You have seen polynomial functions and rational functions so far. The domain of a polynomial function is R. The domain of a rational function is R\{points where the denominator is zero}.
Now we will look at a special class of real-valued functions whose domain is N. The
natural numbers differ from real numbers in many ways. In particular, there is a first
natural number, namely, 1. However, there is no first real number. For every natural
number, there is a next natural number. For example, the natural number next to 1
is 2. Because of this special nature of natural numbers, there is a first element for a
function f with domain N; namely, f (1). The next element to f (1) is f (2). Just like we
can list the natural numbers as {1, 2, 3, . . . , k, k + 1, . . .}, we can list the elements of f as
{f (1), f (2), f (3), . . . , f (k), f (k + 1), . . .}, where k is an arbitrary natural number.
Because of this property, we usually call a real-valued function with domain N a sequence.
61
62
CHAPTER 3. SEQUENCES, SERIES, MATHEMATICAL INDUCTION
The first element of the sequence is f (1), the second element of the sequence is f (2), etc.
and the kth element of the sequence is f (k)., for some arbitrary natural number k.
Another convention is to drop the functional notation when dealing with sequences and
just indicate the position of an element using a subscript. Therefore, f (1) is usually
written as f1 , and f (2) is usually written as f2 , etc. But, then you should realize that
this new notation conflicts with our previous use of f1 , f2 to represent different functions.
For this reason, we will replace the letter f with the letter a when we are dealing with
sequences.
A given sequence can be represented as {a1 , a2 , a3 , . . . , an , . . . , }, where a1 is the first
element of the sequence, a2 is the second element of the sequence, a3 is the third element
of the sequence, and an is the nth element of the sequence, for an arbitrary natural number
n.
Since sequences are functions, everything we know about functions can be used.
Example. Consider f (x) = x2 − 2x − 3, one of the familiar quadratic functions. Since
we know what the function is, we can find the function value at any given value of x. For
example, f ( 21 ) = ( 12 )2 − 2( 12 ) − 3, by the definition of the functional notation that you may
have learned in high school.
Now suppose an = n2 − 2n − 3 is the nth term of a sequence. Then we can find a5 as
follows. a5 = 52 − 2(5) − 3.
As matter of fact, if an is given, then we can find any element of the sequence, just like
given f (x), we can find any function value of f .
For this reason, an is called the general term of a sequence. There is no special reason
why we should use n as a subscript of the general term. Any lower case letter other than
a is fine to use as the subscript of the general term of a sequence. But, most of the time,
unless there is a very specific reason not to use n, we will use an to represent the general
term of a sequence.
Example. Consider f (x) = 31 , one of the constant functions. For example, if we want to
find what f (5) is, then it should be clear that f (5) = 31 ,
Now suppose an = 31 is the nth term of a sequence. Then, if we want to find the fifth term
of this sequence. a5 = 31 , by the definition of the functional notation.
3.1. SEQUENCES AND SERIES
63
It is clear that if we know the general term of a sequence, then we can get any term of
the sequence. Because of that, we express sequences just using the nth term as in the
following notation.
{an }∞
n=1
This notation means, “the set of all an , where n varies over natural numbers”. That is,
{an }∞
n=1 = {a1 , a2 , a2 , . . . , an , . . . }
Exercise. Identify the first five terms of the given sequence.
n
1. { n+1
}∞
n=1
2
k
2. { k+2
}∞
k=1
n! ∞
3. { n+3
}n=1
Here, n! stands for the number n(n−1)(n−2) · · · 3·2·1. For example, 5! = 5·4·3·2·1.
Consider a sequence {an }∞
n=1 . The sum of the first n terms of the sequence is called the
nth partial sum of the sequence. We will usually use Sn to represent the nth partial sum
of a sequence. That is,
Sn = a1 + a2 + a3 + · · · + an−2 + an−1 + an .
If we can add all elements of a sequence, then we call it a series. For example,
a1 + a2 + a3 + · · · + an−2 + an−1 + an + · · ·
is a series. However, this notation is not that great as the last three dots (· · · ), which
usually stand for “and so on” now stand for “and so on without bounds”. We can use the
following superior notation to represent a series.
∞
X
an
n=1
This notation stands for “the sum of all an , where n varies over natural numbers”.
This notation also gives us another way to represent the nth partial sum of a sequence.
n
X
ak
k=1
The above notation stands for “the sum of all ak , where k varies over natural numbers
from 1 to n”. The nth partial sum of a sequence is occasionally known as a finite series.
64
CHAPTER 3. SEQUENCES, SERIES, MATHEMATICAL INDUCTION
Exercise. Identify the first five terms of the sequence
n
1. Find the 5th partial sum of the sequence { n+1
}∞
n=1 .
2
k
2. Find the 5th partial sum of the sequence. { k+2
}∞
k=1 .
n! ∞
3. Find the 5th partial sum of the sequence. { n+3
}n=1 .
4. Find
5
P
k=1
3.1.1
k+1
.
k+2
Arithmetic Sequences and Series
Consider the following sequence.
1
1 + (n − 1)
2
∞
n=1
The first seven terms of this sequence are {1, 32 , 2, 25 , 3, 72 , 4, . . . }.
7
6
5
4
3
2
1
a7
a6
a5
a4
a3
a2
a1
1
2
3
4
5
6
7
Notice that the difference between any two consecutive terms of the sequence is 12 .
3.1. SEQUENCES AND SERIES
a1 =
1 + 12 (1 − 1) =
1
a2 =
1 + 21 (2 − 1) =
3
2
a3 =
1 + 12 (3 − 1) =
2 =
a4 =
1 + 12 (4 − 1) =
5
2
a5 =
1 + 12 (5 − 1) =
3 =
a6 =
1 + 12 (6 − 1) =
7
2
a7 =
..
.
1 + 12 (7 − 1) =
4 =
ak =
1 + 21 (k − 1)
ak+1 =
1 + 12 ((k + 1) − 1) =
65
=1+
1
2
3
2
+
1
2
=2+
1
2
5
2
+
1
2
=3+
1
2
7
2
1
2
+
1 + 12 k = ak + 12 ,
where k is an arbitrary positive integer.
A sequence with this property, that is, the difference between any two consecutive terms is
a constant, is called an arithmetic sequence. The difference between any two consecutive
terms of an arithmetic sequence is called the common difference.
Theorem. Let a be the first term of an arithmetic sequence and let d be the common
difference. Then the general term of the sequence is an = a + (n − 1)d.
Exercise. Prove the previous theorem.
If we denote a as the first term of an arithmetic sequence1 and d as the common difference,
then we can denote every element of the arithmetic sequence in terms of a and d as shown
below:
{a, (a + d), (a + 2d), (a + 3d), . . . , (a + (n − 1)d), . . .}
Example. Show that {15 − 34 n}∞
n=1 is an arithmetic sequence.
1
It is a convention to write a1 as just a for arithmetic sequences and soon to be introduced geometric
sequences.
66
CHAPTER 3. SEQUENCES, SERIES, MATHEMATICAL INDUCTION
Solution. By definition, if the difference between any two consecutive terms is a constant,
then the sequence is an arithmetic sequence. Therefore, our goal is to show that the
difference between any two consecutive terms of the given sequence is a constant.
On the face of it, this is an impossible task. There are infinitely many natural numbers and
therefore, there are infinitely many pairs of consecutive terms to check. The mathematical
solution to this conundrum is the following. We will show that the difference between ak+1
and ak is a constant, for an arbitrary natural number k. If we can do that, then since k
is arbitrary, we have shown that the difference between any two consecutive terms of the
sequence is a constant. This is a standard mathematical technique when you are left to
check infinitely many cases.
Let k be an arbitrary natural number. Then ak = 15 − 34 k and ak+1 = 15 − 43 (k + 1).
Therefore,
4
4
ak+1 − ak = 15 − (k + 1) − 15 − k
3
3
4
4
4
= 15 − k − − 15 + k
3
3
3
4
=−
3
Since k is arbitrary, the difference between any two consecutive terms of the given sequence
is the constant − 43 . Therefore, the given sequence is an arithmetic sequence.
Let Sn be the nth partial sum of an arithmetic sequence with the first term a and the
common difference d. Then
Sn = a+(a+d)+(a+2d)+(a+3d)+· · ·+(a+(n−3)d)+(a+(n−2)d)+(a+(n−1)d).
For the following argument, let us look at the first term a1 , that is a, as a + 0d. In other
words, the first term is a sum of “an a” and “no d” terms. The nth term is a + (n − 1)d.
That is, the nth term is a sum of “an a” and “(n − 1) number of d terms”. If we add the
first term and the last term together, that is, a1 + an , then we get 2a + (n − 1)d. Now
look at a2 + an−1 : a2 has one more d than a1 , and an−1 has one less d that an . Therefore,
a2 + an−1 has the same number of d terms as a1 + an . Therefore, a2 + an−1 = 2a + (n − 1)d
as well. If we look at a3 + an−2 , then a3 has two more d terms than a1 , and an−2 has two
less d terms that an . Therefore, a3 + an−2 has the same number of d terms as a1 + an .
Therefore, a3 + an−2 is also equal to 2a + (n − 1)d. This kind of thinking leads us to the
next theorem.
3.1. SEQUENCES AND SERIES
67
Theorem. If {an }∞
n=1 is an arithmetic sequence with a1 = a and the common difference d, then the nth partial sum, Sn , is given by the following formula.
Sn =
n
[2a + (n − 1)d]
2
Proof. Case 1: Suppose n is even. Then n2 is a natural number, since n is divisible by 2.
There are two middle terms and the middle two terms are an/2 and an/2+1 .
Sn = a1 + a2 + a3 + · · · + an/2 + an/2+1 + · · · + an−2 + an−1 + an .
This sum can be written as:
Sn = (a1 + an ) + (a2 + an−1 ) + (a3 + an−2 ) + · · · + (an/2 + an/2+1 ).
Which is the same as:
Sn = [2a + (n − 1)d] + [2a + (n − 1)d] + [2a + (n − 1)d] + · · · + [2a + (n − 1)d].
The term [2a + (n − 1)d] in Sn repeats
Sn =
n
2
in S − n. Therefore,
n
[2a + (n − 1)d].
2
is a natural number since n+1 is
Case 2: Now suppose n is odd. Then n+1 is even and n+1
2
divisible by 2. In this case, there is only one middle term, and the middle term is a(n+1)/2 .
According to the general term of an arithmetic sequence, a(n+1)/2 = a + ((n + 1)/2 − 1)d.
Sn = a1 + a2 + a3 + · · · + a(n−1)/2 + a(n+1)/2 + a(n+3)/2 + · · · + an−2 + an−1 + an .
This sum can be written as:
Sn = (a1 + an ) + (a2 + an−1 ) + (a3 + an−2 ) + · · · + (a(n−1)/2 + a(n+3)/2 ) + a(n+1)/2 .
Which is the same as:
Sn =
n−1
[2a + (n − 1)d] + a(n+1)/2 .
2
By identifying the a(n+1)/2 term we get:
n−1
n+1
Sn =
[2a + (n − 1)d] + a +
−1 d .
2
2
68
CHAPTER 3. SEQUENCES, SERIES, MATHEMATICAL INDUCTION
Which is the same as:
n−1
n−1
Sn =
[2a + (n − 1)d] + a +
d .
2
2
That is,
Sn =
n−1
1
[2a + (n − 1)d] + [2a + (n − 1)d].
2
2
By factoring out the common term, we get:
n−1 1
Sn =
+
[2a + (n − 1)d].
2
2
Which is the same as:
Sn =
n
[2a + (n − 1)d].
2
Example. Find
100
P
2n, if possible.
n=1
Solution. We can restate this problem as follows. Find the 100th partial sum of the
∞
sequence {2n}∞
n=1 . If the sequence {2n}n=1 is arithmetic, then we can use the previous
theorem to answer the given question. Therefore, our first order of business is to check
and see if the sequence is arithmetic. For an arbitrary natural number k,
ak+1 − ak = 2(k + 1) − 2k
= 2k + 2 − 2k
=2
Since k is arbitrary, the difference between any two consecutive terms of the sequence
∞
{2n}∞
n=1 is 2. Therefore, {2n}n=1 is arithmetic, with the first term 2 and the common
difference 2. Then
100
[2(2) + (100 − 1)(2)]
2
= 50[4 + (99)(2)]
S100 =
= 10, 100.
3.1. SEQUENCES AND SERIES
3.1.2
69
Geometric Sequences and Series
The following definition and the theorem that you may have learned in high school are
extremely useful in this section.
Definition. Let a 6= 0 be a real number and n be a positive integer. Then
1. a0 = 1.
2. a1 = a
3. a−n =
1
an
Integer Powers Theorem. 2 Suppose a 6= 0 and b 6= 0 are real numbers and m and
n are integers. Then
1. an am = an+m
2. (an )m = anm
3.
an
am
= an−m
4. (ab)n = an bn
5.
a n
b
=
an
bn
Consider the following sequence.
( )∞
n−1
1
3
2
n=1
The first five terms of this sequence are {3, 32 , 232 , 233 , 234 . . . }.
2
You may have proved this theorem for rational powers in high school.
70
CHAPTER 3. SEQUENCES, SERIES, MATHEMATICAL INDUCTION
3
a1
2
a2
1
a5
a3
a4
1
2
3
4
5
6
7
Notice that the ratio between any two consecutive terms of the sequence is 21 .
a1 =
3
1 1−1
2
=
3
a2 =
3
1 2−1
2
=
3
2
a3 =
3
1 3−1
2
=
3
22
= a2
1
2
a4 =
3
1 4−1
2
=
3
23
= a3
1
2
a5 =
..
.
3
1 5−1
2
=
3
24
= a4
1
2
=
3
2k
= ak
ak =
3
1 k−1
2
ak+1 =
3
1 k+1−1
2
= a1
1
2
1
2
where k is an arbitrary positive integer.
A sequence with this property, that is, the ratio between any two consecutive terms is a
constant, is called an geometric sequence. The ratio between any two consecutive terms
of a geometric sequence is called the common ratiocommon ratio—textbf.
Theorem. Let the first term of a geometric sequence be a and let the common ratio
be r. Then the general term of the sequence is an = arn−1 .
Exercise. Prove the previous theorem.
Let a denote the first term of a geometric sequence and let r denote the common ratio.
Then we can denote every element of the geometric sequence in terms of a and r as shown
3.1. SEQUENCES AND SERIES
71
below:
{a, ar, ar2 , ar3 , . . . , arn−1 , . . .}
Example. Show that {15
4 n ∞
}n=1
3
is a geometric sequence.
Solution. By definition, if the ratio between any two consecutive terms is a constant, then
the sequence is a geometric sequence. Therefore, our goal is to show the ratio between any
two consecutive terms of the given sequence is a constant.
Let k be an arbitrary natural number. Then
k+1
15 34
ak+1
=
k
ak
15 4
3
=
15
15
=
4 k 4
3
3
4 k
3
4
3
Since k is arbitrary, the ratio between any two consecutive terms of the given sequence is
the constant 43 . Therefore, the given sequence is a geometric sequence.
Finite Geometric Series Theorem. Given a geometric sequence {arn−1 }∞
n=1 , where
th
a is the first term and r is the common ratio, then the n partial sum of {arn−1 }∞
n=1
is
Sn =
a(1 − rn )
.
1−r
Proof. Let Sn be the nth partial sum of a geometric sequence with the first term a and
the common ratio r. Then
Sn = a + ar + ar2 + ar3 + · · · + arn−3 + arn−2 + arn−1 .
Notice that
rSn = ar + ar2 + ar3 + ar4 · · · + arn−2 + arn−1 + arn .
72
CHAPTER 3. SEQUENCES, SERIES, MATHEMATICAL INDUCTION
That is,
rSn − arn = ar + ar2 + ar3 + ar4 · · · + arn−2 + arn−1 .
That is,
rSn − arn = −a + a + ar + ar2 + ar3 + ar4 · · · + arn−2 + arn−1 .
That is,
rSn − arn = −a + Sn .
Now, this is a linear equation in Sn . By solving this linear equation for Sn , we get:
Sn =
a(1 − rn )
.
1−r
Example. Find
20
P
n=1
1 n
,
2
if possible.
Solution. For an arbitrary natural number k,
1 k+1
ak+1
2
=
1 k
ak
2
k+1−k
1
=
2
=
1
2
n
Since k is arbitrary, the ratio between any two consecutive terms of the sequence { 21 }∞
n=1
1
1 n ∞
1
1
is 2 . Therefore, { 2 }n=1 is geometric, with the first term 2 and the common ratio 2 . If
n−1 ∞
}n=1 .
we write the general term in the form arn−1 , then the geometric sequence is { 12 21
Now we can calculate S20 by using the Finite Geometric Series Theorem.
S20 =
=
1
2
1 20
2
1−
1−
1
2
1−
1
2
1
2
1
220
3.1. SEQUENCES AND SERIES
=1−
1
220
=1−
1
1048576
=
1048576 − 1
1048576
=
1048575
1048576
73
In the previous example, S20 , is very close to 1, but less than 1. Would the nth partial
sum be more than 1 for some high natural number n? We can do a calculator experiment,
within the limitations of TI-83 calculator. (The largest exact value for 2n that can be
obtained in a TI-83 calculator is when n = 33.)
Example. Find
33
P
n=1
1 n
,
2
if possible.
Solution.
1 33
1
1
−
2
2
S33 =
1 − 21
=
1
2
1−
1
233
1
2
=1−
1
233
=1−
1
8589934592
=
8589934592 − 1
8589934592
=
8589934591
8589934592
The 33rd partial sum is even closer to 1 but still less than 1. Since we have reached the
limits of calculators, we need to look for a purely mathematical way of moving forward.
n
If we can show that, 12 → 0, for n → ∞, then it follows that, for larger values of n,
Sn ≈ 1, by the Finite Geometric Series Sum Theorem.
74
CHAPTER 3. SEQUENCES, SERIES, MATHEMATICAL INDUCTION
The following theorem is beyond the scope of Precalculus. (This is the second such
theorem that we have encountered so far.) However, it is not hard to imagine its truth.
The Archimedean Property Theorem. Suppose R is a positive real number. Then
there is a natural number N so that N > R.
That is, no matter how big the real number R is, we can always find a natural number
bigger than R.
The following theorem is also needed; however, we cannot prove it yet. We will prove
this theorem when we learn the method, “Proof by Mathematical Induction”, in the next
lesson.
Theorem (Theorem 5). Suppose n is any natural number. Then 2n > n.
Theorem. Suppose r = 12 . Then, for n → ∞, rn → 0.
Notation: We will use =⇒ to replace the English word “implies”.
Proof. Let r = 12 . Clearly, r < 1. We will use Theorem 3 repeatedly.
r < 1 =⇒ r2 < r.
r2 < r =⇒ r3 < r2 .
r3 < r2 =⇒ r4 < r3 .
..
.
rk < rk−1 =⇒ rk+1 < rk .
..
.
3.1. SEQUENCES AND SERIES
75
That is, if 0 < r < 1, then 0 < · · · rk+1 < rk < · · · < r4 < r3 < r2 < r < 1, where, k is a
sufficiently large arbitrary natural number. (In this case, k > 4 by choice.)
That is, as “n increases” the value of “rn decreases” while remaining positive. Could
rn be always bigger than some small, but positive number , for any n? If so, then for
n → ∞, rn → . Our gut feeling is that this is not the case. But how can we be sure it is
not the case? One mathematical method that we can use is to assume a given statement
is true and then look for a contradiction that will show that the assumption is false. This
type of proof is known as “proof by contradiction”. (We have used this method when
solving equations without mentioning the name “proof by contradiction”.)
Suppose that there is a positive number so that < rn < 1, for all natural numbers n.
Then 1e > 1. By Archimedean Property Theorem, there is a natural number N so that
N > 1 . By Theorem 5, 2N > N . That is, 2N > N > 1 . Then 21N < N1 < . That is,
1 N
< N1 < . That is, rN < N1 < . This contradicts our assumption that rn > , for
2
all natural numbers n. Therefore, our assumption is false, and rn → 0 for n → ∞.
The following general theorem is also true. But the proof is hard (as you may have guessed
from the special case of this theorem that we just proved).
Theorem (Theorem 6). Suppose |r| < 1. Then, for n → ∞, rn → 0.
We will use the symbol S∞ to represent
∞
P
∞
P
an . That is, S∞ stands for the infinite series
n=1
an .
n=1
Infinite Geometric Series Theorem. Consider the geometric sequence {arn−1 }∞
n=1 ,
a
where a is the first term and r is the common ratio. Suppose |r| < 1. Then S∞ = 1−r
.
Proof. The proof of this theorem follows from the Finite Geometric Series Theorem and
Theorem 6.
n
Example. Find S∞ for the sequence { 89 }, if possible.
76
CHAPTER 3. SEQUENCES, SERIES, MATHEMATICAL INDUCTION
Solution. For an arbitrary natural number k,
8 k+1
9
8 k
9
ak+1
=
ak
k+1−k
8
=
9
=
8
9
n
Since k is arbitrary, the ratio between any two consecutive terms of the sequence { 98 }∞
n=1
8
8 n ∞
8
8
is 9 . Therefore, { 9 }n=1 is geometric, with the first term 9 and the common ratio 9 .
Clearly, | 89 | < 1. Therefore, by the Infinite Geometric Series Theorem,
8
9 S∞ =
1 − 89
8
9
1
9
=
=8
3.2
Mathematical Induction
This is a very important method of proving theorems with the following characteristics.
1. The theorem contains infinitely many countable statements to prove.
2. There is a first statement.
3. For any statement, there is a next statement.
Clearly, the proof by mathematical induction is intimately related to the natural numbers;
as there are infinitely many (countable) natural numbers; there is a first natural number;
and for any natural number, there is a next natural number. The proof by mathematical
induction is a two-step process. The first step, known as the “first step” (no surprise
here!) is to prove the first statement. The second step, known as the “inductive step” is
to assume that the k th statement is true, for some natural number k, and then prove that
the statement next to the k th statement is also true. If you are successful in completing
3.2. MATHEMATICAL INDUCTION
77
the first step and the inductive step, then we say that, by mathematical induction, all
statements must be true.
The argument goes as follows. We have shown that the first statement is true. Then by
the inductive step, the next statement, that is, the second statement is also true. Since
the second statement is true, then by the inductive step, the statement following the
second statement, that is, the third statement, is also true. By continuing in this process,
it should be clear that you can prove the nth statement, for any natural number n.
Example. Prove that 2n > n, for all natural numbers n, by using mathematical induction.
Proof. First notice that there are infinitely many countable statements to prove in the
exercise. Namely:
1. Show that 21 > 1.
2. Show that 22 > 2.
3. Show that 23 > 3.
..
.
and ad infinitum. (That is, again and again in the same way, forever.)
Clearly, this is an impossible task — if you insist on proving each statement. But, fortunately, this theorem satisfies the three requirements that we need to use the proof by
mathematical induction. That is, (1) there are infinitely many statements; (2) there is a
first statement; and (3) for each statement there is a next statement. Therefore, we will
use mathematical induction to prove this theorem.
First step: Show that the first statement of the theorem is true. That is, show that
21 > 1 is true.
Clearly, 2 > 1. Therefore, the first statement of the theorem is true.
Inductive step: Assume that the k th statement of the theorem is true, for some arbitrary
natural number k. That is, assume:
2k > k is true.
—— (A)
and then show that
2k+1 > k + 1 is also true.
—– (B)
78
CHAPTER 3. SEQUENCES, SERIES, MATHEMATICAL INDUCTION
Let us attend to the task at hand now.
The left side of (B) = 2k+1
= 2(2k )
> 2k, by (A).
=k+k
≥ k + 1 because, k ≥ 1.
That is, 2k+1 > k + 1 is true.
Thus, we showed that, if the k th statement of the theorem is true, for some arbitrary
natural number k, then the k + 1st statement of the theorem is also true.
Therefore, by mathematical induction, the theorem must be true for any natural number
n.
Example. Prove that x − 1 is a factor of xn − 1 for all natural numbers n, by using
mathematical induction.
Proof. Clearly, there are infinitely many countable statements to prove; there is a first
statement; and for each statement, there is a next statement. Therefore, we can use
mathematical induction to prove this theorem.
First step: Show that the first statement of the theorem is true. That is, show that
x − 1 is a factor of x1 − 1. This statement is clearly true, since (1)(x − 1) = x − 1.
Inductive step: Assume that the k th statement of the theorem is true, for some arbitrary
natural number k. That is, assume that:
x − 1 is a factor of xk − 1 is true.
—— (A)
and show that
x − 1 is a factor of xk+1 − 1 is also true.
—— (B)
Now, let us prove (B). First, notice that there is a polynomial p(x) so that xk − 1 =
(x − 1)p(x), by (A).
xk+1 − 1 = xk+1 − x + x − 1
= x(xk − 1) + (x − 1)
3.2. MATHEMATICAL INDUCTION
79
= x(x − 1)p(x) + (x − 1)
= (x − 1)[xp(x) + 1]
That is, if (x − 1) is a factor of xk − 1, then (x − 1) is a factor of xk+1 − 1.
Therefore, by mathematical induction, the theorem is true for any natural number n.
Example. Prove that
1
1
1
n
1
+
+
+ ··· +
=
1·2 2·3 3·4
n(n + 1)
n+1
for all natural numbers n, by using mathematical induction.
Proof. Notice first that the left side of the given equation is the nth partial sum of the
1
1
th
sequence { n(n+1)
partial sum of the sequence { n(n+1)
}∞
}∞
n=1 . Let Sn be the n
n=1 , for any
n
natural number n. Then, the task of the theorem is to show that Sn = n+1 , for all natural
numbers n.
First step: Show that the first statement of the theorem is true. That is, show that
1
S1 = 1+1
true.
S1 =
1
1
= .
1·2
2
1
1
= .
1+1
2
Therefore, S1 =
1
1+1
true. That is, the first statement is true.
Inductive step: Assume that the k th statement of the theorem is true, for some arbitrary
natural number k. That is, assume
Sk =
k
is true,
k+1
That is, assume
1
1
1
1
k
+
+
+ ··· +
=
is true,
1·2 2·3 3·4
k(k + 1)
k+1
and show that
Sk+1 =
k+1
is also true,
(k + 1) + 1
—— (A)
80
CHAPTER 3. SEQUENCES, SERIES, MATHEMATICAL INDUCTION
which is to say, show that
1
1
1
1
k+1
+
+
+ ··· +
=
is also true,
1·2 2·3 3·4
(k + 1)(k + 2)
k+2
—— (B)
Now, let us prove (B).
1
1
1
1
1
+
+
+ ··· +
+
1·2 2·3 3·4
k(k + 1) (k + 1)(k + 2)
1
= Sk +
(k + 1)(k + 2)
k
1
=
+
, by (A).
k + 1 (k + 1)(k + 2)
k(k + 2)
1
=
+
(k + 1)(k + 2) (k + 1)(k + 2)
k 2 + 2k + 1
=
(k + 1)(k + 2)
(k + 1)2
=
, by the Three Identities Theorem.
(k + 1)(k + 2)
k+1
, since k + 1 6= 0.
=
k+2
= The right side of (B)
The left side of (B) =
Therefore, if the k th statement is true, for some arbitrary natural number k, then the
k + 1st statement is also true.
Therefore, by mathematical induction, the theorem is true for any natural number n.
Exercise. Let Sn be the nth partial sum of the sequence {n}∞
n=1 . Show that
1
S1 + S2 + S3 + · · · + Sn = n(n + 1)(n + 2),
6
for any natural number n.
Chapter 4
Partial Fraction Decomposition
4.1
Solving Systems of Linear Equations (Review)
You may have learned how to solve systems of linear equations in high school. This section
is meant as a review.
Example. Find the solution of the system
3A + 4B − C
= 5
−4A + 7C
= −4
A − 2B + 4C
= 1,
(I)
where A, B, and C are real numbers.
Solution. We will assume that all three equations are true for some real numbers A, B,
and C. Then by the Four Properties Theorem, the following statements are true.
(i) If we multiply one equation by a non-zero number, then the new system of equations
is still true.
(ii) If we add one equation to another equation, then the new system of equations is still
true.
We will perform a series of actions of types (i) and (ii), until we get a system of three
81
82
CHAPTER 4. PARTIAL FRACTION DECOMPOSITION
equations
A
= a
(II)
B = b
C
= c
which are all true by design, if our original assumption is true. At this point we will check
and see if the solutions actually satisfy the original system of equations. If so, then, the
triple (a, b, c) is called the solution of the system.
The following is one way to get from system (I) to system (II).
Multiply the third equation of the system (I) by 4.
3A + 4B − C
= 5
−4A + 7C
= −4
4A − 8B + 16C
= 4
(4.1)
Add the second equation in the system (1) to the third equation in the system (1).
3A + 4B − C
= 5
−4A + 7C
= −4
−8B + 23C
= 0
(4.2)
Multiply the first equation of the system (2) by 4, and multiply the second equation of the
system (2) by 3.
12A + 16B − 4C
= 20
−12A + 21C
= −12
−8B + 23C
= 0
(4.3)
4.1. SOLVING SYSTEMS OF LINEAR EQUATIONS (REVIEW)
83
Add the first equation in the system (3) to the second equation in the system (3).
12A + 16B − 4C
= 20
16B + 17C
= 8
−8B + 23C
= 0
(4.4)
Multiply the third equation in the system (4) by 2.
12A + 16B − 4C
= 20
16B + 17C
= 8
−16B + 46C
= 0
(4.5)
Add the second equation in the system (5) to the third equation in the system (5).
12A + 16B − 4C
= 20
16B + 17C
= 8
63C
= 8
(4.6)
Multiply the second equation of the system (6) by 63, and multiply the third equation of
the system (6) by −17.
12A + 16B − 4C
= 20
1008B + 1071C
= 504
−1071C
= −136
(4.7)
Add the third equation in the system (7) to the second equation in the system (7).
12A + 16B − 4C
= 20
1008B
= 368
−1071C
= −136
(4.8)
84
CHAPTER 4. PARTIAL FRACTION DECOMPOSITION
1
Multiply the second equation in the system (8) by 1008
, and multiply the third equation in
1
the system (8) by − 1071 , and reduce the fractions.
12A + 16B − 4C
= 20
B
=
23
63
C
=
8
63
(4.9)
Multiply the second equation in the system (9) by −16, and add to the first equation in
the system (9).
12A − 4C
=
892
63
B
=
23
63
C
=
8
63
(4.10)
Multiply the first equation in the system (10) by 14 .
3A − C
=
223
63
B
=
23
63
C
=
8
63
(4.11)
Add the third equation in the system (11) to the first equation in the system (11).
3A =
11
3
B
=
23
63
C
=
8
63
(4.12)
Multiply the first equation in the system (12) by 13 .
=
11
9
B =
23
63
C
8
63
A
=
(II)
4.1. SOLVING SYSTEMS OF LINEAR EQUATIONS (REVIEW)
85
8
After checking with the system (I), A = 11
, B = 23
, and C = 63
indeed satisfy the three
9
63
, 23 , 8 .
equations in system (I). Therefore, the solution of the system is 11
9 63 63
Let us look at the system (I) in the following way.
4 −1 5
3
−4 0
7
−4
1 −2 4
1
(III)
The first row represents the first equation of the system (I): the first entry is the coefficient
of A; the second entry is the coefficient of B; the third entry is the coefficient of C; and
the last entry is the right side of the first equation. The second row represents the second
equation of the system (I); and the third row represents the third equation of the system
(I). The system in (III) is called the matrix form of the system in (I).
If we write the matrix form of the system in (II), then we get:
1 0 0
0 1 0
0 0 1
11
9
23
63
8
63
(IV)
The matrix (IV ) is called the reduced raw echelon form (rref) of the matrix (III).
If you have noticed the algorithmic nature of the process of going from matrix (III) to
matrix (IV ), then it may have occurred to you that this process can be programed into
a calculator to speedily find the solution of a system of linear equations.
In fact, there is a command in TI-83 called “rref” that is the name of the program to find
the reduced raw echelon form of a matrix in TI-83.
Exercise. Suppose A, B, and C are real numbers. Find the solution of the system
−A + 2B − 3C
= 7
4A − B + C
= 4
A − 2B + 4C
= 6
86
CHAPTER 4. PARTIAL FRACTION DECOMPOSITION
by using the “rref ” command in TI-83. Write your solution as a triple of fractions. That
is, decimal approximations are unacceptable.
4.2
Partial Fraction Decomposition: Linear Factors
Consider the following two examples of the addition of two rational expressions. You may
have learned in grades 4 and 5, how to add fractions. Then you may have learned in high
school that the addition of fractional expression are similar to the addition of fractions.
Example. Find
14
3
+
.
x − 13 x + 14
The basic idea behind the addition of fractions is that the fractions can be put on an
“equal footing”. Once that is done the addition of fractions is reduced to an addition of
positive integers that you may have learned in grade 1 and 2. We will do nothing different
here.
3
14
3(x + 14)
14(x − 13)
+
=
+
x − 13 x + 14
(x − 13)(x + 14) (x − 13)(x + 14)
=
3(x + 14) + 14(x − 13)
(x − 13)(x + 14)
=
17x − 140
(x − 13)(x + 14)
Example. Find
3
4
5
+
+
.
2
x − 3 (x − 3)
(x − 3)3
3
4
5
3(x − 3)2 4(x − 3)
5
+
+
=
+
+
x − 3 (x − 3)2 (x − 3)3
(x − 3)3
(x − 3)3 (x − 3)3
=
3(x − 3)2 + 4(x − 3) + 5
(x − 3)3
=
3(x2 − 6x + 9) + 4x − 12 + 5
(x − 3)3
4.2. PARTIAL FRACTION DECOMPOSITION: LINEAR FACTORS
=
87
3x2 − 14x + 20
(x − 3)3
Recall the use of the distributive property with polynomials and the factoring of polynomials. For example, we can multiply (x − 2)(x + 3) by using the distributive property.
That is, (x − 2)(x + 3) = x2 + x − 6. Now if we want to factor x2 + x − 6, we have to
devise a method to undo what distributive property did to (x − 2)(x + 3). This should
be familiar to you.
We will ask similar questions now.
1. Can you write
17x−140
(x−13)(x+14)
2. Can you write
3x2 −14x+20
(x−3)3
as a sum of fractional expressions?
as a sum of fractional expressions?
If we have not seen the two previous examples, then at the moment we do not know what
to do. Writing a given fractional expression as a sum of fractional expressions is known
as partial fraction decomposition (PFD).
In the first example, we say the linear factors (x − 13) and (x + 14) are non-repeating
factors. In the second example, we say (x − 3) is a repeating linear factor. In fact, (x − 3)
is repeating 3 times.
The following useful theorem is the third theorem that we have encountered that we
cannot prove in this class.
88
CHAPTER 4. PARTIAL FRACTION DECOMPOSITION
PFD with Linear Factors Theorem. Suppose f (x) = p(x)
is a rational function,
q(x)
where, p(x) and q(x) are polynomials and the degree of p(x) < the degree of q(x).
Suppose q(x) can be completely factored into linear factors.
1. For each non-repeating linear factor of q(x), write a fractional expression of the
form (Ak )/(linear factor), where Ak , etc., are constants.
2. For each repeating linear factor that repeats n times, write n factors of the form
(B1 )/(linear factor), (B2 )/(linear factor)2 , . . . (Bn )/(linear factor)n , where B1 ,
B2 , . . ., Bn , etc., are constants.
Then f (x) = sum of all fractional expressions in (1) and (2), and all those constants
in the numerators of fractional expressions are unique.
Example. Write the PFD for
3x + 5
, according to the PFD with Linear Factors Theorem.
(x − 13)(x + 14)
Solution. The degree of the numerator is 1, and the degree of the denominator is 2.
Therefore, the degree of the numerator is less than the degree of the denominator. (3x + 5)
and (x+14) are non-repeating linear factors. Therefore, the partial fraction decomposition
of the given fractional expression is:
3x + 5
A
B
=
+
,
(x − 13)(x + 14)
x − 13 x + 14
where A and B are constants that need to be determined. (We do not know how to find
the constants yet.)
Example. Write the PFD for
13x3 − 2x + 4
, according to the PFD with Linear Factors Theorem.
(x − 3)(x + 4)3
Solution. The degree of the numerator is 3 and the degree of the denominator is 4.
Therefore, the degree of the numerator is less than the degree of the denominator. (x − 3)
is a non-repeating linear factor and (x+4) is a repeating linear factor that repeats 3 times.
Therefore, the partial fraction decomposition of the given fractional expression is:
13x3 − 2x + 4
A2
A3
A1
A4
=
+
+
+
,
3
2
(x − 3)(x + 4)
x − 3 x + 4 (x + 4)
(x + 4)3
where A1 , A2 , A3 , and A4 are constants that need to be determined.
4.2. PARTIAL FRACTION DECOMPOSITION: LINEAR FACTORS
89
Let us say we want to find the constants in the previous two examples to complete the
tasks.
Example. Find the PFD for
3x + 5
, according to the PFD with Linear Factors Theorem.
(x − 13)(x + 14)
Solution.
3x + 5
A
B
=
+
,
(x − 13)(x + 14)
x − 13 x + 14
for some constants A and B.
A(x + 14) + B(x − 13)
(x − 13)(x + 14)
Ax + 14A + Bx − 13B
=
(x − 13)(x + 14)
(A + B)x + (14A − 13B)
=
(x − 13)(x + 14)
Right side =
According to the theorem, the fractional expression on the left side is equal to the fractional
expression on the right side. Now, both rational expressions on the left side and on the right
side have the same denominator. Therefore, numerators of those fractional expressions
must be equal to each other. The only way the two numerators can be equal to each other
is, if
3 = A+B
(4.13)
5 = 14A − 13B
The matrix form of the above system is:
1
3
1
14 −13 5
(4.14)
By solving the system of equations, we can find A and B. By using a (TI-83) calculator,
A = 44
and B = 37
.
27
27
Therefore, the PFD is:
3x + 5
44/27
37/27
=
+
.
(x − 13)(x + 14)
x − 13 x + 14
90
CHAPTER 4. PARTIAL FRACTION DECOMPOSITION
or
3x + 5
44
37
=
+
.
(x − 13)(x + 14)
27(x − 13) 27(x + 14)
Example. Find the PFD for
13x3 − 2x + 4
, according to the PFD with Linear Factors Theorem.
(x − 3)(x + 4)3
Solution.
A2
A3
13x3 − 2x + 4
A1
A4
+
+
=
+
,
3
2
(x − 3)(x + 4)
x − 3 x + 4 (x + 4)
(x + 4)3
where, A1 , A2 , A3 , and A4 are constants.
Right side
=
A2 (x − 3)(x + 4)2 A3 (x − 3)(x + 4)
A4 (x − 3)
A1 (x + 4)3
+
+
+
3
3
3
(x − 3)(x + 4)
(x − 3)(x + 4)
(x − 3)(x + 4)
(x − 3)(x + 4)3
=
A1 (x3 + 12x2 + 48x + 64) + A2 (x − 3)(x2 + 8x + 16) + A3 (x2 + x − 12) + A4 x − 3A4
(x − 3)(x + 4)3
(A1 + A2 )x3 + (12A1 + 5A2 + A3 )x2 + (48A1 − 8A2 + A3 + A4 )x
+ 64A1 − 48A2 − 12A3 − 3A4
=
(x − 3)(x + 4)3
By comparing fractional expressions, we get the following set of linear equations.
13
= A1 + A2
0
= 12A1 + 5A2 + A3
(4.15)
−2 = 48A1 − 8A2 + A3 + A4
4
= 64A1 − 48A2 − 12A3 − 3A4
The matrix form of the above system is:
1
0
0 13
1
5
1
0
0
12
48 −8
1
1
−2
64 −48 −12 −3 4
(4.16)
4.2. PARTIAL FRACTION DECOMPOSITION: LINEAR FACTORS
By using a (TI-83) calculator, we get, A1 =
349
,
343
A2 =
4110
,
343
A3 = − 3534
and A4 =
49
Therefore, the PFD is:
13x3 − 2x + 4
349
4110
3534
820
=
+
−
+
.
3
2
(x − 3)(x + 4)
343(x − 3) 343(x + 4) 49(x + 4)
7(x + 4)3
91
820
.
7
92
CHAPTER 4. PARTIAL FRACTION DECOMPOSITION
4.3
Partial Fraction Decomposition: Irreducible
Quadratic Factors
PFD with Irreducible Quadratic Factors Theorem. Suppose f (x) = p(x)
is
q(x)
a rational function, where p(x) and q(x) are polynomials and the degree of p(x) <
the degree of q(x). Suppose q(x) can be completely factored into linear factors and
irreducible quadratic factors.
1. For each linear factor, follow the PFD with Linear Factors Theorem.
2. For each non-repeating irreducible quadratic factor of q(x), write a fractional
expression of the form (Ak x + Bk )/(linear factor), where Ak , Bk , etc., are constants.
3. For each repeating irreducible quadratic factor that repeats n times, write n factors of the form (C1 x + D1 )/(quadratic factor), (C2 x + D2 )/(quadratic factor)2 ,
. . . (Cn x + Dn ))/(quadratic factor)n , where C1 , D1 , C2 , D2 , . . ., Cn , Dn etc.,
are constants.
Then f (x) = sum of all fractional expressions in (1), (2) and (3), and all those
constants in the numerators of fractional expressions are unique.
Example. Find the PFD of
x2 − 3x + 1
.
(x − 1)(x2 − x + 1)2
Solution. x2 − x + 1 is an irreducible quadratic factor over R, because the discriminant
is negative. Therefore, by the PFD with Quadratic Factors Theorem,
x2 − 3x + 1
A
Bx + C
Dx + E
=
+ 2
+ 2
,
2
2
(x − 1)(x − x + 1)
x − 1 x − x + 1 (x − x + 1)2
for some real constants A, B, C, D, and E.
Right side
=
A(x2 − x + 1)2
(Bx + C)(x − 1)(x2 − x + 1)
(Dx + E)(x − 1)
+
+
2
2
2
2
(x − 1)(x − x + 1)
(x − 1)(x − x + 1)
(x − 1)(x2 − x + 1)2
4.3. PARTIAL FRACTION DECOMPOSITION: IRREDUCIBLE QUADRATIC
FACTORS
4
3
2
3
93
2
A(x − 2x + 3x − 2x + 1) + (Bx + C)(x − 2x + 2x − 1) + (Dx + E)(x − 1)
(x − 1)(x2 − x + 1)2
4
3
2
Ax − 2Ax + 3Ax − 2Ax + A + Bx4 − 2Bx3 + 2Bx2 − Bx + Cx3
− 2Cx2 + 2Cx − C + Dx2 − Dx + Ex − E
=
(x − 1)(x2 − x + 1)2
4
(A + B)x + (−2A − 2B + C)x3 + (3A + 2B − 2C + D)x2
+ (−2A − B + 2C − D + E)x + (A − C − E)
=
(x − 1)(x2 − x + 1)2
=
By comparing fractional expressions, we get the following set of linear equations.
0
= A+B
0
= −2A − 2B + C
1
= 3A + 2B − 2C + D
(4.17)
−3 = −2A − B + 2C − D + E
1
= A−C −E
The matrix form of the
1
0
1
−2 −2 1
3
2 −2
−2 −1 2
1
0 −1
above system is:
0
0
0
0
0
0
1
0
1
−1 1 −3
0 −1 1
By using a (TI-83) calculator we get, A = −1, B = 1, C = 0, D = 2 and E = −2.
Therefore, the PFD is:
−1
x
2x − 2
x2 − 3x + 1
+ 2
=
+ 2
2
2
(x − 1)(x − x + 1)
x − 1 x − x + 1 (x − x + 1)2
(4.18)
94
CHAPTER 4. PARTIAL FRACTION DECOMPOSITION
Exercise. Find the PFD of
x3 − 2x2 − x + 1
.
(x + 1)(x − 1)2 (x2 + 1)2
Part II
Trigonometry
95
Chapter 5
Trigonometry of Angles
5.1
Angles
Consider two fixed rays with a common vertex O on a plane. Now imagine another ray,
we call it a free ray, with the same vertex, which is free to rotate around O. Suppose the
free ray rotates from one fixed ray to the other fixed ray. The region generated by the
sweeping free ray between the two fixed rays is called an angle. The point O is called
the vertex of the angle; the two fixed rays are called the sides of the angle: the fixed ray
where the rotation began is called the initial side of the angle; and the fixed ray where
the rotation ended is called the terminal side of the angle.
You should realize that there are infinitely many angles with the same vertex, the same
initial side and the same terminal side. The following is another angle with the vertex O,
the same initial side and the same terminal side as the previous angle.
97
98
CHAPTER 5. TRIGONOMETRY OF ANGLES
When you rotate the free ray more that one full cycle from the initial ray to the terminal
ray, then you get angles with overlapping regions. It is difficult to visualize overlapping
regions. Therefore, from now on, we will indicate angles only by rotation.
A plane with the familiar xy coordinate system is known as the xy-plane. If we use a rigid
transformation to move an angle so that its vertex coincides with the origin O and its
initial side coincides with the positive x-axis, then we say that the angle is in the standard
position. The following is another angle with the vertex O, the same initial side and the
same terminal side as the previous angle.
When you place angles in standard position, the angles with the same terminal side is
known as co-terminal angles.
5.2
Degree Measure of an Angle
If we can somehow measure the “amount of rotation”, then we can distinguish all the
different angles with the same vertex, the same initial side and the same terminal side.
About 4000 years ago, the great civilizations of Middle East devised a method to measure
angles. We use this measuring system developed by the Babylonians even today. The
Babylonians had a base 60 number system. (It is possible that they used this system
because it was easy to write fractions like 12 , 13 , 14 , 15 and 16 in this system. For example,
1
= 30 units, 31 = 20 units, 41 = 15 units, 51 = 12 units and 16 = 10 units, in base
2
5.2. DEGREE MEASURE OF AN ANGLE
99
60 system.1 ) Their ingenious method of measuring angles can be described as follows.
Consider a circular disc. Partition the circumference of this into 360 equal parts by
drawing tick marks. Then draw rays through each tick mark from O. The amount of
rotation between any two consecutive rays is called 1 degree. By identifying tick marks
with numbers 0, 1, 2, · · · , 360, now we have a tool to measure the rotation of an angle.
To measure the rotation of an angle, place the circular disc on the same plane where the
angle is so that the center of the disc coincides with O and the 0 tick mark is on the initial
side.
120
90 80
110 100
70
60
130
140
50
40
150
30
160
20
170
10
180
0
O
190
350
200
340
210
330
220
230
320
310
240
250 260
290
270 280
300
If the angle is less than a full counterclockwise rotation and if the terminal side lands
on a tick mark (say, on 45)2 , then we say the measure of the angle is 45 degrees. If the
angle is 45 degrees more than one counterclockwise rotation, then we say the measure of
1
Read “Exact Sciences in antiquity” by Otto Neugebauer, if you are interested.
Most probably, the terminal side will not land on any tick mark. Then we use the tick mark closest
to the terminal side.
2
100
CHAPTER 5. TRIGONOMETRY OF ANGLES
the angle is 360 + 45 = 405 degrees. In this manner, we can assign a degree measure
to any angle with counterclockwise rotation. We consider clockwise rotations as negative
rotations and assign a negative degree measure to those angles.
We usually use a little circle as a superscript to denote degrees. For example, 45◦ stands
for 45 degrees.
−315◦ angle
Notice that we have selected a circle with center O when we defined the degree measure.
There was no mention about the radius of the circle. That is, the chosen circle can have
any radius as long as the center is at O. As you can imagine longer the radius, longer
the circumference. Since we are partitioning the circle into exactly 360 equal parts, the
longer the radius, the longer each part. Seemingly miraculously, for any given angle, the
number of parts in an arc of a circle subtended by the angle is the same for any circle, no
matter what the radius is.
5.3. RADIAN MEASURE OF AN ANGLE
120
130
140
90 80
110 100
70
120
90 80
110 100
70
60
50
40
60
130
140
150
101
50
150
160
30
40
30
160
170
170
180
180
190
190
10
0
0
350
350
340
210
210
10
O
200
200
20
20
340
330
220
230
220
230
320
310
240
240
250 260
290
270 280
320
310
300
250 260
290
270 280
330
300
You may have learned in high school that “all circles are similar”. That is the reason
behind this seeming miracle. In that sense, the degree measure of an angle is unique.
That is, there is only one degree measure for any given angle.
See also the Paper Folding Experiment.
5.3
Radian Measure of an Angle
There is another more modern angle measure known as the radian measure.
Consider an angle in standard position so that the rotation is counterclockwise. Once
again, place a circular disk with radius r (in distance units) so that its center is O.
Suppose the arc-length of the arc subtended by the angle is s in distance units. The ratio
s
is called the radian measure of the angle. The radian measure of an angle is also unique
r
since all circles are similar.
The circle with center (0, 0) and radius 1 unit on the xy-plane is called the unit circle.
102
CHAPTER 5. TRIGONOMETRY OF ANGLES
Since the radius of the circle we pick is irrelevant when we measure an angle in the
standard position (as long as the center of the circle is O), we can use the unit circle to
measure angles.
If the arc on the unit circle subtended by an angle in a standard position has an arc-length
of 1 unit, then the radian measure of the angle is 1 radian.
5.4
Relationship between the Degree Measure and
the Radian Measure
You may have learned in middle school or high school that the circumference of a circle
with radius r is 2πr. Accordingly, the circumference of a unit circle is 2π. By the definition
of the radian measure, the radian measure of a full angle is 2π. When the circumference
2π
of the unit circle is partitioned into 360 equal parts, then the length of one part is 360
or
π
π
◦
. Therefore, the radian measure of an angle of 1 is 180 ; the radian measure of an angle
180
2π
3π
of 2◦ is 180
; the radian measure of an angle of 3◦ is 180
; the radian measure of an angle of
−3π
nπ
◦
−3 is 180 , etc; and the radian measure of an angle of n◦ is 180
, where n is an integer.
It is a convention to use Greek lowercase letters to represent angles. For example, α
(alpha), β (beta), γ (gamma), θ, (theta) are a few such letters that are often used to
represent angles.
Consider the following angles. Let θ1 be the angle in the standard position, where the
initial and the terminal sides coincide. Suppose we partition the circumference of the unit
circle into 12 equal parts and one of the partition tick-marks coincides with the positive
x-axis. Let θ2 be the angle in the standard position, where the terminal side passes
through the first tick-mark in the counterclockwise direction. Suppose we partition the
circumference of the unit circle into 8 equal parts and one of the partition tick-marks
coincides with the positive x-axis. Let θ3 be the angle in the standard position, where
the terminal side passes through the first tick-mark in the counterclockwise direction.
Suppose we partition the circumference of the unit circle into 6 equal parts and one
of the partition tick-marks coincides with the positive x-axis. Let θ4 be the angle in
the standard position, where the terminal side passes through the first tick-mark in the
counterclockwise direction. Suppose we partition the circumference of the unit circle into
4 equal parts and one of the partition tick-marks coincides with the positive x-axis. Let
θ5 be the angle in the standard position, where the terminal side pass through the first
5.5. TRIGONOMETRIC NUMBERS OF ANGLES
103
tick-mark in the counterclockwise direction.
θ1
θ2
θ3
θ4
θ5
The following table lists the angle measure and the radian measure of the chosen angles.
(These angles will be known as “special angles”, for lack of a better term, from now on.)
Angle
Degree Measure
Radian Measure
θ1
0
0
θ2
30
π
6
θ3
45
π
4
θ4
60
π
3
θ5
90
π
2
5.5
Trigonometric Numbers of Angles
We will define two important numbers for a given angle θ in the standard position as
follows. Let P (a, b) be any chosen point on the terminal side of θ other than O. Let r be
the length of OP . We define sin θ, pronounced “sine theta”, as the ratio rb and we define
cos θ, pronounced “cosine theta”, as the ratio ar . The sin θ and the cos θ are two of the
six trigonometric numbers of θ that we are going to define for a given angle θ.
Notice that in the definition of sin θ, we are free to choose the point P on the terminal
side of the angle θ as long as P 6= O. Can the value of the number sin θ be different for
two different points P1 (a1 , b1 ) and P2 (a2 , b2 ) on the terminal side of the angle θ? We will
answer this question if the terminal side of θ lies in the third quadrant. Finding answers
to other quadrants and the axes will be left as an exercise.
Suppose the terminal side of θ is in the third quadrant. Then both b1 , b2 are negative.
Therefore, the sign of rb11 is the same as the sign of rb22 .
104
CHAPTER 5. TRIGONOMETRY OF ANGLES
O
P1 (a1 , b1 )
P2 (a2 , b2 )
Now drop perpendiculars from both P1 and P2 onto the x-axis. Let the feet of those
perpendiculars be Q1 and Q2 respectively.
Q2
Q1
O
P1 (a1 , b1 )
P2 (a2 , b2 )
The triangles OP1 Q1 and OP2 Q2 are similar by the AA criteria. Therefore, PP11QO1 = PP22QO2 .
1
1
That is, −b
= −b
. Therefore, the number sin θ is the same for both P1 and P2 . Since P1
r1
r1
and P2 are two arbitrary points on the terminal side of θ, this observation implies that,
by definition, the number sin θ is unique for any point selected on the terminal side of θ.
Exercise.
1.
2.
3.
4.
5.
6.
7.
Show
Show
Show
Show
Show
Show
Show
that
that
that
that
that
that
that
the
the
the
the
the
the
the
number
number
number
number
number
number
number
sin θ
sin θ
sin θ
sin θ
sin θ
sin θ
sin θ
is
is
is
is
is
is
is
unique
unique
unique
unique
unique
unique
unique
if
if
if
if
if
if
if
θ
θ
θ
θ
θ
θ
θ
is
is
is
is
is
is
is
in the first quadrant.
in the second quadrant.
in the fourth quadrant.
on the positive x-axis.
on the negative x-axis.
on the positive y-axis.
on the negative y-axis.
5.5. TRIGONOMETRIC NUMBERS OF ANGLES
105
You can show by similar means that the number cos θ is also unique for a given angle θ,
by definition.
It is customary to replace the name of the angle by its measure if we know the measure.
For example, we usually write sin π3 for sin θ, when θ has the measure π3 . We will also
loosely say θ = π3 .
Some of the theorems that you may have learned in a high school geometry class are going
to be very useful. The following is a list of high school geometric theorems. We will use
the following notation in these theorems. Consider two points A and B. We will use AB
to represent the line segment with endpoints A and B. We will use |AB| for the length
of AB. We will use LAB for the line containing A and B.
Angle Sum of a Triangle Theorem. The sum of the measures of the angles of a
triangle is 180◦ .
Equilateral Triangle Theorem. The measure of any angle of an equilateral triangle
is 60◦ , and vice versa.
Isosceles Triangle Theorem. The measures of angles facing congruent sides of an
isosceles triangle are equal, and vice versa.
Perpendicular Bisector Theorem. Let 4ABC be an isosceles triangle so that
AB ∼
= AC. Then the angle bisector of ∠A is the perpendicular bisector of BC, and
vice versa.
SAS Theorem. Let 4ABC and 4DEF are two triangles so that AB ∼
= DE, ∠B ∼
=
∼
∠E and BC = EF . Then the two triangles are congruent.
106
CHAPTER 5. TRIGONOMETRY OF ANGLES
Pythagorean Theorem. Let 4ABC be a right triangle so that AC is the hypotenuse.
Then |AC|2 = |AB|2 + |BC|2 .
Now we will derive the sine and cosine numbers of “special” angles. We will use the radian
measure for an angle in the following theorems.
Trigonometric Numbers of 0 Theorem.
1. sin 0 = 0
2. cos 0 = 1
Proof. Let θ be the given angle.
O
P (a, 0)
Since the measure of θ = 0, the terminal side of θ lies on the positive x-axis. Let P (a, 0)
be any arbitrary point on the terminal side of θ, where a 6= 0. Then r = |OP | = a, and,
by definition, sin 0 = a0 = 0. Also, cos 0 = ar , by definition. Since a 6= 0, ar = aa = 1.
Therefore, cos 0 = 1.
5.5. TRIGONOMETRIC NUMBERS OF ANGLES
Trigonometric Numbers of
π
6
107
Theorem.
1. sin π6 = 21
√
2. cos π6 = 23
Proof. Let θ be the angle with measure π6 . Let P (a, b) be an arbitrary point on the
terminal side of θ so that a 6= 0 and b 6= 0, and let |OP | = r.
P (a, b)
θ
O
Drop a perpendicular from P to the positive x-axis. Let the foot of this perpendicular be
R. The angle ∠ROP has the measure π6 because it is θ. Then the measure of the angle
∠OP R is π3 , since the angle ORP is a right angle and by the Angle Sum of a Triangle
Theorem.
P (a, b)
θ
O
R
Now extend P R to Q so that |P R| = |RQ|. Connect O and Q by a line segment.
108
CHAPTER 5. TRIGONOMETRY OF ANGLES
P (a, b)
θ
O
R
Q
By the SAS theorem, the triangle 4OP R and the triangle 4OQR are congruent. (P R ∼
=
QR, by construction; OR is a common side; and angles ∠ORP and ∠ORQ are right
angles.) Therefore, ∠OQR has measure π3 and the triangle 4OP Q is an equilateral
triangle. Then |P Q| = r, since |OP | = r. Also, LOR is the perpendicular bisector of P Q.
Therefore, |P R| = 12 r. By the Pythagorean Theorem, |OR|2 = |OP |2 − |P R|2 . Therefore,
√
√
|OR|2 = r2 − 41 r2 = 43 r2 . That is, |OR| = 23 r. Therefore, a = 23 r and b = 21 r. By
√
definition, sin θ = rb = 12 and cos θ = ar = 23 .
Trigonometric Numbers of
π
4
Theorem.
1. sin π4 = √12
2. cos π4 = √12
Proof. Let θ be the angle with measure π4 . Let P (a, b) be a point on the terminal side of
θ so that both a and b are positive and let |OP | = r.
5.5. TRIGONOMETRIC NUMBERS OF ANGLES
109
P (a, b)
θ
O
Drop a perpendicular from P to the x-axis so that R is the foot of the perpendicular.
The angle ∠OP R has the same measure as θ as a result of the Angle Sum of a Triangle
Theorem.
P (a, b)
θ
O
R
Then 4OP R is an isosceles triangle with OR ∼
= P R. This means a = b, since the
coordinates of P are (a, b). By the Pythagorean Theorem, r2 = a2 + a2 . Therefore,
a = b = √12 r. By definition, sin θ = rb = √12 and cos θ = ar = √12 .
Trigonometric Numbers of
1. sin π3 =
2. cos π3 =
π
3
Theorem.
√
3
2
1
2
Proof. Let θ be the angle with measure π3 . Let P (a, b) be a point on the terminal side of
θ so that both a and b are positive and let |OP | = r.
110
CHAPTER 5. TRIGONOMETRY OF ANGLES
P (a, b)
θ
O
Drop a perpendicular from P to the x-axis so that R is the foot of the perpendicular.
Extend OR to Q so that |OR| = |RQ|. Connect P and Q by a line segment.
P (a, b)
θ
O
R
Q
The line LP R is the perpendicular bisector of OQ. Therefore, LP R is the angle bisector of
∠OP Q. The angle ∠OP R has the measure π6 by the Angle Sum of a Triangle Theorem
on the triangle 4OP R. Then, ∠RP Q has the measure π6 and therefore, ∠OP Q has the
measure π3 . Then by the Angle Sum of a Triangle Theorem, ∠P QO has the measure π3
and the triangle P OQ is an equilateral triangle, by the Equilateral Triangle Theorem.
Then |OQ| = r and |OR| = 12 r. By the Pythagorean Theorem, |P R|2 = |OP |2 − |OR|2 .
√
√
That is, |P R|2 = r2 − 41 r2 = 34 r2 . Therefore, |P R| = 23 . By definition, sin θ = rb = 23
and cos θ = ar = 21 .
5.5. TRIGONOMETRIC NUMBERS OF ANGLES
Trigonometric Numbers of
π
2
111
Theorem.
1. sin π2 = 1
2. cos π2 = 0
Proof. Let θ be the given angle. Let P (0, b) be a point on the terminal side of θ, where
b 6= 0. Let |OP | = r. Then r = b.
P (0, b)
O
By definition, sin π2 =
b
r
=
b
b
= 1 since b 6= 0. Also, cos π2 =
a
r
=
0
b
= 0, by definition.
The results of the last five theorems are summarized in the following table. That is, the
sine and cosine trigonometric numbers of the special angles are:
θ
sin θ
0
0
cos θ
1
√
3
2
π
6
1
2
π
4
√1
2
π
3
√1
2
√
3
2
π
2
1
0
1
2
Here is another theorem that you may have learned in high school.
112
CHAPTER 5. TRIGONOMETRY OF ANGLES
The Two Dimensional Distance Formula Theorem. Let P (x1 , y1 ) and Q(x1 , y1 )
p
be two points. Then the distance between P and Q is (x2 − x1 )2 + (y2 − y1 )2 .
(You can prove the Distance Formula Theorem using the Pythagorean Theorem.)
Example. Suppose an angle θ is in the standard position and P (−2, 3) is a point on the
terminal side of θ. Find sin θ and cos θ.
p
Answer. Let |OP | = r. Then by the Distance Formula Theorem, r = (−2 − 0)2 + (3 − 0)2 =
√
13. Therefore, sin θ = √313 and cos θ = √−2
.
13
In the previous example, the terminal side of the given angle θ lies in the second quadrant.
It turned out that sin θ > 0 and cos θ < 0. This is in fact, a true statement for any angle
in standard position if the terminal side lies in the second quadrant. The following is a
theorem that you can prove using just the definitions of sin θ and cos θ.
We will loosely say “the angle is in the second quadrant” if the angle is in the standard
position and its terminal side lies in the second quadrant.
Theorem. Let θ be an angle in standard position.
1.
2.
3.
4.
If
If
If
If
θ
θ
θ
θ
is
is
is
is
in
in
in
in
the
the
the
the
first quadrant, then sin θ > 0 and cos θ > 0.
second quadrant, then sin θ > 0 and cos θ < 0.
third quadrant, then sin θ < 0 and cos θ < 0.
fourth quadrant, then sin θ < 0 and cos θ > 0.
By the definitions of sin θ and cos θ, for a given angle θ in a standard position, it does not
matter what point P we select on the terminal side to compute those numbers. We could
choose P as the point where the terminal side of θ intersects the unit circle. Since the
radius of the unit cycle is 1, r = 1. Therefore, for a given angle θ in standard position,
if we choose the point of intersection of the terminal side and the unit circle as P (a, b),
then sin θ = rb = b, cos θ = ar = a. That is, the coordinates of P are (cos θ, sin θ).
5.5. TRIGONOMETRIC NUMBERS OF ANGLES
113
In the following figure, the measure of the angle is written on the terminal side of the
angle, and the coordinates of the point on the unit circle is shown. We have used the
trigonometric numbers of the special angles in this figure.
π
2
π
3
π
4
(0, 1)
√ 3
1
,
2 2
√1 , √1
2
2
√
3 1
,
2 2
π
6
(1, 0)
0
With this figure in place, we can find trigonometric numbers of more angles related to the
special angles.
The reflection of the terminal side of the angle π4 with respect to y-axis is the terminal
side of the angle 3π
. Therefore, sin 3π
= √12 and cos 3π
= √12 .
4
4
4
The reflection of the terminal side of the angle π4 with respect to x-axis is the terminal
side of the angle 7π
. Therefore, sin 7π
= − √12 and cos 7π
= √12 .
4
4
4
The reflection of the terminal side of the angle 3π
with respect to x-axis is the terminal
4
5π
5π
1
side of the angle 4 . Therefore, sin 4 = − √2 and cos 7π
= − √12 .
4
114
CHAPTER 5. TRIGONOMETRY OF ANGLES
These results are given in the following figure.
3π
4
π
4
− √12 , √12
√1 , √1
2
2
− √12 , − √12
√1 , − √1
2
2
5π
4
7π
4
The reflection of the terminal side of the angle π6 with respect to y-axis is the terminal
√
3
5π
1
5π
side of the angle 5π
.
Therefore,
sin
=
and
cos
=
−
.
6
6
2
6
2
The reflection of the terminal side of the angle π6 with respect to x-axis is the terminal
√
3
11π
1
11π
side of the angle 11π
.
Therefore,
sin
=
−
and
cos
=
.
6
6
2
6
2
with respect to x-axis is the terminal
The reflection of the terminal side of the angle 5π
6
√
3
7π
7π
1
side of the angle 6 . Therefore, sin 6 = − 2 and cos 7π
=
−
.
6
2
These results are given in the following figure.
5π
6
π
6
√ − 23 , 21
√
−
3
, − 12
2
√
3 1
,
2 2
√
3
, − 21
2
7π
6
The reflection of the terminal side of the angle
11π
6
π
3
with respect to y-axis is the terminal
5.5. TRIGONOMETRIC NUMBERS OF ANGLES
side of the angle
2π
.
3
Therefore, sin 2π
=
3
√
3
2
115
and cos 2π
= − 12 .
3
The reflection of the terminal side of the angle π3 with respect to x-axis is the terminal
√
3
5π
side of the angle 5π
.
Therefore,
sin
=
−
and cos 5π
= 12 .
3
3
2
3
The reflection of the terminal side of the angle 2π
with respect to x-axis is the terminal
3
√
3
4π
4π
side of the angle 3 . Therefore, sin 3 = − 2 and cos 4π
= − 12 .
3
These results are given in the following figure.
π
3
2π
3
√ 1
− 2 , 23
− 21 , −
4π
3
√
3
2
√ 1
, 3
2 2
√ 3
1
,
−
2
2
5π
3
The following is a figure that contains all of our findings and the trigonometric values of
angles in the standard position.
116
CHAPTER 5. TRIGONOMETRY OF ANGLES
π
2
π
3
2π
3
3π
4
5π
6
π
π
4
(0, 1)
− 12 ,
√
3
2
√ 3
1
,
2 2
− √12 , √12
√ − 23 , 12
√1 , √1
2
2
√
7π
6
√
3
, − 21
2
−
π
6
3 1
,
2 2
(−1, 0)
0
(1, 0)
√
3
, − 21
2
− √12 , − √12
√ − 12 , − 23
5π
4
√1 , − √1
2
2
√ 3
1
,
−
2
2
7π
4
(0, −1)
4π
3
5π
3
3π
2
11π
6
Chapter 6
Trigonometric Functions
We will use the radian measure for angles in this section. We will also use θ to represent
the radian measure of the angle θ. Since the radian measure of a given angle is a unique
number, θ is a number. By the definition of sin θ, there is only one number sin θ, for a
given angle θ. Let f (θ) = sin θ. Then f (θ) is a function of θ, because for each angle θ
there is exactly one sin θ.
Consider a θy coordinate system (In this system, θ-axis plays the role usually played by
the x-axis. As a matter of fact, we could replace θ with x and use the usual xy coordinate
system. But we will wait until we are a little more comfortable with sine and cosine
functions before making this move.)
6.1
Sine Function
The collection of all points (θ, sin θ) on the θy-plane is called the graph of the function
f (θ) = sin θ.
One observation about the graph of f (θ) = sin θ is extremely useful. Since sin θ is the
y-coordinate of the intersection of the terminal side and the unit circle, the values of the
sine function are the same for co-terminal angles. Co-terminal angles differ from each
other by an integer multiple of a full cycle. That is, if θ and α are co-terminal angles,
then there is an integer k so that α = 2kπ + θ. Therefore,
sin(2kπ + θ) = sin θ for any integer k.
That is, the graph of f (θ) = sin θ in the interval [2k1 π, 2(k1 + 1)π], for a given integer k1 ,
is identical to the graph of f (θ) = sin θ in the interval [2kπ, 2(k + 1)π], for any integer k.
117
118
CHAPTER 6. TRIGONOMETRIC FUNCTIONS
Therefore, if we can sketch the graph of f (θ) = sin θ in the interval [0, 2π], then we know
the graph of f (θ) = sin θ for the entire θ-axis.
We will use the sine numbers of special angles and the reflections of special angles to get
a rough sketch of the graph of f (θ) = sin θ in the interval [0, 2π]. The following table
contains sine numbers of special angles and the reflections of special angles.
θ
sin θ
θ
0
π
2
0
θ
1
π
√
0
7π
6
− 12
3π
4
√1
2
5π
4
− √12
5π
6
1
2
4π
3
1
2
2π
3
π
4
√1
2
√
3
2
θ
sin θ
3π
2
−1
sin θ
3
2
π
6
π
3
sin θ
√
−
3
2
√
3
2
5π
3
−
7π
4
− √12
11π
6
− 21
2π
0
The sketch of the graph of f (θ) = sin θ in the interval [0, 2π] is given below.
y
1
π π π
6 4 3
π
π
2
2π
3π
2
θ
−1
The shape of the graph of f (θ) = sin θ over [0, 2π] is congruent to the shape of the graph
of f (θ) = sin θ over [2kπ, 2(k + 1)π], for any integer k, by the definition of sin θ on the
unit circle.
y
1
−2π
π
−π
2π
3π
4π
θ
−1
The graph of f (θ) = sin θ contains repeating patterns. Clearly, the portion of the graph
of f (θ) = sin θ over [0, 2π] is a repeating pattern.
6.1. SINE FUNCTION
119
y
1
π
−π
−2π
2π
3π
4π
θ
−1
The portion of the graph of f (θ) = sin θ over [−π/2, 3π/2] is also a repeating pattern.
y
1
π
−π
−2π
2π
3π
4π
θ
−1
The portion of the graph of f (θ) = sin θ over [−2π, 2π] is also a repeating pattern.
y
1
−2π
−π
−1
π
2π
3π
4π
θ
It is not difficult to see that there are infinitely many repeating patterns on the graph
of f (θ) = sin θ. If the graph of a function contains repeating patterns, then we say the
function is periodic. The length of the smallest interval over a pattern of the graph resides
is called the period of a periodic function. That is, if p is the period of a periodic function
f , then p is the smallest value with the property: for any number α, f (p + α) = f (α).
We already know that sin(2kπ + θ) = sin θ, for any integer k and for any number θ.
120
CHAPTER 6. TRIGONOMETRIC FUNCTIONS
Exercise.
1. Prove that the period of f (θ) = sin θ is 2π.
2. Prove that the maximum value of f (θ) = sin θ is 1.
3. Prove that the minimum value of f (θ) = sin θ is −1.
Suppose a periodic function has a maximum value and a minimum value. One half of
(the maximum value − the minimum value) of a periodic function is called the amplitude
of the periodic function.
Exercise.
1. Prove that the amplitude of f (θ) = sin θ is 1.
2. Prove that the domain of f (θ) = sin θ is (−∞, ∞) and the range is [−1, 1].
It should be clear to you that if we can sketch the portion of the graph of a periodic
function over an interval with a length equal to the period, then we can get the rest of the
graph of the function. From now on, we will concentrate our attention on only a portion
of the graph a periodic function over an interval whose length is the period of the periodic
function. For the sine function, we will select the interval [0, 2π]. We will loosely say that
we are sketching the graph of the function over a period.
y
1
π
2
π
3π
2
2π
θ
−1
The following are a few important observations of the above graph.
1. The sine function has zeros at 0, π, and 2π in [0, 2π].
2. The sine function has the maximum value at π2 in [0, 2π].
in [0, 2π].
3. The sine function has the minimum value at 3π
2
We say a function f is symmetrical with respect to the vertical line x = α in an interval
[a, b] if f (θ − α) = f (θ + α) in [a, b].
6.1. SINE FUNCTION
121
Exercise.
1. Prove that f (θ) = sin θ is symmetrical with respect to x =
y
π
2
in the interval [0, π].
1
π
2
−α
π
2
π
2
θ
+α
−1
2. Prove that f (θ) = sin θ is symmetrical with respect to x =
y
3π
2
in the interval [π, 2π].
1
3π
2
−α
3π
2
3π
2
+α
θ
−1
Example. Identify the amplitude, the period, and sketch the graph of f1 (θ) = 3 sin θ over
one period.
Answer. The function value of f1 at any given θ is three times the value of sin θ for any
θ.
θ
sin θ
3 sin θ
0
0
0
π
2
1
3
π
0
0
3π
2
−1
−3
2π
0
0
122
CHAPTER 6. TRIGONOMETRIC FUNCTIONS
y
3
π
2
π
3π
2
θ
2π
−3
The amplitude of f1 is 3 and the period is 2π.
Example. Identify the amplitude, the period, and sketch the graph of f2 (θ) = sin 3θ over
one period.
Answer. Let α = 3θ. Then θ = α3 .
θ=
α
3
α
sin α
sin 3θ
0
0
0
0
π
2
1
π
6
1
π
0
π
3
0
3π
2
−1
π
2
−1
2π
0
2π
3
0
y
1
π
6
−1
π
3
π
2
2π
3
θ
6.1. SINE FUNCTION
123
The amplitude of f2 is 1 and the period is
2π
.
3
Example. Identify the amplitude, the period, and sketch the graph of f3 (θ) = 3 sin 3θ
over one period.
Answer. Let α = 3θ. Then θ = α3 .
θ=
α
3
α
sin α
3 sin 3θ
0
0
0
0
π
2
1
π
6
3
π
0
π
3
0
3π
2
−1
π
2
−3
2π
0
2π
3
0
y
3
π
6
−3
π
3
π
2
2π
3
θ
124
CHAPTER 6. TRIGONOMETRIC FUNCTIONS
The amplitude of f3 is 3 and the period is
2π
.
3
Example. Identify the amplitude, the period, and sketch the graph of f4 (θ) = sin(θ − π3 )
over one period.
Answer. Let α = θ − π3 . Then θ = α + π3 .
θ =α+
π
3
sin(θ − π3 )
α
sin α
0
0
π
3
0
π
2
1
5π
6
1
π
0
4π
3
0
3π
2
−1
11π
6
−1
2π
0
7π
3
0
y
1
π
3
5π
6
4π
3
11π
6
7π
3
θ
−1
The amplitude of f4 is 1 and the period is 2π.
Notice that if the graph of the sine function is shifted to the right by π3 , then we get the
graph of f4 (θ) = sin(θ − π3 ). We say + π3 is the phase shift of f4 .
Example. Identify the amplitude, the period, and sketch the graph of f5 (θ) = sin(θ + π3 )
over one period.
Answer. Let α = θ + π3 . Then θ = α − π3 .
6.1. SINE FUNCTION
125
π
3
θ =α−
sin(θ + π3 )
α
sin α
0
0
− π3
0
π
2
1
π
6
1
π
0
2π
3
0
3π
2
−1
7π
6
−1
2π
0
5π
3
0
y
1
− π3
π
6
2π
3
7π
6
5π
3
θ
−1
The amplitude of f5 is 1 and the period is 2π.
Notice that if the graph of the sine function is shifted to the left by π3 (or to the right by
− π3 ), then we get the graph of f5 (θ) = sin(θ + π3 ). We say the phase shift of f5 is − π3 .
Example. Identify the amplitude, the period, the phase shift, and sketch the graph of
f6 (θ) = 3 sin 3(θ + π3 ) over one period.
Answer. Let α = 3(θ + π3 ). Then θ =
α
sin α
α
3
3 sin 3(θ + π3 )
0
0
0
− π3
0
0
π
2
1
π
6
− π6
1
3
π
0
π
3
0
0
0
3π
2
−1
π
2
π
6
−1
−3
2π
0
2π
3
π
3
0
0
−
π
3
− π3 .
sin 3(θ + π3 )
θ=
α
3
α
3
126
CHAPTER 6. TRIGONOMETRIC FUNCTIONS
y
3
− π3 − π6
π
6
π
3
θ
−3
The amplitude of f6 is 3, the period is
6.2
2π
,
3
and the phase shift is − π3 .
Cosine Function
The collection of all points (θ, cos θ) on the θy-plane is called the graph of the function
f (θ) = cos θ.
Since cos θ is the x-coordinate of the intersection of the terminal side and the unit circle,
the values of the cosine function are the same for co-terminal angles. Each co-terminal
angle differs from each other by an integer multiple of a full cycle. That is, if θ and α are
co-terminal angles, then there is an integer k so that α = 2kπ + θ. Therefore,
cos(2kπ + θ) = cos θ for any integer k.
That is, the graph of f (θ) = cos θ in the interval [2k1 π, 2(k1 + 1)π], for a given integer k1 ,
is identical to the graph of f (θ) = cos θ in the interval [2kπ, 2(k + 1)π], for any integer k.
6.2. COSINE FUNCTION
127
Therefore, if we can sketch the graph of f (θ) = cos θ in the interval [0, 2π], then we know
the graph of f (θ) = cos θ for the entire θ-axis.
We will use the cosine numbers of special angles and the reflections of special angles to
get a rough sketch of the graph of f (θ) = cos θ in the interval [0, 2π]. The following table
contains the cosine numbers of special angles and the reflections of special angles.
θ
cos θ
θ
1
π
2
0
√
cos θ
0
θ
cos θ
3π
2
0
5π
3
1
2
7π
4
11π
6
√1
2
√
3
2
2π
1
cos θ
π
−1
√
3
2
2π
3
− 12
7π
6
−
π
4
√1
2
3π
4
5π
4
− √12
π
3
1
2
5π
6
− √12
√
− 23
4π
3
− 21
π
6
θ
3
2
The sketch of the graph of f (θ) = cos θ in the interval [0, 2π] is given below.
y
1
π π π
6 4 3
π
2
π
3π
2
2π
θ
−1
The cosine function is also a periodic function with period 2π. The amplitude of the
cosine function is 1, the maximum value of the cosine function is 1, and the minimum
value of the cosine function is −1.
128
CHAPTER 6. TRIGONOMETRIC FUNCTIONS
Exercise.
1.
2.
3.
4.
5.
Prove
Prove
Prove
Prove
Prove
that
that
that
that
that
the
the
the
the
the
period of f (θ) = cos θ is 2π.
maximum value of f (θ) = cos θ is 1.
minimum value of f (θ) = cos θ is −1.
amplitude of f (θ) = cos θ is 1.
domain of f (θ) = cos θ is (−∞, ∞) and the range is [−1, 1].
The graph of the cosine function in the interval [0, 2π] is given below.
y
1
π
π
2
3π
2
2π
θ
−1
The following are a few important observation of the above graph.
1. The cosine function has zeros at π2 and at 3π
in [0, 2π].
2
2. The cosine function has the maximum value at 0 and at 2π in [0, 2π].
3. The cosine function has the minimum value at π in [0, 2π].
Exercise.
1. Prove that f (θ) = cos θ is symmetrical with respect to x = 0 in the interval [− π2 , π2 ].
y
1
α
− π2 −α
π
2
−1
2. Prove that f (θ) = cos θ is symmetrical with respect to x = π in the interval [ π2 , 3π
].
2
θ
6.2. COSINE FUNCTION
129
y
1
π
2
π−α
π+α
π
3π
2
θ
−1
Example. Identify the amplitude, the period, the phase shift, and sketch the graph of
f1 (θ) = 3 cos 3(θ + π3 ) over one period.
Answer. Let α = 3(θ + π3 ). Then θ =
α
cos α
α
3
0
1
0
π
2
0
π
− π3 .
cos 3(θ + π3 )
3 cos 3(θ + π3 )
− π3
1
3
π
6
− π6
0
0
−1
π
3
0
−1
−3
3π
2
0
π
2
π
6
0
0
2π
1
2π
3
π
3
1
3
θ=
y
3
− π3 − π6
−3
π
6
π
3
θ
α
3
α
3
−
π
3
130
CHAPTER 6. TRIGONOMETRIC FUNCTIONS
The amplitude of f1 is 3, the period is
6.3
2π
,
3
and the phase shift is − π3 .
Tangent Function
We define the tangent number of a given angle θ, written as tan θ as follows.
tan θ =
sin θ
cos θ
Since both sin θ and cos θ are unique numbers for the given θ, and if cos θ 6= 0, then tan θ
is a unique number for a given angle θ. Also, according to this definition, tan θ does not
do not exist.
exist, when cos θ = 0. For example, tan − π2 , tan π2 or tan 3π
2
We can visualize the number tan θ on the unit circle, for given angle θ in the domain of
the tangent function. First, recall the following theorems from high school.
The Slope of a Line Theorem. The slope of a line passing through the points
−y1
(x1 , y1 ) and (x2 , y2 ) is xy22 −x
.
1
The Tangent to a Circle Theorem. A line tangent to a circle is perpendicular to
the line passing through the point of tangency and the center of the circle.
Consider an angle 0 ≤ θ < π2 . Let ` be the line containing the terminal side of the
angle θ in the standard position. The coordinates of the point of intersection of ` and
the unit circle is (cos θ, sin θ). Also ` passes through (0, 0). Since we know coordinates of
two points on `, we can calculate the slope of the line according to the Slope of a Line
Theorem. That is, the slope of ` is tan θ. We can get another point on ` as follows. Draw
a line `1 tangent to the unit circle at (1, 0). Let P be the point of intersection of ` and
`1 . By the Tangent to a Circle Theorem, `1 ⊥ x-axis. Therefore, the x-coordinate of P
is 1. Suppose the y-coordinate is y0 . Then by using P (1, y0 ) and O(0, 0) to calculate the
slope of ` we get:
tan θ =
y0 − 0
.
1−0
6.3. TANGENT FUNCTION
131
That is, y0 = tan θ.
`1
P (1, tan θ)
(cos θ, sin θ)
θ
(1, 0)
`
In other words, the length of the line segment joining (1, 0) and P is tan θ.
`1
P
tan θ
θ
(1, 0)
`
Clearly, tan 0 = 0. We can see now that the tangent number of an angle θ increases as θ
varies from 0 to π2 and the tangent number increases without bounds as θ → π2 .
Now consider an angle π2 < θ ≤ π. For an angle θ in ( π2 , π) sin θ > 0 and cos θ < 0.
Therefore, the value of tan θ < 0 in the interval ( π2 , π). We can visualize the value of the
132
CHAPTER 6. TRIGONOMETRIC FUNCTIONS
number − tan θ, for a given θ in ( π2 , π] as a length of a line segment just as we did in the
interval [0, π2 ).
`1
P
− tan θ
θ
(−1, 0)
`
The value of − tan θ decreases as θ varies from π2 to π. The value of − tan θ is 0 when
θ = π. That means the value of tan θ increases in the interval ( π2 , π].
For an angle θ in (π, 3π
), sin θ < 0 and cos θ < 0. Therefore, the value of tan θ > 0 in the
2
3π
) as
interval [π, 2 ). We can visualize the value of the number tan θ, for a given θ in [π, 3π
2
a length of a line segment just as we did before.
`
θ
(−1, 0)
tan θ
P
`1
The value of tan θ increases as θ varies from π to 3π
. The values of tan θ increase without
2
bound when the values of θ get closer to 3π
, and tan 3π
does not exist.
2
2
For θ in ( 3π
, 2π), sin θ < 0 and cos θ > 0. Therefore, the value of tan θ < 0 in the interval
2
3π
, 2π] as a
( 2 , 2π). We can visualize the value of the number − tan θ, for a given θ in ( 3π
2
length of a line segment as before.
6.3. TANGENT FUNCTION
133
`
θ
(1, 0)
− tan θ
P
`1
The value of − tan θ decreases as θ varies from 3π
to 2π. Therefore, the values of tan θ
2
3π
increase as θ varies from 2 to 2π. The values of tan θ is 0 when θ = 2π.
We can calculate the tangent values of special angles using the definition. The tangent
values for special angles are given below. The abbreviation DNE stands for “Does Not
Exist”.
θ
tan θ
θ
0
0
π
2
π
6
√1
3
2π
3
1
√
3
π
4
π
3
tan θ
θ
DNE
√
− 3
π
0
7π
6
√1
3
3π
4
−1
5π
4
5π
6
− √13
1
√
3
4π
3
θ
tan θ
3π
2
5π
3
DNE
√
− 3
7π
4
−1
11π
6
− √13
2π
0
tan θ
Since tan θ is unique for any θ wherever tan θ is defined, f (θ) = tan θ is a function. The
domain of this function is all real numbers except where cos θ = 0.
The collection of all points (θ, tan θ) is called the graph of the function f (θ) = tan θ. We
can sketch the graph of f (θ) = tan θ by using all the information we have gathered about
tangent numbers for θ in the interval [0, 2π].
134
CHAPTER 6. TRIGONOMETRIC FUNCTIONS
y
2
1
πππ
6 4 3
π
π
2
2π
3π
2
θ
−1
−2
There are vertical asymptotes to the tangent function at π2 and at 3π
, by the definition
2
π
of a vertical asymptote. We will include the vertical asymptotes x = 2 and x = 3π
with
2
the graph of the tangent function in the interval [0, 2π] as shown below.
y
2
1
−1
πππ π
643 2
π
3π
2
2π
θ
−2
If θ =
nπ
,
2
for any integer n, then sin θ = ±1 and cos θ = 0. Therefore, by definition, tan θ
6.3. TANGENT FUNCTION
135
does not exist for such θ. For any other angle θ, the tangent function is defined, since
cos θ 6= 0. That is, the domain of f (θ) = tan θ is all real numbers except the points where
θ = nπ
, for some integer n.
2
We are going to prove that the tangent function is periodic. We need several “little theorems” first. The word used to describe any little theorem that is needed in a subsequent
theorem is “lemma”.
We say a graph of an equation is symmetric with respect to the origin if (−x, −y) is a
point on the graph whenever (x, y) is a point on the graph.
Lemma (Lemma 1). The unit circle is symmetric with respect to the origin.
(x, y)
(−x, −y)
Proof. The equation of the unit circle is x2 + y 2 = 1. Let (x1 , y1 ) be an arbitrary point
on the unit circle. Then x21 + y12 = 1. We want to show that (−x1 , −y1 ) is also a point on
the unit circle. This is true because (−x1 )2 + (−y1 )2 = x21 + y12 = 1.
Lemma (Lemma 2). Let (x1 , y1 ) be an arbitrary point in the xy-coordinate system.
Then the line passing through the points (x1 , y1 ) and (−x, − y1 ) passes through the
origin.
136
CHAPTER 6. TRIGONOMETRIC FUNCTIONS
(x, y)
(−x, −y)
Proof. If both x1 and y1 are 0, then (x1 , y1 ) = (−x, − y1 ) = (0, 0). Any line containing
(0, 0) passes through the origin.
If x1 = 0 and y1 6= 0, then (0, y1 ) and (0, −y1 ) lies on the horizontal line y = 0, and this
horizontal line passes through the origin.
If x1 6= 0 and y1 = 0, then (x1 , 0) and (−x1 , 0) lies on the vertical line x = 0, and this
vertical line passes through the origin.
If both x1 and y1 are not 0, then the slope of the line ` passing through (x1 , y1 ) and
(−x, − y1 ) is xy11 . Since ` passes through (x1 , y1 ), the equation of ` is y − y1 = xy11 (x − x1 ).
That is, the equation of ` is y = xy11 x. Since (0, 0) is a solution of this equation, ` passes
through the origin.
Theorem. The function f (θ) = tan θ is periodic.
Proof. Let θ be an arbitrary angle in the domain of the tangent function. First assume
that θ lies in any one of the four quadrants. We know that P (cos θ, sin θ) is a point on the
unit circle. Then by the Lemma 1, Q(− cos θ, − sin θ) is also a point on the unit circle.
By the Lemma 2, The line P Q passes through the origin. Therefore, − cos θ = cos(π + θ)
and − sin θ = sin(π + θ). By definition,
tan θ =
sin θ
cos θ
6.3. TANGENT FUNCTION
137
− sin θ
− cos θ
sin(π + θ)
=
cos(π + θ)
=
= tan(π + θ)
Now suppose that the terminal side of θ lies on the x-axis. Then θ = nπ, for some integer
n, and sin θ = 0 and cos θ = ±1. By definition, tan nπ = 0 for any integer n. In particular,
tan(n + 1)π = 0, since n + 1 is an integer. Therefore, tan θ = tan(π + θ).
Since we have chosen θ to be an arbitrary angle in the domain of f in all cases, the
function f (θ) = tan θ is periodic.
Theorem. The period of f (θ) = tan θ is π.
The following is the graph of the tangent function in the interval [−2π, 2π].
y
−2π
− 3π
2
−π
− π2
π
2
π
3π
2
2π
θ
138
CHAPTER 6. TRIGONOMETRIC FUNCTIONS
Exercise. Show that the tangent function has no amplitude.
Exercise. Consider the graph of f (θ) = tan θ; − π2 < θ < π2 as the graph of the tangent
function over one period. Sketch the graph of f1 (θ) = 2 tan 3 θ − π4 over one period and
identify the amplitude, period, and the phase shift.
6.4
Cosecant Function
At this point we recognize that an angle θ in radians is just a number. Therefore, we
will replace θ with x and sketch the graphs of trigonometric functions in the familiar
xy-coordinate system rather than the θy-coordinate system that we have been using so
far.
We define csc x, pronounced “cosecant x” as
csc x =
1
for any real number x, where sin x 6= 0.
sin x
Since sin x is unique for any real number x, csc x is also unique for any x where csc x is
defined. Therefore, f (x) = csc x is a function and the domain of f is all real numbers
except where sin x = 0.
Since sin x = 0, when x = nπ, for any integer n, the cosecant function f (x) = csc x does
not exist for x = nπ. Let us look at f (x) = csc x over [0, 2π]. We will find the cosecant
numbers of special angles first.
x
0
π
6
π
4
π
3
sin x
0
1
2
√1
2
√
3
2
csc x
x
DNE
π
2
sin x
1
√
3
2
2
√
2
2π
3
3π
4
√1
2
√2
3
5π
6
1
2
csc x
1
√2
3
√
2
2
x
π
sin x
0
7π
6
− 12
5π
4
− √12
4π
3
√
− 3
2
x
sin x
csc x
3π
2
−1
−1
csc x
DNE
−2
√
− 2
− √23
√
3
2
5π
3
−
7π
4
− √12
− √23
√
− 2
11π
6
− 21
−2
2π
0
DNE
6.4. COSECANT FUNCTION
139
Exercise.
1.
2.
3.
4.
Show
Show
Show
Show
that
that
that
that
as
as
as
as
x → 0+ , csc x → ∞.
x → π − , csc x → ∞.
x → π + , csc x → −∞.
x → 2π − , csc x → −∞.
According to the results of the above exercise, x = 0, x = π and x = 2π are asymptotes
of the cosecant function. With the collected information above, we can sketch the graph
of f (x) = csc x over the interval [0, 2π].
y
πππ
6 4 3
π
2
π
x
3π
2
2π
Theorem. The function f (x) = csc x is periodic, with period 2π.
Exercise. Prove the above theorem.
Exercise. Show that the function f (x) = csc x has no amplitude.
140
CHAPTER 6. TRIGONOMETRIC FUNCTIONS
6.5
Secant Function
We define sec x, pronounced “secant x” as
sec x =
1
for any real number x, where cos x 6= 0.
cos x
Since cos x is unique for any real number x, sec x is also unique for any x where sec x is
defined. Therefore, f (x) = sec x is a function, and the domain of f is all real numbers
except where cos x = 0.
Since cos x = 0, when x = nπ
, for any integer n 6= 0, the secant function f (x) = sec x
2
does not exist at those points. Let us look at f (x) = sec x over [0, 2π]. The following are
secant numbers of special angles.
x
cos x
0
1
√
3
2
π
6
π
4
√1
2
π
3
1
2
sec x
x
1
π
2
√2
3
√
2
0
2π
3
− 12
3π
4
− √12
√
− 23
5π
6
2
cos x
sec x
DNE
x
π
cos x
−1
√
3
2
x
cos x
sec x
3π
2
0
DNE
5π
3
1
2
7π
4
11π
6
√1
2
√
3
2
2
√
2
2π
1
sec x
−1
−2
√
− 2
7π
6
− √23
−
5π
4
− √12
√
− 2
− √23
4π
3
− 12
−2
√2
3
1
Exercise.
1.
2.
3.
4.
Show
Show
Show
Show
that
that
that
that
as
as
as
as
x→
x→
x→
x→
π−
,
2
π+
,
2
π−
,
3
π+
,
3
sec x → ∞.
csc x → −∞.
csc x → −∞.
csc x → −∞.
According to the results of the above exercise, x = π2 and x = 3π
are asymptotes of
2
the secant function. With the collected information above, we can sketch the graph of
f (x) = sec x over the interval [0, 2π].
6.5. SECANT FUNCTION
141
y
π π π
6 4 3
π
2
π
x
3π
2
2π
Theorem. The function f (x) = sec x is periodic, with period 2π.
Exercise. Prove the above theorem.
Exercise. Show that the function f (x) = sec x has no amplitude.
142
CHAPTER 6. TRIGONOMETRIC FUNCTIONS
6.6
Cotangent Function
We define cot x, pronounced “cotangent x” as
cot x =
1
for any real number x, where tan x 6= 0.
tan x
Since tan x is unique for any real number x, cot x is also unique for any x where cot x is
defined.
Theorem. cot x =
cos x
, for any real number x, where sin x 6= 0.
sin x
Then f (x) = cot x is a function and the domain of f is all real numbers except where
sin x = 0.
Since sin x = 0, when x = nπ, for any integer n, the secant function f (x) = cot x does not
exist at those points. Let us look at f (x) = cot x over [0, 2π]. The following are cotangent
numbers of special angles.
x
cos x
sin x
cot x
x
cos x
sin x
cot x
x
cos x
sin x
cot x
0
1
0
DNE
√
3
π
2
0
1
0
π
−1
0
2π
3
− 12
3
2
− √13
7π
6
−
− 12
DNE
√
3
1
3π
4
− √12
√1
2
5π
4
− √12
− √12
1
√1
3
5π
6
−
−1
√
− 3
4π
3
− 12
−
√
3
2
1
2
π
4
√1
2
π
3
1
2
√1
2
√
3
2
π
6
x
cos x
sin x
cot x
3π
2
0
−1
0
5π
3
1
2
7π
4
√
3
2
− √13
− √12
11π
6
√1
2
√
3
2
− 12
−1
√
− 3
2π
1
0
DNE
−
√
3
2
√
1
2
√
3
2
√
3
2
√1
3
6.6. COTANGENT FUNCTION
143
Exercise.
1.
2.
3.
4.
Show
Show
Show
Show
that
that
that
that
as
as
as
as
x → 0+ , cot x → ∞.
x → π − , csc x → −∞.
x → π + , csc x → ∞.
x → 2π − , csc x → −∞.
According to the results of the above exercise, x = 0, x = π and x = 2π are asymptotes
of the cotangent function. With the collected information above, we can sketch the graph
of f (x) = cot x over the interval [0, 2π].
y
πππ
6 4 3
π
2
π
3π
2
2π
θ
Theorem. The function f (x) = cot x is periodic with period π.
Exercise. Prove the above theorem.
Exercise. Show that the function f (x) = cot x has no amplitude.
Chapter 7
Inverse Trigonometric Functions
Consider a function f of x. For each number x in the domain of f , the function f produces
a unique number f (x). We can indicate this using the following notation.
f : x → f (x)
If the number x is also unique, that is, no two numbers x1 and x2 produce f (x1 ) = f (x2 ),
then we can find a function, say g, to reverse the process of f . That is, for each number
f (x), g produces a unique number x.
g : f (x) → x
Not all functions behave this way. For example, consider f1 (x) = x2 . Then
f1 : 2 → f (2) = 4
and
f1 : −2 → f (−2) = 4
Therefore, we cannot find a function g to reverse the process of f1 . If we restrict the
domain of f1 to [0, ∞), then we can reverse the process. Let f2 = x2 ; x ≥ 0. Then there
is a function g2 so that
g2 : f2 (x) → x
We say a function with the property “for each number x there is a unique number f (x)
and for each f (x) there is a unique number x” is “one-to-one” or 1-1.
The following is a theorem that you may have learned in high school.
145
146
CHAPTER 7. INVERSE TRIGONOMETRIC FUNCTIONS
Theorem. If the graph of a given function f satisfies both the vertical line test and
the horizontal line test, then f is 1-1.
In a nutshell, the vertical line test is designed to see if there is a unique f (x) for a given
x in the domain of f , and the horizontal line test is designed to see if there is a unique x
in the domain of f for a given f (x) in the range of f .
If a function f is 1-1, then there is a function g so that g : f (x) → x. We usually use the
notation f −1 , pronounced “eff inverse” for such a function. We call such a function “the
inverse function of f ”. The following is the definition of a inverse function.
We say f and f −1 are inverse functions of each other if both of the following two conditions
hold.
1. For each x in the domain of f , f −1 (f (x)) = x.
2. For each x in the domain of f −1 , f (f −1 (x)) = x.
ab-ba Theorem. (a, b) is a point on the graph of f if and only if (b, a) is a point on
the graph of f −1 .
Proof. Suppose (a, b) is a point on the graph of f . Then b = f (a). Since a is on the
domain of f , f −1 (f (a)) = a, by definition. That is, f −1 (b) = a. That is, (b, a) is a point
on the graph of f −1 .
Now suppose (a, b) is a point on the graph of f −1 . Then b = f −1 (a). Since a is on the
domain of f −1 , f (f −1 (a)) = a, by definition. That is, f (b) = a. That is, (b, a) is a point
on the graph of f .
You may have learned the following definition in high school geometry. A point P (a, b)
is called the mirror image of the point Q(c, d) across a line `, and vice versa, if ` is the
perpendicular bisector of the segment P Q.
147
P
Q
`
Let G1 be the graph of a function f1 and let G2 be the graph of a function f2 . We say G1
is the mirror image of G2 across a line ` and vice versa, if each point on G1 is a mirror
image of a point on G2 across ` and each point on G2 is a mirror image of a point on G1
across `.
Reflection Theorem. Let G1 be the graph of a 1-1 function f and let G2 be the
graph of f −1 . Then G2 is the mirror image of G1 across the line ` whose equation is
y = x, and vice versa.
Proof. We will show that G2 is the mirror image of G1 across `. Let P (a, b) be an arbitrary
point on G1 . Then by the ab-ba Theorem, Q(b, a) is on G2 . Let `1 be the line LP Q . Then
a−b
the slope of `1 is b−a
= −1. The slope of ` is 1. Therefore, `1 is perpendicular to `.
a+b
The midpoint of P Q is R a+b
,
. Clearly, R is on `. Therefore, ` is the perpendicular
2
2
bisector of the segment P Q. Since P is arbitrary, G2 is the mirror image of G1 across `.
The proof of the statement “G1 is the mirror image of G2 across `” is similar.
The graph of the equation y = x is known as the diagonal of the xy-plane or simply the
diagonal.
148
7.1
CHAPTER 7. INVERSE TRIGONOMETRIC FUNCTIONS
Inverse Sine Function
Let us get the mirror image of the graph of the sine function across the diagonal.
y
1
− π2
−1
−2π − 3π −π
2
π
2
π
x
3π
2
2π
The blue curve in the above figure is the reflection of the graph of the sine function across
the diagonal. By using vertical line test, you can clearly see that this graph is not a graph
of a function. Therefore, the blue curve cannot be the graph of the inverse sine function.
The reason why we cannot use the Reflection Theorem here is that the sine function is
not 1-1.
The largest value of the sine function is 1 and the smallest value of the sine function is
−1. You get all possible values of the sine function even if we restrict the domain of the
sine function to the interval − π2 , π2 .
The following is the graph of the restricted sine function f (x) = sin x; − π2 ≤ x ≤ π2 .
y
1
− π2
π
2
x
−1
Notice that the restricted sine function is 1-1. Therefore, there is an inverse function for
7.2. INVERSE COSINE FUNCTION
149
the restricted sine function. We will use the usual notation reserved for inverse functions
to define the inverse sine function.
π
π
sin−1 (sin(x)) = x, if − ≤ x ≤ , and
2
2
sin(sin−1 (x)) = x, if − 1 ≤ x ≤ 1.
The blue curve in the following figure is the graph of f (x) = sin−1 x.
y
π
2
1
− π2
−1
1
π
2
x
−1
− π2
7.2
Inverse Cosine Function
Let us get the mirror image of the graph of the cosine function across the diagonal.
150
CHAPTER 7. INVERSE TRIGONOMETRIC FUNCTIONS
y
1
−2π − 3π
2
−π
− π2
−1
π
π
2
x
3π
2
2π
The blue curve in the above figure is the reflection of the graph of the cosine function
across the diagonal. By using vertical line test, you can clearly see that this graph is not
a graph of a function. Therefore, the blue curve cannot be the graph of the inverse cosine
function.
We can get all possible values of the sine function even if we restrict the domain of the
cosine function to the interval [0, π].
The following is the graph of the restricted cosine function f (x) = cos x; 0 ≤ x ≤ π.
y
1
π
2
π
x
−1
Notice that the restricted cosine function is 1-1. Therefore, there is an inverse function for
the restricted sine function. We will use the usual notation reserved for inverse functions
to define the inverse cosine function.
cos−1 (cos(x)) = x, if 0 ≤ x ≤ π, and
7.3. INVERSE TANGENT FUNCTION
151
cos(cos−1 (x)) = x, if − 1 ≤ x ≤ 1.
The blue curve in the following figure is the graph of f (x) = cos−1 x.
y
π
π
2
1
−1
1
π
2
π
x
−1
7.3
Inverse Tangent Function
Let us get the mirror image of the graph of the tangent function across the diagonal.
152
CHAPTER 7. INVERSE TRIGONOMETRIC FUNCTIONS
y
−2π
− 3π
2
−π
− π2
π
2
π
x
3π
2
2π
The blue curves in the above figure are the reflection of the graph of the tangent function
across the diagonal. By using the vertical line test, you can clearly see that this graph is
not a graph of a function. Therefore, the blue curves cannot be the graph of the inverse
tangent function.
You get all possible values of the tangent function even if we restrict the domain of the
tangent function to the interval − π2 , π2 .
The following is the graph of the restricted tangent function f (x) = tan x; − π2 < x < π2 .
7.3. INVERSE TANGENT FUNCTION
153
y
π
2
− π2
π
2
x
− π2
Notice that the restricted tangent function is 1-1. Therefore, there is an inverse function
for the restricted tangent function. We will use the usual notation reserved for inverse
functions to define the inverse tangent function.
tan−1 (tan(x)) = x, if −
π
π
< x < , and
2
2
tan(tan−1 (x)) = x.
The blue curve in the following figure is the graph of f (x) = tan−1 x.
154
CHAPTER 7. INVERSE TRIGONOMETRIC FUNCTIONS
y
π
2
− π2
π
2
− π2
We can similarly define inverse functions for the remaining three trigonometric functions
by appropriately restricting the domain of each function. The following is the summary.
Filling in the details is left as an exercise.
x
7.4. INVERSE COSECANT FUNCTION
7.4
155
Inverse Cosecant Function
h π πi
csc−1 (csc(x)) = x, if x is in − , 0 ∪ 0,
and
2
2
csc(csc−1 (x)) = x, if x is in(−∞, −1] ∪ [1, ∞).
The blue curve in the following figure is the graph of f (x) = csc−1 x.
y
π
2
1
− π2 −1
1
−1
− π2
π
2
x
156
7.5
CHAPTER 7. INVERSE TRIGONOMETRIC FUNCTIONS
Inverse Secant Function
π πi
sec−1 (sec(x)) = x, if x is in − , 0 ∪ 0,
and
2
2
sec(sec−1 (x)) = x, if x is in(−∞, −1] ∪ [1, ∞).
The blue curve in the following figure is the graph of f (x) = sec−1 x.
y
π
1
−1
1
−1
π
x
7.6. INVERSE COTANGENT FUNCTION
7.6
157
Inverse Cotangent Function
π πi
and
cot−1 (cot(x)) = x, if x is in − , 0 ∪ 0,
2
2
cot(cot−1 (x)) = x.
The blue curve in the following figure is the graph of f (x) = cot−1 x.
y
π
2
− π2
π
2
− π2
x
158
CHAPTER 7. INVERSE TRIGONOMETRIC FUNCTIONS
Example. Find sin−1 sin 5π
, if possible.
6
Solution. By the definition of the inverse sine function, sin−1 (sin(x)) = x, if x is in
− π2 , π2 . Clearly, 5π
is not in − π2 , π2 . Does that mean sin−1 sin 5π
doesn’t exist? No6
6
5π
tice that sin 6 is defined and the sine function is symmetric with respect to the line x = π2 .
y
1
− π2
π
6
−1
π
2
x
5π
6
Therefore, sin 5π
= sin π6 .
6
Then sin−1 sin 5π
= sin−1 sin π6 = π6 , by definition of the inverse sine function.
6
Example. Find sin sin−1 5π
, if possible.
6
−1 5π
is
greater
than
1.
Therefore,
sin
Solution. The number 5π
does not exist, by
6
6
−1 5π
definition. That is, sin sin
does not exist.
6
Example. Find sin sin−1 π6 , if possible.
π
−1 π
exists
and
sin
sin
= 6 , by
Solution. Clearly, −1 < π6 < 1. Therefore, sin−1 5π
6
6
definition.
Chapter 8
Basic Trigonometric Equations
When we looked at quadratic equations in a real number x, we realized that we could solve
any quadratic equation by completing the square. This observation leads to deriving the
quadratic formula for real numbers. In a similar fashion, by knowing that trigonometric
functions are periodic and by keeping in mind some symmetries that we observed with
trigonometric functions, we should be able to find the solutions to trigonometric equations
of the form given below.
1. sin x = a
2. cos x = a
3. tan x = a
where, a is a real number.
Except for one special case, we can solve equations of the form csc x = a, sec x = a
and cot x = a, for a real number a, by writing those equations in an equivalent form as
sin x = a1 , cos x = a1 and tan x = a1 . The special case arises when cot x = 0, and we will
handle this special case separately.
8.1
Solving the Sine Equation
Consider the equation sin x = a, where a is a real number. First notice that if a > 1 or
a < −1, then this equation has no solutions, as −1 ≤ sin x ≤ 1, for all real numbers x.
Therefore, we want to find the solutions of
sin x = a, where − 1 ≤ a ≤ 1.
159
160
CHAPTER 8. BASIC TRIGONOMETRIC EQUATIONS
First notice that there are infinitely many solutions to this equation. In the following
figure . . . , s−3 , s−2 , s−1 , s1 , s2 , s3 , s4 , . . . are solutions to the above equation for some real
number a, where 0 < a < 1.
y
1
a
s−3
s−2
s−1
s1
s2
s3
s4
x
−1
Consider the case − π2 ≤ x ≤
sin−1 (sin x) = x. Therefore,
sin x = a
=⇒ sin−1 (sin x) = sin−1 a
=⇒ x = sin−1 a
π
.
2
Then by the definition of the inverse sine function,
That is, the solution titled s1 in the above figure is sin−1 a.
y
1
a
s−2
s−1
−1
sin−1 a
s−3
s2
s3
s4
x
By using the symmetries that we have discovered in the graph of the sine function, we
know that s2 = π − sin−1 a. Since the portion of the graph on the interval [2π, 3π] is
congruent to the portion of the graph on the interval [0, π] (why?), s3 = 2π + sin−1 a and
s4 = 3π − sin−1 a. By the same argument, s−1 = −π − sin−1 a, s−2 = −2π + sin−1 a,
and s−3 = −3π − sin−1 a, etc. Then the following are the solutions of the trigonometric
equation sin x = a when 0 < a < 1.
. . . , (−3π−sin−1 a), (−2π+sin−1 a), (−π−sin−1 a), (sin−1 a), (π−sin−1 a), (2π+sin−1 a), . . .
Exercise. Show that the solutions of sin x = a, where −1 < a < 0 are:
. . . , (−π−sin−1 a), (−2π+sin−1 a), (π−sin−1 a), (sin−1 a), (3π−sin−1 a), (2π+sin−1 a), . . .
Exercise. Show that the solutions of sin x = a, where a = 0 are:
. . . , −3π, −2π, −π, 0, π, 2π, 3π, . . .
8.1. SOLVING THE SINE EQUATION
161
The following theorem captures everything we have found so far.
General Solution to the Sine Equation Theorem.
Suppose sin x = a is a given equation, where a is a real number.
1. If a > 1 or a < −1, then the equation has no solutions.
2. If −1 ≤ a ≤ 1, then the general solution of the equation is nπ + (−1)n sin−1 a,
where n is any integer.
Example. Find the general solution of sin x = − 21 . Find the solutions of sin x = − 21 in
the interval [−4π, 4π].
Solution. By the General Solution to the Sine Equation Theorem, the solutions are:
1
n
−1
, for any integer n.
x = nπ + (−1) sin
−
2
Since sin − π6 = − 21 , by the definition of the inverse sine function, sin−1 − 12 = sin−1 (sin − π6 ) =
− π6 . Therefore, the general solution to the given equation is:
π
x = nπ − (−1)n , for any integer n.
6
When n = 0, x = − π6 . This solution is more than −4π. We keep it.
When n = 1, x = π + π6 = 7π
. This solution is less than 4π. We keep it.
6
π
11π
When n = 2, x = 2π − 6 = 6 . This solution is less than 4π. We keep it.
When n = 3, x = 3π + π6 = 19π
. This solution is less than 4π. We keep it.
6
π
23π
When n = 4, x = 4π − 6 = 6 . This solution is less than 4π. We keep it.
When n = 5, x = 5π + π6 . This solution is more than 4π, and any larger value of n
produces a solution larger than 4π. Therefore, we will not keep solutions for any n more
than 4.
Now let us try negative integers.
When n = −1, x = −π + π6 = − 5π
. This solution is more than −4π. We keep it.
6
π
13π
When n = −2, x = −2π − 6 = − 6 . This solution is more than −4π. We keep it.
. This solution is more than −4π. We keep it.
When n = −3, x = −3π + π6 = − 17π
6
π
When n = −4, x = −4π − 6 . This solution is less than −4π, and any smaller value of
162
CHAPTER 8. BASIC TRIGONOMETRIC EQUATIONS
n produces a solution less than −4π. Therefore, we will not keep solutions for any n less
than −3.
Therefore, the solutions of the equation sin x = − 12 in the interval [−4π, 4π] are:
−
17π 13π 5π π 7π 11π 19π 23π
,−
,− ,− , ,
,
,
6
6
6
6 6 6
6
6
The following figure shows the solutions to sin x = − 21 in the interval [−4π, 4π] graphically.
y
−17π
6
−13π
6
−5π
6
−π
6
7π
6
11π
6
19π
6
23π
6
x
√
√
Example. Find the general solution of sin 3x =
the interval [−π, π].
3
.
2
Find the solutions of sin 3x =
3
2
in
Solution. By the General Solution to the Sine Equation Theorem, the solutions are:
√ !
3
3x = nπ + (−1)n sin−1
, for any integer n.
2
π
3
Since sin
=
π
. Therefore,
3
√
3
,
2
−1
by the definition of the inverse sine function, sin
√ 3
2
= sin−1 (sin
π
3
π
3x = nπ + (−1)n , for any integer n.
3
By multiplying both sides by 31 , we get the general solution to the given equation.
1
π
x = nπ + (−1)n , for any integer n.
3
9
When n = 0, x = π9 . This solution is less than π. We keep it.
When n = 1, x = π3 − π9 = 2π
. This solution is less than π. We keep it.
9
2π
π
7π
When n = 2, x = 3 + 9 = 9 . This solution is less than π. We keep it.
When n = 3, x = π − π9 = 8π
. This solution is less than π. We keep it.
9
π
13π
4π
When n = 4, x = 3 + 9 = 9 . This solution is more than π, and any larger value of n
produces a solution larger than π. Therefore, we will not keep solutions for any n more
than 4.
Now let us try negative integers.
When n = −1, − π3 − π9 = − 4π
. This solution is more than −π. We keep it.
9
)=
8.2. SOLVING THE COSINE EQUATION
163
When n = −2, − 2π
+ π9 = − 5π
. This solution is more than −π. We keep it.
3
9
π
. This solution is less than −π, and any smaller value
When n = −3, x = −π − 9 = − 10π
6
of n produces a solution less than −π. Therefore, we will not keep solutions for any n
less than −3.
√
Therefore, the solutions of the equation sin 3x =
−
8.2
3
2
in the interval [−π, π] are:
5π 4π π 2π 7π 8π
,− , , , ,
9
9 9 9 9 9
Solving the Cosine Equation
Consider the equation cos x = a, where a is a real number. First notice that if a > 1 or
a < −1, then this equation has no solutions, as −1 ≤ cos x ≤ 1, for all real numbers x.
Therefore, we want to find the solutions of
cos x = a, where − 1 ≤ a ≤ 1.
Again notice that there are infinitely many solutions to this equation. In the following
figure . . . , s−3 , s−2 , s−1 , s1 , s2 , s3 , s4 , . . . are solutions to the above equation for some real
number a, where 0 < a < 1.
y
1
a
s−3
s−2
s−1
s1
s2
s3
x
−1
Consider the case 0 ≤ x ≤ π. Then by the definition of the inverse cosine function,
cos−1 (cos x) = x. Therefore,
cos x = a
=⇒ cos−1 (cos x) = cos−1 a
=⇒ x = cos−1 a
That is, the solution titled s1 in the above figure is cos−1 a.
y
1
a
s−2
s−1
−1
cos−1 a
s−3
s2
s3
x
164
CHAPTER 8. BASIC TRIGONOMETRIC EQUATIONS
By using the symmetries that we have discovered in the graph in the cosine function,
, 5π
] is
we know that s−1 = − cos−1 a. Since the portion of the graph on the interval [ 3π
2
2
π π
congruent to the portion of the graph on the interval [− 2 , 2 ] (why?), s2 = 2π−cos−1 a and
s3 = 2π + cos−1 a. By the same argument, s−2 = −2π + cos−1 a and s−3 = −2π − cos−1 a,
etc. Then the following are the solutions of the trigonometric equation cos x = a when
0 < a < 1 are:
. . . , (−2π−cos−1 a), (−2π+cos−1 a), (− cos−1 a), (cos−1 a), (2π−cos−1 a), (2π+cos−1 a), . . .
Exercise. Show that the solutions of cos x = a, where −1 < a < 0.
. . . , (−2π−cos−1 a), (−2π+cos−1 a), (− cos−1 a), (cos−1 a), (2π−cos−1 a), (2π+cos−1 a), . . .
Exercise. Show that the solutions of cos x = a, where a = 0 are:
...,−
π 3π 5π
5π 3π π
, − , − , 0, , , , . . .
2
2
2
2 2 2
The following theorem captures everything we have found so far.
General Solution to the Cosine Equation Theorem.
Suppose cos x = a is a given equation, where a is a real number.
1. If a > 1 or a < −1, then the equation has no solutions.
2. If −1 ≤ a ≤ 1, then the general solution of the equation is 2nπ ± cos−1 a, where
n is any integer.
Example. Find the general solution of cos x = − 21 . Find the solutions of cos x = − 12 in
the interval [−4π, 4π].
Solution. By the General Solution to the Cosine Equation Theorem, the solutions are:
1
−1
x = 2nπ ± cos
−
, for any integer n.
2
Since cos 2π
= − 12 , by the definition of the inverse sine function, cos−1 − 21 = cos−1 (cos
3
2π
. Therefore, the general solution the given equation is:
3
x = 2nπ ±
2π
, for any integer n.
3
2π
3
)=
8.3. SOLVING THE TANGENT EQUATION
165
When n = 0, x = − 2π
or x = 2π
. Both answers are in the interval [−4π, 4π] so we keep
3
3
both of them.
When n = 1, x = 2π − 2π
= 4π
or x = 2π + 2π
= 8π
. Both answers are in the interval
3
3
3
3
[−4π, 4π] so we keep both of them.
= 10π
or x = 4π + 2π
. We keep the first solution but discard
When n = 2, x = 4π − 2π
3
3
3
the second solution, as it is more than 4π.
When n = 3, x = 6π − 2π
or x = 6π + 2π
. Both of these solutions are more than 4π.
3
3
Therefore, we will not keep solutions for any n more than 3.
Now let us try negative integers.
= − 8π
or x = −2π + 2π
= − 4π
. Both answers are in the
When n = −1, x = −2π − 2π
3
3
3
3
interval [−4π, 4π] so we keep both of them.
or x = −4π + 2π
= − 10π
. We keep the second solution but
When n = −2, x = −4π − 2π
3
3
3
discard the first solution, as it is less than −4π.
When n = −3, x = −6π − 2π
or x = −6π + 2π
. Both of these solutions are less than
3
3
−4π. Therefore, we will not keep solutions for any n less than −3.
The solutions of the equation cos x = − 12 in the interval [−4π, 4π] are:
−
10π 8π 4π 2π 2π 4π 8π 10π
,− ,− ,− , , , ,
3
3
3
3 3 3 3 63
The following figure shows the solutions to cos x = − 21 in the interval [−4π, 4π] graphically.
y
−10π
3
8.3
−8π
3
−4π
3
−2π
3
2π
3
4π
3
8π
3
10π
3
x
Solving the Tangent Equation
Consider the equation tan x = a, where a is a real number.
Again notice that there are infinitely many solutions to this equation. In the following
figure . . . , s−3 , s−2 , s−1 , s1 , s2 , s3 , s4 , . . . are solutions to the above equation for some real
number a.
166
CHAPTER 8. BASIC TRIGONOMETRIC EQUATIONS
y
a
s−3
s−2
s−1
Consider the case − π2 < x <
tan−1 (tan x) = x. Therefore,
tan x = a
=⇒ tan−1 (tan x) = tan−1 a
=⇒ x = tan−1 a
π
.
2
s1
s2
s3
x
By the definition of the inverse tangent function,
That is, the solution titled s1 in the above figure is tan−1 a.
8.3. SOLVING THE TANGENT EQUATION
167
y
a
s−2
s−1
tan−1 a
s−3
s2
s3
x
By using the symmetries that we have discovered in the graph of the tangent function,
we know that s1 = π + tan−1 a. Since the portion of the graph on the interval ( 3π
, 5π
)
2
2
π π
−1
is congruent to the portion of the graph on the interval (− 2 , 2 ), s2 = 2π + tan a and
s3 = 3π + tan−1 a. By the same argument, s−1 = −π + tan−1 a and s−2 = −2π + tan−1 a,
etc. Then the following are the solutions of the trigonometric equation tan x = a when
a > 0 are:
. . . , (−3π+tan−1 a), (−2π+tan−1 a), (π−tan−1 a), (tan−1 a), (π+tan−1 a), (2π+tan−1 a), . . .
Exercise. Show that the solutions of cos x = a, where a < 0 are:
. . . , (−3π+tan−1 a), (−2π+tan−1 a), (π−tan−1 a), (tan−1 a), (π+tan−1 a), (2π+tan−1 a), . . .
Exercise. Show that the solutions of tan x = a, where a = 0 are:
. . . , −3π, −2π, −π, 0, π, 2π, 3π, . . .
The following theorem captures everything we have found so far.
168
CHAPTER 8. BASIC TRIGONOMETRIC EQUATIONS
General Solution to the Tangent Equation Theorem.
Suppose tan x = a is a given equation, where a is a real number.
Then the general solution of the equation is nπ + tan−1 a, where n is any integer.
Example. Find the general solution of tan x = −1. Find the solutions of tan x = −1 in
the interval [−2π, 2π].
Solution. By the General Solution to the Tangent Equation Theorem, the solutions are:
x = nπ + tan−1 (−1) , for any integer n.
Since tan − π4 = −1, by the definition of the inverse sine function, tan−1 (−1) = tan−1 (tan − π4 ) =
− π4 . Therefore, the general solution the given equation is:
x = nπ −
π
, for any integer n.
4
When n = 0, x = − π4 . This solution is in the interval [−2π, 2π] so we keep it.
When n = 1, x = π − π4 = 3π
. This solution is in the interval [−2π, 2π] so we keep it.
4
π
7π
When n = 2, x = 2π − 4 = 4 . This solution is in the interval [−2π, 2π] so we keep it.
When n = 3, x = 3π − π4 or x = 2π + 3π
. This solution is more than 2π. Therefore, we
4
will not keep solutions for any n more than 2.
Now let us try negative integers.
When n = −1, x = −π − π4 = − 5π
. This solution is in the interval [−2π, 2π] so we keep
4
it.
When n = −2, x = −2π − π4 . This solution is less than 2π. Therefore, we will not keep
solutions for any n less than 1.
The solutions of the equation tan x = −1 in the interval [−2π, 2π] are:
−
5π π 3π 7π
,− , ,
4
4 4 4
The following figure shows the solutions to tan x = −1 in the interval [−2π, 2π] graphically.
8.3. SOLVING THE TANGENT EQUATION
169
y
−5π
4
−π
4
3π
4
7π
4
x
a
Now we will look at the special case mentioned at the beginning of this section. That
is how to solve the cot x = 0. In the domain of the inverse cotangent function, that is,
in the intervals (− π2 , 0) ∪ (0, π2 ], cot x = 0 when x = π2 . Therefore, cot−1 (0) = π2 , by
the definition of the inverse cotangent function. You should be able to easily prove the
following theorem now.
Theorem. The general solution to the equation cot x = 0 is nπ + π2 , for any integer
n.
Chapter 9
Applications: Solving a Triangle
In this chapter we will use the degree as the unit for the measure of an angle. We will also
use the following conventions throughout this section. Consider a given triangle ABC.
What we mean by this is that the vertices of the triangle are identified by the letters A,
B, and C. The angle at the vertex A is identified as α, the angle at vertex B is identified
as β, and the angle at the vertex C is identified as γ. The side facing the angle α is
identified as a, the side facing the angle β is identified as b, and the side facing the angle
γ is identified as c.
A
α
b
c
γ
B
β
C
a
We will refer to a triangle with angles and sides identified according to the above conventions as a triangle with standard notations.
The phrase“solving a triangle” means finding all six quantities; namely, the measures of
angles α, β, and γ, and the measures of the sides a, b, and c. We will loosely use the
names of the angles for angle measures as well. That is, it is understood that by saying
“α is 60 degrees” we really mean“the angle α has a measure of 60 degrees”. We will also
171
172
CHAPTER 9. APPLICATIONS: SOLVING A TRIANGLE
loosely use the name of a side of a triangle for its measure. That is, by saying “a is 5
units” we really mean that “the length of the side a is 5 units”.
The following theorems on triangles that you may have heard about in middle school and
may have proved in high school will be useful throughout this section.
Angle Sum of a Triangle Theorem. The sum of the degrees of the angles of a
triangle is 180◦ .
Pythagorean Theorem. Suppose γ = 90◦ . Then a2 + b2 = c2 .
Converse of the Pythagorean Theorem. Suppose a2 + b2 = c2 . Then γ = 90◦ .
9.1
Solving a Right Triangle
Consider a right triangle. That is, one of the angles is a right angle. Then by the Angle
Sum of a Triangle Theorem, the other two angles are acute.
Let us name the vertices of the given right triangle as follows.
9.1. SOLVING A RIGHT TRIANGLE
173
A
B
C
Then according to our convention, the side AB is c, the side BC is a and the side AC is
b, and the angle B is γ.
A
c
b
B
β
a
C
Introduce a coordinate system and move the triangle ABC by using rigid motions: rotate,
translate, or reflect, so that B is at the origin, and BC is on the positive x axis. Since β
is acute, the point A lies in the first quadrant and the coordinates of A are (a, b).
y
A(a, b)
c
b
β
B
a
C
x
Notice that the angle β is in the standard position and A is a point on the terminal side
of β. Therefore, by the definition of the sine number of β, sin β = cb , and by the definition
of a cosine number of β, cos β = ac . Therefore, a = c cos β and b = c cos β.
174
CHAPTER 9. APPLICATIONS: SOLVING A TRIANGLE
y
A(a, b)
c
b = c sin β
β
B
C
a = c cos β
x
Now if we remove the coordinate system then we have the following information for the
given right triangle.
A
c
c sin β
B
β
C
c cos β
So, for a right triangle, we can think of the measure of the adjacent side of β as c cos β
and the length of the opposite side as c sin β.
Combining the above observations, we have the following theorem. We will deviate from
our convention just for this theorem only to demonstrate that the theorem does not
depend on the convention.
Trigonometric Numbers of a Triangle Theorem. Consider a right triangle and
let θ be one of the acute angles. Then
1. sin θ =
the length of the opposite side
the length of the hypotenuse
9.1. SOLVING A RIGHT TRIANGLE
2. cos θ =
the length of the adjacent side
the length of the hypotenuse
3. tan θ =
the length of the opposite side
the length of the adjacent side
175
Proof. Let ABC be the given triangle and let θ be the angle B as shown. Let AB = c.
Then BC = c cos θ and AC = c sin θ.
A
c
c sin θ
B
θ
C
c cos θ
Therefore,
|AC|
c sin θ
the length of the opposite side
=
=
the length of the hypotenuse
|AB|
c
= sin θ.
the length of the adjacent side
|BC|
c cos θ
=
=
the length of the hypotenuse
|AB|
c
= cos θ.
the length of the opposite side
|AC|
c sin θ
=
=
the length of the adjacent side
|BC|
c cos θ
= tan θ.
Theorem. A right triangle can be solved if a length of a side and the measure of one
acute angle are given.
176
CHAPTER 9. APPLICATIONS: SOLVING A TRIANGLE
Exercise. Prove the above theorem.
Example. Suppose the length of the hypotenuse of a right triangle is 13 units and one of
the acute angles is 31◦ . Solve the triangle.
A
α
13
b
B
Answer. Suppose the given triangle is ABC as shown below.
31◦
C
a
We know that c = 13, β = 31◦ , and γ = 90◦ . We have to find α, a, and b to solve this
triangle.
By the Angle Sum of a Triangle Theorem, α + 31 + 90 = 180, all in degrees. Therefore,
α = 59◦ . b = 13 sin 31◦ . If we want to know this number approximately then we could use
a calculator. With the help of a calculator, b ≈ 6.7 units. a = 13 cos 31◦ . With the help
of a calculator, a ≈ 11.1 units. Therefore,
a ≈ 11.1 length units, b ≈ 6.7 length units, c = 13 units, α = 59◦ , β = 31◦ and
γ = 90◦ .
Theorem. A right triangle can be solved if the lengths of two sides are given.
Exercise. Prove the above theorem.
Example. Suppose the length of the hypotenuse of a right triangle is 13 length units and
one of the other two sides is 11 length units. Solve the triangle.
9.1. SOLVING A RIGHT TRIANGLE
177
A
α
13
b
B
Answer. Suppose the given triangle is ABC as shown below.
β
C
11
We know that c = 13, a = 11, and γ = 90◦ . We have to find α, β, and b to solve this
triangle.
√
By the Pythagorean Theorem, 132 = 112 + b2 . Therefore, b2 = 48 and b = ± 48. Since
√
b is a length, b > 0. Therefore, b = 4 3. By the Trigonometric Numbers of a Triangle
. Notice that this is a trigonometric equation. The general solution
Theorem, cos β = 11
13
−1 11
is 2nπ ± cos
, for any integer n. Since β is acute β is in (0, π2 ). The inverse cosine
13
11
function is defined in this interval, and among all solutions of cos β = 13
, the only solution
π
−1 11
−1 11
in (0, 2 ) is cos
. Therefore, β = cos
. By using a calculator we can find an
13
13
approximation of this number. Accordingly, β ≈ 32◦ . By the Sum of The Angles of a
Triangle Theorem, α ≈ 180◦ − (90◦ + 32◦ ) in degrees. Therefore, α = 58◦ .
√
Now we have all six quantities. a = 11 length units, b = 4 3 length units, c = 13 length
units, α = 58◦ , β = 32◦ , and γ = 90◦ .
178
CHAPTER 9. APPLICATIONS: SOLVING A TRIANGLE
9.2
Solving Triangles that are not Right Triangles
Consider a triangle which is not a right triangle.
A
α
c
B
b
γ
β
a
C
It is important to know that the Pythagorean Theorem is not available any more. However, the Sum of the Angles of a Triangle Theorem is still useful. In addition, the following
theorems that you may have learned in high school can be useful.
Triangle Inequality Theorem. In a triangle, sum of the lengths of two sides is
longer than the length of the third side.
Longer Side of a Triangle Theorem. In a triangle, a side facing a larger angle is
longer.
For example, suppose α > γ. (See the above figure.) Then a > c.
Larger Angle of a Triangle Theorem. In a triangle, an angle facing a longer side
is larger.
For example, suppose c > b. (See the above figure.) Then γ > β.
9.2. SOLVING TRIANGLES THAT ARE NOT RIGHT TRIANGLES
179
ASA Theorem. Consider two triangles A1 B1 C1 and A2 B2 C2 .
1. If α1 = α2 , c1 = c2 , and β1 = β2 , then the two triangles are congruent.
2. If β1 = β2 , a1 = a2 , and γ1 = γ2 , then the two triangles are congruent.
3. If γ1 = γ2 , b1 = b2 , and α1 = α2 , then the two triangles are congruent.
SAS Theorem. Consider two triangles A1 B1 C1 and A2 B2 C2 .
1. If b1 = b2 , α1 = α2 , and c1 = c2 , then the two triangles are congruent.
2. If c1 = c2 , β1 = β2 , and a1 = a2 , then the two triangles are congruent.
3. If a1 = a2 , γ1 = γ2 , and b1 = b2 , then the two triangles are congruent.
SSS Theorem. Consider two triangles A1 B1 C1 and A2 B2 C2 .
If a1 = a2 , b1 = b2 , and c1 = c2 , then the two triangles are congruent.
Cross Multiplication Algorithm Theorem. If A, B, C and D are real numbers
and B 6= 0 and D 6= 0, then
AD = BC if and only if
C
A
= .
B
D
180
CHAPTER 9. APPLICATIONS: SOLVING A TRIANGLE
9.3
Law of Sines
The Law of Sines Theorem. Let ABC be a triangle with the standard notations.
Then
sin α
sin β
sin γ
=
=
.
a
b
c
sin α
sin β sin β
sin γ
sin α
sin γ
That is, we have to show that
=
,
=
, and
=
to prove
a
b
b
c
a
c
this theorem. Since the equality is transitive for real numbers, if we can prove the first
two then the third follows. Any angle (measure) of a triangle lies in the interval (0, π).
Therefore, sin α 6= 0, sin β 6= 0, and sin γ 6= 0. Clearly, a 6= 0, b 6= 0, and c 6= 0. Then by
using the Cross Multiplication Algorithm Theorem, we also get:
a
b
c
=
=
.
sin α
sin β
sin γ
We will prove
sin β
sin γ
=
and leave the proof of the other half as an exercise.
b
c
Proof. Drop a perpendicular from A to the side BC. Let D be the foot of this perpendicular. There are two cases. The point D lies between B and C or D lies outside of
BC.
A
c
B
b
γ
β
C
D
In the first case, from the right triangle ABD, we get |AD| = c sin β, and from the triangle
ACD, we get |AD| = b sin γ. Therefore,
c sin β = b sin γ.
9.3. LAW OF SINES
181
By using the Cross Multiplication Algorithm,
sin β
sin γ
=
.
b
c
A
c
B
β
b
γ
C
D
In the second case, let us assume that D lies on the extended segment BC as shown in
the figure. Then from the right triangle ABD we get |AD| = c sin β and from the triangle
ACD we get |AD| = b sin(180◦ − γ). Since the sine function is symmetrical with respect
to the line x = π2 , sin(180◦ − γ) = sin γ. Therefore,
c sin β = b sin γ.
By using the Cross Multiplication Algorithm Theorem,
sin β
sin γ
=
.
b
c
Exercise. Let ABC be a triangle with standard notations. Show that
sin β
sin α
=
.
a
b
Example. Let ABC be the triangle with standard notations. Suppose β = 20◦ , a = 7
units, γ = 40◦ . Solve the triangle, if possible.
Answer. First notice that we can easily construct a triangle with the given properties by
using a ruler and a compass. That is, a triangle with the given properties exists. By the
ASA Theorem, there is only one such triangle up to a congruence. That is, any other
triangle with these properties is congruent to this triangle. We have to find α, b and c to
solve the triangle.
182
CHAPTER 9. APPLICATIONS: SOLVING A TRIANGLE
A
α
c
B
b
20◦
40◦
C
7
By the Sum of the Angles of a Triangle Theorem, α = 120◦ . By the Law of Sines Theorem,
b
7
=
.
◦
sin 20
sin 120◦
By using the Cross Multiplication Algorithm Theorem,
b=
7 sin 20◦
sin 120◦
By using a calculator, b ≈ 2.7 units. By the Law of sines Theorem,
c
7
=
.
◦
sin 40
sin 120◦
By using the Cross Multiplication Algorithm Theorem,
c=
7 sin 40◦
sin 120◦
By using a calculator, c ≈ 5.2 units.
Now we have all six quantities. a = 7 length units, b ≈ 2.7 length units, c ≈ 5.2 length
units, α = 120◦ , β = 20◦ and γ = 40◦ .
Example. Let ABC be the triangle with standard notations. Suppose β = 120◦ , a = 7
units, γ = 70◦ . Solve the triangle, if possible.
Answer. Since 120◦ + 70◦ > 180◦ , there is no such triangle, by the Angle Sum of a
Triangle Theorem.
Example. Let ABC be the triangle with standard notations. Suppose β = 20◦ , a = 7
units, b = 3 units. Solve the triangle, if possible.
Answer. With the result of the previous example, we know that it is possible that there
may be no triangle with the given properties. Instead of trying to construct a triangle with
the given properties, let us assume that the given triangle exists and use known theorems,
9.3. LAW OF SINES
183
and try to solve the triangle. In the process, if we encounter a contradiction, then we
know that our assumption is false and there can be no such triangle.
So, let us assume that there is such a triangle.
A
α
c
B
3
γ
20◦
C
7
First we can find α by using the Law of Sines Theorem.
sin α
sin 20◦
=
.
7
3
By the Cross Multiplication Algorithm Theorem,
sin α =
7 sin 20◦
.
3
An angle of a triangle is greater than 0◦ and less than 180◦ . That is, we have a sine
equation in α, and we want to find the solutions in the interval (0◦ , 180◦ ). The general
solution (in degrees) is:
7 sin 20◦
◦
n
−1
α = n(180 ) + (−1) sin
, where n is any integer.
3
when n = 0, we get,
7 sin 20◦
−1
α = sin
3
and when n = 1, we get,
7 sin 20◦
◦
−1
α = 180 − sin
3
It would be hard to proceed without knowing approximately what sin−1 7 sin320
will use a calculator to get an approximation of this quantity. It turns out,
7 sin 20◦
−1
sin
≈ 53◦ .
3
◦
is. We
184
CHAPTER 9. APPLICATIONS: SOLVING A TRIANGLE
Therefore, α ≈ 53◦ or α ≈ 127◦ .
case 1: α ≈ 53◦ .
By the Sum of the Angles of a Triangle Theorem, γ = 107◦ . By the Law of Sines Theorem,
c
3
=
.
sin γ
sin 20◦
By the Cross Multiplication Algorithm theorem,
c=
3 sin γ
.
sin 20◦
By using a calculator, c ≈ 8.4 units.
case 2: α ≈ 127◦ .
By the Sum of the Angles of a Triangle Theorem, γ = 33◦ . By the Law of Sines Theorem,
3
c
=
.
sin γ
sin 20◦
By the Cross Multiplication Algorithm theorem,
c=
3 sin γ
.
sin 20◦
By using a calculator, c ≈ 4.8 units.
There are two triangles with the given properties.
1. a = 7, b = 3, c ≈ 8.4,α ≈ 53◦ , β = 20◦ , γ ≈ 107◦ .
2. a = 7, b = 3, c ≈ 4.8,α ≈ 127◦ , β = 20◦ , γ ≈ 33◦
Example. Let ABC be the triangle with standard notations. Suppose β = 80◦ , a = 7
units, b = 3 units. Solve the triangle, if possible.
Answer. Suppose there is a triangle with the given properties.
A
α
c
3
γ
◦
B 80
7
C
9.3. LAW OF SINES
185
By the Law of Sines Theorem,
sin α
sin 80◦
=
.
7
3
By the Cross Multiplication Algorithm,
sin α =
7 sin 80◦
.
3
That is,
sin α ≈ 2.29788
This is impossible since −1 ≤ sin α ≤ 1. Therefore, our assumption is false. That is,
there is no such triangle.
Example. Let ABC be the triangle with standard notations. Suppose β = 87◦ , a = 6.8
units, b = 7 units. Solve the triangle, if possible.
Answer. Suppose there is a triangle with the given properties.
A
α
c
7
γ
◦
B 87
C
6.8
By the Law of Sines Theorem,
sin α
sin 87◦
=
.
6.8
7
By the Cross Multiplication Algorithm,
6.8 sin 87◦
sin α =
.
7
The general solution to this equation is:
6.8 sin 87◦
◦
n
−1
α = n(180 ) + (−1) sin
, where n is any integer.
7
186
CHAPTER 9. APPLICATIONS: SOLVING A TRIANGLE
when n = 0, we get,
6.8 sin 87◦
−1
α = sin
≈ 76◦
7
and when n = 1, we get,
6.8 sin 87◦
◦
−1
≈ 104◦
α = 180 − sin
7
case 1: α ≈ 76◦ .
By the Sum of the Angles of a Triangle Theorem, γ = 17◦ . By the Law of Sines Theorem,
c
3
=
.
sin γ
sin 20◦
By the Cross Multiplication Algorithm theorem,
c=
3 sin γ
.
sin 20◦
By using a calculator, c ≈ 2.05 units.
case 2: α ≈ 104◦ .
Since 87◦ + 104◦ > 180◦ , there is no such triangle by the Sum of the Angles of a Triangle
Theorem.
There is one triangle with the given properties.
a = 6.8, b = 7, c ≈ 2.05,α ≈ 76◦ , β = 87◦ , γ ≈ 17◦ .
Example. Let ABC be the triangle with standard notations. Suppose β = 40◦ , a = 6.8
units, c = 7 units. Solve the triangle, if possible.
We cannot solve this triangle by using only the known theorems.
Example. Let ABC be the triangle with standard notations. Suppose a = 6.8, b = 5.7
units, c = 4.9 units. Solve the triangle, if possible.
We cannot solve this triangle by using only the known theorems. We need a new tool to
solve the triangles in the last two examples.
9.4. LAW OF COSINES
9.4
187
Law of Cosines
We encountered two situations where we could not solve a given triangle by using the
known theorems. We will develop a new tool for this purpose.
Law of Cosines Theorem. Consider a triangle ABC with standard notations. Then
1. a2 = b2 + c2 − 2bc cos α
2. b2 = c2 + a2 − 2ca cos β
3. c2 = a2 + b2 − 2ab cos γ
Proof. We will prove a2 = b2 + c2 − 2bc cos α. The proofs of the other two parts are similar
and therefore, left as exercises.
Drop a perpendicular from A to BC. Let the foot of this perpendicular be D. As we
have observed before, D can lie within the segment BC or outside of the segment BC.
Consider the case where D lies within BC.
A
c
B
b
γ
β
C
D
By using the Pythagorean Theorem on the right triangle ACD we get:
|AC|2 = |AD|2 + |DC|2
In this case, |DC| = |BC| − |BD|. That is, |DC| = a − c cos β. Also, |AD| = c sin β.
Therefore,
b2 = (a − c cos β)2 + c2 sin2 β.
That is,
b2 = a2 − 2ac cos β + c2 cos2 β + c2 sin2 β.
(1)
188
CHAPTER 9. APPLICATIONS: SOLVING A TRIANGLE
By using the Pythagorean Theorem on the right triangle ABD we get:
|AB|2 = |AD|2 + |BD|2
That is,
c2 = c2 sin2 β + c2 cos2 β.
(2)
By substituting c2 for c2 sin2 β + c2 cos2 β in (1):
b2 = a2 − 2ac cos β + c2 .
or
b2 = c2 + a2 − 2ca cos β.
Now consider the second case, where D lies outside of BC.
A
c
B
b
γ
β
a
C
D
By using the Pythagorean Theorem on the right triangle ACD we get:
|AC|2 = |AD|2 + |CD|2
In this case, |CD| = |BD| − |BC|. That is, |CD| = c cos β − a. Also, |AD| = c sin β.
Therefore,
b2 = (c cos β − a)2 + c2 sin2 β.
That is,
b2 = c2 cos2 β − 2ac cos β + a2 + c2 sin2 β.
(3)
By using the Pythagorean Theorem on the right triangle ABD we get:
|AB|2 = |AD|2 + |BD|2
9.4. LAW OF COSINES
189
That is,
c2 = c2 sin2 β + c2 cos2 β.
(4)
By substituting c2 for c2 sin2 β + c2 cos2 β in (3):
b2 = c2 − 2ac cos β + a2 .
or
b2 = c2 + a2 − 2ca cos β.
Exercise. Consider a triangle ABC with standard notations. Show that
1. a2 = b2 + c2 − 2bc cos α
2. c2 = a2 + b2 − 2ab cos γ
The Law of Cosines Theorem is a generalization of the Pythagorean Theorem in the
following sense. Consider the statement c2 = a2 + b2 − 2ab cos γ. Since γ is an angle of a
triangle, the degree measure of γ can be any value between 0◦ and 180◦ , exclusively. In
the special case if γ = 90◦ , then cos γ = 0 and we get, c2 = a2 + b2 .
Example. Let ABC be the triangle with standard notations. Suppose β = 40◦ , a = 6.8
units, c = 7 units. Solve the triangle, if possible.
Answer. By the SAS theorem, there is only one such triangle up to a congruence.
A
α
7
B
b
γ
40◦
C
6.8
By the Law of Cosines Theorem,
b2 = 72 + 6.82 − 2(7)(6.8) cos 40◦
190
CHAPTER 9. APPLICATIONS: SOLVING A TRIANGLE
Since b > 0,
p
b = 72 + 6.82 − 2(7)(6.8) cos 40◦ ≈ 4.7.
By the Law of Cosines Theorem,
6.82 = 72 + b2 − 2(7)(b) cos α
That is,
cos α ≈
72 + 4.72 − 6.82
2(7)(4.7)
We want to find the solution to this equation between 0◦ and 180◦ . By the definition of
the inverse cosine function, the only solution of this equation between 0◦ and 180◦ is
2
7 + 4.72 − 6.82
−1
≈ 67.8◦ .
α = cos
2(7)(4.7)
Now, by the Sum of the Angles of a Triangle Theorem,
γ = 180◦ − α − β ≈ 72.2◦ .
Therefore,
a = 6.8 units, b ≈ 4.7 units, c = 7 units, α ≈ 67.8◦ , β = 40◦ , and γ ≈ 72.2◦ .
Example. Let ABC be the triangle with standard notations. Suppose a = 6.8, b = 5.7
units, c = 4.9 units. Solve the triangle, if possible.
Answer. By the SSS theorem, there is only one such triangle up to a congruence.
A
α
4.9
B
5.7
γ
β
C
6.8
By the Law of Cosines Theorem,
6.82 = 4.92 + 5.72 − 2(4.9)(5.7) cos α
That is,
cos α ≈
4.92 + 5.72 − 6.82
2(4.9)(5.7)
9.4. LAW OF COSINES
191
By the definition of the inverse cosine function, the only solution of this equation between
0◦ and 180◦ is
2
4.9 + 5.72 − 6.82
−1
α = cos
≈ 79.4◦ .
2(4.9)(5.7)
By the Law of Cosines Theorem,
5.72 = 4.92 + 6.82 − 2(4.9)(6.8) cos β
That is,
cos β ≈
4.92 + 6.82 − 5.72
2(4.9)(6.8)
By the definition of the inverse cosine function, the only solution of this equation between
0◦ and 180◦ is
2
4.9 + 6.82 − 5.72
−1
≈ 55.5◦ .
β = cos
2(4.9)(6.8)
Now, by the Sum of the Angles of a Triangle Theorem,
γ = 180◦ − α − β ≈ 45.1◦ .
Therefore,
a = 6.8 units, b = 5.7 units, c = 4.9 units, α ≈ 79.4◦ , β ≈ 55.5◦ , and γ ≈ 45.1◦ .
Chapter 10
Applications: Area of a Triangle
Consider a given triangle with standard notations. Our next goal is to find the area of
such a triangle. You may have learned in high school a theorem stating that the area of a
triangle is “ 21 (base)(height)”. We will use this theorem and the knowledge of Trigonometry
to find a few results that can be used to calculate the area of a triangle.
Area of a Triangle Theorem. Let ABC be a triangle with standard notations. Then
1. the area of the triangle = 12 bc sin α
2. the area of the triangle = 12 ca sin β
3. the area of the triangle = 12 ab sin γ
Proof. We will prove the second statement and leave the proof the other two as exercises.
Drop a perpendicular from A to BC. Let the foot of this perpendicular be D. There are
two cases; D lies within the segment BC or D lies outside of the segment BC. Consider
the case where D lies within the segment BC (In case ABC is a right angle with γ = 90◦ ,
then D = C).
A
c
B
β
C
D
193
194
CHAPTER 10. APPLICATIONS: AREA OF A TRIANGLE
Then |AD| = c sin β. Therefore, the area of the triangle = 12 (base)(height) = 12 (|BC|)(|AD|) =
1
(a)(c sin β) = 12 ca sin β.
2
Now consider the case where D lies outside of the segment BC.
A
c
B
β
a
C
D
Then |AD| = c sin β. Therefore, the area of the triangle = 12 (base)(height) = 12 (|BC|)(|AD|) =
1
(a)(c sin β) = 12 ca sin β.
2
Exercise. Prove the other two parts of the theorem.
Example. Let ABC be a triangle with standard notations and let c = 7 units, β = 20◦ ,
and a = 8 units. Find the area of the triangle.
Answer. By the SAS Theorem, there is only one such triangle up to a congruence.
A
7
B
20◦
C
8
By the Area of a Triangle Theorem, the area of the triangle is 12 (8)(7 sin 20◦ ) ≈ 9.58 area
units.
Example. Let ABC be a triangle with standard notations and let β = 20◦ ,a = 8 units,
and γ = 40◦ . Find the area of the triangle.
Answer. By the ASA Theorem, there is only one such triangle up to a congruence. By
the Sum of the Angles of a Triangle Theorem, α = 120◦ .
A
α
c
B
20◦
40◦ C
8
195
By the Law of Sines Theorem,
c
8
=
◦
sin 40
sin 120◦
By the Cross Multiplication Algorithm Theorem,
8 sin 40◦
c=
sin 120◦
Now by the Area of a Triangle Theorem, the area of the triangle is
8 sin 40◦
1
(8)
sin 20◦ ≈ 8.12 area units.
◦
2
sin 120
Example. Let ABC be a triangle with standard notations and let ,a = 8 units, b = 4
units, and c = 7 units. Find the area of the triangle.
Answer. By the SSS Theorem, there is only one such triangle up to a congruence.
A
7
4
β
B
C
8
By the Law of Cosines Theorem,
42 = 72 + 82 − 2(7)(8) cos β
That is
72 + 82 − 42
2(7)(8)
cos β =
and
−1
β = cos
72 + 82 − 42
2(7)(8)
.
Now by the Area of a Triangle Theorem, the area of the triangle is
2
1
7 + 82 − 42
−1
≈ 14 area units.
(7)(8) sin cos
2
2(7)(8)
196
CHAPTER 10. APPLICATIONS: AREA OF A TRIANGLE
10.1
Heron’s Formula
There is an ingenious theorem discovered by the Greek mathematicians about 2000 years
ago to calculate the area of a triangle when you know the lengths of its three sides.
Ancient Greeks visualized numbers as lengths of segments. That is, a product of two
numbers represented an area, and the product of three numbers represented a volume.
This theorem contains a product of four numbers, and it did not represent anything that
they knew of. Yet they discovered that the square-root of a product of a certain four
numbers associated with a given triangle is the area of the triangle. This theorem is
known today as Heron’s Formula in honor of Heron of Alexandria (10 - 70 AD.)
Heron’s Formula Theorem. Let ABC be a triangle with standard notations. Let
s be the semi-perimeter of the triangle. That is, s = (a + b + c)/2. Then the area of the
p
triangle is s(s − a)(s − b)(s − c).
Let us re-do the previous example now using the Heron’s Formula Theorem before proving
the Heron’s Formula Theorem.
Example. Let ABC be a triangle with standard notations and let a = 8 units, b = 4
units, and c = 7 units. Find the area of the triangle.
Answer. The semi-perimeter s of this triangle is 8+4+7
=
2
Theorem, the area of the triangle is
s 19 19
19
19
−8
−4
− 7 ≈ 14 area units.
2
2
2
2
19
.
2
By the Heron’s Formula
The following is the proof of the Heron’s Formula Theorem based on what we have learned
up to now.
Proof. Let us examine what those four numbers are in the formula first. We know what
s is.
a+b+c
a + b + c 2a
b+c−a
−a=
−
=
.
2
2
2
2
a+b+c
a + b + c 2b
a+c−b
s−b=
−b=
−
=
.
2
2
2
2
s−a=
(10.1)
10.1. HERON’S FORMULA
s−c=
197
a+b+c
a + b + c 2c
a+b−c
−c=
−
=
.
2
2
2
2
Let A be the area of the triangle. Then by the Area of a Triangle Theorem,
1
A = ca sin β.
2
That is,
1
A2 = c2 a2 sin2 β.
4
By using the Pythagorean Theorem on the triangle ABD in either of the following figures,
we get:
c2 = c2 cos2 β + c2 sin2 β.
A
A
c
B
c
β
C
D
The above equation can be written as:
c2 sin2 β = c2 − c2 cos2 β.
By multiplying both sides by a2 , we get:
c2 a2 sin2 β = c2 a2 − c2 a2 cos2 β.
Now substitute the above in A2 :
A2 =
1 2 2
c a − c2 a2 cos2 β .
4
By the Law of Cosines Theorem,
b2 = c2 + a2 − 2ca cos β.
The above equation can be written as:
1
ca cos β = (c2 + a2 − b2 ).
2
B
β
a
C
D
198
CHAPTER 10. APPLICATIONS: AREA OF A TRIANGLE
Substitute the above in A2 :
1 2 2 1 2
2
2
2 2
A =
c a − (c + a − b )
4
4
The above equation can be written as:
A2 =
1
4c2 a2 − (c2 + a2 − b2 )2
16
(10.2)
By using the Difference of Squares Identity in (2):
A2 =
1
2ca − (c2 + a2 − b2 ) 2ca + (c2 + a2 − b2 )
16
The above equation is the same as:
A2 =
1 2
b − (c2 − 2ca + a2 ) (c2 + 2ac + a2 ) − b2 )
16
By the Binomial Square Identities:
A2 =
1 2
b − (c − a)2 (c + a)2 − b2 )
16
(10.3)
By using the Difference of Squares Identity in (3):
A2 =
1
(b − (c − a))(b + (c − a))(c + a) − b)(c + a) + b)
16
That is,
A2 =
1
(a + b − c)(b + c − a)(c + a − b)(a + b + c)
16
The above equation is the same as:
A2 =
(a + b − c) (b + c − a) (c + a − b) (a + b + c)
2
2
2
2
By using (1):
A2 = (s − c)(s − a)(s − b)s
Since A > 0,
p
A = s(s − a)(s − b)(s − c)
Now to tie up some loose ends, notice that a + b > c, b + c > a and c + a > b by the
Triangle Inequality Theorem. Therefore, s − a, s − b and s − c are all positive quantities.
Chapter 11
Applications: Trigonometric
Identities
Recall that an algebraic equation that is true for all real numbers is called an identity.
For example, x2 − a2 = (x − a)(x + a) is true for any real number x and for any real
number a. We relaxed the strict requirement that an identity must be true for all real
numbers to include the following as an algebraic identity.
a c
ad + bc
+ =
, for all real numbers a, b, c, and d except b = 0 and c = 0.
b d
bd
The above identity is true for all real numbers except for few real numbers.
We will relax the requirement even further to include an important list of trigonometric equations as trigonometric identities. For example, we want to call the following a
trigonometric identity.
tan x =
sin x
, where x is a real number.
cos x
As you know that there are countably many real numbers where cos x = 0. The general
solution of the equation cos x = 0 is 2nπ ± π2 , for any integer n. In other words, the above
equation is not true for countably many numbers. However, the equation is true for many
more numbers.1
1
The equation is true for uncountably many numbers. In mathematical parlance, the identity is true
for all numbers except for a set whose measure is 0. The explanation of what that means is beyond our
comprehension at the moment.
199
200
CHAPTER 11. APPLICATIONS: TRIGONOMETRIC IDENTITIES
11.1
Basic Trigonometric identities
We will start with definitions of tangent, secant, cosecant, and cotangent numbers of
a given real number. They are trigonometric identities by the above description of a
trigonometric identity.
Let θ be any real number. Then
tan θ =
sin θ
cos θ
csc θ =
1
sin θ
sec θ =
1
cos θ
cot θ =
cos θ
sin θ
(A)
Let us revisit the unit circle to identify several more basic trigonometric identities.2 For
co-terminal angles in standard position, the following are always true.
Suppose θ is a given angle in radians. Then there is an angle α in the standard position
so that 0 ≤ α < 2π and θ and α are co-terminal. That is, there is an integer k so that
θ = 2kπ + α.
P (a, b)
α
2
You can obtain the same identities by examining the graphs of trigonometric functions.
11.1. BASIC TRIGONOMETRIC IDENTITIES
201
Since θ and α are co-terminal angles, the point of intersection of the terminal side and
the unit circle, say P (a, b), is the same for both angles. In addition, any angle of the form
2nπ + θ is co-terminal with θ, for any integer n. Therefore, we have the following two
identities.
For any angle θ and for any integer n,
sin(2nπ + θ) = sin θ
(B)
cos(2nπ + θ) = cos θ
Since any given angle θ in standard position is co-terminal to an angle α in standard
position, where 0 ≤ α < 2π, and sin θ = sin α and cos θ = cos α, we will just look at an
arbitrary angle in [0, 2π) to obtain the following identities.
Consider any angle θ in the standard position. Let P (a, b) be the point of intersection
between the terminal side of θ and the unit circle. We can obtain the angle −θ in the
standard position by reflecting the angle θ about the x-axis. Then the point of intersection
Q between the terminal side of −θ and the unit circle has coordinates (a, −b).
P (a, b)
θ
−θ
Q(a, −b)
As a result we have two new identities.
202
CHAPTER 11. APPLICATIONS: TRIGONOMETRIC IDENTITIES
For any angle θ,
cos(−θ) = cos θ
(C)
sin(−θ) = − sin θ
Consider any angle θ in the standard position. Let P (a, b) be the point of intersection of
θ and the unit circle. Then a = cos θ and b = sin θ, by definition.
P (cos θ, sin θ)
θ
O
By the Distance Formula Theorem,
p
|P O| = (cos θ − 0)2 + (sin θ − 0)2
But |P O| is the radius of the unit circle. That is, |P O| = 1. Therefore,
p
1 = (cos θ)2 + (sin θ)2
By squaring both sides of the above equation we get the following important trigonometric
identity.
For any angle θ,
cos2 θ + sin2 θ = 1.
(D)
11.1. BASIC TRIGONOMETRIC IDENTITIES
203
By subtracting sin2 θ from both sides of (D), you get the following trigonometric identity.
For any angle θ,
cos2 θ = 1 − sin2 θ.
By subtracting cos2 θ from both sides of (D), you get the following trigonometric identity.
For any angle θ,
sin2 θ = 1 − cos2 θ.
By dividing both sides of (D) by cos2 θ and using the identities in (A), you get the
following trigonometric identity.
For any angle θ,
1 + tan2 θ = sec2 θ.
By subtracting 1 from both sides of the above identity, you get the following identity.
For any angle θ,
tan2 θ = sec2 θ − 1.
By dividing both sides of (D) by sin2 θ and using the identities in (A), you get the following
trigonometric identity.
For any angle θ,
cot2 θ + 1 = csc2 θ.
By subtracting 1 from both sides of the above identity, you get the following identity.
For any angle θ,
cot2 θ = csc2 θ − 1.
Since all the previous six identities are direct descendants of the identity (D) we will list
them together.
204
CHAPTER 11. APPLICATIONS: TRIGONOMETRIC IDENTITIES
For any angle θ,
cos2 θ + sin2 θ = 1
(E)
cos2 θ = 1 − sin2 θ
sin2 θ = 1 − cos2 θ
1 + tan2 θ = sec2 θ
tan2 θ = sec2 θ − 1
cot2 θ + 1 = csc2 θ
cot2 θ = csc2 θ − 1
We need one more basic trigonometric identity before we proceed. For this we need to
use another theorem that you may have learned in high school.
Slopes of Perpendicular Lines Theorem. Suppose two lines `1 and `2 are perpendicular to each other. Suppose the slope of the line `1 is m1 and the slope of the line
`2 is m2 . Then m1 · m2 = −1.
Let us first observe a few properties of the coordinate system. Let us pick a point P1 (a1 , b1 )
in the first quadrant. Then the signs of the coordinates of P1 are both positive. We will
indicate this by (+, +). Rotate the plane about O by an angle of π2 counterclockwise.
Suppose the rotated P1 is P2 (a2 , b2 ). Then P2 is in the second quadrant and the signs of
coordinates of P2 are (−, +). Rotate the plane about O by an angle of π2 counterclockwise
again. Suppose the rotated P2 is P3 (a3 , b3 ). Then P3 is in the third quadrant and the
signs of coordinates of P3 are (−, −). Rotate the plane about O by an angle of π2 counterclockwise again. Suppose the rotated P3 is P4 (a4 , b4 ). Then P4 is in the fourth quadrant
and the signs of coordinates of P4 are (+, −).
11.1. BASIC TRIGONOMETRIC IDENTITIES
205
P1 (a1 , b1 )
(+, +)
P2 (a2 , b2 )
(−, +)
O
P2 (a2 , b2 )
(+, −)
P3 (a3 , b3 )
(−, −)
If we rotate the plane one more time about O by an angle of
the image of P4 under this rotation will be P1 .
π
2
counterclockwise, then
Notice that after each rotation, the sign of the y-coordinate of the new point is the sign
of the x-coordinate of the previous point. For example, the sign of the y-coordinate of P3
is the sign of the x-coordinate of P2 . Also notice that the sign of the x-coordinate of the
new point is the opposite sign of the y-coordinate of the previous point.
Next we will look at the relationships of the coordinates of a point and the rotated image
of the point. Without loss of generality, let us look at P1 and P2 . Let us assume that P1
lies on the unit circle. Then P2 lies on the unit circle as well, as rotations preserve lengths
of line segments. The slope of the line LOP1 is ab11−0
= ab11 . The slope of the line LOP2 is
−0
b2 −0
= ab22 . Since LOP1 is perpendicular to LOP2 , by the Slopes of the Perpendicular Lines
a2 −0
Theorem,
b1
b2
·
= −1.
a1
a2
Therefore, by the Cross-Multiplication Algorithm Theorem,
b1
a2 = −
b2 .
a1
Since, P2 is a point on the unit circle,
a22 + b22 = 1.
2
b1
=⇒ −
b2 + b2 = 1.
a1
206
CHAPTER 11. APPLICATIONS: TRIGONOMETRIC IDENTITIES
=⇒ b22
=⇒
b22
b1
a1
!
2
+1
b21 + a21
a21
= 1.
= 1.
Since (a1 , b1 ) is on the unit circle, a21 + b21 = 1. Therefore,
b22
1
a21
= 1.
By the Cross Multiplication Algorithm Theorem,
b22 = a21 .
By the Square-Root Principle Theorem,
b2 = ±a1 .
By substituting the values of b2 into a2 ,
a2 = ∓b1 .
In other words, (a2 , b2 ) is either (b1 , −a1 ) or (−b1 , a1 ). Since the rotation is counterclockwise, (a2 , b2 ) is (−b1 , a1 ). As a result, we have the following identities.
For any angle θ,
π
cos θ +
= − sin θ
2
π
sin θ +
= cos θ
2
(H)
We claim that the identities in (H) are true for any angle θ. However we did not show
that the above identities are true if the terminal side of the angle θ is on one of the axes.
I will leave it as an exercise for you to prove that fact.
Exercise. Show that the identities in (H) are true if the terminal side of θ lies on one of
the axes.
11.2. SUM AND DIFFERENCE IDENTITIES
11.2
207
Sum and Difference Identities
The next four trigonometric identities that we are going to prove are extremely important. I would like to refer to these four trigonometric identities as the super-stars of
trigonometric identities.
Consider two angles α and β. Without loss of generality, let us assume that α ≥ β. Since
any angle is a co-terminal angle of an angle in the interval [0, 2π), we will also assume that
both α and β are in the interval [0, 2π). Let P be the point of intersection of the terminal
side of α and the unit circle, and let Q be the point of intersection of the terminal side of
β and the unit circle. Then P has the coordinates (cos α, sin α) and Q has the coordinates
(cos β, sin β).
P (cos α, sin α)
Q(cos β, sin β)
α−β
O
By the Distance Formula Theorem, the length of the segment P Q is:
|P Q| =
p
(cos α − cos β)2 + (sin α − sin β)2 .
Now rotate the plane about O by an angle β clockwise. Suppose the image of P under
this rotation is P 0 and the image of Q under this rotation is Q0 .
208
CHAPTER 11. APPLICATIONS: TRIGONOMETRIC IDENTITIES
P 0 (cos(α − β), sin(α − β))
α−β
O
Q0 (1, 0)
Since rotations preserve the measures of angles, the angle ∠Q0 OP 0 = α − β. Since the
angle ∠Q0 OP 0 is in the standard position, the coordinates of P 0 are (cos(α−β), sin(α−β))
and the coordinates of Q0 are (1, 0). Therefore, the length of the segment P 0 Q0 is:
p
|P 0 Q0 | = (cos(α − β) − 1)2 + (sin(α − β) − 0)2 .
Since rotations preserve lengths of segments, |P Q| = |P 0 Q0 |. Therefore,
p
p
(cos α − cos β)2 + (sin α − sin β)2 = (cos(α − β) − 1)2 + (sin(α − β))2 .
By squaring both sides, we get:
(cos α − cos β)2 + (sin α − sin β)2 = (cos(α − β) − 1)2 + (sin(α − β))2 .
By using the Binomial Identity:
(cos2 α − 2 cos α cos β + cos2 β) + (sin2 α − 2 sin α sin β + sin2 β)
= (cos2 (α − β) − 2 cos(α − β) + 1) + sin2 (α − β).
By using the identity (D), we get:
(1 − 2 cos α cos β) + (1 − 2 sin α sin β) = (2 − 2 cos(α − β).
11.2. SUM AND DIFFERENCE IDENTITIES
209
Subtract 2 from both sides:
2 cos α cos β − 2 sin α sin β = −2 cos(α − β).
By dividing both sides by −2 we get:
For any angle α and for any angle β,
cos(α − β) = cos α cos β + sin α sin β.
(I)
For any angle α and for any angle β, α + β = α − (−β). Therefore, by using the identity
(I) we get:
cos(α + β) = cos(α − (−β))
= cos α cos(−β) + sin α sin(−β).
By the identity (C), cos(−β) = cos β and sin(−β) = − sin β. Therefore:
For any angle α and for any angle β,
cos(α + β) = cos α cos β − sin α sin β.
(J)
By the identity (H), sin(α + β) = − cos π2 + (α + β) . Therefore,
π
+ (α + β)
sin(α + β) = − cos
2 π
= − cos
+α +β
2
π
π
= − cos
+ α cos β − sin
+ α sin β
π2 π2 + α cos β + sin
+ α sin β
= − cos
2
2
by the identity (J). Now by using the identity (H) again, we get the following identity.
For any angle α and for any angle β,
sin(α + β) = sin α cos β + cos α sin β
(K)
210
CHAPTER 11. APPLICATIONS: TRIGONOMETRIC IDENTITIES
For any angle α and for any angle β, α − β = α + (−β). Therefore, by using identity (K),
we get:
sin(α − β) = sin(α + (−β))
= sin α cos(−β) + cos α sin(−β).
By identity (C), cos(−β) = cos β and sin(−β) = − sin β. Therefore:
For any angle α and for any angle β,
sin(α − β) = sin α cos β − cos α sin β.
(L)
The identities (I) – (L) are known as the Sum-Difference Identities. These are the superstars of all trigonometric identities. Now let us demonstrate some of the powers of the
identities (I) – (L).
Example. If we choose α = β in identity (I) we get
cos(α − α) = cos α cos α + sin α sin α
That is,
cos 0 = cos2 α + sin2 α
Since cos 0 = 1, we get identity (D).
1 = cos2 α + sin2 α.
Example. If we choose α = 0 in identity (I) we get
cos(0 − β) = cos 0 cos β + sin 0 sin β
Since cos 0 = 1 and sin 0 = 0, we get one of the identities in (B).
cos(−β) = cos β.
Example. If we choose α = 0 in identity (L), we get
sin(0 − β) = sin 0 cos β − cos 0 sin β
Since cos 0 = 1 and sin 0 = 0, we get the identity in (B).
sin(−β) = − sin β.
11.2. SUM AND DIFFERENCE IDENTITIES
211
Since we know the trigonometric numbers of special angles, by using those values with
our super-star identities, we can find exact trigonometric numbers of a few more angles.
Example.
sin(15◦ ) = sin(45◦ − 30◦ )
= sin 45◦ cos 30◦ − cos 45◦ sin 30◦
√
√
1
3
1
1
=√ ·
−√ ·
2 2
2 2
√
3−1
= √ .
2 2
Exercise.
1.
2.
3.
4.
5.
Find
Find
Find
Find
Find
the
the
the
the
the
exact
exact
exact
exact
exact
value
value
value
value
value
of
of
of
of
of
cos(15◦ ).
cos(75◦ ).
sin(75◦ ).
cos(105◦ ).
sin(105◦ ).
Exercise. Show that for any angle α and for any angle β, where tan α and tan β is
defined,
tan(α + β) =
tan α + tan β
.
1 − tan α tan β
(M)
Exercise. Show that for any angle α and for any angle β, where tan α and tan β is
defined,
tan(α − β) =
tan α − tan β
.
1 + tan α tan β
(N)
In the next two sections, we will see many more applications of the super-star identities.
212
CHAPTER 11. APPLICATIONS: TRIGONOMETRIC IDENTITIES
11.3
Double-angle identities
The following are the super-star identities.
For any angle α and for any angle β,
cos(α − β) = cos α cos β + sin α sin β
(I)
cos(α + β) = cos α cos β − sin α sin β
(J)
sin(α + β) = sin α cos β + cos α sin β
(K)
sin(α − β) = sin α cos β − cos α sin β
(L)
If we choose β = α in (J), then we get:
cos(α + α) = cos α cos α − sin α sin α
That is,
For any angle α
cos 2α = cos2 α − sin2 α
(O)
The identity in (O) is known as one of the double-angle identities. The identities (D) and
(O) together form a nice pair of identities.3
For any angle α
3
1 = cos2 α + sin2 α
(D)
cos 2α = cos2 α − sin2 α
(M)
There is a class of functions called the Hyperbolic Functions. You will learn about them in an
advanced algebra course or in a calculus course. There is a pair of hyperbolic identities similar to these
two trigonometric identities. Namely 1 = cosh2 α − sinh2 α and cosh 2α = cosh2 α + sinh2 α.
11.3. DOUBLE-ANGLE IDENTITIES
213
By using the identity cos2 α = 1 − sin2 α in identity (O), we get:
cos 2α = 1 − 2 sin2 α
By using the identity sin2 α = 1 − cos2 α in identity (O), we get:
cos 2α = 2 cos2 α − 1
Since the last two identities are direct descendants of the identity (O), we will list them
together.
For any angle α
cos 2α = cos2 α − sin2 α
(P)
cos 2α = 1 − 2 sin2 α
cos 2α = 2 cos2 α − 1
If we choose β = α in identity K, we get another double-angle identity.
sin(α + α) = sin α cos α + cos α sin α
That is,
For any angle α
sin 2α = 2 sin α cos α
(Q)
Identities listed as (P ) and (Q) are called double-angle identities.
Example. Suppose cos θ = 25 and sin θ < 0. Find the exact values of sin 2θ and cos 2θ.
Decide in what quadrant the terminal side lies when the angle 2θ is in standard position.
Answer. Since cos θ > 0 and sin θ < 0, when θ is in the standard position, the terminal
side is in the fourth quadrant. That is, 3π
< θ < 2π.
2
214
CHAPTER 11. APPLICATIONS: TRIGONOMETRIC IDENTITIES
O
P (2, b)
Let P (2, b) be a point on the terminal side of the angle θ, where b is a constant. Then by
the definition of cos θ, |OP | = 5. By the distance formula:
p
|OP | = (2 − 0)2 + (b − 0)2
√
=⇒ 5 = 22 + b2
=⇒ 25 = 4 + b2
=⇒ b2 = 21
√
=⇒ b = ± 21
√
√
Since P is a point in the fourth quadrant b = − 21. Therefore, sin θ = − 521 . Now by
using double-angle identities:
sin 2θ = 2 sin θ cos θ
√ ! 21
2
=2 −
5
5
√
4 21
=−
25
cos 2θ = cos2 θ − sin2 θ
√ !2
2
2
21
=
− −
5
5
4
21
−
25 25
17
=−
25
=
Since both cos 2θ and sin 2θ are negative, when the angle 2θ is in the standard position
their terminal side lies in the third quadrant.
11.4. HALF-ANGLE IDENTITIES
215
Exercise. Show that for any angle α, where tan α is defined,
tan 2α =
11.4
2 tan α
.
1 − tan2 α
(R)
Half-Angle Identities
In the last section we have discovered identities for cos 2α and sin 2α in terms of cos α
and sin α, for any given angle α. Similarly, we would like to obtain identities for cos α2
and sin α2 in terms of cos α and sin α, for any given angle α.
By using identity (P ), for any given angle α we get:
cos 2α = 2 cos2 α − 1
=⇒ 2 cos2 α = 1 + cos 2α
1 + cos 2α
=⇒ cos2 α =
2
Let θ = 2α. Then α = 2θ . Then the previous identity is:
1 + cos θ
θ
2
.
cos
=
2
2
By the Square-Root Principle Theorem,
For any angle θ,
r
θ
1 + cos θ
cos
=±
2
2
By using identity (P ) again, for any angle α we get:
cos 2α = 1 − 2 sin2 α
=⇒ 2 sin2 α = 1 − cos 2α
1 − cos 2α
=⇒ sin2 α =
2
(S)
216
CHAPTER 11. APPLICATIONS: TRIGONOMETRIC IDENTITIES
Let θ = 2α. Then α = 2θ . Then the previous identity is:
θ
1 − cos θ
sin
=
.
2
2
2
By the Square-Root Principle Theorem,
For any angle θ,
r
1 − cos θ
θ
=±
sin
2
2
Example. Find cos
standard position.
θ
2
and sin
(T)
θ
2
, if sin θ =
3
5
and cos θ < 0. Assume that θ is in
P (a, 3)
O
Answer. Since sin θ > 0 and cos θ < 0, the terminal side of θ is in the second quadrant.
Let P be the point on the terminal side of θ so that |OP | = 5. Then by the definition of
sin θ, the y-coordinate of P is 3. Assume that the x-coordinate of P is a. Then by the
Distance Formula Theorem,
5=
√
a2 + 3 2
=⇒ 25 = a2 + 9
=⇒ a2 = 16
=⇒ a = ±4
Since P is in the second quadrant, a = −4. Therefore, cos θ = − 45 .
11.5. PRODUCT-TO-SUM IDENTITIES
217
By using identity (S),
r
θ
1 + cos θ
cos
=±
2
2
s
1 + 54
=±
2
r
9
=±
10
Since π2 < θ < π, that is, θ is in the second quadrant,
first quadrant and cos 2θ = √310 .
π
4
<
θ
2
< π2 . Therefore,
θ
2
is in the
By using the identity (T ),
r
θ
1 − cos θ
sin
=±
2
2
s
1 − 54
=±
2
r
1
=±
10
Since
θ
2
is in the first quadrant, sin
θ
2
=
√1 .
10
Exercise. Show that for any angle θ, where cos θ 6= −1,
r
1 − cos θ
θ
=±
.
tan
2
1 + cos θ
11.5
Product-to-Sum Identities
Let us look at the super-star identities again.
(U)
218
CHAPTER 11. APPLICATIONS: TRIGONOMETRIC IDENTITIES
For any angle α and for any angle β,
cos(α − β) = cos α cos β + sin α sin β
(I)
cos(α + β) = cos α cos β − sin α sin β
(J)
sin(α + β) = sin α cos β + cos α sin β
(K)
sin(α − β) = sin α cos β − cos α sin β
(L)
If we subtract (J) from (I), we get,
cos(α − β) − cos(α + β) = 2 sin α sin β
That is,
For any angle α and for any angle β,
i
1h
sin α sin β = − cos(α + β) − cos(α − β)
2
(PTS 1)
If we add (I) and (J), we get,
cos(α − β) + cos(α + β) = 2 cos α sin β
That is,
For any angle α and for any angle β,
i
1h
cos α cos β =
cos(α + β) + cos(α − β)
2
If we subtract (L) from (K), we get,
sin(α + β) − sin(α − β) = 2 cos α sin β
That is,
(PTS 2)
11.6. SUM-TO-PRODUCT IDENTITIES
For any angle α and for any angle β,
i
1h
sin(α + β) − sin(α − β)
cos α sin β =
2
219
(PTS 3)
If we add (K) and (L), we get,
sin(α − β) + sin(α + β) = 2 sin α cos β
That is,
For any angle α and for any angle β,
i
1h
sin α cos β =
sin(α + β) + sin(α − β)
2
(PTS 4)
The identities PTS 1 - 4 are known as the Product-to-Sum Identities.
For any angle α and for any angle β,
i
1h
sin α sin β = − cos(α + β) − cos(α − β)
2
i
1h
cos α cos β =
cos(α + β) + cos(α − β)
2
i
1h
cos α sin β =
sin(α + β) − sin(α − β)
2
i
1h
sin α cos β =
sin(α + β) + sin(α − β)
2
11.6
Sum-to-Product Identities
Let A = α + β and B = α − β in identities PST 1 - 4.
If we add A and B, we get,
2α = A + B
(PTS 1)
(PTS 2)
(PTS 3)
(PTS 4)
220
CHAPTER 11. APPLICATIONS: TRIGONOMETRIC IDENTITIES
That is, α =
A+B
.
2
If we subtract B from A, we get,
2β = A − B
That is, β =
A−B
.
2
Now substitute A for α + β, B for α − β,
1 - 4. Then we get,
A+B
2
for α, and
A−B
2
for β in the identities PST
For any angle A and for any angle B,
sin
A+B
2
A+B
2
A+B
2
cos
sin
sin
A+B
2
cos
A−B
2
cos
sin
cos
=−
A−B
2
A−B
2
A−B
2
i
1h
cos A − cos B
2
i
1h
=
cos A + cos B
2
=
i
1h
sin A − sin B
2
=
i
1h
sin A + sin B
2
Multiply each identity by 2 and we get the four identities known as the Sum-to-Product
Identities.
11.7. OTHER TRIGONOMETRIC IDENTITIES AND APPLICATIONS
For any angle A and for any angle B,
A+B
A−B
cos A − cos B = 2 sin
sin
2
2
A+B
A−B
cos A + cos B = 2 cos
cos
2
2
A+B
A−B
sin A − sin B = 2 cos
sin
2
2
A−B
A+B
cos
sin A + sin B = 2 sin
2
2
221
(STP 1)
(STP 2)
(STP 3)
(STP 4)
If you can remember the identities PTS 1 - 4 and STP 1 - 4, then that is great. If you do
not want to remember these identities, then you should be able to derive them from the
four super-star identities as demonstrated. That is, if nothing else, you must remember
the super-stars.
11.7
Other Trigonometric Identities and
Applications
The trigonometric identities (A) - (U), PTS 1 - 4, and STP 1 - 4 are known as basic
trigonometric identities. You can derive or prove the validity of any other trigonometric
identity using the basic trigonometric identities, algebraic identities, along with some
basic algebraic methods such as using the distributive property and collecting like terms.
The reason why we can do this is ultimately related to the fact that every letter represents
a real number and the trigonometric numbers of an angle are real numbers.
For example, we can prove the following trigonometric identity using the difference of
squares identity and identities (D) and (M).
Example. Prove that, for any numbers A
cos4 A − sin4 A = cos 2A
Proof.
Left Side = cos4 A − sin4 A
222
CHAPTER 11. APPLICATIONS: TRIGONOMETRIC IDENTITIES
= (cos2 A − sin2 A)(cos2 A + sin2 A), by the difference of squares identity.
= (cos 2A) · (1), by identities (D) and (M).
= Right Side, for any number A.
Example. Prove that, for any numbers A and B,
sin(A + B) sin(A − B) = sin2 A − sin2 B
Proof.
Left Side = sin(A + B) sin(A − B)
= (sin A cos B + cos A sin B)(sin A cos B − cos A sin B),
by two of the super-stars
= sin2 A cos2 B − cos2 A sin2 B, by the difference of squares identity.
At this point of the proof we realize that there are no cosine terms on the right side.
Therefore, we could replace cos2 A by 1 − sin2 A, and cos2 B by 1 − sin2 B. With this
thought, let us go back to the proof of the identity.
Left Side = sin2 A cos2 B − cos2 A sin2 B
= sin2 A(1 − sin2 B) − (1 − sin2 A) sin2 B
= sin2 A − sin2 A sin2 B − sin2 B + sin2 A sin2 B, by the distributive property
= sin2 A − sin2 B, by collecting like terms.
= Right Side.
Exercise. Prove the identity in the above example by using the product-to-sum identities.
Exercise. Prove that cos 3θ = 4 cos3 θ − 3 cos θ.
[Hint: Write cos 3θ as cos(2θ + θ) and use the super-star identities.]
Exercise. Prove that sin 3θ = 3 sin θ − 4 sin3 θ.
Example. Find the exact value of sin 18◦ .
11.7. OTHER TRIGONOMETRIC IDENTITIES AND APPLICATIONS
π
Answer. 18◦ is 10
in radians. Let θ =
Now we will deploy the super-stars.
π
.
10
223
Then 5θ = π2 . Since cos π2 = 0, cos 5θ = 0.
cos 5θ = cos(3θ + 2θ)
= cos 3θ cos 2θ − sin 3θ sin 2θ
= (4 cos3 θ − 3 cos θ) cos 2θ − (3 sin θ − 4 sin3 θ) sin 2θ
= (4 cos3 θ − 3 cos θ)(cos2 θ − sin2 θ) − (3 sin θ − 4 sin3 θ)(2 sin θ cos θ)
= 4 cos5 θ − 4 cos3 θ sin2 θ − 3 cos3 θ + 3 cos θ sin2 θ − 6 sin2 θ cos θ + 8 sin4 θ cos θ
= cos θ(4 cos4 θ − 4 cos2 θ sin2 θ − 3 cos2 θ − 3 sin2 θ + 8 sin4 θ)
= cos θ(4 cos4 θ − 4 cos2 θ sin2 θ − 3(cos2 θ + sin2 θ) + 8 sin4 θ)
= cos θ(4 cos4 θ − 4 cos2 θ sin2 θ + 8 sin4 θ − 3)
Since cos 5θ = 0, we get:
cos θ(4 cos4 θ − 4 cos2 θ sin2 θ + 8 sin4 θ − 3) = 0
Since θ =
π
,
10
cos θ 6= 0. Therefore,
cos θ(4 cos4 θ − 4 cos2 θ sin2 θ + 8 sin4 θ − 3) = 0
=⇒ 4 cos4 θ − 4 cos2 θ sin2 θ + 8 sin4 θ − 3 = 0
Since we are interested in finding sin θ, we will use cos2 θ = 1 − sin2 θ to replace every
cos2 θ.
4 cos4 θ − 4 cos2 θ sin2 θ + 8 sin4 θ − 3 = 0
=⇒ 4(1 − sin2 θ)2 − 4(1 − sin2 θ) sin2 θ + 8 sin4 θ − 3 = 0
=⇒ 4 − 8 sin2 θ + 4 sin2 θ − 4 sin2 θ + 4 sin4 θ + 8 sin2 θ − 3 = 0
=⇒ 16 sin4 θ − 12 sin2 θ + 1 = 0
This is a quadratic equation in sin2 θ. The discriminant is 122 − 4(16)(1) = (16)(5).
Therefore, by the quadratic formula,
√
12 ± 4 5
2
sin θ =
32
√
3± 5
=
8
224
CHAPTER 11. APPLICATIONS: TRIGONOMETRIC IDENTITIES
Therefore
√
3± 5
8
s
sin θ = ±
Since θ is in the first quadrant,
s
√
1 3± 5
sin θ =
2
2
√
3+ 5
2
Clearly,
> 1. Therefore,
impossible since θ < π6 .
q
√
3+ 5
2
> 1. Then,
1
2
q
√
3+ 5
2
>
1
2
= sin π6 . But this is
Therefore,
s
1
sin θ =
2
√
3− 5
.
2
Example. Show that
1. cos π2 − α = sin α
2. sin π2 − α = cos α
Answer. By one of the super-stars,
π
π
π
− α = cos cos α + sin sin α
cos
2
2
2
= 0 · cos α + 1 · sin α
= sin α.
By another super-star,
π
π
π
sin
− α = sin cos α − cos sin α
2
2
2
= 1 · cos α − 0 · sin α
= cos α.
Exercise. Find the exact value of sin 18◦ by using the following method.
As before, let θ =
3θ =
π
− 2θ
2
π
.
10
Then 5θ =
π
2
or 3θ + 2θ = π2 . We can write this equation as
11.7. OTHER TRIGONOMETRIC IDENTITIES AND APPLICATIONS
225
Therefore,
cos 3θ = cos
π
− 2θ .
2
=⇒ 4 cos θ − 3 cos θ = sin 2θ
3
=⇒ 4 cos3 θ − 3 cos θ − sin 2θ = 0
=⇒ 4 cos3 θ − 3 cos θ − 2 sin θ cos θ = 0
=⇒ cos θ(4 cos2 θ − 3 − 2 sin θ) = 0
=⇒ 4 cos2 θ − 3 − 2 sin θ = 0
=⇒ 4(1 − sin2 θ) − 3 − 2 sin θ = 0
=⇒ 4 sin2 θ + 2 sin θ − 1 = 0
Now solve this quadratic equation in sin θ to find the exact value of sin θ. Compare your
answer to the answer obtained in the previous example.
Exercise. Find the exact value of cos 36◦ .
Exercise. Show that for any number θ,
cos3 θ − sin3 θ = (cos θ − sin θ)(1 + cos θ sin θ)
for all numbers θ.
Exercise. Show that for any number θ,
(cos θ + sin θ)2 = 1 + sin 2θ
for all numbers θ.
Example. Prove the following identity.
cos θ =
1 − tan2
1 + tan2
θ
2
θ
2
where θ is a real number.
Answer. The identity is invalid when θ = (2n + 1)π, for any integer n. Therefore, let us
assume otherwise.
Left Side = cos θ
= cos(2(θ/2))
226
CHAPTER 11. APPLICATIONS: TRIGONOMETRIC IDENTITIES
θ
θ
− sin2
2
2
2 θ
2 θ
cos 2 − sin 2
=
cos2 2θ + sin2 2θ
= cos2
=
1 − tan2 2θ
,
1 + tan2 2θ
θ
by dividing both the numerator and the denominator by cos2 .
2
Exercise. Prove the following identity.
2 tan 2θ
sin θ =
1 + tan2
where θ is a number.
θ
2
Chapter 12
Applications: Trigonometric
Equations
Earlier we obtained general solutions to simple trigonometric equations sin θ = a, cos θ =
a, and tan θ = a, where a is a number and −1 ≤ a ≤ 1, in the first two cases. The
following are those results.
General Solution to the Sine Equation Theorem.
Consider the equation sin x = a, where a is a real number.
1. If a > 1 or a < −1, then the equation has no solutions.
2. If −1 ≤ a ≤ 1, then the general solution of the equation is nπ + (−1)n sin−1 a,
where n is any integer.
General Solution to the Cosine Equation Theorem.
Consider the equation cos x = a, where a is a real number.
1. If a > 1 or a < −1, then the equation has no solutions.
2. If −1 ≤ a ≤ 1, then the general solution of the equation is 2nπ ± cos−1 a, where
n is any integer.
227
228
CHAPTER 12. APPLICATIONS: TRIGONOMETRIC EQUATIONS
General Solution to the Tangent Equation Theorem.
Consider the equation tan x = a, where a is a real number.
Then the general solution of the equation is nπ + tan−1 a, where n is any integer.
With the help of trigonometric and algebraic identities we can solve many more trigonometric equations. In this section we will look at some of those methods.
Example. Solve sin2 θ − 2 sin θ − 3 = 0.
Answer. Notice that this is a quadratic equation in sin θ. Assume that this equation is
true for some number θ. The left side of this equation can be factored into a product of
two linear factors of sin θ. That is,
(sin θ − 3)(sin θ + 1) = 0.
By the Zero Product Property Theorem, either sin θ − 3 = 0 or sin θ + 1 = 0. As a result,
we have two linear equations in sin θ. Namely, sin θ = 3 and sin θ = −1.
By the General Solution to the Sine Equation Theorem, the equation sin θ = 3 has no
solutions. By the same theorem, the general solution to the second equation sin θ = −1 is:
θ = nπ + (−1)n sin−1 (−1), where n is an integer.
π
n
= nπ + (−1) −
2
n π
= nπ − (−1)
2
If n is odd, then the general solution is θ = nπ + π2 and if n is even, then the general
solution is θ = nπ − π2 . In any of these cases, sin θ = −1. Therefore, by substituting −1
for sin θ in the given equation you can see that all these solutions check out.
Therefore, the general solution to the given equation is nπ − (−1)n π2 , where n is an
integer.
229
Example. Solve 2 cos2 θ − 1 = 0.
Answer. This is a quadratic equation in cos θ. By using the difference of squares identity,
we can factor the left side of this equation to obtain
√
√
( 2 cos θ − 1)( 2 cos θ + 1) = 0.
Then by the Zero Product Property Theorem, either
Therefore,
√
2 cos θ − 1 = 0 or
√
2 cos θ + 1 = 0.
1
1
cos θ = √ or cos θ = − √ .
2
2
By the General Theorem to the Cosine Equation Theorem, the general solution to the first
equation is:
1
−1
√ , where n is an integer.
θ = 2nπ ± cos
2
π
= 2nπ ± .
4
For any n, cos(2nπ ± π4 ) = cos(± π4 ) = √12 . By substituting √12 in the original equation,
you can see that the original equation is true for any of these numbers.
By the General Theorem to the Cosine Equation Theorem, the general solution to the
second equation is:
1
−1
θ = 2nπ ± cos
− √ , where n is an integer.
2
3π
.
= 2nπ ±
4
For any n, cos(2nπ± 3π
) = cos(± 3π
) = − √12 . By substituting − √12 in the original equation
4
4
you can see that the original equation is true for any of these numbers.
Therefore, the general solution to the given equation is:
2nπ ±
π
3π
or 2nπ ±
, where, n is an integer.
4
4
You can also solve the equation in the previous example if you recognize that the left side
of the equation is cos 2θ. This is because, cos 2θ = 2 cos2 θ − 1. Let us solve the previous
equation now using this identity.
230
CHAPTER 12. APPLICATIONS: TRIGONOMETRIC EQUATIONS
Example. Solve 2 cos2 θ − 1 = 0.
Answer. Assume the given equation is true for some number θ.
2 cos2 θ − 1 = 0
=⇒ cos 2θ = 0
=⇒ 2θ = 2nπ ± cos−1 0, where n is an integer.
π
=⇒ 2θ = 2nπ ±
2
π
=⇒ θ = nπ ±
4
If n is odd, then cos(nπ ± π4 ) = − √12 . The given equation is true for all those numbers. If
n is even, then cos(nπ ± π4 ) = √12 . Again, the given equation is true for all those numbers.
Therefore, the general solution of the given equation is nπ ± π4 , where n is an integer.
Exercise. Find particular solutions to the equation 2 cos2 θ − 1 = 0 in the interval [0, 2π],
first, using the general solution found in the first method, and second, using the general
solution found in the second method.
Based on our experience with solving algebraic equations, we know that we sometimes
get extraneous solutions. One instance, for example, was when we used the theorem: If
a = b then a2 = b2 , where a and b are real numbers.1 In the following example, we could
use this theorem. However, we will have to carefully check the solutions as some of the
solutions can be extraneous solutions.
Example. Find the general solution to the equation sin θ − cos θ = 1.
Answer (Method 1). Assume the given equation is true for some number θ.
If we square both sides of the equation, then
sin θ − cos θ = 1
=⇒ (sin θ − cos θ)2 = 1
=⇒ sin2 θ − 2 sin θ cos θ + cos2 θ = 1
=⇒ 1 − sin 2θ = 1
=⇒ sin 2θ = 0
1
See the section on solving radical equations for an example.
231
=⇒ 2θ = nπ + (−1)n sin−1 0, where n is an integer.
=⇒ 2θ = nπ
nπ
=⇒ θ =
2
nπ
2
If n = 4k + 1, where k is any integer, then sin
equation IS true.
If n = 4k − 1, where k is any integer, then sin
equation IS NOT true.
If n = 4k, where k is any integer, then sin
equation IS NOT true.
If n = 4k + 2, where k is any integer, then sin
equation IS true.
nπ
2
nπ
2
nπ
2
= 1 and cos
nπ
2
= −1 and cos
nπ
2
= 0 and cos
nπ
2
= 0 and cos
nπ
2
= 0, and the given
= 0, and the given
= 1, and the given
= −1, and the given
, where n is an integer of the
Therefore, the general solution of the given equation is nπ
2
form 4k + 1 or 4k + 2, where k is any integer. That is, all solutions of the given equation
can be written as 2kπ + π2 or 2kπ + π, where k is any integer.
The struggle to find the general solution of the equation of sin θ − cos θ = 1 as displayed
above leads us to seek a different method to find the general solution. One alternative
method of finding the general solution without “squaring both sides” is given below. The
plan is to use one of the super-star identities. We will develop the general method first
and then look at the previous example again.
Example. Find the general solution to the equation a sin θ − b cos θ = c, where a, b are
positive real numbers and c is a real number.
Answer. Assume the given equation is true for some number θ.
√
Divide both sides of the equation by a2 + b2 . Then the given equation becomes:
√
a
b
c
sin θ + √
cos θ = √
a2 + b2
a2 + b2
a2 + b2
First, notice that
a
√
2
a + b2
2
+
b
√
2
a + b2
2
=1
232
CHAPTER 12. APPLICATIONS: TRIGONOMETRIC EQUATIONS
Therefore, P √a2a+b2 , √a2b+b2 is a point on the unit circle. In addition, since both coordinates of P are positive, P is in the first quadrant. Then by the definitions of sine and
cosine numbers of an angle, there is an angle α in the first quadrant so that
cos α = √
a
b
and sin α = √
2
2
+b
a + b2
a2
Therefore, the given equation can be written as:
c
sin θ cos α − cos θ sin α = √
a2 + b 2
By using one of the super-star identities, we can write the above equation as:
sin(θ − α) = √
If −1 ≤
√ c
a2 +b2
c
a2 + b 2
≤ 1, then the above equation has solutions, and the general solution is:
n
θ − α = nπ + (−1) sin
−1
c
√
2
a + b2
, where n is any integer.
Therefore, the general solution to the given equation is:
c
n
−1
√
θ = nπ + (−1) sin
+ α.
a2 + b 2
Now we will use the method discovered in the previous example to find the general solution
of sin θ − cos θ = 1.
Example. Find the general solution to the equation sin θ − cos θ = 1.
Answer (Method 2). Assume the given equation is true for some number θ.
√
√
Divide both sides of the equation by 12 + 12 = 2. Then
sin θ − cos θ = 1
1
1
1
=⇒ √ sin θ − √ cos θ = √
2
2
2
π
π
1
=⇒ sin θ cos − cos θ sin = √
4
4
2
π
1
=⇒ sin θ −
=√
4
2
π
1
n
−1
√ , where n is an integer.
=⇒ θ − = nπ + (−1) sin
4
2
233
π
π
= nπ + (−1)n
4
4
π
nπ
=⇒ θ = nπ + (−1) +
4
4
=⇒ θ −
If n is even, that is n = 2k for some integer k, then θ = 2kπ + π2 and if n is odd, that is,
if n = 2k + 1 for some integer k, then θ = (2k + 1)π. By our previous work, we know that
both sets are solutions of the given equation. Therefore, the general solution of the given
equation is nπ + (−1)n π4 + π4 , where n is any integer.
√
Exercise. Find the general solution of sin θ + cos θ = 2, where θ is a real number.
Chapter 13
Applications: Circular Motion and
Simple Harmonic Motion
Consider a particle moving around a circle of radius r. We say the particle is in a circular
motion. Assume further that this particle moves at a constant speed . That is, the average
speed of the particle over any given time interval is constant. What does that mean
precisely? If t1 and t2 are the lengths of two arbitrary time intervals (in time units)
and s1 and s2 are the distance travelled by the particle (in distance units) in those time
intervals respectively, then st11 = st22 . Let us call this constant speed v “distance units per
time unit”. Then
s2
s
s1
=
= ,
v=
t1
t2
t
where s is the distance travelled in any given time interval t. In the case of circular motion,
s is the arc length of a sector of some central angle θ. If we use the radian measure for θ,
then by definition,
s = rθ
Therefore,
v=
rθ
t
Since v and r are constants, θt is a constant. We call this the constant angular speed of the
circular motion. We will use the Greek letter “omega” to represent the constant angular
speed.
ω=
θ
t
235
CHAPTER 13. APPLICATIONS: CIRCULAR MOTION AND SIMPLE HARMONIC
236
MOTION
Therefore, for a circular motion, the constant speed and the constant angular speed are
related by
v = rω
If we know either the constant speed or the constant angular speed, then we can calculate
the distance travelled and the angle travelled by the particle in a given period of time.
Example. Suppose a particle travels along a circle with radius 5 meters. Suppose the
constant speed of the particle is 2 meters/second. Find the constant angular speed of the
particle. Find how long it takes the particle to go around the circle once.
Answer. Since v = rω, 2 = 5ω. Therefore, the angular speed of the particle is
ans/second.
2
5
radi-
To go around the circle once, the particle must travel an angle of 2π. Suppose it takes t0
seconds for the particle to travel the angle of 2π. Then
θ
t
2
2π
=⇒
=
5
t0
π
=⇒ t0 =
5
Therefore, it takes
ω=
π
5
seconds for the particle to go around the circle once.
Introduce a coordinate system to the given circular motion so that the center of the circle
with radius r is the origin of the coordinate system. By the definition of sine and cosine
functions, the coordinates of the position of the moving particle, for a given angle θ, are
(r cos θ, r sin θ). That is, for a circular motion with constant angular speed of ω,
x = r cos ωt, and y = r sin ωt
Since r and ω are constants, both x and y depend only on time t, and therefore, both
x and y are functions of time. We indicate this by writing x and y using the functional
notation as follows.
x(t) = r cos ωt, and y(t) = r sin ωt
Now suppose a particle is allowed to move only along the y axis so that its motion is given
by
y = r sin ωt
237
Then we say the particle is in a simple harmonic motion. Then r is the amplitude of
is the period of the simple harmonic motion. The
the simple harmonic motion and 2π
ω
ω
quantity 2π is called the frequency of the simple harmonic motion.1
t=0
t=
π
2ω
t=
π
ω
t=
3π
2ω
t=
2π
ω
Instances of a spring in a simple harmonic motion
Exercise. Suppose a spring is in a simple harmonic motion given by y(t) = 3 sin 2t. Find
the amplitude, the period, and the frequency of this motion.
1
You will learn more details about simple harmonic motion when you take a course in the branch of
mathematics usually known as differential equations.
Chapter 14
An Introduction to Polar
Coordinates
Since high school you have been using a coordinate system known as the Cartesian coordinate system or the rectangular coordinate system. This system is designed to identify
any point on the plane by two numbers chosen as follows. Draw two number lines perpendicular to each other so that the point of intersection coincides with the point 0 on
each line. We identify one of the number lines as the first number line and the other as
the second number line. Usually the first number line is called the x-axis and is usually
shown as a horizontal line. The second number line is called the y-axis and is usually
shown as a vertical line. Let P be any arbitrary point on the plane. Drop a perpendicular
from P to the x-axis. Then this perpendicular will land on a number since the x-axis is
a number line. Let us call this number xp . Drop a perpendicular from P to the y-axis.
Suppose this perpendicular lands on the number yp . We will identify the point P using
the two numbers xp and yp in that order. Conventionally this ordered pair of numbers is
written as (xp , yp ). The number xp is called the x-coordinate of P and the number yp is
called the y-coordinate of P . We usually say the coordinates of P are (xp , yp ).
239
240
CHAPTER 14. AN INTRODUCTION TO POLAR COORDINATES
The following is another theorem that you may have learned in high school.
Theorem. Given a point P and a line ` on a plane, there is exactly one line passing
through P perpendicular to ` on the plane.
As a result of the above theorem, the coordinates of a point in the rectangular coordinate system are unique. Clearly, the coordinates of the origin (the point where the two
perpendicular number lines intersect) are (0, 0).
We have used the rectangular coordinate system to sketch the graph of a function f by
identifying the coordinates of all points (x, f (x)) and only those points on the plane. For
example, the graph of f (x) = sin x is the collection of all points (x, sin x) on the plane.
14.1
Polar Coordinate System
We will introduce another useful coordinate system known as the polar coordinate system
now. Once again consider a plane. Pick a point O on this plane. This fixed point O will
be called the pole from now on. Draw a ray so that the vertex of the ray is O. This fixed
ray will be called the polar axis from now on.
Polar Axis
O
Pole
Consider any arbitrary point P on the plane other than O. Let ` be the line passing
through O and P .1
1
Through two (distinct) points on the plane passes exactly one line.
14.1. POLAR COORDINATE SYSTEM
241
Polar Axis
Pole O
P
`
Let θ be an angle (in radians) whose initial side is the polar axis, whose vertex is O and
whose terminal side lies on `. As you can imagine, there are infinitely many choices to
pick an angle as described above. Let r be the length of the segment OP . Clearly, r is a
positive number. Let θ be a non-negative number. (The value of θ depends on the angle.)
We will assign an ordered pair of numbers to P as follows.
1. Suppose θ is measured counterclockwise and P lies on the terminal side of θ. Then
we assign (+r, +θ) to P .
θ
Polar Axis
Pole O
r
P (+r, +θ)
2. Suppose θ is measured clockwise and P lies on the terminal side of θ. Then we
assign (+r, −θ) to P .
242
CHAPTER 14. AN INTRODUCTION TO POLAR COORDINATES
Polar Axis
θ
Pole O
r
P (+r, −θ)
3. Suppose θ is measured counterclockwise and P does not lie on the terminal side of
θ. Then we assign (−r, +θ) to P .
θ
Polar Axis
Pole O
r
P (−r, +θ)
4. Suppose θ is measured clockwise and P does not lie on the terminal side of θ. Then
we assign (−r, +θ) to P .
Polar Axis
Pole O
θ
r
P (−r, −θ)
This system described so far leaves the point O on the plane with no assigned ordered
pair of numbers. Now we will assign an ordered pair of numbers to O. Suppose P = O.
Then there are infinitely many lines that pass through P and O. We can pick any one of
those lines to assign an ordered pair for O. Clearly, r = 0 and θ is arbitrary. Therefore,
14.2. POLAR EQUATIONS AND GRAPHS
243
we will assign (0, θ) for O, where θ is any arbitrary real number.
The system described above is known as the Polar Coordinate System of the plane. An
ordered pair (r, θ) for a given point P is called the polar coordinates of P .
14.2
Polar Equations and Graphs
A polar equation is an equation in r and θ. The following are a few examples of polar
equations.
r=1
π
θ=
4
r=θ
The graph of a polar equation is the collection of all solutions (r, θ) of the given equation.
We can sketch graphs of polar equations in polar coordinates by using few selected solutions and making an educated judgment of the placement of the rest of the solutions on
the plane as you probably did when you first looked at graphs of equations in x and y in
high school.
Example. Sketch the graph of r = 1.
Let us try to sketch the graph of the equation r = 1. We notice that there is no θ in this
equation. That means θ is arbitrary. That is, for any θ, (1, θ) is a solution of the given
equation. Let us select the radian measures of special angles for θ and make a table of selected solutions as you may have done in high school when you first leaned how to sketch a
r
θ
r
θ
1
π
2
1
0
graph of an equation. 1
π
6
1
1
π
4
1
π
3
r
r
θ
1
3π
2
1
5π
3
1
7π
4
1
11π
6
1
2π
θ
1
π
2π
3
1
7π
6
1
3π
4
1
5π
4
1
5π
6
1
4π
3
We will sketch these points on a plane using the polar coordinate system.
244
CHAPTER 14. AN INTRODUCTION TO POLAR COORDINATES
Now we can make an educated guess that the graph of the equation r = 1 is a circle with
center O and radius 1.
Example. Sketch the graph of θ = π4 .
We will make a table again. In this case, r is arbitrary. We will select a few positive
integer values, a few negative integer values, and 0 for r.
r
θ
0
π
4
1
π
4
2
π
4
3
π
4
r
θ
−1
π
4
−2
π
4
−3
π
4
14.2. POLAR EQUATIONS AND GRAPHS
We can see that the graph of the θ =
π
4
245
is a line passing through O with slope = 1.
Exercise. Sketch the graph of r = θ.
Example. Sketch the graph of r = cosθ.
Once again we will use the special angles to create a table of points and then sketch those
points to predict the graph of r = cosθ.
r
θ
1
0
√
3
2
π
6
√1
2
π
4
1
2
π
3
0
π
2
r
θ
− 12
2π
3
− √12
3π
4
√
−
3
2
−1
5π
6
π
246
CHAPTER 14. AN INTRODUCTION TO POLAR COORDINATES
It looks like the graph of r = cos θ is a circle with radius
of 12 from O on the polar axis.
14.3
1
2
and the center at a distance
Finding Relationships between Polar
Coordinates and Rectangular Coordinates
Let us introduce the rectangular coordinate system on the same plane with the polar
coordinate system as follows. We will select the origin of the rectangular coordinate
system as the pole O, we will select the x-axis so that the polar axis is on the x-axis, and
the y-axis passes though O.
y
Polar Axis
x
Pole O
Let P be an arbitrary point other than O on the plane. Suppose the rectangular coordinates of P are (x, y) and a polar coordinates of P are (r, θ). Then by the definitions of
14.3. RELATIONSHIPS BETWEEN POLAR AND RECTANGULAR
COORDINATES
247
cos θ and sin θ, cos θ = xr and sin θ = yr . Therefore, x = r cos θ and y = r sin θ. By the
p
sin θ
and since r 6= 0, we get, tan θ = xy .
distance formula, |OP | = x2 + y 2 . Since xy = rr cos
θ
These are the relationships that we sought.
x = r cos θ
y = r sin θ
p
r = ± x2 + y 2
y
tan θ =
x
Clearly, the rectangular coordinates of O are (0, 0) and r = 0, and θ is arbitrary at (0, 0).
y
x
(r, θ)
P
(x, y)
Example. Convert the equation r = 1 to rectangular coordinates.
p
Answer. In this equation, θ is arbitrary. Since r = ± x2 + y 2 , we can write r = 1 as
p
± x2 + y 2 = 1. This is the same as x2 + y 2 = 1.
Earlier we suspected the graph of r = 1 to be the circle with center O and radius 1. Since
the graph of x2 + y 2 = 1 is the unit circle, this confirms that our guess was correct.
Example. Convert the equation θ =
π
4
to rectangular coordinates.
Answer. In this equation r is arbitrary. Since tan π4 = 1, we can write θ = π4 as xy = 1,
If x 6= 0, then xy = 1 is the same as y = x. However, O is on the graph of r = tan π4
since (0, π4 ) are polar coordinates of O. Therefore by including the solution (0, 0) in the
existing set of solutions, we get y = x with no restrictions. Therefore, θ = π4 in rectangular
coordinates is y = x.
248
CHAPTER 14. AN INTRODUCTION TO POLAR COORDINATES
Earlier we suspected that the graph of θ = π4 to be the line passing though O with slope
1. Now we know that our guess was correct.
Example. Convert the equation r = cos θ to rectangular coordinates.
Answer. If we multiply both sides of the equation by r, then we get r2 = r cos θ. By using
conversion formulas, this equation becomes x2 + y 2 = x.
Earlier we suspected that the graph of r = cos θ to be the circle with the center 12 from
O on the polar axis and radius 21 . This suspicion should lead us to expect this graph
to be the same as the equation of a circle with center ( 12 , 0) and radius 12 in rectangular
coordinates. Is this prediction correct?
x2 + y 2 = x
=⇒ x2 − x + y 2 = 0
2
2
1
1
2
2
+y =
=⇒ x − x +
2
2
2
2
1
1
=⇒
x−
+ y2 =
2
2
This is indeed the equation of the circle with center ( 21 , 0) and radius 12 . (We used the
completing the square method in the above calculation.)
Exercise. Convert the equation r = cos θ to rectangular coordinates.
14.4
Selecting a Unique Pair of Polar Coordinates
for a Point
In contrast to the rectangular coordinates of a point, there are infinitely many polar
coordinates for a given point. It would be nice if we could select one pair of polar
coordinates as the standard polar coordinates of a point. By introducing restrictions to r
and θ, we can obtain a unique pair of polar coordinates for a point. First we introduce the
restriction r ≥ 0. That is, we will always select the angle so that P lies on the terminal
side of θ. In other words, we eliminate possibilities (3) and (4) in the description of the
polar coordinate system. (See the beginning of the section titled “The Polar Coordinate
System”.)
14.4. SELECTING A UNIQUE PAIR OF POLAR COORDINATES FOR A POINT249
Next we introduce the restriction θ ≥ 0. That is we will measure angles only in the counterclockwise direction. This eliminates possibility (2). The two restrictions introduced
thus far leave only the first option to select polar coordinates for a point. However, there
are still infinitely many ways to select polar coordinates for a given point P . The following
are two such possibilities.
Polar Axis
Pole O
Pole O
P (r, θ)
To eliminate all the infinitely many possible polar coordinates of P except one, we will
add another restriction: θ < 2π. With the following restrictions, any given point P will
have a unique ordered pair of polar coordinates.
r ≥ 0 and 0 ≤ θ < 2π.
With the above restrictions in place, we can state the relationships between rectangular
coordinates and polar coordinates as follows.
x = r cos θ
y = r sin θ
p
r = x2 + y 2
y
tan θ =
x
Under these new restrictions, however, the graph of θ =
through O with slope 1.
Exercise. What is the graph of θ =
π
4
π
4
is no longer a line passing
under the restrictions r ≥ 0 and 0 ≤ θ < 2π?
Chapter 15
An Introduction to Complex Plane
Consider a number line. Any point on this line is a real number. We will call this number
line “the real number line” or the “real axis”. Now imagine “rotating a number (a point
on the real axis) by π2 counterclockwise about 0”. We will indicate this rotation by i. Then
the notation 2i means “2 is rotated by π2 counterclockwise about 0”. Suppose we rotate
all real numbers this way. Then we will get a line perpendicular to the real axis at 0.
We will call this new axis the imaginary axis. Each point a on the real axis corresponds
to the point ai on the imaginary axis. In that sense the imaginary axis is a “number
line” with unit i. We will call these numbers imaginary numbers and we will call i the
imaginary unit. The real axis and the imaginary axis together define a plane.1 We will
call this plane the complex plane. The point on the complex plane where the real axis
and the imaginary axis meet is called the origin.
1
Recall that through any two distinct lines passes a unique plane.
251
252
CHAPTER 15. AN INTRODUCTION TO COMPLEX PLANE
Im
4i
3i
2i
1i
−4
−3
−2
−1
1
2
3
4
Re
−1i
−2i
−3i
−4i
We define imaginary number addition as follows.
ai + bi = (a + b)i
That is, ai + bi is the concatenation of imaginary segments ai and bi of lengths a and b
respectively.2
We define imaginary number multiplication as follows.
(ai)(bi) = (ab)ii
Notice that ii is “rotate i about the origin by π2 counterclockwise.” That is, ii is −1. We
denote this as i2 = −1. Also i2 i = (−1)i is −i, and we denote this as i3 = −i. Continuing
in this fashion, i4 = 1, i5 = i, and so on.
Multiplication of a real number a and i is defined as ai. That is a · i = ai. Therefore,
i = 1 · i.
2
This is analogous to the real number addition of a + b as the concatenation of segments of lengths
a and b respectively.
253
Now we define the addition of a real number and an imaginary number z = a + bi as
follows. Go to the real number a. That is, go to that point on the real axis. Then
from there rotate the real number b by pi2 counterclockwise about the point a. Then the
resulting point on the complex plane is called the complex number a + bi. In this fashion
we can identify each point on the complex plane by a complex number. Notice that both
a and b are real numbers. The real number a is called the real part of z and the real
number b is called the imaginary part of z.
Im
z = a + bi
bi
Re
a
The real numbers are the complex numbers of the form a + 0i and the imaginary numbers
are the complex numbers of the form 0 + bi. By this definition of a complex number
i = 0 + i, 1 = 1 + 0i and 0 = 0 + 0i.
We say two complex numbers z1 = a1 + b1 i and z2 = a2 + b2 i are equal if they are the
same point on the complex plane. That is, z1 = a1 + b1 i and z2 = a2 + b2 i are equal if
and only if a1 = a2 and b1 = b2 . If z = a + bi is a complex number, then z = 0 if and only
if both a = 0 and b = 0.
Since the collection of the real numbers is a subset of the complex numbers, we want
the complex numbers to have the same nice properties the real numbers have; namely,
associative properties, commutative properties (collecting like terms) and the distributive
property.
The addition of two complex numbers z1 = a1 + b1 i and z2 = a2 + b2 i denoted by z1 + z2
is
z1 + z2 = (a1 + a2 ) + (b1 + b2 )i.
254
CHAPTER 15. AN INTRODUCTION TO COMPLEX PLANE
The multiplication of the two complex numbers z1 = a1 + b1 i and z2 = a2 + b2 i denoted
by z1 z2 is
z1 z2 = (a1 a2 − b1 b2 ) + (a1 b2 + b1 a2 )i.
You should be able to verify this using the distributive property, collecting like terms and
using i2 = −1.
The subtraction of z2 from z1 is denoted by z1 − z2 and it is
z1 − z2 = (a1 − a2 ) − (b1 − b2 )i.
Suppose z = a + bi 6= 0. We will define z1 as the complex number so that z · z1 = 1. You
can see that (a + bi)(a − bi) = a2 + b2 . The number a − bi denoted by z is called the
complex conjugate of z. Then zz is the real number a2 + b2 . Since z 6= 0, a2 + b2 6= 0.
2 +b2
2
Therefore, we know that aa2 +b
2 = 1. If we denote zz as |z| , then
a
b
1
= 2 − 2 i.
z
|z|
|z|
We will denote
a
|z|2
−
b
i
|z|2
as
z
.
|z|2
Then
1
z
= 2.
z
|z|
Now we can define the division of complex numbers. Suppose z1 = a1 +b1 i and z2 = a2 +b2 i
are two complex numbers so that z2 6= 0. Then
z1 z2
z1
=
.
z2
|z2 |2
In other words,
z1
a1 a2 + b 1 b 2
a1 b 2 − b 1 a2
=
−
i.
z2
a22 + b22
a22 + b22
Exercise. Verify the above assertion.
15.1
Polar Form of a Complex Number
Let us introduce a polar coordinate system in the complex plane by choosing the point
0 + 0i as the pole and the positive real axis as the polar axis. Consider an arbitrary
15.2. MULTIPLICATION OF COMPLEX NUMBERS IN POLAR FORM
255
complex number z = a + bi. Let (r, θ) be the polar coordinates of z as seen as a point
with rectangular coordinates (a, b). We will introduce the standard restrictions on r and
θ, that is r ≥ 0 and 0 ≤ θ < 2π, to make the polar coordinates of z unique. Then
r=
√
a2 + b2 , a = r cos θ, and b = r sin θ.
Therefore, z can be written as
z = r(cosθ + i sin θ), where, r ≥ 0 and 0 ≤ θ < 2π.
This is known as the standard polar form of a complex number. The number r is called the
modulus of the complex number and the number θ is called the argument of the complex
number. Notice that modulus of z is |z|. We abbreviate the modulus of z as “mod z” and
the argument of z as “arg z”.
Example. Write z = 2 − 2i in standard polar form.
p
√
√
√
Answer. r = 22 + (−2)2 = 2 2. Therefore, 2 2 cos θ = 2, and 2 2 sin θ = −2. Since
√
sin θ < 0 and cos θ > 0, the angle θ is in the fourth quadrant. 2 2 cos θ = 2 implies that
cos θ = √12 and sin θ = − √12 . Therefore, θ = 7π
, and the polar form of the given complex
4
number is
√
7π
7π
z = 2 2 cos
+ i sin
.
4
4
15.2
Multiplication of complex numbers in Polar
Form
Let z1 = r1 (cos θ1 + i sin θ1 ) and z2 = r2 (cos θ2 + i sin θ2 ) be two complex numbers in
standard polar form. Then
z1 z2 = (r1 (cos θ1 + i sin θ1 )(r2 (cos θ2 + i sin θ2 ))
= r1 r2 (cos θ1 + i sin θ1 )(cos θ2 + i sin θ2 )
= r1 r2 (cos θ1 cos θ2 − sin θ1 sin θ2 ) + i(sin θ1 cos θ2 + cos θ1 sin θ2 )
= r1 r2 (cos(θ1 + θ2 ) + i sin(θ1 + θ2 ))
Therefore, the modulus of z1 z2 is the product of the moduli and the argument of z1 z2 is
the sum of the arguments. We summarize our findings in the following theorem.
256
CHAPTER 15. AN INTRODUCTION TO COMPLEX PLANE
Complex Number Multiplication Theorem. If z1 = r1 (cos θ1 + i sin θ1 ) and z2 =
r2 (cos θ2 + i sin θ2 ) are two complex numbers, then z1 z2 = r1 r2 (cos(θ1 + θ2 ) + i sin(θ1 +
θ2 )).
Example. Let z1 = (cos 11π
+i sin 11π
) and z2 = (cos 3π
+i sin 3π
) be two complex numbers.
6
6
4
4
Find z1 z2 and write it in standard polar form.
Answer. In this problem the mod z1 is 1 and mod z2 is also 1. Therefore, the product of
and arg z1 is 3π
. Therefore the sum of the arguments is
the modules is 1. The arg z1 is 11π
6
4
11π
3π
31π
+ 4 . That is, the sum of the arguments is 12 . However, 31π
> 2π. So we choose the
6
12
31π
angle in 0 ≤ θ < 2π which has the same terminal side of 12 . That is, θ = 7π
. Therefore,
12
7π
7π
the standard polar form of z1 z2 is cos 12 + i sin 12 .
15.3
Division of complex numbers in Polar Form
Let z1 = r1 (cos θ1 + i sin θ1 ) and z2 = r2 (cos θ2 + i sin θ2 ) be two complex numbers in
standard polar form. Then
z1
z1 z2
=
z2
|z2 |2
(r1 (cos θ1 + i sin θ1 )(r2 (cos θ2 − i sin θ2 ))
=
r22 (cos2 θ2 + sin2 θ2 )
r1
= (cos θ1 + i sin θ1 )(cos θ2 − i sin θ2 )
r2
r1
= (cos θ1 cos θ2 + sin θ1 sin θ2 ) + i(sin θ1 cos θ2 − cos θ1 sin θ2 )
r2
r1
= (cos(θ1 − θ2 ) + i sin(θ1 − θ2 ))
r2
Therefore, the modulus of zz12 is the quotient of the moduli and the argument of zz12 is the
difference of the arguments. We summarize our findings in the following theorem.
Complex Number Division Theorem. If z1 = r1 (cos θ1 + i sin θ1 ) and z2 =
r2 (cos θ2 + i sin θ2 ) are two complex numbers, then zz21 = rr12 (cos(θ1 − θ2 ) + i sin(θ1 − θ2 )).
15.4. INTEGER POWERS OF COMPLEX NUMBERS IN POLAR FORM
257
Example. Let z1 = (cos π6 + i sin π6 ) and z2 = (cos 3π
+ i sin 3π
) be two complex numbers.
4
4
Find z1 z2 and write it in the standard polar form.
Answer. In this problem the mod z1 is 1 and mod z2 is also 1. Therefore, the quotient
. Therefore the difference of the
of the modules is 1. The arg z1 is π6 and arg z1 is 3π
4
π
3π
7
arguments is 6 − 4 . That is, the difference of the arguments is − 12
. However, − 7π
> 2π.
12
So we choose the angle in 0 ≤ θ < 2π which has the same terminal side of − 7π
. That is,
12
z1
17π
17π
17π
θ = 12 . Therefore, the standard polar form of z2 is cos 12 + i sin 12 .
15.4
Integer Powers of complex numbers in Polar
Form
The integer power of a complex number can be found using a useful theorem known as
De Moivre’s Theorem. Before proving De Moivre’s Theorem, we need two definitions. If
z is a complex number and n is an integer, then
z 0 = 1 and z −n =
1
.
zn
De Moivre’s Theorem. If θ is a real number and n is an integer, then (cos θ +
i sin θ)n = cos nθ + i sin nθ.
Proof. We will prove this theorem in three cases, by using the trichotomy Law of real
numbers: since n is an integer, n > 0, n = 0, or n < 0.
Case 1: Suppose n > 0.
We will prove this case using mathematical induction.
First step: Show that (cos θ + i sin θ)1 = cos 1θ + i sin 1θ. But this is obviously true.
Inductive step: Suppose the given statement is true for some arbitrary positive
integer k ≥ 1. That is, we assume that
(cos θ + i sin θ)k = cos kθ + i sin kθ is true.
(1)
We have to show that the given statement is true for k + 1. That is, we have to
show that
(cos θ + i sin θ)k+1 = cos(k + 1)θ + i sin(k + 1)θ is also true.
(2)
258
CHAPTER 15. AN INTRODUCTION TO COMPLEX PLANE
Left side of (2) = (cos θ + i sin θ)k+1
= (cos θ + i sin θ)k (cos θ + i sin θ)
= (cos kθ + i sin kθ)(cos θ + i sin θ), by (1).
= cos(kθ + θ) + i sin(kθ + θ),
by the Complex Number Multiplication Theorem.
= cos(k + 1)θ + i sin(k + 1)θ
= Right side of (2).
Therefore, by mathematical induction, the given statement is true for any positive
integer n.
Case 2: Suppose n = 0.
We have to show that (cos θ + i sin θ)0 = cos 0θ + i sin 0θ.
The left side is 1, by definition, and the right side is 1 + 0i = 1. Therefore, the given
statement is true for n = 0.
Case 3: Suppose n < 0.
Let n = −m. Then m is a positive integer.
(cos θ + i sin θ)n = (cos θ + i sin θ)−m
1
=
(cos θ + i sin θ)m
1
=
, by Case 1 of this theorem.
cos mθ + i sin mθ
cos mθ − i sin mθ
=
(cos mθ + i sin mθ)(cos mθ − i sin mθ)
cos mθ − i sin mθ
=
cos2 mθ + sin2 mθ
cos mθ − i sin mθ
=
1
= cos(−mθ) + i sin(−mθ)
= cos(−m)θ + i sin(−m)θ
= cos nθ + i sin nθ
Example. Let z1 = 2(cos 5π
+ i sin 5π
). Find (z1 )10 and write it in the standard polar
6
6
form.
15.5. DISTINCT COMPLEX nTH ROOTS OF A COMPLEX NUMBER IN POLAR
FORM
259
Answer.
10
5π
5π
10
+ i sin
z1 = 2 cos
6
6
10
5π
5π
10
cos
=2
+ i sin
6
6
50π
50π
10
cos
+ i sin
, by De Moivre’s Theorem.
=2
6
6
2π
2π
10
cos 8π +
=2
+ i sin 8π +
6
6
π
π
= 210 cos + i sin
.
3
3
15.5
Distinct Complex nth roots of a Complex
Number in Polar Form
In the eighth grade you may have learned the definition of the nth root of a positive real
number: if a is a positive real number, then the real number b is called the nth root of a
if bn = a, where n is a positive integer. We will define the nth root of a complex number
the same way. If z is a complex number then we say the complex number w is a complex
nth root of z if wn = z, where n is a positive integer.
Let z = r(cos θ + i sin θ) be a complex number so that 0 ≤ θ < 2π. Then clearly,
w = r1/n (cos nθ + i sin nθ ) is a complex nth root of z. (You can verify this by using De
Moivre’s Theorem and the definition of the complex nth root.)
For k ≥ 0, 2kπ+θ < 2(k+1)π, since θ < 2π. We also know that r(cos(2kπ+θ)+i sin(2kπ+
θ)) = r(cos θ + i sin θ) = z. Therefore, for k ≥ 0, all wk = r1/n (cos( 2kπ+θ
) + i sin( 2kπ+θ
))
n
n
2kπ+θ
are complex nth roots of z, where n > 2. If n < 2π for some values of k, then those
wk ’s are distinct complex numbers in standard polar form. Therefore, it is possible for z
to have many distinct complex nth roots for n > 2, provided 2kπ+θ
< 2π.
n
2kπ + θ
< 2π =⇒ 2kπ + θ < 2nπ
n
=⇒ 2kπ < 2nπ − θ
θ
=⇒ k < n −
2π
=⇒ k ≤ n − 1 since k ≥ 0 and n > 0 are integers and θ < 2π.
260
CHAPTER 15. AN INTRODUCTION TO COMPLEX PLANE
Therefore, wk = r1/n (cos( 2kπ+θ
) + i sin( 2kπ+θ
)) are distinct complex nth roots of z for all
n
n
0 ≤ k ≤ n − 1. We will summarize our findings in the following theorem.
Complex nth Roots Theorem. Let z = r(cos θ + i sin θ) be a complex number in
standard polar form. Then for a positive integer n > 0, the distinct complex nth roots
) + i sin( 2kπ+θ
)), for all integers k, 0 ≤ k ≤ n − 1.
of z are wk = r1/n (cos( 2kπ+θ
n
n
Example. Find all distinct complex 3rd roots of 1.
Answer. We can write 1 in standard polar form as follows.
1 = 1 + 0i = cos 0 + i sin 0
Now we can find the distinct complex 3th roots of z = cos 0 + i sin 0 by using the Complex
nth Roots Theorem. The modulus of z is 1 and 11/3 = 1. Since n = 3, 0 ≤ k ≤ 2. Then,
0+0
0+0
w0 = 1(cos
+ i sin
) = cos 0 + i sin 0 = 1
3
3 2π + 0
2π + 0
2π
2π
w1 = 1 cos
+ i sin
+ i sin
= cos
3
3
3
3
4π + 0
4π + 0
4π
4π
w2 = 1 cos
+ i sin
+ i sin
= cos
3
3
3
3
+ i sin 2π
, and cos 4π
+ i sin 4π
.
Therefore, the distinct complex 3rd roots of 1 are 1, cos 2π
3
3
3
3
2π
2π 3
4π
4π 3
As an exercise, show that (cos 3 + i sin 3 ) = 1 and (cos 3 + i sin 3 ) = 1.
A complex equation is an equation containing complex numbers.
Example. Find the distinct solutions of the complex equation z 4 − 2 = 0.
Answer. Assume the given equation is true for some complex number z. Then
z4 = 2
= 2(1 + 0i)
= 2(cos 0 + i sin 0)
Now we can find the distinct complex 4th roots of z1 = 2(cos 0 + i sin 0) by using the
Complex nth Roots Theorem. The modulus of z1 is 2, the modulus of any 4th root is 21/4 .
Since n = 4, 0 ≤ k ≤ 3. Then,
0+0
0+0
+ i sin
) = 21/4 (cos 0 + i sin 0) = 21/4
w0 = 21/4 (cos
4
4
15.5. DISTINCT COMPLEX nTH ROOTS OF A COMPLEX NUMBER IN POLAR
FORM
261
2π + 0
2π + 0
π
π
w1 = 21/4 cos
+ i sin
= 21/4 cos + i sin
4
4
2
2
4π + 0
4π + 0
+ i sin
= 21/4 (cos π + i sin π)
w2 = 21/4 cos
4
4
6π + 0
6π + 0
3π
3π
1/4
1/4
w3 = 2
cos
+ i sin
=2
cos
+ i sin
4
4
2
2
Therefore, the distinct solutions of the given equation are 21/4 , 21/4 cos π2 + i sin π2 , 21/4 (cos π + i sin π),
3π
and 21/4 cos 3π
+
i
sin
. You can use De Moivre’s Theorem to verify that these are ac2
2
tually solutions of the given equation.
Example. Find the distinct solutions of the complex equation z 3 − i = 0.
Answer. Assume the given equation is true for some complex number z. Then
z3 = i
= 0 + 1i
π
π
= cos + i sin
2
2
Now we can find the distinct complex 3th roots of z1 = cos π2 + i sin π2 by using the Complex
nth Roots Theorem. Then,
0 + π2
0 + π2
π
π
w0 = cos
+ i sin
= cos + i sin
4
4
8
8
π
π 2π + 2
2π + 2
5π
5π
w1 = cos
+ i sin
+ i sin
= cos
4
4
8
8
π π
4π + 2
4π + 2
9π
9π
w2 = cos
+ i sin
= cos
+ i sin
4
4
8
8
Therefore, the distinct solutions of the given equation are cos π8 + i sin π8 , cos 5π
+ i sin 5π
,
8
8
9π
9π
and cos 8 + i sin 8 .
Exercise. Solve the equation z 3 = 2 − 2i.
Chapter 16
An Introduction to Vectors
A certain physical quantity with two properties, namely, a magnitude and a direction,
is called a vector . Examples of such physical quantities are the constant velocity (of a
particle moving along a straight line), the constant acceleration (of a particle moving
along a straight line), and the weight (of an object on the surface of the Earth). A certain
physical quantity with only one property is called a scalar . Examples of scalars are the
mass of a particle and the length of a segment.
Geometrically, we will use an arrow with a fixed length to represent a vector.
B
u
A
The point with the arrowhead is called the terminal point of the vector and the point at
the other end of the arrow is called the initial point of the vector. If we name the initial
point A and the terminal point B, then we use the notation AB to represent the vector.
We will also use small English letters with an over-line to name vectors. For example,
we may use u or v to name vectors. (As you may know, we always use small English
263
264
CHAPTER 16. AN INTRODUCTION TO VECTORS
letters for numbers.) The direction of a vector AB is defined by a pair of points: the
initial point and the terminal point of AB. If you can imagine going from the initial point
A of a vector AB to the terminal point B of AB along the line segment AB, then you
are traveling in the direction of the vector AB. We define the magnitude (or norm) of a
vector AB as the length of the segment AB. We denote the norm of a vector u by the
notation kuk.
We define a zero vector denoted by 0 as the vector with norm 0. That is, for a zero vector,
the initial point and the terminal point are the same. In other wards, AA is a zero vector.
We let the zero vector to have any direction it would like to have. In other words, the
direction of 0 is arbitrary.
Let AB and CD be two vectors. We say AB and CD have the same norm if kABk =
kCDk.
−→
Let AB be the ray with initial point A that contains the vector AB.
We say AB and CD have the same direction if one of the following conditions holds.
−→
−−→
1. Suppose AB and CD lie on the same line. If either AB contains CD completely or
−−→
−→
CD contains AB completely, then we say AB and CD have the same direction.
2. Suppose AB and CD do not lie on the same line. If ABDC is a trapezoid with
ABkCD then we say AB and CD have the same direction.
D
B
B
D
C
A
A
C
We say AB and CD have the opposite direction if one of the following conditions holds.
−→
−−→
1. Suppose AB and CD lie on the same line. If neither AB contains CD completely nor
−−→
−→
CD contains AB completely, then we say AB and CD have the opposite direction.
16.1. VECTOR ADDITION
265
2. Suppose AB and CD do not lie on the same line. If ABCD is a trapezoid with
ABkDC then we say AB and CD have the opposite direction.
C
B
C
D
B
A
D
A
We say u = v if u and v have the same norm and the same direction. The “two” vectors
in the following figure are the same. In other words, we can move a vector as long as we
do not change any of the two properties of the vector, namely, the norm and the direction.
v
v
16.1
Vector Addition
Let u and v be vectors. We define u + v as follows. Move the vector v so that its initial
point coincides with the terminal point of u. The vector with the initial point the same as
the initial point of u and the terminal point the same as the terminal point of v is called
u + v.
266
CHAPTER 16. AN INTRODUCTION TO VECTORS
v
u+v
u
v
Question. We know that the real numbers satisfy the commutative property of addition.
That is, if a and b are real numbers, then a + b = b + a. Is vector addition commutative?
That is, if u and v are vectors, then is u + v = v + v?
Answer. If u or v is 0, then you can easily show that u+v = v +u, by using the definition
of the vector addition. This is left as an exercise.
Assume u 6= 0 and v 6= 0. We can find u + v and v + u according to the definition. Let
the initial point of u + v be A, the terminal point of u + v be B, the initial point of v + u
be C, and the terminal of v + u be D. We want to show that u + v = v + u. That is, we
have to show that u + v and v + u have the same norm and the same direction.
D
u
v+u
v
B
C
u
u+v
A
You may have learned the following theorem in high school.
The Parallelogram Theorem. A quadrilateral is a parallelogram if and only if a
pair of opposite sides are parallel and have the same length.
16.2. SCALAR MULTIPLICATION OF A VECTOR
267
ABDC is a parallelogram because AC = BD and ACkBD by the above theorem. Then
by the same theorem, AB = CD and ABkCD. Therefore, u + v = v + u.
16.2
Scalar Multiplication of a Vector
Suppose u is a vector and k is a scalar.
1. If u 6= 0 and k > 0, then ku is the vector with norm kkuk and the direction same
as u.
2. If u 6= 0 and k < 0, then ku is the vector with norm |k|kuk and the direction
opposite to u.
3. If either u = 0 or k = 0, then ku = 0.
u
u
1
u
2
− 12 u
Definition.
Let u and v be two vectors.
1. −u = (−1)u
2. u − v = u + (−1)v
A vector u is called a unit vector if kuk = 1.
Theorem. If u is a non-zero vector given by u = hu1 , u2 i, then
1
u
kuk
is a unit vector.
Proof. Since kuk 6= 0, by the definition of the norm of a vector, kuk > 0. Since kuk is a
1
1
1
positive scalar, kuk
is a positive scalar. The norm of the vector kuk
u is equal to kuk
kuk,
268
CHAPTER 16. AN INTRODUCTION TO VECTORS
by the definition of scalar multiplication. Therefore, the norm of the vector
the cancellation law of the real numbers).
1
u
kuk
is 1, (by
Exercise. If u is a non-zero vector, then show that
1
kuk
u = u.
kuk
With the above exercise done, we are in a position to give meaning to the second property
of a non-zero vector u, namely the “direction”. Since a vector u has only two properties
1
and kuk is the norm, then kuk
u must represent the “direction” of the vector.
16.3
Algebraic Representation of a Vector
Let u be a vector. Introduce a rectangular coordinate system to the plane. Let O be the
origin of this coordinate system. Move u so that the initial point of u is O. Let P (u1 , u2 )
be the coordinates of the terminal point of u. Since the coordinates of P are unique, we
can use the coordinates of P to give an algebraic representation of u.
u = hu1 , u2 i
We want to use this new notation for vectors to distinguish the vector u from the point
P (u1 , u2 ). The new notation is known as “bra-ket” notation or “langle-rangle” notation.1
y
(u1 , u2 )
u
O
x
Now we can give an algebraic representation to the norm of a vector. Let u = hu1 , u2 i be
a given non-zero vector. Then by the distance formula,
q
kuk = u21 + u22 .
1
Paul Dirac introduced the bra-ket notation in the 1920’s while discovering the principles of quantum
physics and Donald Knuth introduced langle-rangle — which stands for left angle and right angle —
when he created the TEX Typesetting System in the 1980’s.
16.3. ALGEBRAIC REPRESENTATION OF A VECTOR
Recall that the unit vector
1
u
kuk
269
gives the direction of a non-zero vector u. Therefore,
1
1
hu1 , u2 i.
u= p 2
kuk
u1 + u22
We define the unit vector i = h1, 0i to be the direction of any vector whose initial point
is O and whose terminal point is on the positive x-axis.
y
i
x
1
O
Exercise. Let u = h3, 0i. Show that u = 3i.
y
u
3
O
x
Exercise. Let v = h−3, 0i. Show that v = −3i.
y
v
−3
O
x
We define the unit vector j = h0, 1i as the direction of any vector whose initial point is
O and whose terminal point is on the positive y-axis.
270
CHAPTER 16. AN INTRODUCTION TO VECTORS
y
1
j
x
O
Exercise. Let u = h0, 3i. Show that u = 3j.
y
3
u
x
O
Exercise. Let v = h0, −3i. Show that v = −3j.
y
x
O
v
−3
Theorem. Suppose u = hu1 , u2 i is a vector. Then u = u1 i + u2 j.
16.3. ALGEBRAIC REPRESENTATION OF A VECTOR
271
Exercise. Prove the above theorem.
Vector Addition Theorem. Suppose u = hu1 , u2 i and v = hv1 , v2 i are vectors.
Then u + v = hu1 + v1 , u2 + v2 i.
Proof. By the Trichotomy Law, u1 > 0, u1 = 0, or u1 < 0. The same is true for u2 , v1 ,
and v2 . If we look at all combinations of the above possibilities, there are 34 = 81 cases
to consider. If u = 0 or v = 0, then the proof is obvious from the definition of the vector
addition. Therefore, we will assume that both u and v are non-zero vectors. That still
leaves 64 cases to consider. We will prove the theorem for the case u1 > 0, u2 > 0, v1 > 0,
and v2 > 0. The methods and tools we use to prove this case can be used to prove all
other cases.
If u and v have the same direction, then the proof is not difficult and will be left as an
exercise. Therefore, assume that the directions of u and v are different.
H
v
C
A
u+v
u
v
O
G
D
B
E
F
Let u = OA and v = OB. Let OC be the moved v. Then u + v = OC. We have to show
that the coordinates of C are (u1 + v1 , u2 + v2 ). (Without loss of generality, assume that
u and v are the vectors as shown on the figure.)
Drop a perpendicular from A to the x-axis and let the foot of this perpendicular be D.
Drop a perpendicular from B to the x-axis and let the foot of this perpendicular be E.
Drop a perpendicular from C to the x-axis and let the foot of this perpendicular be F .
272
CHAPTER 16. AN INTRODUCTION TO VECTORS
Drop a perpendicular from A to the line CF and let the foot of this perpendicular be G.
−→
Let H be a point on the ray OA as shown in the figure.
OBkAC and OA is a transversal. Therefore, |∠AOB| = |∠HAC|. (Corresponding
angles.) Since both OF and AG are perpendicular to CF , OF kAG. The line OA is
a transversal to the parallel lines OF and AG. Therefore, |∠AOE| = |∠HAG|. Then
|∠BOE| = |∠CAG|, because |∠BOE| = |∠AOE| − |∠AOB| = |∠HAG| − |∠HAC| =
|∠CAG|.
By the ASA theorem, triangle 4OBE is congruent to the triangle 4ACG. Therefore,
|AG| = |OE| = v1 , and |CG| = |BE| = v2 .
Since ADF G is a rectangle, |GF | = |AD| = u1 , and |DF | = |AG| = v1 .
Now, |OF | = |OD| + |DF | = u1 + v1 and |CF | = |GF | + |CG| = u2 + v2 . Therefore, the
coordinates of C are (u1 + v1 , u2 + v2 ).
Scalar Multiplication Theorem. Suppose u = hu1 , u2 i is a vector and k is a scalar.
Then ku = hku1 , ku2 i.
Proof. By the Trichotomy Law, there are 33 = 27 possible combinations of k, u1 and
u2 . If k = 0 or u = 0, then proof follows immediately from the definition of the scalar
multiplication. That eliminates 6 cases. We will consider the case k > 0, u1 > 0, u2 > 0.
Tools and the methods used to prove the theorem in this case can be used to prove the
theorem in all other cases.
Within this case, there are three cases. k < 1, k > 1 or k = 1. The proof of the case
k < 1 is similar to the proof of the case k > 1. Therefore, we will prove the theorem for
the following case. k ≥ 1, u1 > 0, and u2 > 0.
If k = 1, then the proof follows immediately from the definition. That is, by the definition
of the scalar multiplication,
1u = u
Therefore,
1hu1 , u2 i = hu1 , u2 i = h1u1 , 1u2 i.
16.3. ALGEBRAIC REPRESENTATION OF A VECTOR
273
Now suppose k > 1.
ku B
u
O
A
C
D
Let u = OA and ku = OB. We want to show that the coordinates of B are (ku1 , ku2 ).
Drop a perpendicular from A to the x-axis and let the foot of this perpendicular be C.
Drop a perpendicular from B to the x-axis and let the foot of this perpendicular be D.
By the AA criterion, the triangles 4OAC and 4OBD are similar. Therefore,
|OD|
|OB|
=
.
|OC|
|OA|
Therefore, by the cross-multiplication algorithm,
|OB|
kkuk
|OD| = |OC| ·
= u1
= ku1 .
|OA|
kuk
Also,
|OB|
|BD|
=
.
|AC|
|OA|
Therefore, by the cross-multiplication algorithm,
|OB|
kkuk
= u2
= ku2 .
|BD| = |AC| ·
|OA|
kuk
Therefore, the coordinates of B are (ku1 , ku2 ).
The following theorem follows easily from the Vector Addition Theorem and the Scalar
Multiplication Theorem. The proof is left as an exercise.
274
CHAPTER 16. AN INTRODUCTION TO VECTORS
Properties of Vectors Theorem. Suppose u = hu1 , u2 i, v = hv1 , v2 i, w = hw1 , w2 i
are vectors, k, k1 , and k2 are scalars. Then
1.
2.
3.
4.
5.
u+v =v+u
u + (v + w) = (v + u) + w
k1 (k2 u) = (k1 k2 )u
0u = 0
0+u=u
Exercise. Prove the Properties of Vectors Theorem.
16.4
Dot Product Between Two Vectors
Let u = hu1 , u2 i and v = hv1 , v2 i be two vectors. We define the dot product between u
and v, denoted by u · v, as follows.
u · v = u1 v1 + u2 v2 .
The above definition is purely an algebraic definition. Does it have a geometrical meaning?
To find out we will investigate the information we can obtain from the above definition.
16.4.1
Properties of the Dot Product
(P1) By definition, the dot product between two given vectors is a scalar. If one of the
two vectors is the zero vector, then the dot product is 0.
(P2) The dot product is commutative. That is,
u·v =v·u
Proof.
u · v = u1 v1 + u2 v2 , by definition.
v · u = v1 u1 + v2 u2 , also by definition.
u · v = v · u, since numbers commute.
16.4. DOT PRODUCT BETWEEN TWO VECTORS
275
(P3) Following the same line of thinking and using the Vector Addition Theorem, you
can prove the following vector identity.
Suppose u = hu1 , u2 i, v = hv1 , v2 i, and w = hw1 , w2 i. Then
u · (v + w) = u · v + u · w.
(P4) Following the same line of thinking and using the Scalar Multiplication Theorem,
you can prove the following vector identity.
Suppose u = hu1 , u2 i, v = hv1 , v2 i, and k is a scalar. Then
k(u · v) = (ku) · v = u · (kv).
(P5) If u = hu1 , u2 i, then
[u · u = kuk2 .
Proof.
u · u = u1 u1 + u2 u2 , by definition.
= u21 + u22
2
q
2
2
u1 + u2
=
= kuk2 .
16.4.2
Angle Between Two Non-Zero Vectors
Consider two non-zero vectors u and v. Move the two vectors so that the initial point of
both vectors coincide. Let the initial point of the two vectors be O, the terminal point of
u be A, and the terminal point of v be B.
276
CHAPTER 16. AN INTRODUCTION TO VECTORS
B
v
A
θ
u
O
−→
−−→
There are two angles with the initial side OA and the terminal side OB with measure in
[0, 2π]. The smaller angle θ of the two is called the angle between u and v.
If θ is the angle between two non-zero vectors u and v, then by definition,
0 ≤ θ ≤ π.
When u and v have the same direction, then θ = 0, and when u and v have the opposite
direction, then θ = π.
We say two non-zero vectors u and v are orthogonal if the angle θ between them is a right
angle.
The Dot Product Theorem. Let u and v be two non-zero vectors so that the angle
between them is θ. Then
u · v = kukkvk cos θ.
Proof. Move the two vectors so that the initial points of both vectors coincide. Let the
initial point of the two vectors be O, the terminal point of u be A, and the terminal point
−→
of v be B. Let AB be w. Then by the definition of the vector addition, w = v − u.
16.4. DOT PRODUCT BETWEEN TWO VECTORS
277
B
v
v−u
A
θ
u
O
By the Law of Cosines Theorem,
kv − uk2 = kuk2 + kvk2 − 2kukkvk cos θ.
The left side of the above equation = kv − uk2
= (v − u) · (v − u), by P5.
= (v + (−u)) · (v + (−u))
= (v + (−u)) · v + (v + (−u)) · (−u), by P3.
= v · (v + (−u)) + (−u) · (v + (−u)), by P2.
= v · v + v · (−u) + (−u) · v + (−u) · (−u), by P3.
= v · v − v · u − u · v + u · u, by P4.
= v · v − 2u · v + u · u, by P2.
= kvk2 − 2u · v + kuk2 , by P5.
Therefore,
kvk2 − 2u · v + kuk2 = kuk2 + kvk2 − 2kukkvk cos θ.
Collecting like terms,
−2u · v = −2kukkvk cos θ.
Multiplying both sides by − 12 , we get:
u · v = kukkvk cos θ.
Exercise. Find the angle between u = h3, 4i and v = h1, 7i. Round your answer to the
nearest degree.
278
CHAPTER 16. AN INTRODUCTION TO VECTORS
Answer. Let θ be the angle between u and v.
u · v = (3)(1) + (4)(7) = 31.
√
kuk = 32 + 42 = 5.
and
kvk =
√
12 + 72 =
√
√
50 = 5 2.
Therefore, by the Dot Product Theorem,
√
31 = (5)(5 2) cos θ.
That is,
cos θ =
31
√ .
25 2
and
θ = cos−1
31
√
25 2
≈ 29◦ .
Since u · v is a scalar, (see P1), the Trichotomy Law holds.
Corollary to the Dot Product Theorem. Let u and v be two non-zero vectors so
that the angle between them is θ. Then
1. u · v = 0 if and only if u and u are orthogonal.
2. u · v > 0 if and only if θ is acute.
3. u · v < 0 if and only if θ is obtuse.
Proof of (1). Suppose u · v = 0.
Then by the Dot Product Theorem, 0 = kukkvk cos θ. Since u and v are two non-zero
vectors, kuk =
6 0 and kvk =
6 0. Therefore, cos θ = 0. The general solution of this equation
is θ = 2nπ ± cos−1 (0), for any integer n. By definition, θ lies in the interval [0, π]. The
only particular solution of cos θ = 0 in the interval [0, π] is cos−1 (0). That is, θ = π2 .
Now suppose u and u are orthogonal.
Then cos θ = 0. By the Dot Product Theorem, u · v = 0.
16.4. DOT PRODUCT BETWEEN TWO VECTORS
279
Proof of (2). Suppose u · v > 0.
Then by the Dot Product Theorem, 0 < kukkvk cos θ. Since u and v are two non-zero
vectors, kuk > 0 and kvk > 0. Therefore, cos θ > 0. By definition, θ lies in the interval
[0, π]. Since cos θ > 0, θ lies in the first quadrant. Therefore, θ is acute.
Now suppose θ is acute.
Then cos θ > 0. Since u and v be two non-zero vectors, kuk > 0 and kvk > 0. Therefore,
kukkvk cos θ > 0. By the Dot Product Theorem, u · v > 0.
The proof of (3) is left as an exercise.
Exercise. Prove part (3) of the Corollary to the Dot Product Theorem.
16.4.3
Projection of a Vector Along Another Vector
We have seen that any non-zero vector u = hu1 , u2 i can be written as a sum of two
orthogonal vectors; namely u1 i and u2 j. The vector u1 i is called the projection of u in
the direction of i. The vector u2 j is called the projection of u orthogonal to i.
Can we write a given non-zero vector u = hu1 , u2 i as a sum of two orthogonal vectors so
that one of the orthogonal vectors is along a given vector a? The answer is yes.
Suppose u and a are non-zero vectors and they have a common initial point. Suppose the
angle between them is θ. We will denote the vector the projection of u in the direction of
a as proja u.
The angle θ can be acute, obtuse, right, or zero.
If θ = 0, then clearly the proja u = u and the vector the projection of u orthogonal to a is
0. If θ is right, then the proja u = 0 and the vector the projection of u orthogonal to a is
u.
Now let us consider the other two cases.
u
u
θ
a
θ
a
280
CHAPTER 16. AN INTRODUCTION TO VECTORS
In the following figure, the “blue” vector is the vector proja u, and the “red” vector is the
projection of u orthogonal to a.
u
u
θ
a
θ
a
proja u
proja u
When θ is acute, the norm of proja u is kukcosθ and the direction of proja u is
1
a.
kak
1
When θ is obtuse, the norm of proja u is −kukcosθ and the direction of proja u is − kak
a.
Therefore, in either case,
proja u = kukcosθ
1
a.
kak
If we scalar multiply the right side of above equation by
proja u = kukkakcosθ
1
a.
kak2
Now by the Dot Product Theorem,
proja u =
u·a
a.
kak2
By the definition of vector addition,
the projection of u orthogonal to a = u − proja u.
Notice that we can write proja u as:
u·a
1
proja u =
a.
kak kak
kak
,
kak
then
16.4. DOT PRODUCT BETWEEN TWO VECTORS
281
Therefore,
u · a
.
kproja uk = kak Since kak > 0, the above is the same as
kproja uk =
|u · a|
kak.
Example. Suppose u = h3, 4i and v = h1, 7i. Find projv u and kprojv uk.
Answer.
u · v = (3)(1) + (4)(7) = 31.
√
√
kvk = 12 + 72 = 50.
Therefore,
projv u =
31
h1, 7i.
50
and
kprojv uk =
16.4.4
√31 .
50
Work Done by a Constant Force moving an Object
along a Straight Line
Consider a little boy pulling a cart along the x-axis in the direction of i with a constant
force F (in force units).
F
i
Suppose the cart moves along the x-axis a distance of d (in distance units). The vector
d = di is called the displacement vector. The component of F that contributes to the
motion of the cart is proji F . The work done by the boy (by the constant force F ) moving
the card a distance d is defined as:
The work done by a constant force F moving an object a distance d = proji F d.
That is,
work done =
F ·i
kik
d
= (F · i)d, because i is a unit vector.
= F · (di), by P4.
=F ·d
Work Done by a Constant Force Theorem. Suppose an object moves along a
straight line by the influence of a constant force F . Suppose d is the displacement
vector. Then the work done by F moving the object a distance d is F · d.
By M. Sunil R. Koswatta. First draft initiated: August 1, 2014.
First draft completed: December 31, 2014
282
Index
ab-ba theorem, 146
absolute value, 11, 17, 18, 18, 21
additive identity property, 24
additive inverse property, 24
adjacent side, 174
amplitude, 120
angle, 97
angle between vectors, 276
angle sum of a triangle, 105, 107, 109,
110, 172, 176, 182
Archimedean property, 74
arithmetic sequence, 65
ASA theorem, 179, 181, 194, 272
asymptote, 139, 140, 143
complex number multiplication theorem,
256
complex plane, 251
concavity, 29
constant angular speed, 235
constant speed, 235
continuity, 29
converse of the Pythagorean theorem,
172
corollary, 56
corollary to the dot product theorem,
278
critical points, 26, 27
cross multiplication, 180–185
cross multiplication algorithm, 179, 185,
186, 195, 206
behavior near each zero, 40, 40, 57
binomial square identities, 8, 11, 198
decreasing, 29
DeMoivre’s theorem, 257
difference of squares, 8, 10, 12, 22, 26,
198, 221, 229
direction, 264, 264
discriminant, 24, 25, 27, 92, 223
displacement vector, 282
distributive property, 13, 24, 87, 221,
253
division by zero, 14, 58
calculus, 17, 36, 58, 212
circular motion, 235
common difference, 65
completing the square, 7, 16, 17, 21, 22,
24, 35, 159, 248
complex conjugate, 254
complex equation, 260
complex nth roots theorem, 260
complex number, 253
complex number division theorem, 256
283
dot product, 274
dot product theorem, 276, 278, 280
double-angle identities, 213
irreducible, 26, 27, 36, 40, 52, 92
isosceles triangle theorem, 105
larger angle of a triangle theorem, 178
law of cosines, 187, 189, 190, 195, 197,
277
law of sines, 180, 182–186, 195
lemma, 135
lemma one, 135
lemma two, 135
limit of a function, 17
long division, 55, 56, 58
longer side of a triangle theorem, 178
end behavior, 29, 30, 31, 33, 35, 38, 40,
42, 44–49, 52, 58
equilateral triangle theorem, 105
Euclidean Algorithm, 56
Euclidean algorithm, 55
finite geometric series, 71
finite series, 63
four properties theorem, 9, 9–15, 81
general solution to the cosine equation,
164
general solution to the sine equation,
161
general solution to the tangent equation,
168
general term, 62
geometric sequence, 70
mathematical induction, 76, 77, 79, 257
matrix form, 85, 89, 90, 93
maximum, 31, 120, 127, 128
minimum, 30, 32, 33, 120, 127, 128
multiplicative identity property, 13
multiplicative inverse property, 13
non-vertical asymptote, 56, 57, 58
norm, 264, 265–268, 280
nth partial sum, 63
Heron’s formula, 196
hole, 57, 57, 58
horizontal asymptote, 57
one dimensional distance formula, 18
one-to-one, 145, 148, 150, 153
opposite direction, 264, 265, 276
opposite side, 174
identity, 8, 199
imaginary axis, 251
imaginary numbers, 251
imaginary part, 253
imaginary unit, 251
increasing, 29
inductive step, 76
Infinite Geometric Series, 75
infinite series, 75
initial point, 263
integer powers theorem, 69
parallelogram theorem, 266
partial fraction decomposition, 87
period, 119
perpendicular bisector theorem, 105
PFD with irreducible quadratic factors
theorem, 92
PFD with linear factors theorem, 88
phase shift, 124, 125
284
polar coordinates, 243
polar equation, 243
product-to-sum identities, 219
projection, 279, 280
proof by contradiction, 75
Pythagorean theorem, 106, 108–110,
112, 172, 177, 178, 187–189, 197
sum-to-product identities, 220
super-star identities, 207, 210, 221–224
symmetric, 135, 158
tangent to a circle theorem, 130
terminal point, 263
theorem five, 74
theorem four, 20, 21
theorem one, 11, 11, 16
theorem six, 75
theorem three, 20, 21, 25, 26, 74
theorem two, 15, 15, 17
three identities theorem, 8, 80
triangle inequality, 178, 198
triangle with standard notations, 171
trichotomy law, 7, 7, 24, 26, 257, 271,
272, 278
trigonometric numbers of 0, 106
trigonometric numbers of a triangle, 174
trigonometric numbers of pi/2, 111
trigonometric numbers of pi/3, 109
trigonometric numbers of pi/4, 108
trigonometric numbers of pi/6, 107
two dimensional distance formula, 112
quadratic formula, 21, 23, 27, 35, 159,
223
real part, 253
reflection theorem, 147
restricted cosine function, 150
restricted sine function, 148
restricted tangent function, 152
same direction, 264, 264, 266, 271, 276
SAS Theorem, 105
SAS theorem, 179, 189, 194
scalar, 263
scalar multiplication, 268
scalar multiplication theorem, 272
series, 63
similar, 30, 31, 32, 34, 43–45, 101, 104,
273
slant asymptote, 58
slope of a line theorem, 130
slopes of perpendicular lines theorem,
204
solving a triangle, 171
square-root principle theorem, 10, 206,
215
squares are nonnegative theorem, 8, 25
SSS theorem, 179, 190, 195
standard polar form, 255
standard position, 98
unique, 55, 88, 92, 101, 104, 105, 117,
130, 133, 138, 140, 142, 145, 146,
240, 248, 249, 251, 255, 268
unit vector, 267, 269, 282
vector, 263
vector addition theorem, 271
vertex, 29, 30–33, 35, 97, 97, 98, 171,
240, 241
vertical asymptote, 43, 44–50, 52, 53,
134
work, 282
285
zero, 29, 30, 32, 33, 35, 38, 40, 42, 44,
46–48, 52
zero product property theorem, 7, 10,
13, 22, 228, 229
zero vector, 264
286