Download Document

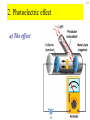
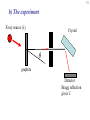
1
Chapter 29
Particles and Waves
2
There is nothing new to be discovered
in physics now. All that remains is
more and more precise measurement.
-- William Thomson, Lord Kelvin
(Address at the British Association for the Advancement
of Science, 1900).
Quantum Physics
• 2nd revolution in physics:
– Starts with Planck ~1900
– Contributions from Einstein, Bohr, Heisenberg,
Schrödinger, Born, Dirac, de Broglie …. over 25 years
• Cornerstones:
– Wave-particle duality
– Uncertainty principle
• Correspondence
– Applies for small dimensions
• Planck’s constant: h = 6.6 x 10-34Js
• As h -> 0, quantum physics -> classical
3
Solvay conference, 1927
4
Front row: I. Langmuir, M. Planck, M. Curie, H. A. Lorentz, A. Einstein, P. Langevin, C. E.
Guye, C. T. R. Wilson, O. W. Richardson. Second row: P. Debye, M. Knudsen, W. L. Bragg, H. A.
Kramers, P. A. M. Dirac, A. H. Compton, L. V. de Broglie, M. Born, N. Bohr. Standing: A.
Piccard, E. Henriot, P. Ehrenfest, E. Herzen, T. De Donder, E. Schroedinger, E. Verschaffelt, W.
Pauli, W. Heisenberg, R. H. Fowler, L. Brillouin.
5
Solvay conference, 1927
Pauli
Bragg
Planck
Curie
Born
Bohr
Dirac
Lorentz
Einstein
Front row: I. Langmuir, M. Planck, M. Curie, H. A. Lorentz, A. Einstein, P. Langevin, C. E.
Guye, C. T. R. Wilson, O. W. Richardson. Second row: P. Debye, M. Knudsen, W. L. Bragg, H. A.
Kramers, P. A. M. Dirac, A. H. Compton, L. V. de Broglie, M. Born, N. Bohr. Standing: A.
Piccard, E. Henriot, P. Ehrenfest, E. Herzen, T. De Donder, E. Schroedinger, E. Verschaffelt, W.
Pauli, W. Heisenberg, R. H. Fowler, L. Brillouin.
6
Part I: Particle nature of light
7
1. Blackbody radiation
a) Blackbody
• All objects radiate and absorb electromagnetic
radiation
• At equilibrium, rate of absorption = rate of emission
• Best absorber is best emitter
– Perfect absorber is perfect emitter
Cavity is model of a
perfect blackbody
8
b) Emmitance spectrum: the problem
Plot of intensity vs wavelength
– Depends only on temperature
Experimental spectrum:
9
Theory
Classical prediction:
The UV catastrophe
Based on idea that all
oscillations equally
probable, more oscillations
at lower wavelength
Violates common sense and
experiment
10
c) Energy quantization: the solution
Absorption and emission occur in discrete quanta only
Energy of quanta proportional to frequency
E  nhf ; n  0,1,2,3...
For small wavelength (high freq), quanta are large. If kT <
quantum, radiation not possible.


11
d) Planck’s constant, h
E  nhf  hc /;
n  0,1,2,3...
• Planck found a “fudge factor” by “happy guesswork” to make
the experiment fit. He developed a quantization theory to
predict the value h.
– “lucky artifact of more fundamental reality yet to be discovered”
h  6.626  10 34 Js
• Nobel prize, 1918

12
2. Photoelectric effect
a) The effect
13
b) Expectations and observations
Experiment
Expectation
Observation
Increase intensity
- Max energy increase - Max energy constant
- Current increase
- Current increase
- Time lag decrease
- No time lag
Increase
Frequency
- Max energy constant
- No threshold
14
Observed frequency dependence
15
b) Expectations and observations
Experiment
Expectation
Observation
Increase intensity
- Max energy increase - Max energy constant
- Current increase
- Current increase
- Time lag decrease
- No time lag
Increase
Frequency
- Max energy constant - Max energy prop to freq
- Threshold frequency
- No threshold
characteristic of metal
16
c) Einstein theory
KEmax = hf - W0
Energy of photon
(from Planck)
Work required to
remove electron
17
• Found same value for h as Planck had
• Nobel prize in 1921
• In 1913, Planck recommended Einstein for
membership in the Prussian Academy.
“Notwithstanding his genius, he may sometimes have
missed the target in his speculations, as, for example, in his
hypothesis of light quanta.”
18
3. The Compton Effect, 1923
a) The effect: Scattering of x-ray by
electron changes the wavelength
19
b) The experiment
X-ray source ()
Crystal
q
graphite
Detector
Bragg reflection
gives ’
20
c) Classical prediction
- incident wave excites electron at frequency f
- electron radiates at frequency f
21
d) Compton’s explanation
- Conservation of energy:
hf  hf  KE
- Conservation of Momentum: p  ppe
- Energy-momentum relation for light:

E hf h
p 

c
c 
Combining these equations
 gives:
h
  
(1 cos )
mc

Nobel prize, 1928
Definitive evidence for photons

’
22
Part II: The wave nature of particles
23
4. The de Broglie wavelength, 1924
a) The hypothesis
The dual nature observed in light is present in matter:
A photon has energy
E  hf  hc / 
From electromagnetism,
E  pc
}
h

p
By analogy, de Broglie
 proposed that a particle with
momentum p is associated with a wave with wavelength:


h

p
24
b) Electron diffraction/interference
QuickTime™ and a
TIFF (U ncompressed) decompressor
are needed to see this picture.
QuickTime™ and a
TIFF (U ncompressed) decompressor
are needed to see thi s picture.
25
b) Interpretation of the particle wave
Waves and particles propogate and interfere like
waves, but interact like particles.
The intensity of the wave (represented by a wave
function at a point in space represents the
probability of observing a particle at that location.
26
5. The Heisenberg Uncertainty Principle
The wave nature of particles means that position and momentum
(wavelength) cannot simultaneously be determined to arbitrary
accuracy. The smaller the slit above, the better the y-position is
known, but the greater the spread in y-momentum.
27
The principle applies separately to any
component of momentum and position:
h
py y 
4
h
px x 
4

and to energy and time:

h
Et 
4