Download 22 Mar 2015 - U3A Site Builder

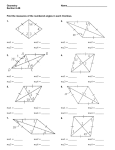
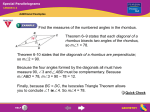
STEYNING & DISTRICT U3A
Discovering Mathematics
Session 22
Mathematical Problems
&
Bayes Theorem
Area of a Rhombus
A rhombus, ABCD, has sides of length 10. A circle with centre A passes through C
and a circle with centre B passes through D. The circles are tangential to each
other. What is the area of the rhombus?
The diagonals of a rhombus bisect each other
and meet at right angles.
R is the radius of larger circle, and r the
radius of the smaller.
The area of a triangle = base*height/2.
Considering the four right triangles, the area of
rhombus ABCD = 4 * (R/2) * (r/2) / 2 = Rr/2.
Applying Pythagoras to one of the right
triangles, (R/2)2 + (r/2)2 = 102, from which
R2 + r2 = 400.
Since the circles meet at a tangent, on AB, we
have R − r = 10.
Thus (R − r)2 = R2 − 2Rr+ r2 = 100, and so 2Rr = 300.
and the area of the rhombus = Rr/2 = 75 square units.
New Mereology
(From Prof. Ian Stewart’s ‘Cabinet of Mathematical Curiosities)
An American inventor Lee Sallows coined this term to describe a mathematical
curiosity which allocates whole numbers to letters, such that the name of a number
is described numerically. eg O+N+E = 1, T+W+O = 2 & T+H+R+E+E = 3.
He also suggested that the value for each letter should be unique.
The first example; ONE = 1 demonstrates that some of the letters must have
negative values. Ie if E=1 & N=2, then O=-2.
By substituting these values in TWO, NINE & TEN we deduce the values; I=4, T=7
& W=-3.
To make THREE ‘perfect’ we must assign new values to H & R. If H=3 then R=-9.
Ie 7+3+R+1+1 = 3
The equation for EIGHT gives 1+4+G+3+7 = 8, or G=-7.
FOUR needs 2 new letters to be assigned. If F = 5, then U =10.
Then for FIVE, 5+4+V+1 = 5 & V = -5, giving SEVEN as S+1-5+1+2 = 7 & S=8
Now SIX produces 8+4+X = 6 and X=-6.
L is the only unknown in ELEVEN & TWELVE, ie 1+L+1-5+1+2 = 11, giving L= 11
And this value of L also produces a ‘perfect’ result for TWELVE.
Thus with the selected values, we have perfect results for all numbers from 1 to 12.
New Mereology (Cont.)
However, if we use these values for the number THIRTEEN, we come unstuck
Ie, 7+3+4-9+7+1+1+2 = 16 NOT 13.
Apparently, any other assignment of numbers to letters will result in failure to find the
‘perfect’ relationship for THIRTEEN.
Further, For ZERO, we get Z+1-9-2 = 0, giving Z=10, but this is the value already
assigned to U, so this is not ‘perfect’ either
Lee Sallows has established that there are alternative assignments of numbers to
letters which will produce ‘perfect’ relationships for ZERO to TWELVE, but not
beyond.
Bayes’ Theorem
•
•
•
•
•
•
Today, the Discovering Mathematics Group discovered the prevalence
of the 200 year-old Bayes Theorem in much of modern life ... none of
us had heard of this before .... but it explains a lot of what goes on
around us, in such diverse areas as medicine, loyalty cards, the
courts, spam filters, search engines and much more ... even the
human brain has Bayesian inferencing characteristics.
In case your wondering, the theorem was developed by the nonconformist Rev Bayes FRS in the 18th century while studying theology
and logic at Edinburgh University.
searching YOUTUBE for Bayes Theorem you will come across many
interesting tutorials on the subject; here are just three that we used
today to inform ourselves:
www.youtube.com/watch?v=2Df1sDAyRvQ (Preview)
www.youtube.com/watch?v=za7RqnT7CM0
www.youtube.com/watch?v=j2tNxIaGpR4
That’s it Folks!