Download Persistence and flow reliability in simple food webs

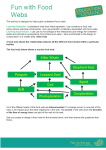
Ecological Modelling 161 (2003) 117 /124
www.elsevier.com/locate/ecolmodel
Persistence and flow reliability in simple food webs
Ferenc Jordán a,b,c,*, István Scheuring c, István Molnár a
a
Evolutionary Genetics Research Group, Department of Genetics, Eötvös University, Budapest, H-1117, Pázmány P.s. 1/c, Hungary
b
Collegium Budapest (Institute for Advanced Study), Budapest, H-1014, Szentháromság u. 2., Hungary
c
Eötvös University, Department of Plant Taxonomy, Research Group of Ecology and Theoretical Biology, Budapest, H-1117, Pázmány
P. s. 1/c, Hungary
Received 4 January 2002; received in revised form 31 May 2002; accepted 26 August 2002
Abstract
Twenty-five model food webs can be designed from five points (species) and five links (trophic interactions), if they
contain a single top-predator (i.e. sink webs). According to a simple topological approach, we presented elsewhere a
reliability theoretical analysis of this set of food web graphs. The question addressed here is how network flow
reliability is related to the dynamical behavior and stability of these ‘model communities’. We simulated the behavior of
these webs and calculated their persistence, according to four models: (1) with symmetrical interaction coefficients
between species; (2) with asymmetrical interaction coefficients and lower death rates for predators; and (3) with
absolutely and (4) relatively perturbed, formerly persistent parameter sets of the asymmetrical model. We used both
Lotka /Volterra (LV) and Holling II-type equations (with switching effect). Thus, we had eight persistence values for
each web. Persistence (a dynamical property) and flow reliability (a structural property) were analyzed. We found that
(1) reliable flow pattern is associated with high persistence in the Holling models, while the LV models predict no
consistent correlations; (2) in asymmetrical situations, persistence is always much higher (in both LV and Holling
models); and (3) the predictions of Holling models (versus LV models) are much less sensitive to local perturbations.
Based on these results, we conclude that (1) reliable network flows can contribute to persistence only if switching is
possible; (2) asymmetrical interactions increase persistence, independently of the switching effect but it indicates
persistence in Holling II model; (3) switching makes the relationship much more predictable between structure and
dynamics. Thus, the network design is less useful predictor of persistence without switching effect but well can ensure
dynamical stability under the conditions of the Holling II model. We have presented how various dynamical models
predict different behavior of modelled communities characterized by the same structure and complexity. Complementing dynamical with structural analysis may further increase our understanding of persistence in food webs.
# 2002 Elsevier Science B.V. All rights reserved.
Keywords: Food web; Interaction symmetry; Network design; Persistence; Reliable flows; Switching effect
1. Introduction
* Corresponding author. Tel.: /36-1-381-21-87; fax: /36-1381-21-88
E-mail address: [email protected] (F. Jordán).
It was analyzed elsewhere how food web structure affects the reliability of nutrient flows in
simple, model sink webs containing five points
0304-3800/02/$ - see front matter # 2002 Elsevier Science B.V. All rights reserved.
PII: S 0 3 0 4 - 3 8 0 0 ( 0 2 ) 0 0 2 9 6 - X
118
F. Jordán et al. / Ecological Modelling 161 (2003) 117 /124
and five links (Jordán and Molnár, 1999). However, the relationship between flow reliability and
some characteristics of dynamical stability remained unclear. Here, we attempt to study how a
particular type of dynamical stability (persistence)
is related to reliability, a topological property.
The reliability of energy flows in trophic flow
networks can be increased by simply creating new
links: enhanced complexity (i.e. connectance) provides new transport pathways of food and energy
(cf. MacArthur, 1955). But dynamical stability
may decrease with increasing complexity (Gardner
and Ashby, 1970; May, 1973; Pimm, 1984). Thus,
it is worth studying how dynamical behavior
relates to reliability in equally complex food webs
(containing the same number of points and links,
i.e. characterized by the same connectance). Doing
so, we can escape the traditional debates concerning the relationship between complexity and stability (e.g. De Angelis, 1975; McNaughton, 1977;
see also Siljak, 1975; and for a recent contribution:
McCann et al., 1998).
Our main question is how persistence relates to
reliability, a structural network property (defined
below). Here, a web is considered persistent if the
densities of all five species remain above a given
threshold after an ‘ecologically reasonable’ time.
This measure of persistence is general and may be
more adequate stability property (McCann et al.,
1998), than the widely used local asymptotic
stability of fixed points (e.g. May, 1973). Various
persistence values are calculated and plotted
against flow reliability. Results are discussed in
the context of connecting pattern to process in
ecology (cf. Winemiller and Polis, 1996).
2. Methods
First we used simple Lotka /Volterra (LV)
equations for calculating persistence. Population
dynamics is described by the following set of
equations:
n
X
dxi
ri aij xj xi ; i 1; . . . n:
(1)
dt
j1
Here, xi is the population density of species i, ri
is the per capita reproduction (ri /0) or decay
(ri B/0) rate. The parameter aij indicates the per
capita effect of species j on the per capita growth
rate on species i. If species i is a producer then
aii B/0, otherwise let aii /0 (Pimm, 1982). Of
course, if there is no predatory interaction between
species i and j, then aij /aji /0. Two LV models
were derived, as follows.
2.1. The basic models
2.1.1. Symmetrical LV model
Here, ri is an evenly distributed random variable
over the interval (0 1) if species i is a basal species,
while ri is selected randomly from (/1 0) if species
i is intermediate or top species. Similarly, aij is
over the interval (0 1) if i is the predator of j, and
aji is selected from (/1 0) if i eats j (or if i /j for
producers, see May, 1973; Pimm, 1982). This basic
model can be used to describe situations where we
have little information about species and species
interactions.
2.1.2. Asymmetrical LV model
The parameter ri is defined as in the symmetrical
LV model, and aij is in (0 1) for the predator i .
However, aji //aij /(10/5j ), where j is a random variable in (/1 1). This asymmetry in interaction parameters comes from the observation
that the size of a predator is in most cases larger
than the size of its prey (Warren and Lawton,
1987; Cohen et al., 1993; now we do not consider
the problems of parasites in food web theory, see
Marcogliese and Cone, 1997) and only a fraction
of energy directs to reproduction. The ½aij /aji ½ ratio
may differ widely between trophic interactions, but
it is generally around 1/100 for vertebrate/invertebrate, and 1/10 for vertebrate/vertebrate interactions (Pimm, 1982; Jonsson and Ebenman, 1998).
Also, as a consequence of larger body size,
predator death rates are lower. We choose ri
over the interval (/1/15 0) for the predators.
Thus, the asymmetrical model holds for situations
where the consumers are characteristically larger
than the consumed species.
F. Jordán et al. / Ecological Modelling 161 (2003) 117 /124
119
2.2. Simulations
2.4. Switching effect
Eq. (1) was numerically integrated by the
second-order predictor-corrector method for each
web (according to each model) after selecting 2000
sets of random parameters (ri and aij ). Initial
densities (xi (0)) were selected randomly from the
interval (0 1) for each parameter set. After the
initial transients was discarded, the persistence
index was measured as the ratio of parameter
sets allowing the density of all the five species to
remain over a critical threshold (d /1015) after t
(t/200) steps. Here, we are interested in whether
each population of the ecosystem can survive (at
this ‘ecological’ time-scale). The sensitivity of
persistence to various t (t /100, 200, 500) and d
(d/1010, 10 15 and 10 20) parameters was
studied: not surprisingly, extinction was more
frequent if either t (longer simulation run) or d
(high threshold density) was higher, but the results
remained qualitatively similar. Each model presented below were simulated with the parameters
t/200 and d/1015.
In order to analyze whether switching of predators affects the relationship between reliability
and persistence, we have studied models describing
situations according to the Holling II-type functional response (Holling, 1959; Chesson, 1983).
The main advantage of the LV model is its
structural simplicity and the low number of
parameters needed to describe it. However, as a
Taylor expansion of a general dynamical model, it
can be a good approximation of real dynamics
only in the neighborhood of some equilibrium. As
a more sophisticated model, the Holling II-type
function takes into account the possibility of
switching (we now consider only positive switching, Abrams, 1987), as well as the searching and
handling times of predation. Here, the LV model
modifies to:
2.3. Sensitivity to perturbation
We analyzed two further stability indices, in
order to study how local perturbations of formerly
persistent parameter sets of the LV model affect
dynamical behavior.
2.3.1. Absolute perturbation
Here, 1000 random parameter sets that yield
persistent webs were chosen and parameters were
perturbed 10 times according to the rule ri? /ri /
j , aij? /aij /j, where j is a random variable in (/
0.1 0.1). (To change the sign of ri or aij by
perturbation was not allowed, of course.) By this
method, we tested how persistence is maintained if
parameters change within given limits.
2.3.2. Relative perturbation
It is similar to the previous case but ri and aij
were modified to ri (1/j ) and aij (1/j ) after
perturbation.
n
X
dxi
ri hij (x)aij xj xi bii x2i ;
¯
dt
j1;
(2)
j"i
where
v
Xij
hij (x)
¯
gj vik xk
(3)
k Li
if species i is the predator of species j, or
vji
X
hij (x)
¯
gi vki xk
(4)
k Li
if species i is the prey of predator j. The parameter
gj is the half-saturation density of the prey j , vij is
a constant between zero and one indicating the
preference of species i for consuming species j ,
thus Sk Li vik /1, where Li denotes the indexes
of all alternative preys of predator i. If species i is
a primary producer (ri /0) then bii B/0 to set a
finite carrying capacity. For species being in the
higher trophic level bii /0. The variables ri , aij are
selected symmetrically and asymmetrically as in
the LV model previously, while the new parameters gj and vij are chosen randomly from the
(0 1) interval in every case.
120
F. Jordán et al. / Ecological Modelling 161 (2003) 117 /124
2.5. The reliability of network flows
The above defined persistence measures were
compared to flow reliability, the probability that
the sink point remains connected to at least one
source, despite probabilistic deletions of points
(see also Barlow and Proschan, 1965; Aggarwal,
1993), with fixed and equal probability for all four
points except the sink (Jordán and Molnár, 1999),
according to the equation:
4 X
4 i (4i)
R 1
Fi ;
(5)
pq
i
i1
where the p deletion probability equals 0.01 (and
‘survival’, q /1/p /0.99), 4 indicates the number
of points possibly deleted (all except the sink), and
Fi is the ‘fatal ratio’. This is defined as the ratio of
point sets containing i points which results in
disconnection between the sink and the sources,
when deleted (i/1,. . .,4). For example, consider
web #15 in Fig. 1: two points out of four can be
deleted in six combinations (with joint links, of
course). In four out of six combinations, the sink
species become disconnected to producers. Thus,
F2 for web #15 is 4/6. Evidently, F4 /1 for each
web. Based on their R -values, these 25 webs can be
ranked in four reliability classes, as shown at Fig. 1
(the difference in R between two webs belonging
to different reliability classes is at least two orders
of magnitude larger, than that between two webs
belonging to the same class). The structure of food
webs clearly influences flow reliability (for an early
idea of similar nature, see MacArthur, 1955).
3. Results
The persistence values of the 25 webs (i.e. the
ratio of persistent webs), according to the above
simulations, are plotted against reliability (averaged for R -classes, Fig. 2; open boxes and dashed
lines correspond to LV, while asterisks and solid
lines correspond to Holling II-type simulation
results).
Under the conditions of the symmetrical LV
model (Fig. 2a), flow reliability correlates positively with dynamical stability. According to the
symmetrical Holling model, there is no significant
correlation between persistence and reliability.
(Note that the Holling simulations generally give
lower persistence: this is an artefact, depending
only on model parameters g and v. These were
selected from (0 1), since we have no assumptions
on their symmetry.) Fig. 2b shows how the
asymmetry in interaction parameters and higher
death rates of predators increase persistence. The
correlation between persistence and reliability is
positive according to the Holling model but
negative in the LV case. If persistent parameter
sets are slightly perturbed, extinction may appear.
Holling models behave in a more or less similar
way (significant positive correlation) in the cases
of both relative (Fig. 2c) and absolute (Fig. 2d)
perturbations. However, these local perturbations
influence to a smaller extent, but qualitatively
differently the behavior of the LV systems (no
significant correlation in Fig. 2c, while negative
correlation in Fig. 2d).
4. Discussion
Persistence, as a type of stability (cf. Pimm,
1984) was calculated by LV and Holling II-type
equations for a well defined set of model food
webs. This set consists of all possible sink webs
designed from five points and five links. The flow
reliability of these webs was known (Jordán and
Molnár, 1999).
The average persistence values for the different
reliability classes show (Fig. 2) that more reliable
energy flows can be associated with either higher
(e.g. symmetrical LV and asymmetrical Holling
models) or lower (e.g. asymmetrical LV model)
persistence. In some models, there is no significant
correlation (relatively perturbed, asymmetrical LV
and symmetrical Holling model).
We found that asymmetry in interaction coefficients and lower death rates for predators lead to
much more persistent ‘model communities’ (Fig.
2b/d, and cf. Hughes and Roughgarden, 1998).
Switching effect makes predictable the reliabilitypersistence relationship only under asymmetrical
conditions (cf. Pelletier, 2000). Thus, analyzing
switching and interaction symmetry in combina-
F. Jordán et al. / Ecological Modelling 161 (2003) 117 /124
121
Fig. 1. All of the possible sink food webs with five species (nodes) and five trophic interactions (links) (N/5, L /5, connectance: C/
0.5), ranked according to four classes of reliability (calculated by (5); slightly modified after Jordán and Molnár, 1999). Trophic flows
from producers (down) reach the single sink species (always on the top) in the most reliable way in R1 class webs.
tion is more informative than studying switching
in itself (for the relationship between switching,
stability, and growth rates , see Matsuda et al.,
1986).
Various dynamical behaviors under different
model conditions appeared because the exact
mathematical conditions for the persistence are
determined by the complex algebraic combinations
of interaction parameters (Hallam, 1980). Thus,
even if food web complexity is similar, the
relationship between structure and dynamics can
be strikingly unpredictable. Mechanisms being
sensitive to the details of modelling include, for
example, the interactions between trophic levels
(Hairston et al., 1960; Fretwell, 1977; Oksanen et
al., 1981), or reticulate control pathways (Polis
and Strong, 1996).
Our results suggest that, if interaction coefficients are nearly symmetrical (consider insectparasitoid interactions), switching makes the relationship between structure and dynamics less
predictable (Fig. 2a). In this case, good network
design can be dynamically advantageous without
switching possibility, too. Note that the conditions
of the symmetrical model seem to apply much
more to specialist predators. However, if switching
is possible and accompanied by asymmetrical
interactions, reliable flow structure well predicts
persistence. These findings support that network
design principles have dynamical consequences on
122
F. Jordán et al. / Ecological Modelling 161 (2003) 117 /124
Fig. 2. The simulation results (i.e. persistence: the ratio of persistent webs) for model food webs were averaged for different reliability
classes (from R4, containing the least reliable webs, to R1, containing the most reliable ones). Open boxes and dashed lines mark the
results for the LV simulations, while asterisks and solid lines mark the results of the Holling simulations. Linear fit comes from the
Marquardt /Levenberg algorithm, weighted by standard deviation values. We also give the asymptotic standard error of the slope: a,
symmetrical interaction coefficients (LV: r/0.1329/0.0096, Holling: n.s.); b, asymmetrical interaction coefficients and lower death
rates for predators (LV: r //0.07079/0.0039, Holling: r/0.0279/0.0067); c, asymmetrical case with relative perturbation (LV: n.s.,
Holling: r/0.02389/0.011); d, asymmetrical case with absolute perturbation (LV: r//0.01439/0.01, Holling: r/0.0369/0.0086).
network dynamics and evolution. For example,
the fragility of marine wasp/waist systems can be
understood as a consequence of unreliable network architecture (Vasconcellos et al., 1997; Cury
et al., 2000). Further, even if our approach does
not take into account recycling pathways (Odum,
1969; Ulanowicz, 1986, 1988; Vasconcellos et al.,
1997), we still can investigate the effects of the
length and redundancy of pathways (web-like
versus chain-like architectures, Pahl-Wostl, 1997;
strictly corresponding to reliability classes) on
stability and performance (Büssenschütt and
Pahl-Wostl, 2000). Fig. 2 suggests that the sensi-
tivity of chain-like structures (R4 class of reliability) is higher under the Holling II conditions (cf.
Pahl-Wostl, 1997).
The most important tasks for future are: (1)
studying larger webs in order to detect possible
scale-dependence, (2) studying community webs
(i.e. not sink webs) in order to check whether the
‘sink web property’ causes any bias in results, and
(3) analyzing the dynamical behavior of each point
in each web in order to understand the relationship
between their exact network position and extinction risk (cf. the ‘functional niche’ concept, PahlWostl, 1997, and Jordán et al., 2002).
F. Jordán et al. / Ecological Modelling 161 (2003) 117 /124
Food web dynamics is a consequence of the
structure and interaction intensity, hence, if the
two need to be related, an analysis of dynamics
should be complemented with structural analyses
(cf. Silvert, 1983). The notorious question of how
to connect structure to dynamics can be answered
only by dual investigations (Winemiller and Polis,
1996; see also Jordán, 2000).
Acknowledgements
We thank Professor Gábor Vida and Viktor
Müller for useful comments on the manuscript.
F.J. is grateful to Professor Szathmáry and the
Collegium Budapest for excellent working conditions. Two anonymous Reviewers are also acknowledged for their helpful comments. The work
of F.J. is funded by the grants ‘OTKA F 029800’
and ‘OTKA F 035092’; I. Sch. is supported by the
grant ‘OTKA T 037726’. F.J. and I. Sch. hold the
Bolyai Research Grant of the Hungarian Academy
of Sciences.
References
Abrams, P., 1987. The functional responses of adaptive
consumers of two resources. Theor. Pop. Biol. 32, 262 /288.
Aggarwal, K.K., 1993. Reliability Engineering. Kluwer, Dordrecht.
Barlow, R.E., Proschan, F., 1965. Mathematical Theory of
Reliability. Wiley, New York.
Büssenschütt, M., Pahl-Wostl, C., 2000. A discrete, allometric
approach to the modeling of ecosystem dynamics. Ecol.
Model. 126, 33 /48.
Chesson, J., 1983. The estimation and analysis of preference
and its relationship to foraging models. Ecology 64, 1297 /
1304.
Cohen, J.E., Pimm, S.L., Yodzis, P., Saldaña, J., 1993. Body
sizes of animal predators and animal prey in food webs. J.
Anim. Ecol. 62, 67 /78.
Cury, P., Bakun, A., Crawford, R.J.M., Jarre, A., Quiñones,
R.A., Shannon, L.J., Verheye, H.M., 2000. Small pelagics in
upwelling systems: patterns of interaction and structural
changes in ‘wasp /waist’ ecosystems. J. Mar. Sci. 57, 603 /
618.
De Angelis, D.L., 1975. Stability and connectance in food web
models. Ecology 56, 238 /243.
Fretwell, S.D., 1977. The regulation of plant communities by
the food chains exploiting them. Persp. Biol. Med. 20, 169 /
185.
123
Gardner, M.R., Ashby, W.R., 1970. Connectance of large
dynamic (cybernetic) systems: critical values for stability.
Nature 228, 784.
Hairston, N.G., Smith, F.E., Slobodkin, L.B., 1960. Community structure, population control, and competition. Am.
Nat. 94, 421 /425.
Hallam, T.G., 1980. Community dynamics in a homogeneous environment. In: Hallam, T.G., Levin,
S.A. (Eds.), Mathematical Ecology. Springer, Germany,
pp. 242 /280.
Holling, C.S., 1959. Some characteristics of simple types of
predation and parasitism. Can. Entomol. 91, 385 /398.
Hughes, J.B., Roughgarden, J., 1998. Aggregate community
properties and the strength of species’ interactions. Proc.
Natl. Acad. Sci. USA 95, 6837 /6842.
Jordán, F., 2000. Is the role of trophic control larger in a
stressed ecosystem? Community Ecol. 1, 139 /146.
Jordán, F., Molnár, I., 1999. Reliable flows and preferred
patterns in food webs. Evol. Ecol. Res. 1, 591 /609.
Jordán, F., Scheuring, I., Vida, G., 2002. Species positions and
extinction dynamics in simple food webs. J. Theor. Biol.,
215, 441 /448.
Jonsson, T., Ebenman, B., 1998. Effects of predator /prey body
size ratios on the stability of food chains. J. Theor. Biol.
193, 407 /417.
MacArthur, R., 1955. Fluctuations of animal populations,
and a measure of community stability. Ecology 36, 533 /
536.
Marcogliese, D.J., Cone, D.K., 1997. Food webs: a plea for
parasites. TREE 12, 320 /325.
Matsuda, H., Kawasaki, K., Shigesada, N., Teramoto, E.,
Ricciardi, L.M., 1986. Switching effect on the stability of the
prey /predator system with three trophic levels. J. Theor.
Biol. 122, 251 /262.
May, R.M., 1973. Stability and Complexity in Model Ecosystems. Princeton University Press, Princeton, NJ.
McCann, K., Hastings, A., Huxel, G.R., 1998. Weak trophic
interactions and the balance of nature. Nature 395, 794 /
798.
McNaughton, S.J., 1977. Diversity and stability of ecological
communities: a comment on the role of empiricism in
ecology. Am. Nat. 111, 515 /525.
Odum, E.P., 1969. The strategy of ecosystem development.
Science 164, 262 /270.
Oksanen, L., Fretwell, S.D., Arruda, J., Niemelä, P., 1981.
Exploitation ecosystems in gradients of primary productivity. Am. Nat. 118, 240 /261.
Pahl-Wostl, C., 1997. Dynamic structure of a food web model:
comparison with a food chain model. Ecol. Model. 100,
103 /123.
Pelletier, J.D., 2000. Are large complex ecosystems more
unstable? A theoretical reassessment with predator switching. Math. Biosci. 163, 91 /96.
Pimm, S.L., 1982. Food Webs. Chapman and Hall, London.
Pimm, S.L., 1984. The complexity and stability of ecosystems.
Nature 307, 321 /326.
124
F. Jordán et al. / Ecological Modelling 161 (2003) 117 /124
Polis, G.A., Strong, D.R., 1996. Food web complexity and
community dynamics. Am. Nat. 147, 813 /846.
Siljak, D.D., 1975. When is a complex ecosystem stable? Math.
Biosci. 25, 25 /50.
Silvert, W., 1983. Is dynamical systems theory the best way to
understand ecosystem stability? In: Freedman, H.I., Strobeck, C. (Eds.), Population Biology. Springer, Germany,
pp. 366 /371.
Ulanowicz, R.E., 1986. Growth and Development: Ecosystems
Phenomenology. Springer, Berlin.
Ulanowicz, R.E., 1988. On the importance of higher-level
models in ecology. Ecol. Model. 43, 45 /56.
Vasconcellos, M., Mackinson, S., Sloman, K., Pauly, D., 1997.
The stability of trophic mass-balance models of marine
ecosystems: a comparative analysis. Ecol. Model. 100, 125 /
134.
Warren, P.H., Lawton, J.H., 1987. Invertebrate predator /prey
body size relationships: an explanation of upper triangular
food webs and patterns in food web structure? 74, 231 /235.
Winemiller, K.O., Polis, G.A., 1996. Food webs: what can they
tell us about the world? In: Polis, G.A., Winemiller, K.O.
(Eds.), Food Webs */Integration of Patterns and Dynamics.
Chapman and Hall, London, pp. 1 /22.