Download Print - Circulation Research

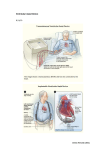
Evidence of Structural Remodeling in the Dyssynchronous
Failing Heart
Patrick A. Helm, Laurent Younes, Mirza F. Beg, Daniel B. Ennis, Christophe Leclercq, Owen P. Faris,
Elliot McVeigh, David Kass, Michael I. Miller, Raimond L. Winslow
Downloaded from http://circres.ahajournals.org/ by guest on June 18, 2017
Abstract—Ventricular remodeling of both geometry and fiber structure is a prominent feature of several cardiac
pathologies. Advances in MRI and analytical methods now make it possible to measure changes of cardiac geometry,
fiber, and sheet orientation at high spatial resolution. In this report, we use diffusion tensor imaging to measure the
geometry, fiber, and sheet architecture of eight normal and five dyssynchronous failing canine hearts, which were
explanted and fixed in an unloaded state. We apply novel computational methods to identify statistically significant
changes of cardiac anatomic structure in the failing and control heart populations. The results demonstrate significant
regional differences in geometric remodeling in the dyssynchronous failing heart versus control. Ventricular chamber
dilatation and reduction in wall thickness in septal and some posterior and anterior regions are observed. Primary fiber
orientation showed no significant change. However, this result coupled with the local wall thinning in the septum implies
an altered transmural fiber gradient. Further, we observe that orientation of laminar sheets become more vertical in the
early-activated septum, with no significant change of sheet orientation in the late-activated lateral wall. Measured
changes in both fiber gradient and sheet structure will affect both the heterogeneity of passive myocardial properties as
well as electrical activation of the ventricles. (Circ Res. 2006;98:0-0.)
Key Words: cardiac remodeling 䡲 computational anatomy 䡲 fiber architecture 䡲 dyssynchrony
D
importance to understanding DCM and such an understanding may lead to improved pacing therapies that will reverse
remodeling.12–14
Ventricular myocardium has a complex structural organization. Fiber orientation was first studied by means of fiber
dissections15–17 and histological measurements in transmural
plugs of ventricular tissue.18 –20 The principle conclusions of
this work were that cardiac fibers are arranged as counterwound helices encircling the ventricles and that fiber orientation is a function of transmural location, with fiber direction
being oriented predominantly in the base-apex direction on
the epicardial and endocardial surfaces and rotating to a
circumferential direction in the midwall. Subsequently, Le
Grice et al showed that collagen binds adjacent myocytes
together, forming layers known as lamina or sheets.21 Reorientation of sheets are responsible for substantial wall thickening during contraction.22 Nielsen et al developed histological methods for the systematic reconstruction of cardiac
ventricular geometry and primary fiber organization and
efficient computational methods for representing these anatomical data through the use of finite-element (FE) models.23
Development of these approaches has contributed significantly to our understanding of ventricular anatomy and its
ilated cardiomyopathy (DCM) is 1 of the most common
forms of heart muscle disease. In this disease, chronic
hemodynamic overload leads to increased wall stress. Subsequent adaptive responses of the heart include both ventricular
chamber dilation and myocyte hypertrophy to equalize wall
stress.1–3 Whereas such adaptations help to maintain pump
function over the short term, chronically, inadequate compensation leads to heart failure. Patients with DCM may also
exhibit intraventricular conduction delays, particularly of the
left bundle branch (LBB) type.4 – 6 The resulting asynchronous electrical activation produces dyssynchronous mechanical contraction and regional heterogeneity in wall stress.7–9
In particular, strain magnitude shows a marked phase delay
between early septal and late lateral shortening, with early
systolic stretch of the lateral wall occurring during septal
shortening.10 In patients with congenital heart block and
chronic right ventricular (RV) pacing, dyssynchronous contraction has been shown to result in significant structural
remodeling of left ventricular (LV) morphology as the early
activated septum thins and the later-activated lateral wall
hypertrophies.11 Understanding LV remodeling in the dyssynchronous failing heart, including alteration of ventricular
geometry as well as fiber architecture, is therefore of critical
Original received June 13, 2005; revision received October 14, 2005; accepted November 22, 2005.
From the Centers for Cardiovascular Bioinformatics & Modeling (P.A.H., R.L.W.) and Imaging Science (L.Y., M.I.M.) and Division of Cardiology
(C.L., D.K.), Johns Hopkins University, Baltimore, Md; Engineering Science (M.F.B.), Simon Fraser University, Burnaby, British Columbia, Canada;
and Laboratory of Cardiac Energetics (D.B.E., O.P.F., E.M.), National Heart Lung Blood Institute, National Institutes of Health, Bethesda, Md.
This manuscript was sent to Hiroyuki Suga, Consulting Editor, for review by expert referees, editorial decision, and final disposition.
Correspondence to Patrick Helm, 202 Clark Hall, Johns Hopkins University, 3400 N Charles St, Baltimore MD 21218. E-mail [email protected]
© 2005 American Heart Association, Inc.
Circulation Research is available at http://circres.ahajournals.org
DOI: 10.1161/01.RES.0000199396.30688.eb
1
2
Circulation Research
January 6/20, 2006
Downloaded from http://circres.ahajournals.org/ by guest on June 18, 2017
influence on both electrical and mechanical properties. However, histological reconstruction has limitations, taking weeks
to months to reconstruct a single heart and yielding a low
spatial resolution.
Diffusion tensor imaging24 (DTI) has emerged as a means
to overcome both these limitations by allowing noninvasive
characterization of cardiac tissue structure.25,26 In this technique, a tensor that represents the 3D diffusion of water in
each image voxel is estimated. The primary eigenvector of
this tensor points in the direction in which the rate of
diffusion is largest. Comparing DTI with histological measurements, it has been shown that the primary eigenvector of
the diffusion tensor is aligned with the cardiac fiber long
axis.25,26 In addition, in myocardial regions where diffusion is
anisotropic, we have recently shown that the tertiary eigenvector of the diffusion tensor is aligned with the surface
normal to the cardiac sheets.27 Finally, we have demonstrated
that DTI may be used to reconstruct the fiber and sheet
architecture of the heart at a spatial resolution of
3503⫻50⫻800 ␮m, yielding fiber structure estimates at 2
orders of magnitude more points in a fraction of the time
(⬇40 hours versus weeks to months per heart) than can be
achieved histologically.28 We have used these methods to
image and reconstruct the geometry and fiber structure of
populations of normal and failing canine hearts.
Using these imaging data, we have recently developed
computational methods to quantify variation of anatomic
structure both within and between populations of DTI reconstructed hearts.28,29 The method is adapted from the field of
computational anatomy,30,31 whereby different anatomies are
registered to an anatomical template using the large deformation diffeomorphic metric mapping (LDDMM) method.32
Previous computational methods have used low-dimensional
transformations requiring landmarks33 or high-dimensional
transformations but suffer from small deformation assumptions.34,35 LDDMM uses high-dimensional transformation
working under the assumption of large deformations thereby
enabling registration of cardiac pathology that may have large
geometric variation. Similar methods have been used previously to analyze brain structures and their variation in
disease, in particular, to identify deformations in the shape of
the hippocampus that discriminate patients with schizophrenia from matched controls and to define hippocampal shape
and volume abnormalities in patients with mild symptoms of
Alzheimer’s disease.36 Here, we combine, for the first time,
high-resolution diffusion tensor MRI (DTMRI) with rigorous
computational methods to quantify differences in the anatomic structure of a population of normal and dyssynchronous failing canine hearts.
Materials and Methods
Model of Dyssynchronous Heart Failure
The experimental model of cardiac dyssynchrony and heart failure
was generated in canines via radiofrequency ablation of the LBB
followed by 3 weeks of tachypacing (210 minutes⫺1).37,38 This model
has been well described in the literature as 1 that reproduces many of
the molecular, cellular, and structural features of human dilated
cardiomyopathy.39 – 41 Once ventricular dyssynchrony and heart failure were established, animals were euthanized and hearts explanted.
Hearts were retrogradely perfused with a formalin solution and fixed
in an unloaded state before imaging with DTMRI.42 All studies were
conducted in accordance with the guidelines of the Animal Care and
Use Committee of the National Heart, Lung, and Blood Institute.
Diffusion Tensor MRI
Details of the imaging sequence have been reported previously.27,43
Hearts were placed in an acrylic container filled with Fomblin
(Ausimon, Thorofare, NJ), and a 3D Fast Spin-Echo (3D-FSE)
sequence was used to acquire diffusion images. MR parameters
varied slightly depending on heart size. The field of view ranged
from 8 to 10 cm yielding image in-plane resolutions of 312.2⫻312.5
to 390⫻390 ␮m. The volume was imaged with 110 to 120 slices at
800- to 1000-␮m thickness. Diffusion gradients were applied in a
minimum of sixteen noncollinear directions with a maximum diffusion weighting of 1500 s/mm2.
DTI Processing and Ventricular
Fiber/Sheet Analysis
The 3 principal components were computed from the diffusion
tensors at each image voxel.24,26 Voxels in the 3D DTMRI images
representing compact myocardium were identified using a semiautomated contouring method.43 LV geometry was modeled using 3D
FEs, as described by Nielsen et al.23 In the contouring process
endocardial trabeculation was removed from the images, allowing a
smoother description of the geometry and consequently smaller
endocardial fitting errors than those reported by Nielsen et al.23
Diffusion eigenvectors originating from voxels within the FE boundaries were used to study the fiber structure of the ventricles. These
eigenvectors were transformed into the local geometric coordinates
of the model as described by Le Grice et al.44 Fiber angle, ␪, was
defined as the angle formed by the local circumferential tangent
vector and the projection of the primary eigenvector, 1⬘, onto the
epicardial tangent plane, as shown in Figure 2. Using methods
developed previously for the analysis of DTI,27 regions of each heart
exhibiting anisotropic diffusion were identified. The sheet angle, ␾,
(see Figure 2) was computed in these regions, where ␲/2⫹␾ was
defined as the angle formed by the radial vector and the projection of
the tertiary eigenvector 3⬘ into the plane defined by radial and
circumferential vectors.
Anatomical Registration: LDDMM
Anatomical variability is studied by placement of imaged anatomic
structures into standard coordinates using the LDDMM algorithm.29,45 A flow chart and accompanying illustrations shown in
Figure 1 summarize the method. MR images of each heart were
contoured and re-sampled to a common uniform (900 ␮m) lattice. A
normal canine heart from the set of imaged hearts was chosen as an
initial template anatomy (#1 in Figure 1B). Using the LDDMM
algorithm, high-order transformations were computed to register
(green arrows) the template anatomy to the remaining hearts (target
anatomies) such that every voxel in the template heart maps to a
voxel in each target heart. The quality of registration is measured by
the ratio of overlapping image-intensity volumes subsequent to
transformation to that before transformation. The mean trajectory
(red arrow) computed from each mapping (green arrows) is used to
deform the template, defining yet another new template anatomy.
The process is iterated until the mean trajectory length is 0. The
resulting template anatomy is called the Procrustes mean and resides
within the center of possible geometric shapes (Figure 1C).
Geometric variation about this Procrustes mean is studied using
principle component analysis (PCA) of the final mapping trajectories
(green arrows, Figure 1C). In PCA, a set of orthogonal basis vectors
oriented along the directions of maximal variance of the data are
computed.45
Under high-order transformations, such as those computed using
LDDMM, the principle eigenvectors, which define fiber architecture,
are not all preserved.46,47 As a result reorientation of the eigenvectors
must be performed if they are transformed in the mapping. Alternatively, the eigenvectors may be referenced within a geometric
coordinate system, which deforms with the anatomy, thereby elim-
Helm et al
Remodeling in the Dyssynchronous Heart
3
Figure 1. A simplified flow chart (A) and
accompanying illustrations (B and C)
summarizes the computational anatomy
methods. A normal heart was chosen as
an initial template anatomy from a set of
imaged heart structures. Using the
LDDMM, different high-order transformations were computed to map (green
arrows) the template anatomy to the
remaining hearts (target anatomies) (B).
The mean trajectory (red arrow) computed from each mapping (green arrows)
was used to deform the template, defining yet another new template anatomy.
The process was iterated until the mean
trajectory from the template anatomy to
each target heart was 0. At this stage,
the template anatomy resided within the
center of possible geometric shapes (C).
Downloaded from http://circres.ahajournals.org/ by guest on June 18, 2017
inating the need to reorient the eigenvectors. In this report, instead of
performing structure analysis on the eigenvectors in the space of the
template, we use the mapping method to identify corresponding
regions within each nondeformed heart and study fiber/sheet angles
(derived from eigenvectors and referenced in local geometric coordinates) within these regions. For example, within the template
anatomy, an ROI is defined and using the target specific mappings a
corresponding ROI is defined on each target. Structural differences
within a population are observed by comparing fiber angles, within
each corresponding target ROI. Mean values of this pooled information from target ROIs are naturally visualized within the template
ROI.
Geometric Analysis
Referencing geometric images of each target heart into the common
coordinate system of the template, as described above, enables
quantitative comparison of geometric features within corresponding
regions of different imaged hearts. Evaluation of relative wall
thickness (RWT) was performed by comparing corresponding regions in each target heart. The Laplace relation defines wall stress as
being inversely proportional to RWT, defined as the ratio between
wall thickness and chamber radius. RWT provides an indication of
myocyte hypertrophy relative to ventricular dilation and is well
preserved in normal hearts, independent of body weight and ventric-
ular volume.48,49 Epicardial points in the template were identified
and corresponding points in each target were computed using the
LDDMM method. The wall thickness at these points was defined as
the length of the transmural segment between each epicardial point
and the nearest endocardial point. The radius of the ventricle was
determined from a best-fitting circle that encompassed all endocardial points on corresponding slices in each target.
Statistical Analysis
Using the LDDMM method, RWT, fiber and sheet angles within
corresponding regions of each target heart were determined. Statistical significance (P) for geometry was determined using a nonpaired
Student’s t test. Circular statistics50 were used to compute the
circular mean and circular variance of fiber and sheet angles.
Statistical significance for angles was determined using Watson–
Williams F test.50 Probability values ⬍0.01 were considered statistically significant.
Results
LDDMM Matching
Eight normal and 5 failing explanted canine hearts were
imaged using 3D Fast Spin-Echo DTMRI. The average
registration error for matching the template heart to the
normal targets was 5.80⫾1.47% and for matching the template heart to the failing hearts, 4.42⫾0.47%. These values
are not statistically different from each other and are comparable to those reported in the literature for matching of brain
imagery51,52 and demonstrates that the LDDMM method
successfully overlays cardiac target geometries with high
accuracy to a common coordinate system.
Geometric Variability
Figure 2. The coordinate system used to define the fiber angle
␪ and the sheet angle ␾. The fiber angle, ␪, is the angle formed
by the circumferential tangent vector and the projection of the
primary eigenvector, 1⬘, into the epicardial tangent plane. The
sheet angle, ␾, is defined relative to the tertiary eigenvector of
diffusion where ␲/2⫹␾ is the angle formed by the radial vector
and the projection of the tertiary eigenvector, 3⬘, into the plane
defined by radial and circumferential vectors.
The mean geometry for the normal population was computed
using a Procrustes alignment (Figure 1) and used as the
normal template. Regions in the anterior, lateral, posterior,
and septum of this template were selected and corresponding
regions in each target anatomy were identified. RWT within
corresponding regions at the base and apex are shown in the
Table. The normal population showed an average RWT of
0.52⫾0.04 with no statistical difference over the entire
4
Circulation Research
January 6/20, 2006
RWT (ⴛ100) Measurements for Various Regions Within the LV of Normal and Failing Canine
Hearts
Basal
Anterior
Basal
Lateral
Basal
Posterior
Normal
(n⫽8)
50⫾3
51⫾3
50⫾3
49⫾4
Failing
(n⫽5)
40⫾6†
42⫾7†
37⫾7†
29⫾6*†
RWT⫻100
Basal
Septal
Apical
Anterior
57⫾10
41⫾8†
Apical
Lateral
51⫾11
32⫾5*†
Apical
Posterior
Apical
Septal
49⫾9
64⫾14†
29⫾6*†
41⫾20
†Statistical significance (P⬍0.01) relative to basal lateral wall of normal population. Within in the failing population,
* denotes statistical significance (P⬍0.01) relative to basal lateral wall.
Downloaded from http://circres.ahajournals.org/ by guest on June 18, 2017
ventricle except for the apical septum. Within the apical
septum, the RWT was larger at 0.61⫾0.04. This difference
may be attributed to the errors associated with identifying the
RV endocardial surface given the extent of trabeculation
within the RV apex. The failing population showed a significant reduction of this ratio, indicating a greater ventricular
dilation relative to myocyte hypertrophy. There was also
significant regional disparity of this ratio. RWT within the
lateral region was significantly different (P⬍0.01) than that
found in the septal wall, (0.42⫾0.07 and 0.29⫾0.06, respectively). Regional disparity was not as evident in the apical
regions. Differences in RWT between the normal and failing
populations are depicted in Figure 3. The top row (Figure 3A)
shows the template heart (in anterior/posterior view and 2
cut-away perspectives) colored according to mean RWT for
the normal population. The middle row (Figure 3B) shows the
template heart colored according to mean RWT for the failing
population. Regional disparity is clearly evident. The statistical differences between normal and failing populations are
shown graphically in the bottom row (Figure 3C). The
template heart is colored such that regional differences that
are statistically significant (P⬍0.01) are blue and regional
differences that are not significant are cyan.
We next examined geometric variability of the normal
population about the normal template using PCA applied to
the mapping trajectories defined from the template anatomy.
Analyses were limited to assessment of the principal eigenvector ␣n, (ie, direction of highest geometric variability).
Figure 4 shows different time steps in the evolution of the
normal template (middle top image) in the direction of ␣n (top
right) and ⫺␣n (top left). The insertion of the RV shows the
greatest variability in the normal population. There is some
septal wall deviation, which may be attributable in part to
variability in the RV insertion. Figure 4 also shows evolution
of the normal template (middle bottom image) in the principal
direction of highest variation for the failing population, ␣f. As
expected, the most notable variation was dilation of the left
ventricular chamber and reduction of wall thickness. Movies
showing the deformation of the template heart in the direction
of highest geometric variance for both normal and failing
populations are available in the online data supplement at
http://circres.ahajournals.org.
Fiber Structure Variability
Before studying diffusion eigenvectors, a ventricular coordinate system from which fiber and sheet angles are referenced
was defined. On average, each MR study resulted in 50 000
epicardial and 27 000 LV endocardial data points to which
the radial component of a 24-element prolate spheroidal FE
mesh was fit. The average root mean squared errors of the FE
fit on epicardial and left ventricular endocardial surface were
0.81⫾1.08 mm and 0.68⫾0.83 mm, respectively. Fiber and
sheet angles were determined from the primary and tertiary
eigenvectors using the ventricular coordinate system as
shown in Figure 2. On average, each study resulted in
550 000 measurements of fiber and sheet angle within the
myocardium.
Plots of mean fiber angle in the normal and failing hearts
are shown in Figure 5. The top row (Figure 5A) shows the
Figure 3. The top row (A) shows the template heart (3 different
views) colored according to the mean RWT for the normal population. The middle row (B) shows the template heart color
according to the mean RWT for the failing population. Note the
reduced thickness in the septal wall. The RV (gray) was not analyzed but included in the figure for a reference. The bottom row
(C) shows the statistical difference (p) as determined by the Student’s t test between the normal and failing population. The
color cyan represents no difference and the color blue represents a statistical difference at (P⬍0.01).
Helm et al
Remodeling in the Dyssynchronous Heart
5
Figure 4. With ␣n defined as a vector
pointing in the direction of highest geometric variance of a population on normals (see Materials and Methods), we
illustrate the evolution of normal template (middle top image) in the direction
of ␣n (top right) and ⫺␣n (top left). The
insertion of RV (gray arrows) shows
highest variability in the normal population. There is some septal wall deviation
(gray arrows) mostly attributable to the
variability in RV insertion. In the bottom
row, we illustrate the evolution of the
normal template in the principal direction
of highest geometric variance, ␣f, for the
failing population. Changes occurred in
the LV diameter (gray arrows), wall thickness, and expanse of the septal wall.
Downloaded from http://circres.ahajournals.org/ by guest on June 18, 2017
template heart colored according to mean fiber angle for the
normal population, whereas the middle row (Figure 5B)
shows the template heart colored according to average fiber
angle for the failing population. The bottom row (Figure 5C)
displays the statistical significance of regional differences in
fiber orientation between the normal and failing hearts.
Despite large regional differences in wall thickness in the
septal and lateral walls, the majority of the LV showed no
significant change in fiber structure. Some regions on the
epicardial and endocardial surfaces showed an increase in
fiber angle for the failing population as noted in yellowish
color, but these differences were not significant at P⬍0.01.
These data therefore demonstrate that fiber orientation assessed at corresponding points in failing and control hearts
are largely similar.
Laminar Structure Variability
Variability of laminar structure was also studied. The top row
(Figure 6A) shows the template heart colored according to
dominant sheet angles for the normal population. Two dominant populations of sheet angles were identified: 1 at
approximately ⫺45° and the other at ⫹45°. The majority of
the lateral wall (both apex and base) showed a single
dominant angle at approximately ⫺45°, whereas the majority
of the septum showed a dominant angle of ⫹45° at the base
and ⫺45° at the apex. Transmural variation in the dominant
angles is also seen in some LV regions as the angles toggled
from ⫺45 to ⫹45 and sometimes back (lateral wall). A
statistical assessment of differences in laminar structure
between normal and failing hearts is shown in the bottom
(Figure 6C) set of images. The majority of the LV showed no
significant difference between the laminar structure in the
normal and failing populations; however, in the septal region
of the failing heart, both population of sheet angles (⫾45)
became steeper (less radial) by approximately 15°. These
differences were statistically significant (P⬍0.01).
Discussion
Figure 5. The top row (A) shows the template heart (3 different
views) colored according to average fiber angle (degrees) for the
normal population. The middle row (B) shows the template heart
color according to average fiber angle for the failing population.
There is a very slight increase in fiber angles on the epicardial
and endocardial surface for the failing heart as noted by the
more yellow/red color on these surfaces. The bottom row (C)
shows the statistical difference between the normal and failing
population. The color cyan represents no difference and the
color blue represents a statistical difference at (P⬍0.01).
To our knowledge, this is the first report that combines high
resolution diffusion tensor imaging techniques with methods
of computational anatomy to demonstrate quantitatively
global and local remodeling in a population of normal and
failing hearts with a LBBB. There are several important
findings.
First, our results show regional differences in anatomical
remodeling in the dyssynchronous failing heart. Significant
ventricular chamber dilatation and reduction of RWT in
septal, posterior, and anterior regions was observed, whereas
the lateral wall showed little change in RWT. It has been
shown previously that the tachycardia-induced heart failure
model leads to greater ventricular dilation relative to ventric-
6
Circulation Research
January 6/20, 2006
Downloaded from http://circres.ahajournals.org/ by guest on June 18, 2017
Figure 7. Shown is an illustration of sheet remodeling that
accounts for reduction in wall thickness. Shown in A are normal
sheet orientation and B, altered sheet orientation. The sheets
become more vertical (less radial) and hence the wall becomes
thinner.
Figure 6. The top row (A) shows the template heart (3 different
views) colored according to sheet angle (degrees) for the normal
population. The middle row (B) shows the template heart color
according to sheet angle (degrees) for the failing population.
The bottom row (C) shows the statistical difference between the
normal and failing population. The color cyan represents no difference and the color blue represents a statistical difference at
(P⬍0.01).
ular mass41; hence, RWT should reduce as compared with
normal hearts. We observed a similar global reduction in
RWT as a result of tachycardia pacing. However, our model
additionally includes a LBB block. Such dyssynchronous
electrical activation results in early and late mechanical
activated regions of myocardium and hence subjects these
regions to different loading conditions. In early systole, the
late-activated lateral wall dilates (stretches) because of contraction of the early-activated septum. A reversal of this effect
occurs during late systole/early diastole when the lateral wall
contracts against a relaxing septum. These regional differences in wall stress ultimately lead to different patterns of
hypertrophy/remodeling as we observed. Prinzen et al
showed similar differences in hypertrophy response in earlyactivated versus late-activated myocardium using ventricular
pacing studies.53
Second, despite regional differences in gross remodeling,
fiber orientation at corresponding points remains similar in
control versus failing hearts. These results are consistent with
other canine models of failure induced with arteriovenous
fistule. Such studies indicate global dilation with little change
in fiber orientation.1,54 These results, coupled with gross
remodeling of wall thickness (particularly in the septum),
imply a statistically significant change in transmural fiber
gradient. Given that the gradient of fiber orientation is a
major determinant of electrical propagation,55 this has important implications for electrical activation of the ventricle.
Finally, we demonstrate significant (P⬍0.01) regional
difference in sheet structure remodeling that may explain
regional difference in wall thickness. Specifically, we find an
increase of sheet angle in the early-activated septum but no
change in that of the late-activated lateral wall. These data
imply a possible slowing of transmural electrical conduction,
because conductivity is smaller in the cross-sheet direction. A
possible mechanism of remodeling occurring in the septum is
shown graphically for a small transmural tissue slab in Figure
7. The normal sheet structure is shown in Figure 7A. As sheet
angle ␾ increases, the laminar sheets assume a more vertical
orientation, thus reducing overall wall thickness (Figure 7B).
This mechanism has been proposed and substantiated by
others.54 Such reorientation also implies an elongation of the
septal wall, which is observable in Figure 4. Unlike the lateral
wall, the septal wall showed large variation in its apex to base
arc length. We observed no significant changes in the laminar
architecture of the lateral wall.
These data have important clinical implications. Mechanical dyssynchrony is common in patients with dilated cardiomyopathy, ventricular pacemakers and/or post–myocardial
infarction. Our data shows regional differences in remodeling
in the dyssynchronous failing heart particularly within the
laminar sheet structure. Sheet structure influences the apparent passive properties of myocardium; thus regional differences in sheet structure may impart heterogeneity of myocardial function within the ventricle. Although it is yet unclear
whether these structural changes coupled with altered electrical conduction attributable to increased fiber gradient are
beneficial or detrimental to function, a better appreciation of
the remodeling process is important in the understanding of,
improvement in, and development of therapeutics.
In conclusion, unlike previous studies of myofiber architecture, we have used a high-resolution, 3D imaging modality
coupled with rigorous mathematical assessment of variability
to demonstrate significant regional changes in ventricular
structure in the dyssynchronous, failing heart, thereby en-
Helm et al
abling quantitative understanding of the nature of ventricular
remodeling and heart failure progression
Acknowledgments
This work was supported by NIH grants HL70894 and HL52307,
Natural Sciences and Engineering Research Council of Canada grant
31-611387, the Falk Medical Trust, and IBM Corporation. D.B.E.
was supported by a pre-IRTA fellowship from the National Heart,
Lung, and Blood Institute.
References
Downloaded from http://circres.ahajournals.org/ by guest on June 18, 2017
1. Omens JH, Covell JW. Transmural distribution of myocardial tissue
growth induced by volume-overload hypertrophy in the dog. Circulation. 1991;84:1235–1245.
2. Grossman W, Jones D, McLaurin LP. Wall stress and patterns of hypertrophy in the human left ventricle. J Clin Invest. 1975;56:56 – 64.
3. Grossman W. Cardiac hypertrophy: useful adaptation or pathologic
process? Am J Med. 1980;69:576 –584.
4. Murkofsky RL, Dangas G, Diamond JA, Mehta D, Schaffer A, Ambrose
JA. A prolonged QRS duration on surface electrocardiogram is a specific
indicator of left ventricular dysfunction. J Am Coll Cardiol. 1998;32:
476 – 482.
5. Wilensky RL, Yudelman P, Cohen AI, Fletcher RD, Atkinson J, Virmani
R, Roberts WC. Serial electrocardiographic changes in idiopathic dilated
cardiomyopathy confirmed at necropsy. Am J Cardiol. 1988;62:276 –283.
6. Grimm W, Sharkova J, Funck R, Maisch B. How many patients with
dilated cardiomyopathy may potentially benefit from cardiac resynchronization therapy? Pacing Clin Electrophysiol. 2003;26:155–157.
7. Leclercq C, Faris O, Tunin R, Johnson J, Kato R, Evans F, Spinelli J,
Halperin H, McVeigh E, Kass DA. Systolic improvement and mechanical
resynchronization does not require electrical synchrony in the dilated
failing heart with left bundle-branch block. Circulation. 2002;106:
1760 –1763.
8. Grines CL, Bashore TM, Boudoulas H, Olson S, Shafer P, Wooley CF.
Functional abnormalities in isolated left bundle branch block. The effect
of interventricular asynchrony. Circulation. 1989;79:845– 853.
9. Xiao HB, Lee CH, Gibson DG. Effect of left bundle branch block on
diastolic function in dilated cardiomyopathy. Br Heart J. 1991;66:
443– 447.
10. Nelson GS, Curry CW, Wyman BT, Kramer A, Declerck J, Talbot M,
Douglas MR, Berger RD, McVeigh ER, Kass DA. Predictors of systolic
augmentation from left ventricular preexcitation in patients with dilated
cardiomyopathy and intraventricular conduction delay. Circulation. 2000;
101:2703–2709.
11. Thambo JB, Bordachar P, Garrigue S, Lafitte S, Sanders P, Reuter S,
Girardot R, Crepin D, Reant P, Roudaut R, Jais P, Haissaguerre M,
Clementy J, Jimenez M. Detrimental ventricular remodeling in patients
with congenital complete heart block and chronic right ventricular apical
pacing. Circulation. 2004;110:3766 –3772.
12. Yu CM, Chau E, Sanderson JE, Fan K, Tang MO, Fung WH, Lin H, Kong
SL, Lam YM, Hill MR, Lau CP. Tissue Doppler echocardiographic
evidence of reverse remodeling and improved synchronicity by simultaneously delaying regional contraction after biventricular pacing therapy
in heart failure. Circulation. 2002;105:438 – 445.
13. St John Sutton MG, Plappert T, Abraham WT, Smith AL, DeLurgio DB,
Leon AR, Loh E, Kocovic DZ, Fisher WG, Ellestad M, Messenger J,
Kruger K, Hilpisch KE, Hill MR. Effect of cardiac resynchronization
therapy on left ventricular size and function in chronic heart failure.
Circulation. 2003;107:1985–1990.
14. Abraham WT, Fisher WG, Smith AL, Delurgio DB, Leon AR, Loh E,
Kocovic DZ, Packer M, Clavell AL, Hayes DL, Ellestad M, Trupp RJ,
Underwood J, Pickering F, Truex C, McAtee P, Messenger J. Cardiac
resynchronization in chronic heart failure. N Engl J Med. 2002;346:
1845–1853.
15. Fox CC, Hutchins GM. The architecture of the human ventricular myocardium. Johns Hopkins Med J. 1972;130:289 –299.
16. MacCallum J. On the muscular architecture and growth of the ventricles
of the heart. Johns Hopkins Hosp Rep. 1900;9:307–335.
17. Mall F. On the muscular architecture of the ventricles of the human heart.
Am J Anat. 1911;11:211–266.
18. Ross J Jr, Sonnenblick EH, Taylor RR, Spotnitz HM, Covell JW. Diastolic geometry and sarcomere lengths in the chronically dilated canine
left ventricle. Circ Res. 1971;28:49 – 61.
Remodeling in the Dyssynchronous Heart
7
19. Streeter DD Jr, Spotnitz HM, Patel DP, Ross J Jr, Sonnenblick EH. Fiber
orientation in the canine left ventricle during diastole and systole. Circ
Res. 1969;24:339 –347.
20. Streeter DD Jr. Gross morphology and fiber geometry of the heart. In:
Berne RM, Sperelakis N, Geiger SR, eds. Handbook of Physiology,
Section 2: The Cardiovascular System. Vol 1. Bethesda, Md: American
Physiological Society; 1979:61–112.
21. Le Grice IJ, Smaill BH, Chai LZ, Edgar SG, Gavin JB, Hunter PJ,
Takayama Y, Covell JW. Laminar structure of the heart: ventricular
myocyte arrangement and connective tissue architecture in the dog. Am J
Physiol. 1995;269:H571–H582.
22. Costa KD, Takayama Y, McCulloch AD, Covell JW. Laminar fiber
architecture and three-dimensional systolic mechanics in canine ventricular myocardium. Am J Physiol. 1999;276:H595–H607.
23. Nielsen PM, Le Grice IJ, Smaill BH, Hunter PJ. Mathematical model of
geometry and fibrous structure of the heart. Am J Physiol. 1991;260:
H1365–H1378.
24. Basser PJ, Mattiello J, LeBihan D. Estimation of the effective selfdiffusion tensor from the NMR spin echo. J Magn Reson B. 1994;103:
247–254.
25. Hsu EW, Muzikant AL, Matulevicius SA, Penland RC, Henriquez CS.
Magnetic resonance myocardial fiber-orientation mapping with direct
histological correlation. Am J Physiol. 1998;274:H1627–H1634.
26. Scollan DF, Holmes A, Winslow R, Forder J. Histological validation of
myocardial microstructure obtained from diffusion tensor magnetic resonance imaging. Am J Physiol. 1998;275:H2308 –H2318.
27. Helm PA, Tseng HJ, Younes L, McVeigh E, Winslow RL. Ex vivo 3D
diffusion tensor imaging and quantification of cardiac laminar structure.
Magn Reson Med. 2005;54:850 – 859.
28. Helm PA, Beg MF, Miller MI, Winslow RL. Measuring and mapping
cardiac fiber and laminar architecture using diffusion tensor MR imaging.
Ann N Y Acad of Sci. 2005;1047:296 –307.
29. Beg MF, Helm PA, McVeigh E, Miller MI, Winslow RL. Computational
cardiac anatomy using MRI. Magn Reson Med. 2004;52:1167–1174.
30. Grenander U, Miller MI. Computational anatomy: an emerging discipline.
Quart Appl Math. 1998;56:617– 694.
31. Miller MI, Trouve A, Younes L. On the metrics and euler-lagrange
equations of computational anatomy. Annu Rev Biomed Eng. 2002;4:
375– 405.
32. Beg MF, Miller MI, Trouve A, Younes L. Computing metrics via geodesics on flows of diffeomorphisms. Int J Comput Vis. 2005;61:139 –157.
33. Pelizzari CA, Chen GT, Spelbring DR, Weichselbaum RR, Chen CT.
Accurate three-dimensional registration of CT, PET, and/or MR images
of the brain. J Comput Assist Tomogr. 1989;13:20 –26.
34. Dann R, Hoford J, Kovacic S, Reivich M, Bajcsy R. Evaluation of elastic
matching system for anatomic (CT, MR) and functional (PET) cerebral
images. J Comput Assist Tomogr. 1989;13:603– 611.
35. Evans AC, Marrett S, Neelin P, Collins L, Worsley K, Dai W, Milot S,
Meyer E, Bub D. Anatomical mapping of functional activation in stereotactic coordinate space. Neuroimage. 1992;1:43–53.
36. Csernansky JG, Joshi S, Wang L, Haller JW, Gado M, Miller JP,
Grenander U, Miller MI. Hippocampal morphometry in schizophrenia by
high dimensional brain mapping. Proc Natl Acad Sci U S A. 1998;95:
11406 –11411.
37. Armstrong PW, Stopps TP, Ford SE, de Bold AJ. Rapid ventricular
pacing in the dog: pathophysiologic studies of heart failure. Circulation.
1986;74:1075–1084.
38. Coleman HN 3rd, Taylor RR, Pool PE, Whipple GH, Covell JW, Ross J
Jr, Braunwald E. Congestive heart failure following chronic tachycardia.
Am Heart J. 1971;81:790 –798.
39. Kaab S, Nuss HB, Chiamvimonvat N, O’Rourke B, Pak PH, Kass DA,
Marban E, Tomaselli GF. Ionic mechanism of action potential prolongation in ventricular myocytes from dogs with pacing-induced heart
failure. Circ Res. 1996;78:262–273.
40. Williams RE, Kass DA, Kawagoe Y, Pak P, Tunin RS, Shah R, Hwang
A, Feldman AM. Endomyocardial gene expression during development
of pacing tachycardia-induced heart failure in the dog. Circ Res. 1994;
75:615– 623.
41. Wilson J, Douglas P, Hickey W, Lanoce V, Ferraro N, Muhammad A,
Reichek N. Experimental congestive heart failure produced by rapid
ventricular pacing in the dog: cardiac effects. Circulation. 1987;75:
857– 867.
42. Faris OP, Evans FJ, Ennis DB, Helm PA, Taylor JL, Chesnick AS,
Guttman MA, Ozturk C, McVeigh ER. Novel technique for cardiac
8
43.
44.
45.
46.
47.
48.
49.
Circulation Research
January 6/20, 2006
electromechanical mapping with magnetic resonance imaging tagging
and an epicardial electrode sock. Ann Biomed Eng. 2003;31:430 – 440.
Scollan DF, Holmes A, Zhang J, Winslow RL. Reconstruction of cardiac
ventricular geometry and fiber orientation using magnetic resonance
imaging. Ann Biomed Eng. 2000;28:934 –944.
Le Grice IJ, Hunter PJ, Smaill BH. Laminar structure of the heart: a
mathematical model. Am J Physiol. 1997;272:H2466 –H2476.
Vaillant M, Miller MI, Younes L, Trouve A. Statistics on diffeomorphisms via tangent space representations. Neuroimage. 2004;23(suppl
1):S161–S169.
Alexander DC, Pierpaoli C, Basser PJ, Gee JC. Spatial transformations of
diffusion tensor magnetic resonance images. IEEE Trans Med Imaging.
2001;20:1131–1139.
Cao Y, Miller M, Winslow R, Younes L. Large deformation diffeomorphic metric mapping of vector fields. IEEE Trans Med Imaging.
2005;24:1216 –1230.
Bennett DH, Evans DW, Raj MV. Echocardiographic left ventricular
dimensions in pressure and volume overload. Their use in assessing aortic
stenosis. Br Heart J. 1975;37:971–977.
Gaasch WH. Left ventricular radius to wall thickness ratio. Am J Cardiol.
1979;43:1189 –1194.
50. Mardia KV. Statistics of Directional Data. New York: Academic Press
Inc; 1972.
51. Christensen GE, Rabbitt RD, Miller MI. 3D brain mapping using a
deformable neuroanatomy. Phys Med Biol. 1994;39:609 – 618.
52. Haller JW, Banerjee A, Christensen GE, Gado M, Joshi S, Miller MI,
Sheline Y, Vannier MW, Csernansky JG. Three-dimensional hippocampal MR morphometry with high-dimensional transformation of a
neuroanatomic atlas. Radiology. 1997;202:504 –510.
53. Prinzen FW, Cheriex EC, Delhaas T, van Oosterhout MF, Arts T, Wellens
HJ, Reneman RS. Asymmetric thickness of the left ventricular wall
resulting from asynchronous electric activation: a study in dogs with
ventricular pacing and in patients with left bundle branch block. Am
Heart J. 1995;130:1045–1053.
54. Ashikaga H, Omens JH, Covell JW. Time-dependent remodeling of
transmural architecture underlying abnormal ventricular geometry in
chronic volume overload heart failure. Am J Physiol Heart Circ Physiol.
2004;287:H1994 –H2002.
55. Roberts DE, Hersh LT, Scher AM. Influence of cardiac fiber orientation
on wavefront voltage, conduction velocity, and tissue resistivity in the
dog. Circ Res. 1979;44:701–712.
Downloaded from http://circres.ahajournals.org/ by guest on June 18, 2017
Evidence of Structural Remodeling in the Dyssynchronous Failing Heart
Patrick A. Helm, Laurent Younes, Mirza F. Beg, Daniel B. Ennis, Christophe Leclercq, Owen P.
Faris, Elliot McVeigh, David Kass, Michael I. Miller and Raimond L. Winslow
Downloaded from http://circres.ahajournals.org/ by guest on June 18, 2017
Circ Res. published online December 8, 2005;
Circulation Research is published by the American Heart Association, 7272 Greenville Avenue, Dallas, TX 75231
Copyright © 2005 American Heart Association, Inc. All rights reserved.
Print ISSN: 0009-7330. Online ISSN: 1524-4571
The online version of this article, along with updated information and services, is located on the
World Wide Web at:
http://circres.ahajournals.org/content/early/2005/12/08/01.RES.0000199396.30688.eb.citation
Data Supplement (unedited) at:
http://circres.ahajournals.org/content/suppl/2005/12/08/01.RES.0000199396.30688.eb.DC1
Permissions: Requests for permissions to reproduce figures, tables, or portions of articles originally published
in Circulation Research can be obtained via RightsLink, a service of the Copyright Clearance Center, not the
Editorial Office. Once the online version of the published article for which permission is being requested is
located, click Request Permissions in the middle column of the Web page under Services. Further information
about this process is available in the Permissions and Rights Question and Answer document.
Reprints: Information about reprints can be found online at:
http://www.lww.com/reprints
Subscriptions: Information about subscribing to Circulation Research is online at:
http://circres.ahajournals.org//subscriptions/