Download ENEE 313, Spr. `09 Midterm I Solutions

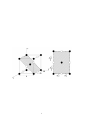
ENEE 313, Spr. ’09 Midterm I Solutions
PART I—CRYSTALS, 25 pts.
1. Consider the crystal whose unit cell is given in the figure below. The black atoms are type A and
the white atoms are type B.
(a) (8 pts.) How many total atoms are there per unit cell?
There are eight corner atoms, each shared between eight unit cells; four edge atoms,
each shared between four unit cells, two face atoms, each shared between two unit
cells, and one body-center atom which is not shared. Therefore there are a total of
(1/8)x8+(1/4)x4+(1/2)x2+1=4 atoms per unit cell.
(b) (10 pts.) What is the distance between the nearest neighboring atoms of either type (A or B)
in the (011) plane? (Show the plane.)
The plane is shown in the figure below, with a top-down (normal-angle) view added on
the side
√ for convenience. From this, we can see that the nearest neighboring A atoms
are a 3/2 apart, as are the nearest neighboring B atoms, while the shortest distance
between any atoms are a/2.
(c) (7 pts.) This crystal is built based on a body-centered cubic lattice. What is the basis used to
obtain this unit cell?
There are several possible valid basis choices which would give this unit cell from the BCC
lattice. One possibility is “an A atom at every lattice point and a B atom x̂/2 away.”
(d) (BONUS: 5 pts.) Assume atoms of both types have the same radius and the nearest neighbors
in this unit cell are touching. Find the packing fraction of the unit cell.
The nearest neigbors in the cell are a/2 apart; therefore the atomic radius has to be a/4.
Therefore
Vatom
Vunitcell
⇒ Packing fraction
1
4 3
4πa3
πa3
=
πr =
=
3
3 × 43
48
= a3
4 × (πa3 /48)
π
=
=
3
a
12
2
PART II—QUANTUM PHYSICS, 25 pts.
2. Consider infinite potential well shown in the figure, where
the potential energy V goes to infinity at x = 0 and x = 2L:
(a) (5 pts.) Write the Time-Independent Schroedinger Wave Equation in the well region (0 < x <
2L) to find the wavefunction ψ(x) associated with a particle with mass m in this potential well.
In the well, the potential energy V (x) = 0. Therefore the TISWE is:
d2 ψ(x) 2m
+ 2 Eψ(x) = 0
dx2
h̄
(1)
(b) (5 pts.) Write the boundary conditions and the normalization condition for the time-independent
wavefunction ψ(x), which is the solution of the TI SWE. (Hint: The time-dependent part of the
solution will cancel out of the normalization integration, so does not need to be considered.)
B oundary conditions:
At x = 0
At x = 2L
:
:
ψ(0) = 0 ;
ψ(2L) = 0
N ormalization condition:
Z 2L
∗
ψ (x)ψ(x)dx =
Z 2L
ψ 2 (x)dx = 1
0
0
(2)
(c) (7 pts.) Solve the TI SWE using the boundary conditions and the normalization condition. To
simplify the equation, use the definition k 2 = (2mE)/h̄2 and find the allowed values of k. Note
that you will obtain a series of discretized wavefunctions, with the integer parameter n. Use the
n = 1 wavefunction for normalization.
Z a
(Hint :
0
sin2 (
πx
)dx = a/2 for any constant a.)
a
3
Rewrite the TISWE and use the k definition given:
d2 ψ(x)
2m
= − 2 Eψ(x)
2
dx
h̄
2
2
⇒ d ψ(x)dx = −k 2 ψ(x)
⇒ ψ(x) = A sin (kx) + B cos (kx)
Using the x = 0 boundary condition, we deduce that B = 0.
Using the x = 2L boundary condition, we deduce that k = nπ/(2L), where n is 1, 2, 3 ...
Then we use the normalization condition and the n = 1 to find A:
Z 2L
ψ 2 (x)dx = 1
0
⇒ A2
Z 2L
πx
)dx = 1
2L
⇒ A = 1/L
πx
1
sin ( )
⇒ ψ1 (x) =
L
2L
sin2 (
0
(d) (4 pts.) Find the average momentum < p > of the particle in the ground state n = 1 using the
momentum operator
p̂ = −ih̄
∂
∂x
√
where i = −1. (Hint: sin (ax) cos (ax) = sin (2ax)/2; once again, the time-dependent part of
the wavefunction will cancel out.)
Using the integral given in the equation list with the momentum operator:
<p> =
Z
Ψ∗ (x, t)(−ih̄
= −ih̄
Z
ψ(x)
∂ ∗
[Ψ (x, t)]dx
∂x
∂
[ψ(x)]dx
∂x
and the integral given in the hint, we find that the average momentum < p > is zero.
(e) (4 pts.) Qualitatively compare the probabilities of finding the particle in the region 0.95 L < x < 1.05 L
for the particle in the ground state (n = 1) and the next higher state (n = 2). (Hint: Sketch
the wavefunctions and consider the probability density functions for these two states.)
Comparing the area for the probabilty density functions (|ψ(x)|2 ) for these two states in
the figure on the next page, it is clear that the probability for the n = 2 state for finding
the particle in the region 0.95 L < x < 1.05 L is higher:
(f) (BONUS: 5 pts.) We know that the particle in any of the states of the infinite potential well
has to have a nonzero kinetic energy, and therefore nonzero momentum. Why is the result of
part d) not inconsistent with this statement?
4
The particle in any state will have a positive kinetic energy and therefore nonzero momentum; however, it is equally likely to be moving in the −x̂ direction as in the x̂ direction.
Therefore the average momentum, if you look at many particles in this state of many
wells, comes out to zero.
5
PART III—CARRIERS IN SEMICONDUCTORS, 35 pts.
3. In this question, consider two semiconductor materials, Aa and Bb. The band-symmetry approximation holds for both materials; that is to say, NC,Aa = NV,Aa and NC,Bb = NV,Bb where NC and
NV are the effective density of states for the conduction and valence bands, respectively.
(a) (5 pts.) Assume NC,Aa = 1.5NC,Bb and Eg,Aa = 0.5Eg,Bb , where Eg is the bandgap energy
of the material. At the same temperature T1 , which material has the higher intrinsic carrier
concentration ni ? Show your reasoning.
Since NC = NV , we can write the intrinsic carrier concentration for either semiconductor
as
q
−Eg
NC2 exp (
)
ni =
2kT
−Eg
)
= NC exp (
2kT
Then, for these materials:
−0.5Eg,Bb
ni,Aa = 1.5NC,Bb exp (
)
2kT
−Eg,Bb
= 1.5NC,Bb exp (
)
4kT
−Eg,Bb
ni,Bb = NC,Bb exp (
)
2kT
⇒ ni,Aa > ni,Bb
This makes sense, since Aa has both a higher density of states than Bb, and a smaller
bandgap that makes it easier for EHPs to be generated.
(b) (5 pts.) Now assume NC,Aa = NC,Bb and Eg,Aa = 0.5Eg,Bb . If the temperature is raised to
2T1 , which material experiences the larger change in ni ? Show your reasoning.
Define NC = NC,Aa = NC,Bb . Then you can calculate the intrinsic carrier concentration
for each material at T1 and 2T1 and compare. It seems that the ratio of ni at 2T1 to
that at T1 is higher for Bb; however if you look at the absolute change |ni (2T1 ) − ni (T1 )|,
ni,Aa changes more by orders of magnitude, since its lower bandgap makes its carrier
concentration and bandgap much more sensitive to temperature changes.
4. Consider a silicon sample doped uniformly with donor atoms, so that ND = 2 × 1016 1/cm3 . Use
Eg =1.12 eV for the bandgap.
(a) (10 pts.) Find n0 , p0 and the location of EF in the bandgap at room temperature (300 ◦ K) at
equilibrium. Sketch the band energy diagram; mark EC , EV , Ei and EF .
The sample only has donor atoms; therefore it is n-type. So:
n0 ≈ ND = 2 × 1016 1/cm3
n2i
p0 =
= 1.05 × 104 1/cm3
n0
kT
n0
(Ei − EF ) =
ln ( ) = 0.368 eV
q
ni
6
(b) (8 pts.) Assume the mean-free time τf is the same for electrons and holes. Assume that the
effective mass of holes is three times that of electrons, and assume µn =1500 cm2 /V.sec is the
electron mobility. What are the conductivity due to electrons and the conductivity due to holes
at equilibrium at 300 ◦ K? Write the net drift current density in terms of an applied electric field
E.
m∗n = m∗p /3 ⇒ µp = µn /3 = 500 cm2 /V.sec
σn = qµn n0 = 1.6 × 10−19 × 1500 × 2 × 1016 = 4.8 1/Ω.cm
σp = 1µp p0 = 1.6 × 10−19 × 500 × 10500 = 8.4 × 10−13 1/Ω.cm
Jnet,drif t = Jn,drif t + Jp,drif t ≈ Jn,drif t = σn E = 4.8E A/cm2
since in this case we can almost ignore the hole drift current with respect to the electron
drift current.
(c) (7 pts.) Suggest a possible acceptor density NA to add to this sample so that the conductivities
due to both carrier types become comparable (for instance, the lesser is no less than 1/100th of
the greater). Show your work.
Let’s start by choosing a target conductivity; for example, σp = σn /30. Because of the
mobility ratio, this implies that we need p = 3n: The new material will be p-type. Thus
we have the following equations to solve for p and n, and thus for NA :
p = 3n
n2
n= i
p
⇒p
⇒ NA
= NA − ND
n2
ni
⇒ n = i ⇒ n = √ = 8.37 × 109 1/cm3
3n
3
10
3
= 2.15 × 10 1/cm
= ND + 2.15 × 1010 = 2.00000215 × 1016 1/cm3
So to get the minority and majority carrier concentrations to be comparable, which is
required to get the minority and majority conductivities to be comparable, the added
acceptor density needs to be quite close to the added donor density.
7
Part IV—15 pts.
5. Fill in the blanks, choose the correct statement or indicate “True” or “False” for the statements
below. Each blank, true/false or multiple choice answer is worth one point. Blanks might contain
more than one word. You may choose 15 to answer; if you get more than 15 answers right
in this section your grade will be 15.
(a) Increasing the intensity of light falling on a metal increases the number of photoelectrons
emitted, but only if the frequency the light is high enough.
(b) One of Bohr’s postulates implies that the diameter of a stable orbit around the atomic nucleus
has to be an integer multiple of the associated wavelength OR de Broglie wavelength of
the electron there.
(c) Electrons in a semiconductor crystal contribute to conduction only if their energy level falls into
the conduction band..
(d) Multiple Choice: In Part I, Question 1 of this test, the crystal surface with the highest number
of type A atoms in the unit cell volume is— (a) (010), (b) (110), (c) (111) .
(e) True/False: Blue light at λ = 250 nm can create electron-hole pairs in intrinsic silicon carbide,
with bandgap 3.26 eV: TRUE
(f) True/False: If a p-type material is doped with additional acceptors, the Fermi level gets closer
to the conduction band: FALSE
(g) A crystal can be formed by placing a basis (an arrangement of atoms) at each lattice point.
(h) If the curvature of the E −k relationship of the conduction band of a material in a given direction
in the crystal is gentler than the curvature in another direction, the electron effective mass is
higher in the first direction.
(i) Acceptors are impurities that have a free bond OR valence state OR state able to accept
an electron when placed in a semiconductor lattice.
(j) True/False: In a p-type semiconductor, (1 − f (EV )) < f (EC ): FALSE
(k) In an extrinsic semiconductor doped with acceptors, electrons are the minority carriers.
(l) Rate of recombination increases with increasing carrier concentration if the system is not at
equilibrium, but if no external sources are present, rate of generation stays constant as long
as temperature is unchanged.
(m) Multiple choice Which one of the following is a valid (n, l, m) triplet for the quantum numbers
of an electron bound to an atom? (a) (2,3,0) (b) (1,0,-1) (c) (4,2,-2) (d) (3,3,-1)
(n) Multiple choice The energy of an electron in orbit around the hydrogen atom comes from the solution to the ......-dependent equation obtained by using separation of variables on the Schroedinger
equation. (a) θ (b) φ (c) r
(o) The diamond lattice has 4 lattice points that are enclosed entirely within the unit cell.
8