Download NOISE - ecsa ekc

Analog
Communication
Module 4
NOISE
P. Suresh Venugopal
Analog Communication - NOISE
2
Topics to be covered
• Noise
– Sources of noise
• Thermal Noise, Shot Noise, Flicker noise and White noise
• Noise Parameters
– Signal to noise ratio
– Noise factor
– Noise equivalent band width
– Effective noise temperature
P. Suresh Venugopal
Analog Communication - NOISE
3
Topics to be covered
• Narrow band noise
– Representation of narrowband noise in terms of In
phase and Quadrature Components
• Noise in CW modulation Systems
– Noise in linear Receivers using Coherent detection
– Noise in AM Receivers using Envelope detection
– Noise in FM Receivers
P. Suresh Venugopal
Analog Communication - NOISE
4
Noise Sources
• Introduction to Noise
• Shot Noise
• Thermal Noise
• Flicker Noise
• White Noise
P. Suresh Venugopal
Analog Communication - NOISE
5
Noise - Introduction
• Noise – Unwanted Signals that tend to disturb the
Transmission and Processing of Signals in
Communication System and over which we have
incomplete control.
• Noise is a general term which is used to describe
an unwanted signal which affects a wanted signal.
• These unwanted signals arise from a variety of
sources.
P. Suresh Venugopal
Analog Communication - NOISE
6
Sources of Noise
• Sources of noise may be:
– External
– Internal
• Naturally occurring external noise sources include:
– Atmosphere disturbance (e.g. electric storms, lighting,
ionospheric effect etc), so called ‘Sky Noise’
– Cosmic noise which includes noise from galaxy, solar
noise
– ‘Hot spot’ due to oxygen and water vapour resonance
in the earth’s atmosphere.
P. Suresh Venugopal
Analog Communication - NOISE
7
Sources of Noise
• Noise performance by external sources is shown
below.
Sources of Noise
• Internal Noise is an important type of noise that
arises from the SPONTANEOUS FLUCTUATIONS of
Current or Voltage in Electrical Circuits.
• This type of noise is the basic limiting factor of
employing more complex Electrical Circuits in
Communication System.
• Most Common Internal Noises are:
– Shot Noise
– Thermal Noise
P. Suresh Venugopal
Analog Communication - NOISE
9
Shot Noise
• Shot Noise arises in Electronic Components like
Diodes and Transistors.
• Due to the discrete nature of Current flow In
these components.
• Take an example of Photodiode circuit.
• Photodiode emits electrons from the cathode
when light falls on it.
• The circuit generates a current pulse when an
electron is emitted.
P. Suresh Venugopal
Analog Communication - NOISE
10
Shot Noise
• The electrons are emitted at Random times, Ʈk
where -∞ < k < ∞ and assume this random
emission have been gone for a long time.
• Thus the Total Current flowing through the
Photodiode may be modeled as the sum of these
Current Pulses.
• This process X(t) is Stationary and is called SHOT
NOISE
P. Suresh Venugopal
Analog Communication - NOISE
11
Thermal Noise
• Thermal Noise is the name given to the Electrical Noise arising
from the Random motion of electrons n a conductor.
• It is also called Jonson Noise or Nyquist Noise.
• Let VTN is the Thermal Noise Voltage appearing across the two
terminals of a resistor.
• Let the applied voltage have a bandwidth or frequency), ∆f.
• Then the Mean Square value of VTN is given by:
P. Suresh Venugopal
Analog Communication - NOISE
12
Thermal Noise
• Where
k = Boltzmann’s constant = 1.38 x 10-23 Joules per oK
T = absolute temperature in oK
R = resistance in ohms
P. Suresh Venugopal
Analog Communication - NOISE
13
Jonson Noise or Nyquist Noise
P. Suresh Venugopal
Analog Communication - NOISE
14
Thermal Noise
• We can model a noisy resistor using the Thevenin and
Norton Equivalent Circuit as shown below:
Thermal Noise
• The number of electrons inside a resistor is very
large and their random motions inside the
resistors are statistically independent.
• The Central Limiting Theorem indicates that
thermal Noise is a Gaussian Distribution with Zero
mean.
P. Suresh Venugopal
Analog Communication - NOISE
16
Low Frequency or Flicker Noise
• Active devices, integrated circuit, diodes, transistors etc also
exhibits a low frequency noise, which is frequency
dependent (i.e. non uniform) known as flicker noise .
• It is also called ‘one – over – f’ noise or 1/f noise because of
its low-frequency variation.
• Its origin is believed to be attributable to contaminants and
defects in the crystal structure in semiconductors, and in
the oxide coating on the cathode of vacuum tube devices
P. Suresh Venugopal
Analog Communication - NOISE
17
Low Frequency or Flicker Noise
• Flicker Noise is found in many natural phenomena such as
nuclear radiation, electron flow through a conductor, or
even in the environment.
• The noise power is proportional to the bias current, and,
unlike Thermal and Shot Noise, Flicker Noise decreases with
frequency.
• An exact mathematical model does not exist for flicker
noise because it is so device-specific.
• However, the inverse proportionality with frequency is
almost exactly 1/f for low frequencies, whereas for
frequencies above a few kilohertz, the noise power is weak
but essentially flat.
P. Suresh Venugopal
Analog Communication - NOISE
18
Low Frequency or Flicker Noise
• Flicker Noise is essentially random, but because its frequency
spectrum is not flat, it is not a white noise.
• It is often referred to as pink noise because most of the power is
concentrated at the lower end of the frequency spectrum.
• Flicker Noise is more prominent in FETs (smaller the channel length,
greater the Flicker Noise), and in bulky carbon resistors.
• The objection to carbon resistors mentioned earlier for critical low
noise applications is due to their tendency to produce flicker noise
when carrying a direct current.
• In this connection, metal film resistors are a better choice for low
frequency, low noise applications.
P. Suresh Venugopal
Analog Communication - NOISE
19
White Noise
• The Noise Analysis of Communication System is
done on the basis of an idealized form of noise
called WHITE NOISE.
• Its power spectral density is independent on
operating frequency.
• White – White light contain equal amount of all
frequencies in visible spectrum.
P. Suresh Venugopal
Analog Communication - NOISE
20
White Noise
• Power spectral density is given by:
The 1/2 here emphasizes that the
spectrum extends to both positive
and negative frequencies.
P. Suresh Venugopal
Analog Communication - NOISE
21
Power Spectral Density of White
Noise
• A random process W(t) is called white noise if it
has a flat power spectral density, i.e., SW(f) is a
constant c for all f.
P. Suresh Venugopal
Analog Communication - NOISE
22
Ideal Low Pass Filtered White
Noise
• Let
– w(t) = White Gaussian Noise applied to the LPF
– B = Bandwidth of LPF
– n(t) = noise appearing at the output of LPF
– SN(f) = Power Spectral Density of n(t)
– RN(Ʈ) = Auto Correlation function of n(t)
P. Suresh Venugopal
Analog Communication - NOISE
23
Ideal Low Pass filtered White
Noise
P. Suresh Venugopal
Analog Communication - NOISE
24
Noise Parameters
• Signal to noise ratio
• Noise factor
• Noise equivalent band width
• Effective noise temperature
P. Suresh Venugopal
Analog Communication - NOISE
25
Signal to Noise Ratio (SNR)
SNR dB   10 log 10
where:
 PS

 PN



PS is the signal power in watts
PN is the noise power in watts
• Hartley-Shannon Theorem (also called Shannon’s Limit)
states that the maximum data rate for a communications
channel is determined by a channel’s bandwidth and SNR.
• A SNR of zero dB means that noise power equals the
signal power.
P. Suresh Venugopal
Analog Communication - NOISE
26
Noise Figure / Factor (NF or F or Fn)
• Electrical noise is defined as electrical energy of
random amplitude, phase, and frequency.
• It is present in the output of every radio receiver.
• The noise is generated primarily within the input
stages of the receiver system itself.
• Noise generated at the input and amplified by the
receiver's full gain greatly exceeds the noise
generated further along the receiver chain.
P. Suresh Venugopal
Analog Communication - NOISE
27
Noise Figure / Factor (NF or F or Fn)
• The noise performance of a receiver is described
by a figure of merit called the noise figure (NF).
• where G = Antenna Gain
P. Suresh Venugopal
Analog Communication - NOISE
28
Noise equivalent band width
P. Suresh Venugopal
Analog Communication - NOISE
29
Effective noise temperature
•
•
•
•
N
T
KB
T = environmental temperature (Kelvin)
N = noise power (watts)
K = Boltzmann’s constant (1.38 10 -23 J/K)
B = total noise factor (hertz)
Te  T  F 1
• Te = equivalent noise temperature
• F = noise factor (unitless)
P. Suresh Venugopal
Te
F  1
T
Analog Communication - NOISE
30
Narrowband
Noise
• Introduction to Narrowband Noise
• Representation of narrowband noise in terms of
In phase and Quadrature Components
P. Suresh Venugopal
Analog Communication - NOISE
31
Narrow band noise
• Preprocessing of received signals
• Preprocessing done by a Narrowband Filter
• Narrowband Filter – Bandwidth large enough to
pass the modulated signal.
• Noise also pass through this filter.
• The noise appearing at the output of this NB filter
is called NARROWBAND NOISE.
P. Suresh Venugopal
Analog Communication - NOISE
32
Narrow band noise
• Fig (a) – spectral components of NB Noise concentrates about +fc
• Fig (b) – shows that a sample function n(t) of such process appears
somewhat similar to a sinusoidal wave of frequency fc
Narrow band noise
• We need a mathematical representation to analyze the
effect of this NB Noise.
• There are 2 specific representation of NB Noise
(depending on the application)
P. Suresh Venugopal
Analog Communication - NOISE
34
Representation of narrowband noise in
terms of In phase and Quadrature
Components
• Let n(t) is the Narrowband Noise with Bandwidth
2B centered at fc
• We can represent n(t) in canonical (standard) form
as:
• We can extract nI(t) (In Phase Component) and
nQ(t) (Quadrature Component) from n(t).
P. Suresh Venugopal
Analog Communication - NOISE
35
Extraction of nI(t) and nQ(t) from
n(t)
• Each LPF have bandwidth ‘B’
• This is known as NARROWBAND NOISE ANALYSER
Generation of n(t) from nI(t) and
nQ(t)
• This is known as NARROWBAND NOISE SYNTHESISER
P. Suresh Venugopal
Analog Communication - NOISE
37
Important properties of nI(t) and
nQ(t)
Important properties of nI(t) and
nQ(t)
P. Suresh Venugopal
Analog Communication - NOISE
39
Noise in CW modulation
Systems
• Noise in linear Receivers using Coherent detection
• Noise in AM Receivers using Envelope detection
• Noise in FM Receivers
P. Suresh Venugopal
Analog Communication - NOISE
40
Gaussian process
• Let X(t) denote a random process for an interval that starts at
time t = 0 and lasts until t = T.
• The random variable Y is a linear functional of the random
process X(t) if:
where g(t) is an arbitrary function
• By definition:
The random process X(t) is a Gaussian process if every linear
functional of X(t) is a Gaussian random variable.
P. Suresh Venugopal
Analog Communication - NOISE
41
Main virtues of the Gaussian process:
• Gaussian process has many properties that make results
possible in analytic form
• Random processes produced by physical phenomena (see
thermal noise as an example) are often such that they
may be modeled by the Gaussian process
• If the input to a linear time invariant (LTI) system is
Gaussian then its output is also Gaussian
P. Suresh Venugopal
Analog Communication - NOISE
42
Thermal noise
• Is generated by each resistor.
• Used to model channel noise in analysis the of
communication systems.
• It is an ergodic, Gaussian process with the
mean of zero.
P. Suresh Venugopal
Analog Communication - NOISE
43
Gaussian distribution
• Main virtue of the Gaussian process:
Two parameters, the mean and variance are enough
to fully characterize a Gaussian distribution.
P. Suresh Venugopal
Analog Communication - NOISE
44
Power spectral density (PSD) of a
random process
• By definition, the power spectral density SX(t) and autocorrelation
function RX(Ʈ) of an ergodic random process X(t) form a Fourier
transform pair with Ʈ and f as the variables of interest.
• The power of an ergodic random process X(t) is equal to the total
area under the graph of power spectral density.
• The power spectral density is that characteristic of a random
process which is easy to measure and which is used in
communication engineering to characterize noise.
45
White Gaussian Noise
• Gaussian means Gaussian process.
A measurable consequence: Measured instantaneous values of a
thermal noise give a Gaussian distribution.
• White means that the autocorrelation function consists of a delta
function weighted by the factor N0=2 and occurring a Ʈ = 0.
• Power spectral density of white noise is:
P. Suresh Venugopal
Analog Communication - NOISE
46
White Gaussian Noise
P. Suresh Venugopal
Analog Communication - NOISE
47
White Gaussian Noise
• Thermal noise is a white Gaussian noise.
• It is an ergodic Gaussian process with mean of zero, its power is
given by the variance σ2.
• Its power spectral density is:
where k is the Boltzmann’s constant and Te is the equivalent noise
temperature.
• Note:
Power of white noise is infinite. Only the bandlimited white
noise has a finite power!
P. Suresh Venugopal
Analog Communication - NOISE
48
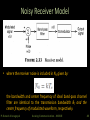
Noisy Receiver Model
• where the receiver noise is included in N0 given by:
the bandwidth and center frequency of ideal band-pass channel
filter are identical to the transmission bandwidth BT and the
center frequency of modulated waveform, respectively.
P. Suresh Venugopal
Analog Communication - NOISE
49
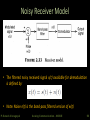
Noisy Receiver Model
• The filtered noisy received signal x(t) available for demodulation
is defined by:
• Note: Noise n(t) is the band-pass filtered version of w(t)
P. Suresh Venugopal
Analog Communication - NOISE
50
Power spectral density (PSD) of bandpass filtered noise
• The average noise power may be calculated from the power spectral
density.
• The average power N of filtered Gaussian white noise is:
P. Suresh Venugopal
Analog Communication - NOISE
51
Signal to Noise Ratio (SNR)
• A measure of the degree to which a signal is
contaminated with additive noise is the signalto-noise ratio (SNR)
P. Suresh Venugopal
Analog Communication - NOISE
52
Figure of Merit Of CW Modulation
Schemes
• Goal: Compare the performance of different CW modulation
schemes.
• Signal-to-noise ratio (SNR) is a measure of the degree to which a
signal is contaminated by noise.
• Assume that the only source of degradation in message signal
quality is the additive noise w(t).
• Noisy receiver model:
53
Figure of Merit Of CW Modulation
Schemes
• The signal-to-noise ratio at the demodulator input:
• The signal-to-noise ratio at the demodulator output:
P. Suresh Venugopal
Analog Communication - NOISE
54
Figure of Merit Of CW Modulation
Schemes
• (SNR)O is well defined only if the recovered message signal
and noise appear additively at demodulator output. This
condition is:
– Always valid for coherent demodulators
– But is valid for noncoherent demodulators only if the input signal
to- noise ratio (SNR)I is high enough
• Output signal-to-noise ratio (SNR)O depends on:
– Modulation scheme
– Type of demodulator
P. Suresh Venugopal
Analog Communication - NOISE
55
Figure of Merit Of CW Modulation
Schemes
Conditions of comparison
• To get a fair comparison of CW modulation schemes and receiver
configurations, it must be made on an equal basis.
– Modulated signal s(t) transmitted by each modulation scheme has the same
average power
– Channel and receiver noise w(t) has the same average power measured in the
message bandwidth W
• According to the equal basis, the channel signal-to-noise ratio is
defined as:
56
Figure of Merit Of CW Modulation
Schemes
• Noise performance of a given CW modulation scheme and a given
type of demodulator is characterized by the figure of merit.
• By definition, the figure of merit is:
• The higher the value of the figure of merit, the better the noise
performance
P. Suresh Venugopal
Analog Communication - NOISE
57
SNRs & Figure of Merit
P. Suresh Venugopal
Analog Communication - NOISE
58
Noise in AM DSB-FC Receivers
- AM signal
s(t)  A C [1  k a m(t)]cos(2 πf C t)
- Average signal power  A C2 (1  k a2 P) 2
- Average noise power  WN 0 ← (2W 
(SNR) C, AM
N0
)
2
A C2 (1  k a2 P)

2WN 0
- Filtered signal
x(t)  s(t)  n(t)
 [A C  A C k a m(t)  n I (t)]cos(2 πf C t) - n Q (t)sin(2 πf C t)
59
Noise in AM DSB-FC Receivers
y (t )  envelop of x(t)

 [A C  A C k a m(t)  n I (t)]  n (t)
2
2
Q

1
2
Assume A C [1  k a m(t)]  n I (t), n Q (t)
y(t)  A C  A C k a m(t)  n I (t)
- (SNR) O,AM
A C2 k a2 P

2WN 0
Avg carrier power  Avg noise power

 ka ≤ 1
Figure of merit
P. Suresh Venugopal
( SNR) O
( SNR) C
AM
k a2 P

1
2
1 kaP
Analog Communication - NOISE
60
Threshold effect
• The threshold is a value of carrier-to-noise ratio below
which the noise performance of a demodulator
deteriorates much more rapidly than proportionately to
the carrier-to-noise ratio.
• Every noncoherent detector exhibits a threshold effect,
below the threshold the restored message signal
becomes practically useless.
P. Suresh Venugopal
Analog Communication - NOISE
61
Noise in AM DSB-FC Receivers
• Figure of merit for DSB modulation:
where P denotes the average power of message signal m(t)
and ka is the amplitude sensitivity of AM modulator.
• The best figure of merit is achieved if the modulation factor is
µ = kaAm = 1
• DSB system using envelope detection must transmit three
times as much average power as a suppressed-carrier system
P. Suresh Venugopal
Analog Communication - NOISE
62
Threshold effect
Physical explanation:
• If the carrier-to-noise ratio is high enough then the signal
dominates and the noise causes only a small unwanted
AM and PM.
• However, if the carrier-to-noise ratio is small then the
noise dominates which results in a complete loss of
information.
• As a result, the demodulator output does not contain the
message signal at all.
P. Suresh Venugopal
Analog Communication - NOISE
63
Threshold effect
Threshold Effect : loss of message in an envelope detector that
operates at a low CNR.
64
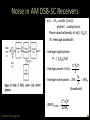
Noise in AM DSB-SC Receivers
P. Suresh Venugopal
Analog Communication - NOISE
65
Noise in AM DSB-SC Receivers
- s( t )  CA C cos( 2π fC t )m( t )
where C : scaling factor
Power spectral density of m(t) : SM (f)
W : message bandwidth
- Average signal power
P  ∫ -WW SM (f) df
C2 A C2 P
- Average power of s(t) 
2
N
- Average noise power  2W  0  W N0
2
(baseband)
- (SNR )C,DSB
P. Suresh Venugopal
C2 A C2 P

2W N0
66
Noise in AM DSB-SC Receivers
Finding (SNR)O
- x( t )  s( t )  n( t )
 CA C cos( 2π fC t )m( t )  nI ( t ) cos( 2π fC t )  nQ ( t ) sin( 2π fC t )
- v( t )  x( t ) cos( 2π fC t )
1
1
1
1
 CA Cm( t )  nI ( t )  CA Cm( t )  nI ( t )cos( 4π fC t )  A CnQ ( t ) sin( 4π fC t )
2
2
2
2
∴ y(t) 
1
1
CA Cm( t )  nI ( t )
2
2
P. Suresh Venugopal
Analog Communication - NOISE
67
Noise in AM DSB-SC Receivers
Finding (SNR)O
2
C2 A C
P
- Average signal power 
4
1
1
- Average noise power  (2W)N0  W N0 (passband)
4
2
 Power(nI (t))  Power of band pass filtered noise n(t)  2W N0
2
2
C2 A C
P 4 C2 A C
P
- ∴ (SNR)O 

W N0 2
2W N0
∴ Figure of merit
P. Suresh Venugopal
(SNR)O
(SNR)C
1
DSB  SC
Analog Communication - NOISE
68
Noise performance of AM receivers
Note: For high value of (SNR)C, the noise performance of coherent and
noncoherent DSB are identical. But noncoherent DSB has a
threshold effect. Coherent AM detectors have no threshold effect!
P. Suresh Venugopal
Analog Communication - NOISE
69
Comparison of noise performance of
AM modulation schemes
Remarks
• Curve I: DSB modulation
and envelope detector
with modulation factor
µ=1
• Curve II: DSB–SC and
SSB with coherent
demodulator
• Note the threshold
effect that appears at
about 10 dB
P. Suresh Venugopal
Analog Communication - NOISE
70
Noise in FM Receivers
• w(t): zero mean white Gaussian noise with PSD = No/2
• s(t): carrier = fc,
BW = BT
• BPF: [fC - BT/2 - fC + BT/2]
• Amplitude limiter: remove amplitude variation.
• Discriminator
» Slope network : varies linearly with frequency
» Envelope detector
P. Suresh Venugopal
Analog Communication - NOISE
71
Noise in FM Receivers
• FM signal: s( t )  A C cos[2π fC t  2π k f ∫ 0t m( t )dt ]
φ( t )  2π k f ∫ 0t m( t )dt
s( t )  A C cos[ 2π fC t  φ( t )]
• Filtered noise n(t):
n( t )  nI ( t ) cos( 2π fC t )  nQ ( t ) sin( 2π fC t )
 r(t)cos[2π fC t  ψ( t )]
P. Suresh Venugopal
r(t)  (n ( t ))2  (n ( t ))2
I
Q

where 
1  n Q ( t ) 
ψ
(
t
)

tan

 n (t) 
 I 

Analog Communication - NOISE
72
Noise in FM Receivers
• Phasor diagram interpretation of noisy demodulator input:
• Due to the PM generated by the noise, noise appears at the
demodulator output.
• But the FM demodulator is sensitive to the instantaneous
frequency of the input signal.
• The instantaneous frequency is the first derivative of the
phase of input signal.
P. Suresh Venugopal
Analog Communication - NOISE
73
Noise in FM Receivers
• The instantaneous frequency is the first derivative of the
phase of input signal.
• Derivation in the time domain corresponds to multiplication by
(j2πf) in the frequency domain.
• Multiplication by (j2πf) means that the frequency response of
derivation is:
• Recall, power spectral density of the output process equals to
the PSD of the input process multiplied by the squared
magnitude of the frequency response H(f) of the LTI two-port.
P. Suresh Venugopal
Analog Communication - NOISE
74
Noise in FM Receivers
• Recall, power spectral density of the output process equals to
the PSD of the input process multiplied by the squared
magnitude of the frequency response H(f) of the LTI two-port.
• Therefore, the PSD SN0(f) of noise at an FM receiver output has
a square-law dependence on the operating frequency.
• The high-frequency noise is dominant at the output of an FM
receiver
P. Suresh Venugopal
Analog Communication - NOISE
75
Noise in FM Receivers
Discriminator output
1 dθ(t)
v( t ) 
 k f m( t )  nd ( t )
2π dt
where
1 d
nd ( t ) 
{r( t ) sin[ψ( t )  φ( t )]}
2πA C dt
1 d

{r( t ) sin[ψ( t )]}
2πA C dt
1 dnQ ( t )
 nd ( t ) 
2πA C dt
P. Suresh Venugopal
Analog Communication - NOISE
76
Noise in FM Receivers
P. Suresh Venugopal
Analog Communication - NOISE
77
Noise in FM Receivers
P. Suresh Venugopal
Analog Communication - NOISE
78
Noise in FM Receivers
P. Suresh Venugopal
Analog Communication - NOISE
79
Noise in FM Receivers
P. Suresh Venugopal
Analog Communication - NOISE
80
Noise in FM Receivers
Figure of merit for frequency modulation
• If the (SNR)C is high enough and exceeds the threshold level
then:
• where P denotes the average power of message signal m(t), kf
is the frequency sensitivity of FM modulator and W denotes
the bandwidth of message signal.
• Since:
• and for wide-band FM we may write:
P. Suresh Venugopal
Analog Communication - NOISE
81
Noise in FM Receivers
Figure of merit for frequency modulation
• we obtain by substituting:
where β is the Modulation Index.
• Note: An increase in the transmission bandwidth BT provides a
corresponding quadratic increase in the output signal-to-noise ratio
(or in the figure of merit) of the FM system.
P. Suresh Venugopal
Analog Communication - NOISE
82
FM threshold effect
• The figure of merit discussed above is valid only if the
carrier-to-noise ratio (SNR)C is high compared with unity.
• It has been found experimentally that as (SNR)C is
decreased below a threshold, each FM demodulator,
either coherent or noncoherent, breaks:
– At first isolated clicks are heard and if the (SNR)C is decreased
further, the clicks rapidly merge into a crackling. sound
P. Suresh Venugopal
Analog Communication - NOISE
83
FM threshold effect
A qualitative explanation
• If (SNR)C is small then the noise becomes dominant and the
phasor representation and the decomposition of noise into a
PM and AM are not valid any more.
• The phase of noise is a random variable and it may take any
value.
• Recall, the FM demodulator is sensitive to the derivate of
phase.
• When the phase of demodulator input varies suddenly by 2π
due to the noise then an impulse, i.e., click appears at the
receiver output.
P. Suresh Venugopal
Analog Communication - NOISE
84
Pre-emphasis and de-emphasis in FM
systems
• Recall: The power spectral density SN0(f) of noise at an FM receiver
output has a square law dependence on the operating frequency.
• The high-frequency noise is dominant at the output of an FM
receiver.
• The power spectral density of
message signals usually falls
off at higher frequencies.
• Generally, the most part of a
message signal is in the lowfrequency region.
• These facts may be exploited
to
improve
the
noise
performance of FM systems
P. Suresh Venugopal
Analog Communication - NOISE
85
Pre-emphasis and de-emphasis in FM
systems
• Basic idea
– Apply a filter at the demodulator output which reduces the high
frequency content of the output spectrum.
– To compensate this attenuation, a pre-emphasis must be
applied to the high-frequency signals at the transmitter
• Pre-emphasis at the transmitter:
– A filter that artificially emphasize the high-frequency
components of the message signal prior to the modulation.
P. Suresh Venugopal
Analog Communication - NOISE
86
Pre-emphasis and de-emphasis in FM
systems
• De-emphasis at the receiver:
– An inverse operation performed by a filter placed after the
demodulation.
– The de-emphasis filter restores the original signal by deemphasizing the high-frequency components.
• Effects of pre-emphasis and de-emphasis filters cancel each other:
P. Suresh Venugopal
Analog Communication - NOISE
87
Use of pre-emphasis and de-emphasis
in an FM system
P. Suresh Venugopal
Analog Communication - NOISE
88
Comparison of noise performance of
CW systems
• Note: Threshold problem is more serious in FM modulation than in
AM. The higher the β, the better the FM noise performance. But the
price to be paid is the wider transmission bandwidth
P. Suresh Venugopal
Analog Communication - NOISE
89