Download Modelling infectious diseases - Faculty of Medicine

Modelling infectious
diseases
Jean-François Boivin
25 October 2010
1
2
3
This decline prompted the
U.S. Surgeon General to
declare in 1967 that "the
time has come to close the
book on infectious
diseases."
4
5
Dear Sir: In your excellent Science paper
(28 January 2000), you quote the US
Surgeon General ('the time has come to
close the book on infectious diseases').
You did not provide a reference for that
quote, and I would like very much to know
exactly where it comes from for a lecture I
am preparing on infectious diseases. Can
you help identify this reference? Thank
you very much.
Jean-François Boivin, MD, ScD
Professor
Faculty of Medicine
McGill University
Montreal
Canada
6
7
I regret that Bob May has been over generous
in its attribution. The only reference I have is
that the statement was made in 1967 but I
have no formal source.
Best wishes.
George Poste
8
Two objectives:
• Understanding population
dynamics of the transmission of
infectious agents
• Understanding potential impact
of interventions
9
Rothman, Greenland (1998)
10
Chickenpox
Epidemic spread due to children who do not appear to be sick
11
14 days
Day 10
Parasite becomes
infectious for
mosquitoes
Malaria (Plasmodium falciparum)
early treatment may affect transmission
12
A public health nightmare: HIV
days
weeks
median > 10 years
13
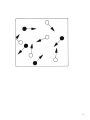
SiR model
S
R
i
3 population densities (persons per mile2)
X
+
Y
+
Z
= N
Reference: Chapter 6 in: Nelson et al. (2001)
14
Process begins here with 1
infectious subject
Infectious subject enters in
contact with susceptible
and then the movement of
subjects begins
S

i

R
Assumptions
Direct transmission
Life-long immunity
(prototype: measles)
Population is closed (no entry, no exit)
15
Nelson (2001)
βXY = incidence of infection (modelling assumptions)
γY = incidence of removals (cured, immune, dead)
direct observations from clinical epidemiology
16
Oxford Textbook of Public Health. Volume 2. Second edition. 1991
17
18
Imagine susceptible and infectious
individuals behaving as ideal gas
particles within a closed system
X = number of particles of one gas
(susceptibles)
Y = number of particles of a second
gas (infectious people)
β = collision coefficient for the
formation of molecules of a new
gas from one molecule each of the
original gases (i.e. new cases of
infection)
19
Gas particles (individuals) are
mixing in a homogeneous manner
such that collisions (contacts) occur
at random. The law of mass action
states that the net rate of
production of new molecules (i.e.
cases), I, is:
I = βXY
20
The coefficient β is a measure of
(i) the rate at which collisions
(contacts) occur
(ii) the probability that the repellent
forces of the gas particles can be
overcome to produce new
molecules,
or, in the case of infection, the
likelihood that a contact between a
susceptible and an infectious person
results in the transmission of infection
21
X:
number of black molecules
Y:
number of white molecules
β:
rate of collisions and probability that collision will
lead to creation of a new molecule
22
Under these assumptions, the
incidence of infection will be
increased by
larger numbers of infectious and
susceptible persons
and/or high probabilities (β) of
transmission
23
Example 1
Area = 1 mile2
S = 8,699 persons
i = 1 person
R = 0 person
Area of movement = 0.001 mile2 per person per day
• random movement
• homogeneous
distribution of
subjects
Probability of infection per contact = 40% data?
Average duration of a case = 2 days
Incidence of recoveries = 0.5 case/day
Initial rate of infection :
(area of movement) (probability of infection) (i x S) =
0.001 mile2
person·day
x 0.4 x 1 person x 8,699 persons = 3.48 cases
mile2
mile2
day·mile2
Infection rate > recovery rate; infection will spread
The initial case lasted 2 days, generating 3.48 x 2 = 6.96 secondary cases
= basic reproductive rate
24
(Nelson 2001)
25
Example 2
Area = 1 mile2
S = 1,249 persons
i = 1 person
R = 0 person
Area of movement = 0.001 mile2 per person per day
Probability of infection per contact = 40%
Average duration of a case = 2 days
Incidence of recoveries = 0.5 case/day
Initial rate of infection :
(area of movement) (probability of infection) (i x S) =
0.001 mile2 x 0.4 x 1 person x 1,249 persons = 0.5 cases
person·day
mile2
mile2
day·mile2
Infection rate = recovery rate
Infection will not spread
The initial case lasted 2 days, generating 0.5 x 2 = 1 secondary case
26
Basic reproduction ratio
= basic reproductive rate (R of R0)
= the number of secondary cases generated from a single
infective case introduced into a susceptible population
= (initial infection rate) x (duration of infection)
or :
Rate of infection
Rate of recovery
27
(Nelson 2001)
28
29
Although the population biology of
measles depends on many factors,
such as seasonality of transmission
and the social, spatial, and age
structure of the population, the fate
of an epidemic can be predicted by a
single parameter: the reproductive
number R, defined as the mean
number of secondary infections per
infection
30
If the reproductive number is smaller
than one, the disease will not persist but
will manifest itself in outbreaks of
varying size triggered by importations of
the disease.
31
If the reproductive number approaches
one, large outbreaks become increasingly
likely, and, if it exceeds one, the disease
can become endemic.
32
If the reproductive number equals one,
the situation is said to be at criticality.
33
A decline in vaccine uptake will lead to
increasingly large outbreaks of measles
and, finally, the reappearance of measles
as an endemic disease.
34
The effect of mass immunization is to reduce
the basic reproduction ratio ...
Defining R’ to be the basic reproduction ratio
after immunization and v to be the proportion
vaccinated and effectively immunized,
R’ = R(1 – v)
(Nelson 2001, page 161)
35
NEJM 2003; 349: 2431-2441
36
Science 2003; 300: 1966-1970
37
38
39
Nelson KE, William CM, Graham
NMH. Infectious disease
epidemiology. Theory and practice.
Aspen Publishers. Gaithersburg,
Maryland. 2001
40