Download Why napkin math may not add up: Arithmetic and geometric means

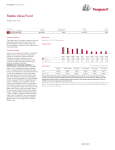
Research note
Why napkin math may not add up:
Arithmetic and geometric means
Vanguard research
Authors
Jill Marshall
Anatoly Shtekhman, CFA
March 2011
Many times investment managers attempt to
estimate portfolio return expectations by
jotting down the asset weightings and
multiplying them by the appropriate
expected returns. Pretty simple, but maybe
not accurate. This “cocktail napkin” math
often misses the mark, especially for asset
classes with high volatility or rebalanced
portfolios. An understanding of arithmetic
and geometric averages can help.
If we define volatility as the square of the
standard deviation, then the formula to calculate
the geometric mean is GM = AM – 0.5 ×
volatility.1 The higher the volatility, the greater
the difference between the means. As a result,
there is greater disparity between the AM and
GM for equities than for fixed income during the
1930–2010 period.
Figure 1.
The arithmetic mean (AM), commonly known
as an average, is a different calculation than
the geometric mean (GM), which has utility in
finance and science. Too often AM and GM are
used interchangeably. Here are two examples
showing why that can lead to error.
What was the average return for equities
from 1930 through 2010?
(a) 11.4%
(b) 9.2%
(c) Both
1930–2010
AM
Stocks
AM
Bonds
GM
Stocks
GM
Bonds
11.4%
5.8%
9.4%
5.6%
What was the average return for a 60%
equity/40% fixed income portfolio from 1930
through 2010?
(a) 9.1%
If you answered (c), you are right: 11.4% is the
arithmetic mean and 9.2% is the geometric
mean. Both are mathematically correct, but the
difference between them has implications for
investors seeking to project returns based on
history. The reason the arithmetic and
geometric averages are different is volatility.
Arithmetic and geometric means for
U.S. stocks and bonds, 1930–2010
(b) 8.3%
(c) Both
Again, the answer is (c): 9.1% is the AM and
8.3% is the GM. For a portfolio with more
than one asset class, there are two reasons
for the difference between the means. One is
the volatility of the portfolio, as discussed
above, and the other is the effect of
1 Substituting the actual numbers in the equation: 11.4% – (0.5 × 3.7%) = 9.5%. The GMs are slightly different because equities are not
normally distributed.
Connect with Vanguard > vanguard.com
rebalancing over time; both affect the GM.
Regular adjustments to bring the portfolio back to a
60%/40% split automatically influence the average
return calculations.
Furthermore, if the geometric means for the two
asset classes are calculated separately, the
combined result will be less than the actual
geometric mean for the 60%/40% portfolio.2
Summary
There is no napkin-math shortcut to accurately
estimating portfolio return. When measuring
cumulative averages over time, it is critical to
understand which average you care about and
calculate accordingly. The fact is that the best way to
estimate portfolio returns is to calculate directly from
the time series.
Note: All investments are subject to risk. Past performance is no guarantee of future returns.
2 Returns reported in Vanguard’s Economic and Capital Markets Outlook are geometric returns.
Connect with Vanguard® > vanguard.com
Vanguard research >
Vanguard Center for Retirement Research
Vanguard Investment Counseling & Research
Vanguard Investment Strategy Group
P.O. Box 2600
Valley Forge, PA 19482-2600
E-mail > [email protected]
CFA® is a trademark owned by CFA Institute.
© 2011 The Vanguard Group, Inc.
All rights reserved.
Vanguard Marketing Corporation, Distributor.
ICRWNM 032011