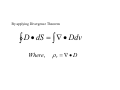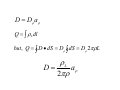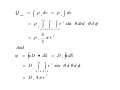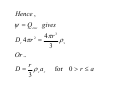* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download ELECTRIC FIELD ELECTRIC FLUX GAUSS LAW
Survey
Document related concepts
Transcript
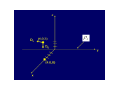
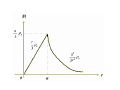
ELECTRIC FIELD ELECTRIC FLUX GAUSS LAW Today….. • More on Electric Field: – Continuous Charge Distributions • Electric Flux: – Definition – How to think about flux Summary Electric Field Lines Electric Field Patterns Dipole Point Charge Infinite Line of Charge Two types of electric charge: opposite charges attract, like charges repel 1 Q1Q2 ∧ F12 = 2 r12 4πε 0 r12 → Coulomb’s Law: Electric Fields → Charges respond to electric fields: Charges produce electric fields: → F = qE q E=k 2 r Electric Flux Flux: Let’s quantify previous discussion about field-line “counting” Define: electric flux ψ through the closed surface S ψ = ∫ E • dS S “S” is surface of the box Electric Flux ψ = ∫ E • dS S •What does this new quantity mean? • The integral is over a CLOSED SURFACE → → • Since E • dS is a SCALAR product, the electric flux is a SCALAR quantity → • The integration vector dS is normal to the surface and points OUT → → of the surface. E • dS is interpreted as the component of E which is NORMAL to the SURFACE. • Therefore, the electric flux through a closed surface is the sum of the normal components of the electric field all over the surface. • The sign matters!! Pay attention to the direction of the normal component as it penetrates the surface… is it “out of” or “into” the surface? • “Out of” is “+” “into” is “-” How to think about flux • We will be interested in net flux in or out of a closed surface like this box • This is the sum of the flux through each side of the box – consider each side separately • Let E-field point in y-direction → – then E and → → → S are parallel and → E • S = E w2 ELECTRIC FLUX DENSITY We define electric flux ψ D = ε0E in terms of D ψ = ∫ D • dS For example, for an infinite sheet of charge ρs E= an , 2ε 0 ⎛ ρs ⎞ ρs ⎟⎟ a n = D = ε 0 ⎜⎜ an 2 ⎝ 2ε 0 ⎠ For line charge distribution ρL ρL E= aρ , D = aρ 2πε 0 ρ 2πρ For volume charge distribution ρV dv ρV dv E=∫ a D = a , R ∫ 2 2 R 4πε 0 R 4πR Example: Determine D at (4,0,3) if there is a point charge -5π mC at (4,0,0) and a line charge 3 π mC/m along the y axis. Let D = DQ + DL where DQ and DL are flux densities due to the point charge and line charge respectively. Q Q(r − r ) DQ = ε 0 E = aR = 2 ' 3 4πR 4π r − r ' Where r – r’ =(4,0,3) –(4,0,0)=(0,0,3).Hence, − 5π x 10 − 3 (0,0,3 ) mC 2 DQ = = − 0 . 138 a 3 z m 4π 0,0,3 Also, ρL DL = aρ 2πρ aρ ( (4,0,3) − (0,0,0) ) (4,0,3) = = (4,0,3) − (0,0,0) 5 3π (4ax + 3az ) = 0.24ax + 0.18az mC m 2 DL = 2π (5)(5) Thus, D = DQ + DL C µ D = 240 a x + 42 a z m2 GAUSS’S LAW-MAXWELL’S EQUATION Gauss’s Law states that the total electric flux ψ through any closed surface is equal to the total charge, Q enclosed by that surface . ψ = Qenc That is ψ = ∫ dψ = ∫ D • dS S = Total Charge enclosed , where Q = ∫ ρ v dv v ∴ Q = ∫ D • dS = ∫ ρ v dv S v The integration is performed over a closed surface, i.e. gaussian surface. By applying Divergence Theorem ∫ D • dS = ∫ ∇ • Ddv Where, ρV = ∇ • D APPLICATION OF GAUSS’S LAW A. Point Charge Since D is everywhere normal to gaussian surface, that is D = Dr ar From Gauss Law, ψ = Qenc Q = ∫ D • dS = Dr ∫ dS = Dr 4πr Where ∫ D • dS = 2π ∫φ θ π 2 2 2 r sin θ d θ d φ = 4 π r ∫ =0 =0 Q ∴D = ar 2 4π r B. Infinite Line of Charge Suppose the infinite of uniform charge ρ L C m lies along the z-axis. Determine D at point P? D = Dρ aρ Q = ∫ ρ L dl but , Q = ∫ D • dS = Dρ ∫ dS = Dρ 2πρL ρL D= aρ 2πρ C. Infinite Sheet of Charge Consider the infinite sheet of uniform charge is ρS C/m2 D = DZ aZ ∫ρ ∫ D • dS ρ dS = D ( A + A ) ρ A = D (A + A ) Q = S dS , Q = S Z S D = Z ρS 2 aZ ρS Therefore , E = = aZ ε 0 2ε 0 D D. Uniformly Charged Sphere Gaussian surface for a uniformly charged sphere Q enc ∫ρ = = ρ v dv = ρ 2π v π ∫ ∫ ∫ φ θ =0 = ρ r v ∫ v dv r 2 sin θ drd θ d φ =0 r=0 4 πr 3 3 And ψ = ∫ D • dS = D = D 2π r π = D r 4π r ∫ dS r sin θ d θ d φ ∫ ∫ φ θ =0 r 2 =0 2 Hence , ψ = Qenc gives 4π r ρv D r 4π r = 3 Or .. 3 2 r D = ρ v ar 3 for 0 > r ≤ a r ≥ a, For Q enc ∫ρ = = ρ v dv = ρ 2π v r 2 dv sin θ drd θ d φ =0 r=0 4 πa 3 3 , While ψ = v a ∫ θ∫ ∫ φ =0 = ρ π ∫ v ∫ D • dS D r 4π r 2 = D r 4π r 4 = πa 3ρ 3 2 v Or .. a3 D = ρ va r 2 3r for r ≥ a D everywhere is given by: ⎧r a ρ ⎪3 v r D=⎨ 3 a ⎪ 2 ρ v ar ⎩ 3r 0<r ≤a r≥a