Download Torque and rotational inertia

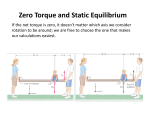
Torque and rotational inertia
We’ve seen one way of multiplying vectors is the dot product or the scalar product. For example,
A▪C = AxCx + AyCy = (4)(1) + (2)(-4) = -4
It can also be calculated: A▪C = |A|·|C|·cosθ = (4.47)(4.12)(cos257.5º) = -4
Another way of multiplying vectors is called the vector cross product, or simply cross product.
One way of finding this is with the determinant of a 3x3 matrix, but I will leave that until the end as an
optional appendix.
Instead, we’ll use an equation similar to one for dot products. For example, the cross product of A and
C, stated “A cross C” and written A x C equals |A|·|C|·sinθ. Again, |A| is the length of the A vector
which can be found by the Pythagorean Theorem, |C| is the length of the C vector, and θ is the angle
from the first vector to the second vector, swept counter-clockwise.
If you use inverse tangent, you will find A has an angle of 26.565º and C has an angle of 284º. So, to
sweep from A to C counter-clockwise would be to sweep an angle of about 257.5º.
Therefore, A x C = |A|·|C|·sinθ = (4.47)(4.12)(sin 257.5º) = -18
The cross product has the highest magnitude when θ is either 90º or 270º, so, conceptually, the cross
product is a measure of how perpendicular two vectors are. (Recall, the dot product was a measure of
how parallel two vectors are.)
There is another difference between the two. While the result of the dot product is a scalar, the result
of the cross product is a vector, meaning it has a direction. So what is the direction of our A x C
result? To answer this, you must use the right hand rule for cross products. What you do is this:
Physically take your right hand and, with palm flat, align the fingers with the first vector of the cross
product. In our example, this is vector A, so you align your fingers with A, pointing them at about 26º.
Then you sweep your fingers through the smaller path to hit the second vector. So you have a choice
between sweeping your fingers clockwise or counter-clockwise to hit the C vector, and the shorter path
is clockwise. When you make this sweep, you look at the direction of your thumb and this is the
direction of the cross product. In this case, your thumb points into the screen, which is the negative zaxis. This agrees with the negative sign in our answer of -18.
Note that if you were finding C x A, you would sweep from C to A along the shortest path. This
would be counter-clockwise, your thumb would point out of the screen along the positive z-axis, and
the cross product would be positive.
Understanding the cross product is valuable because the concept of torque is a cross product. By
definition, torque is the cross product of radius with force and is symbolized with the Greek letter tau.
τ = R x F = |R|·|F|·sinθ
Let’s use it in a few examples.
In the diagram above, a very light bar is balanced on a fulcrum. Let’s say the bar is 2m in length. A
red mass of 3kg hangs 80cm to the left of the fulcrum and a 2kg blue mass hangs 95cm to the right of
the fulcrum. What are the two torques applied?
Take the red mass first. The radius in the torque equation is the distance between the point of rotation
and where the force is being applied. Well, the point of rotation is the fulcrum and the force is being
applied to the bar where the cord is tied, 80cm from that fulcrum. So |R| = 0.8m.
The force at that point on the bar is going to come from the tension in the cord, which would be 29.4N,
so |F| = 29.4N.
What is the angle to use in sinθ? Well, it can help to draw the vectors for radius and force.
The radius, or radial vector, point from the point of rotation to where the force is applied. For the
tension of the red block this is to the left, or 180º. The force vector is down, or 270º, because the cord
pulls down on the thin beam.
Again the θ of sinθ is the angle from the first vector of the cross product (R) to the second vector (F),
swept counter-clockwise. If you look at the vector diagram on the right, you can see this is 90º.
So, τred block = (0.8m)(29.4N)(sin90º) = 23.52m·N
In what direction is this torque? Point your right hand with the radial vector, sweep your fingers to the
force vector along the shorter path, and see which way your thumb points. It should point out of the
page, along the +z axis, matching the positive value we calculated from the equation.
For the torque applied by the blue mass,
τblue block = (0.95m)(19.6N)(sin270º) = -18.62m·N
The net torque is simply the sum of the two torques, Στ = 4.9m·N
Because the net torque is positive, it will cause a positive angular acceleration, which is a counterclockwise angular acceleration.
Question 1: Suppose the red block has a mass of 3.5kg and hangs 50cm to the left of the fulcrum.
What torque does it apply?
Question 2: If the blue block is 1.8kg and hangs 60cm to the right of the fulcrum, what torque does it
apply?
Torque can also be used for common problems in statics, situations in where there is no linear or
rotational acceleration and usually no motion at all.
Let’s say two circus performers hold a uniform, 5m wooden plank which has a mass of 15kg. Standing
3m from the left end of the plank is an acrobat with a mass of 50kg.
What upward force must each circus worker apply to keep the system static?
Well, if we take the acrobat and plank as our system the total downward force from gravity with be
(65kg)(-9.8m/s2) = -637N. But how is this value going to be divided between the red hat and blue hat
workers? Your intuition might tell you that the blue hat worker will need to apply a greater force
because the acrobat is closer to him, and this will turn out to be true.
To get the exact values, we will use the concept of torque. Even though the system is not rotating, we
can still imagine a point around which it could rotate and take this to be our fulcrum. I generally take
the left hand side as my fulcrum, so let’s do that.
If we take where the red hat worker holds the plank as the fulcrum, what are the torques around that
fulcrum? Well, if the blue hat worker lets-go, clearly the system will rotate clockwise, so there must
be some clockwise torques coming from somewhere. They are coming from gravity on the acrobat
and gravity on the plank.
Using our equation for torque, let’s find the torque of the acrobat relative to our defined fulcrum.
τacrobat = |R|·|F|·sinθ = (3m)(490N)(sin270º) = -1470m·N
Even if the acrobat was not there and the blue hat worker let go, the plank would still rotate clockwise,
so there is a torque of gravity on the plank itself.
In fact, because the plank is spread throughout the x-dimension, there are many torques acting on the
many little bits of plank, each a different distance from the red hat worker. But because torque is a
linear equation, we can average out all of these distances and treat the mass of the plank as if it was
localized at its center. That means for a 5m plank, we will use an R value of 2.5m.
τplank = |R|·|F|·sinθ = (2.5m)(147N)(sin270º) = -367.5m·N
So we know the total clockwise torque is (-1470m·N) + (-367.5m·N) = -1837.5m·N, but we also know
the system is static, so the net torque is zero.
0 = -1837.5m·N + τblue hat
Therefore, the torque applied by the blue hat worker is +1837.5m·N. We can then solve for the force
he applies:
+1837.5m·N = (5m)(Fblue hat)(sin90º) and Fblue hat = 367.5N
We had already determined the total upwards force from both workers is +637N, so Fred hat = 269.5N.
Question 3: If the green hat acrobat stood in the middle of the plank, what force would the blue hat
man apply?
Suppose we have a simple system with a puck of mass m tied to a string of length R sitting on a
frictionless table:
Now let’s say you push on the puck with a force of F (in a direction of 90º relative to the diagram).
F = m·a
and from a previous derivation, a = α·R, so
F = m·α·R
We can also multiply both sides by R to get
R·F = [m·R2]·α
or
τ = [m·R2]·α
Clearly, the angular acceleration is proportional to the torque applied and inversely proportional to this
bracket of [m·R2].
The bracket therefore represents the resistance to angular acceleration and is called the rotational
inertia, I.
The same way masses can be added together, rotational inertias can be added together, so
Isystem = 𝑚1 𝑅12 + 𝑚2 𝑅22 + 𝑚3 𝑅32 + …… = ∑ 𝑚 · 𝑅 2
This is true for point masses or masses which are small relative to the radius in which they move.
If the mass is distributed through space, like a disk that spins around itself, then calculus notation must
be used:
I = ∫ 𝑅 2 · 𝑑𝑚
Also, torque is a vector and vectors can be added together, so we can write τ = [m·R2]·α as
τ = I·α
where τ implies net torque
This is the rotational analog of F = m·a
So let’s use I = ∫ 𝑅 2 · 𝑑𝑚 in an example:
In the diagram above is a long, thin bar of length L and mass m which is free to swing into and out of
the page around the vertical axis. What is the rotational inertia of this bar?
We imagine cutting the bar up into many small sections, finding the rotational inertia of each section,
and then adding all of those values.
The trick we need is to either write R in terms of m or m in terms of R. We’ll do the latter with the
concept of linear mass density, λ.
By definition, linear mass density is the mass of the bar divided by the length of the bar, λ =
𝑚
𝐿
If this is true, then dm = λ·dL
Stepping from left to right along the bar, a little step of distance equals a little step of the bar’s length,
so dL = dR and, therefore, dm = λ·dR.
Now we can integrate:
I = ∫ 𝑅 2 · 𝑑𝑚 = ∫ 𝑅 2 · 𝜆 · 𝑑𝑅 with the boundaries being zero at the point of rotation and L at the end of
the bar. Lambda is a constant which can be pulled outside the integral.
𝐿
I =λ ∫0 𝑅 2 · 𝑑𝑅
1
I = (λ)(3L3)
where λ =
𝑚
𝐿
1
so Ibar = 3ML2
Question 4: Around its end, what is the rotational inertia of a 1.6kg bar with a length of 1.5m?
However, this is specific to the bar rotated around its end. If the bar was spinning around its center,
𝐿
𝐿
1
the integral boundaries would be - 2 and + 2 and the result would be Ibar = 12ML2
A more general method of finding rotational inertias when the axis shifts around the body is to use the
parallel axis theorem. This equation is written as:
I = Icm + M·h2
This is read: the rotational inertia for any object is equal to the rotational inertia through the center of
mass of that object plus a second term, the mass of the object times h, where h is the distance between
the center of mass of the object and the axis of rotation.
So let’s just see how this works for the bar. We know the bar’s rotational inertia through its center of
1
mass is 12ML2, so that’s the first term in the parallel axis theorem. What if the bar was rotating around
𝐿
its end? Then h would be 2 as this is the distance between the center of mass of the bar and our chosen
axis of rotation.
1
𝐿
Then I = 12ML2 + M(2)2
result.
and this becomes
1
I = 3ML2
in agreement with the previous
Our chart relating linear motion and rotational motion can then be continued:
Linear kinematics concept
Linear position – s
Linear velocity – v
Rotational kinematics concept
Angular position – θ
Angular velocity – ω
Linear acceleration – a
Angular acceleration – α
Force: F
Mass: m
F = m·a
Torque: τ = R x F
Rotational inertia: I = ∑ 𝑚 · 𝑅 2 or ∫ 𝑅 2 · 𝑑𝑚
τ = I·α
1
Additionally, if ΣK = 2m·v2 and, for rotating particles, v = ω·R, then
1
1
1
1
ΣK = 2m·v2 = 2m(ω·R)2 = 2[Σ m·R2]·ω2 = 2I·ω2
And in the same way we defined linear work as F▪Δs, we can define rotational work as τ ▪Δθ.
An input of rotational work to a system can cause a change in its rotational kinetic energy by:
τ ▪Δθ = (I·α)▪
𝝎𝟐𝒇 − 𝝎𝟐𝒊
𝟐·𝜶
1
1
= 2I·ωf2 - 2I·ωi2 = ΔKrotational
Linear kinematics concept
1
Linear kinetic energy: K = 2m·v2
Linear work: W = F▪Δs
Rotational kinematics concept
1
Rotational kinetic energy: K = 2I·ω2
Rotational work: W = τ▪Δθ
To review:
τ = R x F = |R|·|F|·sinθ
R is the distance between the point around which the system rotates and the point at which the force is
applied
F is the force applied at that point
θ is the angle swept out from the R vector to the F vector, counter-clockwise. The R vector points
from the point of rotation to where the force is applied. The F vector points in the direction in which
the force is applied.
If the radii and forces are in the xy-plane, then the torques will be along the z-axis, either into (-) or out
of (+) the screen. The right hand rule for cross products can confirm the correct sign.
In statics problems, take a point in the system where a force is applied and treat it as the fulcrum for a
potential rotation. Set the net torque around this point to zero and solve.
τ = I·α
where I = ∑ 𝑚 · 𝑅 2
for point masses and
I = ∫ 𝑅 2 · 𝑑𝑚 for non-point masses
1
Krotation = 2I·ω2
Wrotation = τ·Δθ
Appendix – cross product as a matrix determinant
Let’s take a simple example:
Here the force vector is 10N in the y-dimension and the radial vector is 5m in the x-dimension.
Written as a matrix, the cross product is:
𝑖̂
𝑅𝑥
𝐹𝑥
𝑗̂
𝑅𝑦
𝐹𝑦
𝑘̂
𝑅𝑧
𝐹𝑧
Filled-in with the example above, it would become:
𝑖̂
5𝑚
0
𝑗̂
0
10𝑁
𝑘̂
0
0
The determinant is simply (50m·N)𝑘̂ and this is the torque. You can see this agrees with our previous
method of determining the torque, (5m)(10N)(sin90º) and the right hand rule.