Download lecture 24

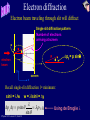
Physics 102: Lecture 23
De Broglie Waves, Uncertainty, and Atoms
Physics 102: Lecture 23, Slide 1
Three Early Indications of Problems
with Classical Physics
• Blackbody radiation
• Photoelectric effect
• Wave-particle duality
Lecture 22:
Quantum Mechanics
• Compton scattering
• DeBroglie
• Heisenberg Uncertainty Principle
Physics 102: Lecture 23, Slide 2
Today
Compton Scattering
This experiment really shows photon momentum!
Pincoming photon + 0 = Poutgoing photon + Pelectron
Electron at
rest
Incoming photon has
momentum p, and
wavelength 
Photon energy
E  hf 
Physics 102: Lecture 23, Slide 3
hc

Photon momentum
p
h

Experiment: Outgoing
photon has longer
wavelength 
Recoil electron carries
some momentum and KE
 E = pc
Compton Scattering
• Incident photon loses momentum, since it
transfers momentum to the electron
• Lower momentum means longer wavelength
• This is proof that a photon has momentum
p
Physics 102: Lecture 23, Slide 4
h

Is Light a Wave or a Particle?
• Wave
– Electric and Magnetic fields act like waves
– Superposition, Interference, and Diffraction
• Particle
– Photons
– Collision with electrons in photo-electric effect
– Compton scattering from electrons
BOTH Particle AND Wave
Physics 102: Lecture 23, Slide 5
ACT: Photon Collisions
Photons with equal energy and momentum hit both
sides of the plate. The photon from the left sticks
to the plate, the photon from the right bounces off
the plate. What is the direction of the net impulse
on the plate?
1) Left
Physics 102: Lecture 23, Slide 6
2) Right
3) Zero
Radiometer
Incident photons
Black side
(absorbs)
Shiny side
(reflects)
Preflight 23.1
Photon A strikes a black surface and is absorbed. Photon B
strikes a shiny surface and is reflected back. Which photon
imparts more momentum to the surface?
Photon A
Physics 102: Lecture 23, Slide 7
Photon B
Ideal Radiometer
Photons bouncing off shiny side and sticking
to black side. Shiny side gets more momentum
so it should rotate with the black side leading
Physics 102: Lecture 23, Slide 8
Our Radiometer
Black side is hotter: gas molecules bounce off it with
more momentum than on shiny side-this is a bigger
effect than the photon momentum
Physics 102: Lecture 23, Slide 9
Electrons are Particles and Waves!
• Depending on the experiment electron can behave
like
– wave (interference)
– particle (localized mass and charge)
• Recall Young’s double slit experiment:
– If we measure which slit the electron went through,
then there is no interference pattern!!
Physics 102: Lecture 23, Slide 10
De Broglie Waves
p
h

h

p
So far only photons have wavelength, but De Broglie
postulated that it holds for any object with momentum- an
electron, a nucleus, an atom, a baseball,…...
Explains why we can see
interference and diffraction for
material particles like electrons!!
Physics 102: Lecture 23, Slide 11
Preflight 23.3
Which baseball has the longest De Broglie wavelength?
(1)
A fastball (100 mph)
(2)
A knuckleball (60 mph)
(3)
Neither - only curveballs have a wavelength
Physics 102: Lecture 23, Slide 12
ACT: De Broglie Wavelength
A stone is dropped from the top of a building.
What happens to the de Broglie wavelength of the
stone as it falls?
1. It decreases
2. It stays the same
3. It increases
Physics 102: Lecture 23, Slide 13
Some Numerology
Standard units (m, kg, s) are not convenient for
talking about photons & electrons
• 1 eV = energy gained by a charge +e when
accelerated through a potential difference of 1 Volt
– e = 1.6 x 10-19 C so 1 eV = 1.6 x 10-19 J
• h = 6.626 x 10-34 J·sec
• c = 3 x 108 m/s
– hc = 1.988 x 10-25 J·m = 1240 eV·nm
• mass of electron m = 9.1 x 10-34 kg
– mc2 = 8.2 x 10-13 J = 511,000 eV = 511 keV
Physics 102: Lecture 23, Slide 14
Comparison:
Equations are different - be careful!
Wavelength of Photon vs. Electron
You have a photon and an electron, both with 1 eV of energy. Find
the de Broglie wavelength of each.
•
Photon with 1 eV energy:
E
hc

 
hc 1240 eV nm

 1240 nm
E
1 eV
• Electron with 1 eV kinetic energy:
2
1
p
KE  mv 2 and p = mv, so KE =
2
2m
Solve for p  2m(K.E.)
Big difference!
h
1240 eV nm
hc



2
2m(KE)
2(511,000 eV)(1 eV)
2mc (KE)
Physics 102: Lecture 23, Slide 15
 1.23nm
X-ray vs. electron diffraction
X-ray diffraction
e– diffraction
Demo
Identical pattern emerges if de Broglie wavelength of
e– equals the X-ray wavelength!
Physics 102: Lecture 23, Slide 16
From College Physics, Vol. Two
Preflights 23.4, 23.5
Photon A has twice as much momentum as Photon B. Compare
their energies.
•
EA = EB
• EA = 2 EB
•
EA = 4 EB
Electron A has twice as much momentum as Electron B. Compare
their energies.
•
EA = EB
• EA = 2 EB
•
EA = 4 EB
Physics 102: Lecture 23, Slide 17
ACT: De Broglie
Compare the wavelength of a bowling ball
with the wavelength of a golf ball, if each
has 10 Joules of kinetic energy.
(1) bowling > golf
(2) bowling = golf
(3) bowling < golf
Physics 102: Lecture 23, Slide 18
Heisenberg Uncertainty Principle
Recall: Quantum Mechanics tells us nothing is
certain, everything is probability
h
p y y 
2
Uncertainty in
momentum (along y)
Uncertainty in
position (along y)
Rough idea: if we know momentum very precisely,
we lose knowledge of location, and vice versa.
Physics 102: Lecture 23, Slide 19
Electron diffraction
Electron beam traveling through slit will diffract
Single slit diffraction pattern
Number of electrons
arriving at screen
w
q
q
electron
beam
py = p sinq
y
x
screen
Recall single-slit diffraction 1st minimum:
sinq = /w
w = /sinq = y
p y y  p sin q
Physics 102: Lecture 23, Slide 20

sin q
 p  h
Using de Broglie 
Number of electrons
arriving at screen
py
w
electron
beam
py w  h
y
x screen
Electron entered slit with momentum along x direction and no
momentum in the y direction. When it is diffracted it acquires a py
which can be as big as h/w.
The “Uncertainty in py” is
py  h/w.
An electron passed through the slit somewhere along the y
direction. The “Uncertainty in y” is y  w.
 p y  y  h
Physics 102: Lecture 23, Slide 21
py
Number of electrons
arriving at screen
w
electron
beam
 p y  y  h
y
x screen
If we make the slit narrower (decrease w =y) the diffraction
peak gets broader (py increases).
“If we know location very precisely, we lose knowledge of
momentum, and vice versa.”
Physics 102: Lecture 23, Slide 22
h
p y y 
2
to be precise...
Of course if we try to locate the position of the particle along the x axis
to x we will not know its x component of momentum better than px,
where
h
p x x 
2
and the same for z.
Preflight 23.7
According to the H.U.P., if we know the x-position of a particle, we
can not know its:
(1)
y-position
(2)
x-momentum
(3)
y-momentum
(4)
Energy
Physics 102: Lecture 23, Slide 23