* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download lecture 24
Wave packet wikipedia , lookup
Monte Carlo methods for electron transport wikipedia , lookup
Bremsstrahlung wikipedia , lookup
Quantum vacuum thruster wikipedia , lookup
Angular momentum operator wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Elementary particle wikipedia , lookup
Peter Kalmus wikipedia , lookup
Compact Muon Solenoid wikipedia , lookup
Renormalization wikipedia , lookup
Renormalization group wikipedia , lookup
Photoelectric effect wikipedia , lookup
Uncertainty principle wikipedia , lookup
Future Circular Collider wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Wheeler's delayed choice experiment wikipedia , lookup
Delayed choice quantum eraser wikipedia , lookup
Double-slit experiment wikipedia , lookup
Introduction to quantum mechanics wikipedia , lookup
Photon polarization wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
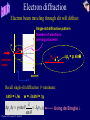
Physics 102: Lecture 23 De Broglie Waves, Uncertainty, and Atoms Physics 102: Lecture 23, Slide 1 Three Early Indications of Problems with Classical Physics • Blackbody radiation • Photoelectric effect • Wave-particle duality Lecture 22: Quantum Mechanics • Compton scattering • DeBroglie • Heisenberg Uncertainty Principle Physics 102: Lecture 23, Slide 2 Today Compton Scattering This experiment really shows photon momentum! Pincoming photon + 0 = Poutgoing photon + Pelectron Electron at rest Incoming photon has momentum p, and wavelength Photon energy E hf Physics 102: Lecture 23, Slide 3 hc Photon momentum p h Experiment: Outgoing photon has longer wavelength Recoil electron carries some momentum and KE E = pc Compton Scattering • Incident photon loses momentum, since it transfers momentum to the electron • Lower momentum means longer wavelength • This is proof that a photon has momentum p Physics 102: Lecture 23, Slide 4 h Is Light a Wave or a Particle? • Wave – Electric and Magnetic fields act like waves – Superposition, Interference, and Diffraction • Particle – Photons – Collision with electrons in photo-electric effect – Compton scattering from electrons BOTH Particle AND Wave Physics 102: Lecture 23, Slide 5 ACT: Photon Collisions Photons with equal energy and momentum hit both sides of the plate. The photon from the left sticks to the plate, the photon from the right bounces off the plate. What is the direction of the net impulse on the plate? 1) Left Physics 102: Lecture 23, Slide 6 2) Right 3) Zero Radiometer Incident photons Black side (absorbs) Shiny side (reflects) Preflight 23.1 Photon A strikes a black surface and is absorbed. Photon B strikes a shiny surface and is reflected back. Which photon imparts more momentum to the surface? Photon A Physics 102: Lecture 23, Slide 7 Photon B Ideal Radiometer Photons bouncing off shiny side and sticking to black side. Shiny side gets more momentum so it should rotate with the black side leading Physics 102: Lecture 23, Slide 8 Our Radiometer Black side is hotter: gas molecules bounce off it with more momentum than on shiny side-this is a bigger effect than the photon momentum Physics 102: Lecture 23, Slide 9 Electrons are Particles and Waves! • Depending on the experiment electron can behave like – wave (interference) – particle (localized mass and charge) • Recall Young’s double slit experiment: – If we measure which slit the electron went through, then there is no interference pattern!! Physics 102: Lecture 23, Slide 10 De Broglie Waves p h h p So far only photons have wavelength, but De Broglie postulated that it holds for any object with momentum- an electron, a nucleus, an atom, a baseball,…... Explains why we can see interference and diffraction for material particles like electrons!! Physics 102: Lecture 23, Slide 11 Preflight 23.3 Which baseball has the longest De Broglie wavelength? (1) A fastball (100 mph) (2) A knuckleball (60 mph) (3) Neither - only curveballs have a wavelength Physics 102: Lecture 23, Slide 12 ACT: De Broglie Wavelength A stone is dropped from the top of a building. What happens to the de Broglie wavelength of the stone as it falls? 1. It decreases 2. It stays the same 3. It increases Physics 102: Lecture 23, Slide 13 Some Numerology Standard units (m, kg, s) are not convenient for talking about photons & electrons • 1 eV = energy gained by a charge +e when accelerated through a potential difference of 1 Volt – e = 1.6 x 10-19 C so 1 eV = 1.6 x 10-19 J • h = 6.626 x 10-34 J·sec • c = 3 x 108 m/s – hc = 1.988 x 10-25 J·m = 1240 eV·nm • mass of electron m = 9.1 x 10-34 kg – mc2 = 8.2 x 10-13 J = 511,000 eV = 511 keV Physics 102: Lecture 23, Slide 14 Comparison: Equations are different - be careful! Wavelength of Photon vs. Electron You have a photon and an electron, both with 1 eV of energy. Find the de Broglie wavelength of each. • Photon with 1 eV energy: E hc hc 1240 eV nm 1240 nm E 1 eV • Electron with 1 eV kinetic energy: 2 1 p KE mv 2 and p = mv, so KE = 2 2m Solve for p 2m(K.E.) Big difference! h 1240 eV nm hc 2 2m(KE) 2(511,000 eV)(1 eV) 2mc (KE) Physics 102: Lecture 23, Slide 15 1.23nm X-ray vs. electron diffraction X-ray diffraction e– diffraction Demo Identical pattern emerges if de Broglie wavelength of e– equals the X-ray wavelength! Physics 102: Lecture 23, Slide 16 From College Physics, Vol. Two Preflights 23.4, 23.5 Photon A has twice as much momentum as Photon B. Compare their energies. • EA = EB • EA = 2 EB • EA = 4 EB Electron A has twice as much momentum as Electron B. Compare their energies. • EA = EB • EA = 2 EB • EA = 4 EB Physics 102: Lecture 23, Slide 17 ACT: De Broglie Compare the wavelength of a bowling ball with the wavelength of a golf ball, if each has 10 Joules of kinetic energy. (1) bowling > golf (2) bowling = golf (3) bowling < golf Physics 102: Lecture 23, Slide 18 Heisenberg Uncertainty Principle Recall: Quantum Mechanics tells us nothing is certain, everything is probability h p y y 2 Uncertainty in momentum (along y) Uncertainty in position (along y) Rough idea: if we know momentum very precisely, we lose knowledge of location, and vice versa. Physics 102: Lecture 23, Slide 19 Electron diffraction Electron beam traveling through slit will diffract Single slit diffraction pattern Number of electrons arriving at screen w q q electron beam py = p sinq y x screen Recall single-slit diffraction 1st minimum: sinq = /w w = /sinq = y p y y p sin q Physics 102: Lecture 23, Slide 20 sin q p h Using de Broglie Number of electrons arriving at screen py w electron beam py w h y x screen Electron entered slit with momentum along x direction and no momentum in the y direction. When it is diffracted it acquires a py which can be as big as h/w. The “Uncertainty in py” is py h/w. An electron passed through the slit somewhere along the y direction. The “Uncertainty in y” is y w. p y y h Physics 102: Lecture 23, Slide 21 py Number of electrons arriving at screen w electron beam p y y h y x screen If we make the slit narrower (decrease w =y) the diffraction peak gets broader (py increases). “If we know location very precisely, we lose knowledge of momentum, and vice versa.” Physics 102: Lecture 23, Slide 22 h p y y 2 to be precise... Of course if we try to locate the position of the particle along the x axis to x we will not know its x component of momentum better than px, where h p x x 2 and the same for z. Preflight 23.7 According to the H.U.P., if we know the x-position of a particle, we can not know its: (1) y-position (2) x-momentum (3) y-momentum (4) Energy Physics 102: Lecture 23, Slide 23





























![L 35 Modern Physics [1]](http://s1.studyres.com/store/data/001036078_1-1a4f17b9367db590f7dcb987ef21bbe6-150x150.png)

