* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download KEY - Rose
History of electromagnetic theory wikipedia , lookup
Time in physics wikipedia , lookup
Electromagnetism wikipedia , lookup
Speed of gravity wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
History of quantum field theory wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Lorentz force wikipedia , lookup
Maxwell's equations wikipedia , lookup
Mathematical formulation of the Standard Model wikipedia , lookup
Field (physics) wikipedia , lookup
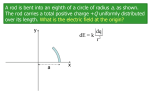
Physics II Homework VII CJ Chapter 26; 8, 18, 21, 25, 32, 45, 48, 54 26.8. Model: The rods are thin. Assume that the charge lies along a line. Visualize: Because both the rods are positively charged, the electric field from each rod points away from the rod. Because the electric fields from the two rods are in opposite directions at P 1, P2, and P3, the net field strength at each point is the difference of the field strengths from the two rods. Solve: Example 26.3 gives the electric field strength in the plane that bisects a charged rod: Erod Q 1 4 0 r r 2 L / 2 2 The electric field from the rod on the right at a distance of 1 cm from the rod is Eright 9.0 109 N m2 /C2 10 109 C 0.01 m 0.01 m 0.05 m 2 2 1.765 105 N/C The electric field from the rod on the right at distances 2 cm and 3 cm from the rod are 0.835 105 N/C and 0.514 105 N/C. The electric fields produced by the rod on the left at the same distances are the same. Point P1 is 1.0 cm from the rod on the left and is 3.0 cm from the rod on the right. Because the electric fields at P 1 have opposite directions, the net electric field strengths are At 1.0 cm E 1.765 105 N/C 0.514 105 N/C 1.25 105 N/C At 2.0 cm E 0.835 105 N/C 0.835 105 N/C 0 N/C At 3.0 cm E 1.765 105 N/C 0.514 105 N/C 1.25 105 N/C 26.18. Model: A spherical shell of charge Q and radius R has an electric field outside the sphere that is exactly the same as that of a point charge Q located at the center of the sphere. Visualize: In the case of a metal ball, the charge resides on its surface. This can then be visualized as a charged spherical shell of radius R. Solve: Equation 26.28 gives the electric field of a charged spherical shell at a distance r > R: Eball In the present case, Eball 50,000 N/C at r Q 4 0 r Eball 2 1 2 Q rˆ 4 0 r 2 10 cm 2.0 cm 7.0 cm 0.07 m . So, 0.07 m 2 50,000 N/C 9.0 10 N m2 /C2 9 2.72 10 8 C 27.2 nC 26.21. Model: The electric field in a region of space between two charged circular disks is uniform. Solve: The electric field strength inside the capacitor is E Q 0 A . Thus, the area is A 1.5 109 1.6 10 19 C Q D2 2.71 104 m2 12 2 2 5 0E 4 8.85 10 C /N m 1.0 10 N/C 4A D 1.86 cm Assess: As long as the spacing is much less than the plate dimensions, the electric field is independent of the spacing and depends only on the diameter of the plates. 26.25. Model: The electric field is uniform, so the electrons will have a constant acceleration. Visualize: Solve: A constant-acceleration kinematic equation of motion is v v 2a x 2 1 2 0 5.0 10 7 m/s 0 m/s v2 v02 a 1 1.042 1017 m/s2 2x 2 1.2 10 2 m 2 2 The net force on the electron in the electric field is F qE ma . Thus, E 9.11 1031 kg 1.042 1017 m/s2 ma 5.93 105 N/C q 1.60 10 19 C Hence, the field strength is 5.93 10 5 N/C. 26.32. Model: The electric field is that of three point charges q1, q2 and q3. Visualize: Please refer to Figure P26.32. Assume the charges are in the x-y plane. The 5 nC charge is q1, the bottom 10 nC charge is q3, and the top 10 nC charge is q2. The net electric field at the dot is Enet E1 E2 E3 . The procedure will be to find the magnitudes of the electric fields, to write them in component form, and to add the components. Solve: The electric field produced by q1 is E1 1 q1 4 0 r 2 1 9.0 10 9 N m2 /C2 5.0 10 9 C 0.02 m 2 112,500 N/C E1 points toward q1, so in component form E1 112,500 ˆj N/C . The electric field produced by q2 is E2 56,250 N/C. E2 points away from q2, so E 56,250iˆ N/C . Finally, the electric field produced by q3 is 2 E3 1 q3 9.0 10 9 N m2 /C2 10.0 10 9 C 45,000 N/C 0.02 m 0.04 m E3 points away from q3 and makes an angle tan1 2/ 4 26.57 with the x-axis. So, 4 0 r 2 3 2 2 E3 E3 cos iˆ E3 sin ˆj 40,250iˆ 20,130 ˆj N/C Adding these three vectors gives Enet E1 E2 E3 96,500iˆ 92,400 ˆj N/C This is in component form. The magnitude of the field is Enet Ex2 Ey2 96,500 N/C 92,400 N/C 2 2 133,600 N/C and its angle from the x-axis is tan1 Ex Ey 43.8 . We can also write Enet 133,600 N/C, 43.8 below the x -axis . 26.45. Model: The electric field is that of a line charge of length L. Visualize: Please refer to Figure P26.45. Let the bottom end of the rod be the origin of the coordinate system. Divide the rod into many small segments of charge q and length y. Segment i creates a small electric field at the point P that makes an angle with the horizontal. The field has both x and y components, but Ez 0 N/C. The distance to segment i from point P is x 2 y2 Solve: 12 . The electric field created by segment i at point P is Ei q cos iˆ sin ˆj 4 x y 4 x y q 2 2 2 2 0 0 x x 2 y 2 iˆ ˆj x 2 y2 y The net field is the sum of all the E i , which gives E Ei . q is not a coordinate, so before converting the sum to an i integral we must relate charge q to length y. This is done through the linear charge density Q/L, from which we have the relationship q y Q y L With this charge, the sum becomes E Q/ L x y 2 2 4 0 i x y 3/ 2 iˆ x yy 2 y 2 3/ 2 ˆj Now we let y dy and replace the sum by an integral from y 0 m to y L . Thus, Q / L L E xdy 4 0 0 x 2 y2 Q 1 4 0 x x L 2 2 ydy L iˆ 3/ 2 iˆ 0 x 2 y2 3/ 2 1 Q 1 4 0 Lx y ˆj Q / L x 4 0 x 2 x 2 y2 L 1 iˆ x 2 y2 0 L 0 ˆj ˆ j x L x 2 2 26.48. Model: Assume that the semicircular rod is thin and that the charge lies along the semicircle of radius R. Visualize: The origin of the coordinate system is at the center of the circle. Divide the rod into many small segments of charge q and arc length s. Segment i creates a small electric field E i at the origin. The line from the origin to segment i makes an angle with the x-axis. Solve: Because every segment i at an angle above the axis is matched by segment j at angle below the axis, the y-components of the electric fields will cancel when the field is summed over all segments. This leads to a net field pointing to the right with Ex Ei x Ei cos i i Ey 0 N/C i Note that angle i depends on the location of segment i. Now all segments are at the same distance ri R from the origin, so q q 4 0 ri2 4 0 R2 Ei The linear charge density on the rod is Q/L, where L is the rod’s length. This allows us to relate charge q to the arc length s through q s (Q/L)s Thus, the net field at the origin is Ex i Q / L s cos 4 0 R 2 i Q 4 0 LR2 cos s i i The sum is over all the segments on the rim of a semicircle, so it will be easier to use polar coordinates and integrate over rather than do a two-dimensional integral in x and y. We note that the arc length s is related to the small angle by s R, so Ex Q 4 0 LR cos i i With d, the sum becomes an integral over all angles forming the rod. varies from /2 to /2. So we finally arrive at Ex Q 4 0 /2 LR /2 cos d Q 4 0 LR sin /2 / 2 2Q 4 0 LR Since we’re given the rod’s length L and not its radius R, it will be convenient to let R L/. So our final expression for E , now including the vector information, is E 1 2 Q ˆ i 4 0 L2 26.54. Model: Assume that the electric field inside the capacitor is constant, so constant-acceleration kinematic equations apply. Visualize: Please refer to Figure P26.54. Solve: (a) The force on the electron inside the capacitor is F ma qE a qE m Because E is directed upward (from the positive plate to the negative plate) and q 1.60 10 19 C , the acceleration of the electron is downward. We can therefore write the above equation as simply ay qE/m. To determine E, we must first find ay. From kinematics, x1 x0 v0 x t1 t0 21 ax t1 t0 0.04 m 0 m v0 cos45 t1 t0 0 m 2 t1 t0 0.04 m 5.0 10 6 m/s cos45 1.1314 10 8 s Using the kinematic equations for the motion in the y direction, t t v1y v0 y ay 1 0 2 qE t1 t0 0 m/s v0 sin45 m 2 E 2 9.1 10 31 kg 5.0 10 6 m/s sin 45 2 m v0 sin 45 3550 N/C q t1 t0 1.60 10 19 C 1.1314 10 8 s (b) To determine the separation between the two plates, we note that y0 0 m and v0 y 5.0 106 m/s sin 45 , but at y y1, the electron’s highest point, v1y 0 m/s. From kinematics, v12y v02y 2ay y1 y0 0 m2 / s2 v02 sin2 45 2ay y1 y0 y1 y0 v02 sin2 45 v2 0 2ay 4ay From part (a), ay 1.60 10 19 C 3550 N/C qE 6.242 1014 m/s2 m 9.1 10 31 kg y1 y0 5.0 10 6 m/s 2 4 6.242 1014 m/s2 0.010 m 1.0 cm This is the height of the electron’s trajectory, so the minimum spacing is 1.0 cm.