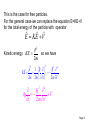* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download QM L-6
Measurement in quantum mechanics wikipedia , lookup
Identical particles wikipedia , lookup
Nuclear structure wikipedia , lookup
Coherent states wikipedia , lookup
Perturbation theory (quantum mechanics) wikipedia , lookup
Quantum state wikipedia , lookup
Quantum logic wikipedia , lookup
Matrix mechanics wikipedia , lookup
Angular momentum operator wikipedia , lookup
Oscillator representation wikipedia , lookup
Uncertainty principle wikipedia , lookup
Introduction to quantum mechanics wikipedia , lookup
Quantum tunnelling wikipedia , lookup
Old quantum theory wikipedia , lookup
Tensor operator wikipedia , lookup
Density matrix wikipedia , lookup
Renormalization group wikipedia , lookup
Dirac equation wikipedia , lookup
Path integral formulation wikipedia , lookup
Canonical quantization wikipedia , lookup
Probability amplitude wikipedia , lookup
Photon polarization wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Wave function wikipedia , lookup
Wave packet wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Eigenstate thermalization hypothesis wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
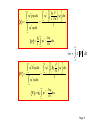
Quantum Mechanics Lecture-6 Reference: Concept of Modern Physics by “A. Beiser” Page 1 Expectation Values In the case of SWE , wave function gives the information in terms of probabilities and not specific numbers. Therefore, instead of finding the average value of any term (for example position of particle x ), we find the expectation value <x> of that. Ni xi Now, x Ni We replace the number N i of particles at xi by the probability Pi dx that the particle be found in an interval dx at xi and summation by integration. <x> x 2 dx 2 dx Page 2 The denominator equals the probability that the particle exists some where between x= to x= and therefore it is equal to 1. So expectation value for position is <x> = x 2 dx The same procedure can be used to obtain expectation value of any quantity : Potential energy V(x) which is a function of x. The expectation value for ‘p’ can not be calculated this way. According to uncertainty principle: Page 3 If we specify x, so x 0 , we can not specify a corresponding p since xp / 2. The same problem occurs for the expectation value of E. OPERATORS: A proper way to evaluate expectation values for p and E comes from differentiating free particle wave function (x , t) = A e-(2i/h)(Et-px) 2 i i p p p i x x h 2 i i E i E E t t h Page 4 i x E i t p Looking at this we can say that quantity p corresponds to i differential operator and E to t . Thus the operator i x instructs us to take partial derivative of function that comes after it. p̂ i x So momentum operator : And total energy operator: i or i pˆ x ˆ E t Page 5 This is the case for free particles. For the general case we can replace the equation E=KE+V for the total energy of the particle with operator Eˆ KEˆ Vˆ p2 Kinetic energy KE so we have 2m 2 2 2 ˆ p 1 KEˆ 2m 2m i x 2m x 2 2 i V 2 t 2m x 2 2 Page 6 Now we multiply the equation with we get 2 2 i V 2 t 2m x which is the SWE. Because p and E can be replaced by their corresponding operators in an equation, we can use these to obtain their expectation values. p̂ i x i ˆ E t Page 7 p *p̂dx *dx * i x dx 1 p i * dx x <x> = E *Êdx *dx * i t dx 1 x 2 dx E i * dx t Page 8 Let us see why expectation values involving operators have to be expressed in the form (x , t) = A e-(2i/h)(Et-px) p ˆ dx *p The other alternatives are * * ˆ dx p p dx 0 i x i * since *and must be 0 at x= p ˆ dx p * i * and dx x which makes no sense. Page 9 EIGENVALUES and EIGNFUNCTIONS Schrödinger's time independent wave equation h 2 d 2 - 2 V E 2 8 m dx d 2 82 m 2 (E V) 0 2 dx h This is the ‘steady state or ‘timeindependent’ form of Schrödinger equation. Note: Wave function independent.-------- Ψ(x). is time The values of energy En for which, this steady state equation can be solved are called eigen values. Page 10 and the corresponding wave functions are called eigen functions. Now, 2 h 2 d 2 2 - 2 V E or E V 2 2 8 m dx 2m x So total energy operator can also be written as Ĥ V 2 2m x 2 2 Page 11 Therefore, Hˆ n En n So we can say that the values En are the eigenvalues of the Hamiltonian operator H. The function n is called eigen function. So we can summarize the various operators used in Q.M Page 12 Position x xˆ x x Linear Momentum p x pˆ x i Momentum in 3D p pˆ i ˆ EEi t 2 2 2 p̂ KEˆ 2m 2m x 2 ˆ V(x) V(x) V(x) Total Energy Kinetic Energy Potentail Energy Total Energy 2 p̂ ˆ [ HH V] 2m (Hamiltonian form) Page 13 Example: function sin 2x d2 operator 2 dx eigenvalue ? Solution: d2 2 (sin 2x) 4(sin 2x) dx eigenvalue Note: In Quantum mechanics, the allowed eigenfunction 1. must be finite for all x 2. must be single-valued for all x 3. must be continuous for all x Page 14 Condition of normalized wavefunction d 1 * 1 or 1 d 1 * 2 2 1 and 2 called normalized wavefunction. Condition for orthogonal wavefunction * 21d 0 or d 0 * 1 2 wavefunction 1 and 2 are mutually orthogonal Condition of orthonormal function * i jd 0 =1 if i j if i = j Page 15