Download Lecture Set 3 Gauss`s Law

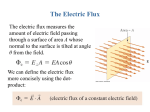
Chapter 23
Gauss’s Law
Summer 2008
Chapter 23
Gauss’ law
In this chapter we will introduce the following new concepts:
Symmetry
Gauss’ law
The flux (symbol Φ ) of the electric field.
We will then apply Gauss’ law and determine the electric field
generated by:
An infinite, uniformly charged insulating plane.
An infinite, uniformly charged insulating rod.
A uniformly charged spherical shell.
A uniform spherical charge distribution.
We will also apply Gauss’ law to determine the electric field inside and
outside charged conductors.
(23-1)
Last Time: Definition – Sort of –
Electric Field Lines
Field Lines  Electric Field
Last time we showed that
Ignore the Dashed Line …
Remember last time .. the big plane?
s/2e0
s/2e0
E=0
s/2e0
s/2e0
s/2e0
s/2e0
E=s/e0
We will use this a lot!
E=0
NEW RULES





Imagine a region of space where the ELECTRIC
FIELD LINES HAVE BEEN DRAWN.
The electric field at a point in this region is
TANGENT to the Electric Field lines that have been
drawn.
If you construct a small rectangle normal to the field
lines, the Electric Field is proportional to the number
of field lines that cross the small area.
The DENSITY of the lines.
We won’t use this much
n̂
n̂
So far …



The electric field exiting a closed surface
seems to be related to the charge inside.
But … what does “exiting a closed surface
mean”?
How do we really talk about “the electric field
exiting” a surface?


How do we define such a concept?
CAN we define such a concept?
Mr. Gauss
answered the
question with..
The “normal component” of the
ELECTRIC FIELD
E
n
En = E cos( )n
En = E cos( ) n = E  n
En
DEFINITION FLUX
E
n
En
Flux = E n A = (E  n)A
 = E A cos( )
“Element” of Flux of a vector E
leaving a surface
d = E  dA = E NORMAL  A
also
d = E  dA = E  ndA
For a CLOSED surface:
n is a unit OUTWARD pointing vector.
Definition of TOTAL FLUX through
a surface
 =  d
surface
Total Flux of the Electric
Field LEAVING a surface is
 =  E  n out dA
Visualizing Flux
flux =  E  ndA = 
n is the OUTWARD
pointing unit normal.
Remember
flux =  E  ndA = 
E  n = E n cos( )
n

E
A
Component of E
perpendicular to
surface.
This is the flux
passing through
the surface and
n is the OUTWARD
pointing unit normal
vector!
Example
Cube in a UNIFORM Electric Field
Flux is EL2
E
Flux is -EL2
L
area
Note sign
E is parallel to four of the surfaces of the cube so the flux is zero across these
because E is perpendicular to A and the dot product is zero.
Total Flux leaving the cube is zero
Simple Example
1
r
q
 =  E  ndA =
dA
2

4e0 r
Sphere
1
q
q
=
2
4e0 r
1
q
 dA = 4e0 r 2 A
q
q
2
=
4r =
2
4e0 r
e0
1
Gauss’ Law
Flux is total EXITING the
Surface.
n is the OUTWARD
pointing unit normal.
qenclosed
 =  E  ndA =
e0
q is the total charge ENCLOSED
by the Gaussian Surface.
qenclosed
=
dA
E
n

e0
Line of Charge
Q
L
charge Q
=
=
length
L
Materials

Conductors






Electrons are free to move.
In equilibrium, all charges are a rest.
If they are at rest, they aren’t moving!
If they aren’t moving, there is no net force on them.
If there is no net force on them, the electric field must be
zero.
THE ELECTRIC FIELD INSIDE A
CONDUCTOR IS ZERO!
(23-6)
e
F
v
E
The electric field inside a conductor
We shall prove the the electric field inside a conductor vanishes
Consider the conductor shown in the figure to the left. It is an
experimental fact that such an object contains negatively charged
electrons which are free to move inside the conductor. Lets
assume for a moment that the electric field is not equal to zero.
In such a case an non-vanishing force F = eE is exerted by the
field on each electron. This force would result in a non-zero
velocity v and the moving electrons would constitute an electric
current. We will see in subserquent chapters that electric currents
manifest themselves in a variety of ways:
a) they heat the conductor
b) they generate magnetic fields around the concuctor
No such effects have ever been observed. Thus the original
assumption that there exists a non-zero electric field inside
the conductor. Thus we conclude that :
The electrostatic electric field E inside a conductor is equal to zero
Isolated Conductor
Electric Field is ZERO in
the interior of a conductor.
Gauss’ law on surface shown
Also says that the enclosed
Charge must be ZERO.
All charge on a
Conductor must reside on
The SURFACE.
Charged Conductors
Charge Must reside on
the SURFACE
-
E=0
-
-
s
Very SMALL Gaussian Surface
E
sA
EA =
e0
or
s
E=
e0
Charged Isolated Conductor




The ELECTRIC FIELD is normal to the
surface outside of the conductor.
s
The field is given by:
E=
e0
Inside of the isolated conductor, the Electric
field is ZERO.
If the electric field had a component parallel
to the surface, there would be a current
flow!!!
Isolated (Charged) Conductor with
a HOLE in it.
E
n
dA = 0 =
Q
e0
Because E=0 everywhere
inside the conductor.
There is no charge on the cavity walls. All the excess charge q
remains on the outer surface of the conductor
Symmetry: We say that an object is symmetric under a particular
mathematical operation (e.g. rotation, translation, …) if to an observer the
object looks the same before and after the operation.
Note:
Symmetry is a primitive notion and as such is very powerful
Rotational
symmetry
featureless
sphere
rotation
(23-10)axis
observer
Example of spherical symmetry
Consider a featureless beach ball
that can be rotated about a vertical
axis that passes through its center.
The observer closes his eyes and
we rotate the sphere. Then, when
the observer opens his eyes, he
cannot tell whether the sphere has
been rotated or not. We conclude
that the sphere has rotational
symmetry about the rotation axis.
Line of Charge
q
 E dA = e
n
0
h
E  2rh =
e0

E=
2e0 r
From SYMMETRY E is
Radial and Outward
Infinite Sheet of Charge
+s
h
E
cylinder
sA
EA + EA =
e0
s
E=
2e 0
We got this same
result from that
ugly integration!
E=
s
2e o
Electric field generated by a thin, infinite,
non - conducting uniformly charged sheet.
We assume that the sheet has a positive charge of
surface density s . From symmetry, the electric field
vector E is perpenducular to the sheet and has a
constant magnitude. Furthermore it points away from
the sheet. We choose a cylindrical Gaussian surface S
with the caps of area A on either side of the sheet as
shown in the figure. We devide S into three sections:
S1 is the cap to the right of the sheet. S2 is the curved
surface of the cylinder. S3 is the cap to the left of the
sheet. The net flux through S is  = 1 +  2 +  3
n̂2
S3
n̂3
1 =  2 = EA cos 0 = EA.  3 = 0
S2
n̂1
S1
( =90)
sA
  = 2 EA. From Gauss's law we have:  =
=
eo
eo
sA
s
 2 EA =
 E=
eo
2e o
(23-15)
qenc
Ei =
S
A
2s 1
eo
Eo = 0
A'
S'
The electric field generated by two parallel conducting infinite planes charged with
surface densities s 1 and -s 1. In fig.a and b we shown the two plates isolated so that
one does not influence the charge distribution of the other. The charge speads out
equally on both faces of each sheet. When the two plates are moved close to each
other as shown in fig.c, then the charges one one plate attract those on the other. As
a result the charges move on the inner faces of each plate. To find the field Ei between
the plates we apply Gauss' law for the cylindrical surface S which has caps of area A.
q
2s A
2s
The net flux  = Ei A = enc = 1  Ei = 1 To find the field Eo outside
eo
eo
eo
the plates we apply Gauss' law for the cylindrical surface S which has caps of area A.
q
s  s1
The net flux  = Eo A = enc = 1
= 0  Eo = 0
(23-16)
eo
eo
n̂2 Eo
The electric field generated by a spherical shell
of charge q and radius R.
Inside the shell : Consider a Gaussian surface S1
which is a sphere with radius r  R and whose
center coincides with that of the charge shell.
The electric field flux  = 4 r 2 Ei =
qenc
eo
=0
Thus Ei = 0
n̂1
Ei = 0
Eo =
q
4e o r 2
(23-17)
Ei
Outside the shell : Consider a Gaussian surface S2
which is a sphere with radius r  R and whose
center coincides with that of the charge shell.
q
q
The electric field flux  = 4 r 2 Eo = enc =
eo
Thus Eo =
eo
q
4e o r 2
Note : Outside the shell the electric field is the
same as if all the charge of the shell were
concentrated at the shell center.
Insulators





In an insulator all of the charge is bound.
None of the charge can move.
We can therefore have charge anywhere in
the volume and it can’t “flow” anywhere so it
stays there.
You can therefore have a charge density
inside an insulator.
You can also have an ELECTRIC FIELD in
an insulator as well.
Recipe for applying
Gauss’ Law
1. Make a sketch of the charge distribution
2. Identify the symmetry of the distribution and
its effect on the electric field
3. Gauss’ law is true for any closed surface S.
Choose one that makes the calculation of the
flux  as easy as possible.
4. Use Gauss’ law to determine the electric field
vector
qenc
=
eo
(23-13)
A uniformly charged cylinder.
rR
s
R
s
 (r 2 h)
E (2rh) =
e0
r
E=
2e 0
rR
 (R 2 h)
E (2rh) = =
e0
e0
q
R 2
E=
2e 0 r