Download Topic 6 - Interference

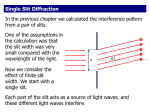
PHY 102: Waves & Quanta
Topic 6
Interference
John Cockburn (j.cockburn@... Room E15)
•Electromagnetic Waves
•Interference of Sound Waves
•Young’s double slit experiment
•Intensity distribution for Young’s experiment
Electromagnetic Radiation
•Visible light is an example of ELECTROMAGNETIC
RADIATION:
Electromagnetic Waves
•Existence predicted by James Clerk Maxwell (1865)
•Consist of “crossed” time-varying electric and
magnetic fields
•Transverse wave, both electric and magnetic fields
oscillate in a direction perpendicular to propagation
direction
•No medium is necessary: Electromagnetic waves can
propagate through a vacuum
•Constant speed of propagation through a vacuum:
c ≈ 3 x 108 ms-1
Electromagnetic Waves
Electromagnetic Waves
•It can be shown from MAXWELL’S EQUATIONS of
Electromagnetism (See second year course) that the
electric and magnetic fields obey the wave equations:
 Ey
2
x
2
 Ey
2
  0 0
t 2
 2 y( x, t ) 1  2 y( x, t )
 2
2
x
v
t 2
“standard” linear wave equation
 2 Bz
 2 Bz
  0 0
2
x
t 2
c
1
0 0
Electromagnetic Waves
E y  E0 sin( kx  t )
Bz  B0 sin( kx  t )
Where E0 and B0 are related by: E0 =
cB0
INTENSITY of an EM wave  E02
NB. we will see later that EM radiation sometimes behaves like a
stream of particles (Photons) rather than a wave………………
Speed of light in a material
•Constant speed of propagation through a vacuum:
c ≈ 3 x 108 ms-1
•But, when travelling through a material, light “slows
down”
c
v
n
n is the “refractive index” of the material.
Frequency of the radiation is constant, so from v = fλ, wavelength
must decrease by a factor of 1/n.
(NB refractive index depends on the wavelength of the light)
Interference
First, consider case for sound waves, emitted by 2 loudspeakers:
Path difference =nλ
Constructive Interference
Path difference =(n+1/2)λ
Destructive Interference
(n = any integer, m = odd integer)
Interference
Interference
For interference effects to be observed,
•sources must emit at a single frequency
•Sources must have the same phase OR have a FIXED phase difference
between them. This is known as COHERENCE
Conditions apply to interference effects for both light and sound
Example calculation
For what frequencies does constructive/destructive interference occur at P?
Young’s Double Slit Experiment
•Demonstrates wave nature of light
•Each slit S1 and S2 acts as a separate source of coherent light (like the
loudspeakers for sound waves)
Young’s Double Slit Experiment
Consider intensity distribution on screen as a function of  (angle measured
from central axis of apparatus)……………………….
If light behaves as a conventional wave, then we expect high intensity
(bright line) at a position on the screen for which r2-r1 = nλ
Expect zero intensity (dark line) at a position on the screen for which r2r1=(n+1/2)λ
Young’s Double Slit Experiment
Assuming (justifiably) that R>>d, then lines r2 and r1 are approximately
parallel, and path difference for the light from the 2 slits given by:
r2  r1  d sin 
Young’s Double Slit Experiment
Constructive interference:
d sin   n
Destructive interference:
1

d sin    n  
2

Young’s Double Slit Experiment
Y-position of bright fringe on screen: ym = Rtanm
Small , ie r1, r2 ≈ R, so tan ≈ sin
So, get bright fringe when:
n
ym  R
d
(small  only)
Young’s Double Slit Experiment:
Intensity Distribution
For some general point P, the 2
arriving waves will have a path
difference which is some
fraction of a wavelength.
This corresponds to a difference
 in the phases of the electric
field oscillations arriving at P:
E1  E0 sin t 
E2  E0 sin t   
Young’s Double Slit Experiment:
Intensity Distribution
Total Electric field at point P:
ETOT  E1  E2  E0 sin t   E0 sin t   
Trig. Identity:
1
 1

sin   sin   2 cos      sin     
2
 2

With  = (t + ), = t, get:


ETOT  2 E0 cos  sin t   
2



ETOT  2 E0 cos  sin t   
2



2
E
cos
So, ETOT has an “oscillating” amplitude:  0
2 

Since intensity is proportional to amplitude squared:
 
2
I TOT  4 E0 cos 2  
2
Or, since I0E02, and proportionality constant the same in both cases:
 
I TOT  4 I 0 cos 2  
2
phase difference
path difference

2


d sin 

2

 
I TOT  4 I 0 cos 2  
2
I TOT
 d sin  
 4 I 0 cos 

  
2
For the case where y<<R, sin ≈ y/R:
 dy 
I TOT  4 I 0 cos 2 

R



Young’s Double Slit Experiment:
Intensity Distribution
I TOT
 dy 
 I 0 cos 

 R 

2