* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Nanostructured Carbon Allotropes as Weyl
Canonical quantum gravity wikipedia , lookup
Technicolor (physics) wikipedia , lookup
Topological quantum field theory wikipedia , lookup
An Exceptionally Simple Theory of Everything wikipedia , lookup
Future Circular Collider wikipedia , lookup
Quantum chromodynamics wikipedia , lookup
Renormalization group wikipedia , lookup
Canonical quantization wikipedia , lookup
Elementary particle wikipedia , lookup
Event symmetry wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
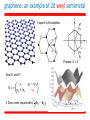
History of quantum field theory wikipedia , lookup
Identical particles wikipedia , lookup
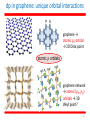
Relativistic quantum mechanics wikipedia , lookup
Dirac equation wikipedia , lookup
Mathematical formulation of the Standard Model wikipedia , lookup
Standard Model wikipedia , lookup
Nanostructured Carbon Allotropes as Weyl-Like Semimetals Shengbai Zhang Department of Physics, Applied Physics & Astronomy Rensselaer Polytechnic Institute symmetry In quantum mechanics, symmetry can be critically important. Consider, for example, a two-particle system. Under particle exchange, bosons satisfy 𝜓 𝑟1 , 𝑟2 = 𝜓 𝑟2 , 𝑟1 , whereas fermions satisfy 𝜓 𝑟1 , 𝑟2 = −𝜓 𝑟2 , 𝑟1 . Just because the symmetry, bosons and fermions are very different from classical particles. Recent development in solid-state physics is also about symmetry: in case of Weyl fermions, chiral symmetry leads to novel properties/topological protection not envisioned before. 2 topological protection a normal ring One cannot deform a normal ring into a Mobius ring without cutting the strip and a Mobius ring then rejoin. 3 solid and its bloch wave A solid is a periodic system in which electron wavefunction may be written as a Bloch wave 𝜓𝑘 𝑟 = 𝑒 𝑖𝑘∙𝑟 𝑢𝑘 𝑟 = 𝑒 𝑖𝑘∙𝑟 𝑢 𝑘 . The reciprocal space of 𝑟 is the 𝑘 space in which the smallest repeating unit defines the Brillouin zone. Brillouin zone (BZ) forms a closed loop in the sense that a 𝑘-point exiting from one face of the BZ is equivalent to reentering from the opposite face of the BZ. 4 berry curvature & chiral quantum number Electron living inside the Brillouin zone feels an (effective) vector potential 𝐴 𝑘 = 𝑖 𝑢 𝑘 𝛻𝑘 𝑢 𝑘 (Berry connection). The corresponding (Berry) curvature 𝐹 𝑘 = 𝛻𝑘 × 𝐴 𝑘 defines a field (similar to a magnetic field 𝐵). Chiral quantum number is defined by χ = 1 𝐹 2𝜋 𝐹𝑆 𝑘 ∙ 𝑑 𝑆𝑘 (Chern number). Non-trivial Chern number (+1 or −1) tells the chirality (righthanded or left-handed). 5 low-energy particles Tomorrow's condensed matter physics will be rooted in many- body physics – studying collective excitations and quasiparticles Theory developed for elementary particles can be shipped here to explore many-body interactions which cannot be easily obtained from experiment via serendipity. → Theory is and will lead the way. Compared to traditional particle physics, condensed matter is a much richer field and experimental test should be easier. → An emerging battlefield of particle physics. Good condensed matter physicist needs to be intradisplinary! 6 spin-half dirac fermions Dirac Hamiltonian (3D): 𝑚𝑣 2 𝐻= 𝑣𝜎 ∙ 𝑝 𝑣𝜎 ∙ 𝑝 = −𝑚𝑣 2 𝑚𝑣 2 0 0 𝑚𝑣 2 𝑣𝑝𝑧 𝑣 𝑝𝑥 − 𝑖𝑝𝑦 𝑣 𝑝𝑥 + 𝑖𝑝𝑦 −𝑣𝑝𝑧 Massless Dirac fermions (𝑚 = 0), 𝐻 = 0 𝑣𝜎 ∙ 𝑝 𝑣𝑝𝑧 𝑣 𝑝𝑥 − 𝑖𝑝𝑦 𝑣 𝑝𝑥 + 𝑖𝑝𝑦 −𝑣𝑝𝑧 −𝑚𝑣 2 0 0 −𝑚𝑣 2 𝑣𝜎 ∙ 𝑝 0 Dirac semimetal (4x4 matrix; doublydegenerate Dirac cones; linear (2-Dirac points) dispersion in all three directions). M. Koshino 7 3-dimensional spin-half weyl fermions NJP 9, 356 (2007) Separate in kspace the two Dirac cones : Now, each cone is described by a 2x2 Weyl Hamiltonian: 𝐻± = 𝑝𝑧 ±𝑣 𝑝𝑥 + 𝑖𝑝𝑦 𝑝𝑥 − 𝑖𝑝𝑦 . Weyl fermions are protected by the chiral −𝑝𝑧 symmetry discussed earlier, so they are robust against perturbations. 8 surface states: fermi arcs Weyl points of different chirality's can be viewed as magnetic monopoles (MMP) with ±charges On the surfaces of a slab, Fermi arcs appear, which is characteristic of Weyl semimetal. y A state moving in the (+y)-direction on top surface cannot be scattered back. To observe Weyl points, the material must do not have either time reversal symmetry or inversion symmetry. 9 why bother? Weyl semimetal exhibits chiral anomaly, meaning chiral “charges” are not conserved. One can use 𝐵 ∥ 𝐸 fields to pump charge from one chiral channel to another. Experimental ramifications include negative magnetoresistance; quantum anomalous Hall effect (for dissipationless carrier transport like superconductivity); non-local transport; and non-conservation of ordinary current (at least locally). It can also give rise to unusual optical conductivity, and many more. real-part of optical conductivity 𝜎𝑥𝑥 versus chemical potential 𝜇 & optical frequency 𝜔. 10 dirac/weyl semimetal as an intermediate phase A Dirac or Weyl semimetal is an intermediate phase in the transition between a topological insulator (TI) phase and a normal insulator (NI) phase. Topological insulator are materials with large spin-orbit coupling (SOC), such as Bi2Te3 Search for Weyl semimetals also follows the same line of thought. 11 in pursuit of weyl semimetal (current status ) Photonic crystal: Science 349, 622 (2015) 30-meV gap TaAs (Ta is heavy, large spin-orbit coupling): Science 349, 613 (2015); PRX 5, 031013 (2015). TaAs Band Structure (E versus k) (eV) Drawbacks with TaAs: Too many Weyl points (24 in total) and they are too close (only ~% of BZ), unlike graphene Trivial Fermi pockets at Fermi level dominate (zero gap in the DOS). 12 what might be the next? discovery of Weyl semimetal is an APS Highlight of the Year You bet, the study of Weyl fermion will continue # papers with “Weyl” in topic Regardless, experimental # papers with “graphene” in topic: 1945-2016 0 (1945-1990); 95,366 (1991-2016); 1,803 (2016 alone); >100 per day now. 13 graphene: an example of 2d dirac weyl semimetal 𝑟-space: A,B sublattice 𝑘-space: 𝐾 ≠ 𝐾′ Near 𝐾 and 𝐾’: 𝑝0𝑧 𝐻=𝑣 𝑝𝑥 + 𝑖𝑝𝑦 𝑝𝑥 − 𝑖𝑝𝑦 −𝑝 0𝑧 2 Dirac cones separated by 1 3 𝒃𝟏 − 𝒃𝟐 . K’ K 14 carbon allotropes Graphene Graphite + many more … Carbon has many allotropes due to its exceptionally strong C-C bonds. Once formed, these allotropes are hard to break. Carbon nanotube C60 15 dp in graphene: unique orbital interactions 𝑝𝑧 𝑝𝑧 graphene → atomic 𝑝𝑧 -orbital → 2D Dirac point atomic 𝑝 orbitals 𝑝𝑦 𝑝𝑥 graphene network → atomic (𝑝𝑥 , 𝑝𝑦 )orbitals → 3D Weyl point? 16 so, here is our charge Search for systems whose orbital interactions have the form of 3D Weyl Hamiltonian However, different from others searching for existing materials of limited use and supply, we target materials of broad use but in forms not yet synthesized In the process, we also uncovered structures with Hamiltonians that do not fit into any of the currently known models. 17 why weyl-like semimetal? Light elements have exceedingly small spin-orbit coupling (SOC for carbon ~1 millikelvin) At room temperature, (thermal scattering)/SOC is 300𝐾/0.001𝐾 = 3 × 105 Hence, for most applications, spin may be treated as a dummy variable, leading to Weyl-like semimetals Conclusion: Weyl physics exists in solids made of purely light elements (the lighter, the better). 18 interpenetrated graphene network (IGN) 𝑠𝑝3 𝑠𝑝2 Formation energy (eV/C) Graphene Diamond IGN C60 0.0 0.13 0.23 0.37 No imaginary-frequency phonons → kinetically stable. 19 weyl line nodes Brillouin zone 𝜃 Z T G Y Weyl wedge 𝐸𝐹 Line nodes are the only Fermi surface for the entire system, along which the energy dispersion looks like a wedge. Nano Letters 15, 6974 (2015) 20 emergence of weyl points One may break the inversion symmetry either (1) by displacing some carbon atoms or (2) by inserting He interstitials, both turn the Weyl line nodes into points (1) (2) 21 fermi arcs appear on the [010] surface Schematic Nano Letters 15, 6974 (2015) Actual calculation 22 back to line nodes: what is unique? Chern number: χ = 1 2𝜋 𝐴 𝑘 ∙ 𝑑 𝑙𝑘 Co-dimension = 2 (even) → weaker but non-vanishing topological protection. Line node gives rise to topologicallyprotected flat bands on surfaces. On PRB 82, 184502 (2010) a flat band, Coulomb repulsion U is exceptionally large, leading to a strong electron-electron correlation Can you imaging strongly-correlated carbon? 23 line nodes are robust under uniaxial strain 𝜃 → reducing 𝜃 Topological protection remains until a critical angle 𝜃 = 64°. 24 at 𝜃 = 64° transition from IGN to CKL Interpenetrated graphene network (IGN) 1/3 C 4fold; 2/3 C 3fold (sp2) Nano Letters 15, 6974 (2015) Carbon Kagome lattice (CKL) G-3 All C 4fold (sp3) PRL113, 085501 (2014) 25 understanding electronic properties Polyacetylene is the root for most carbon allotropes. By connecting the chains, one builds graphene, 𝐸𝐹 diamond, IGN, anti-bonding state Kagome lattice, etc. G Different A(=Z) characters of the occupied and empty states are the reason for bonding state Weyl semimetal. 26 band inversion yields topological protection Increasing uniaxial strain 1D→3D IGN CKL polyacetylene 𝐸𝐹 A G Red = 1 Blue = 2 Green = 3 27 ckl is as remarkable as ign 3.4-eV direct gap (blue color) (by HSE calc.) Effective mass 𝑚∗ ’s comparable to Si Light absorption comparable to GaN Realization of optical-electronic integration in one material. Phys. Rev. Lett. 113, 085501 (2014) 28 frustration in triangular lattice 𝑝-orbital carbon Kagome lattice Frustration in life + − 𝑝-down 𝑝-up Frustration in physics Upon doping, will carriers in CKL act as spin-like liquid? 29 there is a whole family of 3d-graphene weyl semimetals 2-type carbon rings (more stable than IGN) Weyl surface nodes as Fermi level Co-dimension = 1 (odd) → more topological protection (?) Colors denote different types of carbon 30 ordered random (b) (a) Transmission Electron Microscopy (TEM) images of carbon channels. Most of the channels are perpendicular to the page. Featured in Physics & Editor’s Suggestion 31 summary Weyl-line nodes in interpenetrated carbon network [Nano Letters 15, 6974 (2015)] Carbon Kagome lattice [Phys Rev Lett 113, 085501 (2014)] Weyl-surface nodes in three-dimensional graphene [under review by Nanoscale (2016)] 32 acknowledgements Vincent Meunier Marvin Cohen, UCB Yuanping Chen Yiyang Sun Han Wang Damien West Rensselaer Polytechnic Institute S.Y. Yang, Singapore Fan Zhang, UT Dallas 33