Download Quantum Magnetic Dipoles and Angular Momenta in SI Units

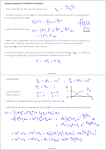
Quantum Magnetic Dipoles and Angular Momenta in SI Units
Bohr Magneton
It seems to be agreed upon that in SI units, we define the Bohr magneton µB and the nuclear
magneton µp by
e~
µB ≡
2m
e~
µp ≡
2mp
where e is the proton charge (and the negative of the electron charge), m is the electron mass, and
mp is the proton mass (or also possibly the neutron mass, according to Abers’ [1] notation). So a
“magneton” has the same dimension as magnetic dipole moment (µ).
See, for example, [ http://physics.nist.gov/cgi-bin/cuu/Value?eqmun ] for verification.
Relation of Magnetic Dipole Moment to the Magneton
We derive the electron’s orbital magnetic dipole moment µ and find the motivation for the definition
of the Bohr magneton.
Using the assumptions of Bohr’s atomic model, the electron circulates in a flat orbit of radius r,
with angular momentum L = |r × p| = mrv, and
evr
v e
e
(πr2 ) = −
µ = IA = −e
=−
mvr = −
L
2πr
2
2m
2m
p
Since we may have L = ~ l(l + 1), this becomes
p
e~ p
l(l + 1) ≡ µB l(l + 1)
µ=−
2m
so we see how the orbital magnetic dipole moment of the electron is quantized in terms of µB . (So
a magneton is a quantum of magnetic dipole moment.)
Note that when we include spin, we get
e
e
µB
µB
µ=−
L−g
S =− L−g
S
(1)
2m
2m
~
~
Angular Momentum Operator Definitions and Conventions
Now, in quantum mechanics we have the freedom to define the angular momentum operators (Ĵ, L̂,
and Ŝ) and the magnetic dipole moment operator (µ̂) using different conventions: we may define
them to have the same dimension as angular momentum and magnetic dipole moment, respectively,
or we may define them to be dimensionless. Taking the operator Ĵ for example, we may have
p
Ĵ ≡ r̂ × p̂ so that J = ~ j(j + 1)
when it acts on angular momentum eigenstates, or we may have
p
~Ĵ ≡ r̂ × p̂ so that J = j(j + 1)
when it acts on angular momentum eigenstates. The table below summarizes these options and the
resulting consequences for equation 1 above.
Possible Conventions
Resulting Equation
Ĵ, L̂, Ŝ “dimensionful”
µ̂ “dimensionful”
µ̂ = − µ~B L̂ − g µ~B Ŝ
Ĵ, L̂, Ŝ “dimensionful”
µ̂ dimensionless
µ̂ = − ~1 L̂ − g ~1 Ŝ
Ĵ, L̂, Ŝ dimensionless
µ̂ “dimensionful”
µ̂ = −µB L̂ − gµB Ŝ
Ĵ, L̂, Ŝ dimensionless
µ̂ dimensionless
µ̂ = −L̂ − g Ŝ
1
References
[1] Ernest S. Abers: Quantum Mechanics, Pearson, Prentice Hall (2004)
2