Download Biomedical Imaging and Applied Optics Laboratory

Biomedical Imaging and Applied Optics Laboratory Department of Electrical and Computer Engineering - University of Cyprus Spectral Analysis of Optical Coherence Tomography Signals by Andreas Kartakoullis Submitted to the University of Cyprus in partial fulfillment of the requirements for the degree of Master of Science in Electrical Engineering Department of Electrical and Computer Engineering May 2008 SPECTRAL ANALYSIS OF OPTICAL COHERENCE TOMOGRAPHY SIGNALS By Andreas Kartakoullis Submitted to the University of Cyprus in partial fulfillment of the requirements for the degree of Master of Science in Electrical Engineering Department of Electrical and Computer Engineering May 2008 SPECTRAL ANALYSIS OF OPTICAL COHERENCE TOMOGRAPHY SIGNALS By Andreas Kartakoullis Examination committee: Dr. Constantinos Pitris Assistant Professor, Department of ECE, Research Supervisor Dr. Stavros Iezekiel Associate Professor, Department of ECE, Committee Member Dr. Michalis Averkiou Assistant Professor, Department of MME, Committee Member Abstract More than 85% of all cancers originate in the epithelium that lines the internal surfaces of organs throughout the body. Before they become invasive, at stages known as dysplasia and carcinoma in situ, early cancer cells alter the epithelial-cell architecture. More specifically, the number of cells, and therefore the number of nuclei, increases. The nuclei themselves become enlarged and hyperchromatic, i.e. their chromatin changes and colours more darkly when stained during histopathology. Nuclear sizes change from the normal 5 − 10 µm to 1.5 − −2 x the size, i.e. 10 − 20 µm. Currently, these early changes are only detectable by histopathology or, non-invasively, by optical imaging techniques such as confocal or multi-photon microscopy. Unfortunately, neither of the two techniques has been clinically implemented due their complexity and their limited penetration in tissue. Optical Coherence Tomography (OCT) is a prominent non-invasive biomedical tissue imaging technique that generates in vivo cross-sectional images of tissue microstructure with micron-scale spatial resolution. OCT can overcome the limitations of the other techniques; but the dysplastic alterations are not clearly discernible even for the resolution of OCT. However, it is well known that changes in scatterer size induce changes in the spectral content of scattered light. These changes have been found to be diagnostically useful in scattering spectroscopy in the visible range. Cellular organelles in epithelial tissue can be modelled as spheroidal scatterers whose interactions with light are governed by Mie theory. Mie theory provides an analytical closed-form description of optical scattering from single spheroidal particles as a function of particle size, refractive index, wavelength, observation angle, and optical polarization. This type of analysis can be applied to OCT to enable the detection of the early changes of dysplasia. Spectroscopic OCT (SOCT) is the spectroscopic extension of OCT and it can enhance the contrast of OCT systems by differentiating tissue based on properties other than the intensity of the backscattered light, such as different spectral features of the detected spectrum at each pixel in the image. Currently two approaches for sizing the scatterers based on the measured spectra, the first approach is based on curve fitting the normalized experimental measurement to the theoretical Mie prediction. The second approach is based on pitch detection such as using the Fourier transform or determining the autocorrelation. We have exploited the stochastic nature of the OCT signal due to speckle, since multiple scatterers coexists in the OCT imaging volume causing the backscattered fields to interfere coherently with one another in a stochastic process. The detected spectrum therefore is an outcome of that stochastic process, where the statistical properties are determined by the scatterers size and concentration. By analyzing the statistical properties of the backscattered spectra, information about the underii lying distribution of scattering particles can be extracted and speckle can be used as a diagnostic tool. This thesis introduces a novel method for scatterer size estimation and classification using SOCT based on autoregressive spectral estimation techniques and statistical analysis. Principal Component Analysis (PCA) based algorithm was used to extract diagnostic features and to reduce the dimension of the spectra. The extracted features of each sample are then input into a classification process using Multivariate Analysis of Variance (MANOVA), and to give solution to the size equations. The results are very encouraging and indicate that the spectral content of OCT signals can be used to estimate scatterer size and classified with high accuracy. This technique can result in an extremely valuable tool for the investigation of disease tissue features which now remain below the resolution of OCT. iii PerÐlhyh Ta j lio perissìtera pou eÐdh kalÔptei tic karkÐnou, perissìtero eswterÐkec epifniec apo twn 85% , proèrqontai orgnwn se ìlo apì to to epi- s¸ma. Ta prwÐma karkÐnika stdia, eÐnai gn¸sta wc dusplsia kai karkÐnwma in-situ, ìpou sta stdia aut sunteloÔntai sugkekrimèna, oi pur nec. pur na ta qarakthrÐs tikec epijhlÐaka EpÐshc oi alloÐ¸netai kÔttara pur nec apì alloÐwseic auxnontai diogkìnwntai kai me sta epijhlika apotèlesma na 10 − 20 µm se . Pio auxnontai uperqrwmatÐzontai, 5 − 10 µm 1.5 − −2 x kÔttara. to mègejoc Mèqri kai tou s tigm c h dignwsh twn neoplasi¸n basÐzetai se is tologikèc exetseic twn is t¸n apì bioyÐec kai ektomèc. Oi monèc mh-epembatikèc teqnikèc pou èqoun aut thn dunatìthta di- gnwshc den èqoun brei klinik efarmog lìgw problhmtwn me thn axiopis tÐa touc kai me H Ð na thn praktik efarmog touc. Optik SÔmfwnh xepersei autèc (∼ 2 − 3 mm) kai TomografÐa tic (Optical adunamÐec. eukrÐneia thc çherence MporeÐ txewc na Tomography petÔqei OCT), ikanopoihtik (1 − 15 µm) mikromètrwn , mpore- dieÐsdush ìmwc oi dusplas tikèc alloi¸seic den eÐnai pl rwc eudikritec akìma kai me thn eukrÐneia aut . Oi dusplas tikèc toskopik¸n allagèc (Light teqnik¸n, sto Ektetamènh alloi¸seic mègejoc ereun Scattering gnws tik tìte afoÔ tou èqei ìpwc gÐnei Ean to ta ìmwc eÐnai skedas t sthn Spectroscopy qr simh. skedas tèc, mporoÔn na diagnws toÔn gnws tì apì dhmiourgoÔn perioq LSS) epijhliak thc pou opisjoskedasmèno fsma thn sto aut h Optik c mia jewrÐa, san sunis t¸sa fsma. Skèdashc prosèggish montelopoihjoÔn perièqei fasma- skedasmèno FasmatoskopÐac ìti qr sh hlektromagnhtik metabolèc èdeixe kÔttara thn me eÐnai dia- sfairikoÐ Mie pou exarttai apì to mègejoc, thn sugkèntrwsh kai to deÐkth dijlashc twn skedas t¸n. Ta qarakthris tik aut mporeÐ na prosdioris toÔn me duo trìpouc, me thn qr sh thc jewrÐac Mie opoÔ ta peiramatik apotelèsmata prosarmìzontai sta jewrhtik [5]. O deÔte- roc trìpoc eÐnai me ton entopismì apotìmwn ektinxewn, panw apì èna kat¸fli, thc autosusqètishc kurÐwc thc tou qr sewc fsmatoc. fak¸n me 'Omwc qamhlì h LSS èqei noigma arketèc èmfutec diafrgmatoc (NA), adunamÐec pou èqei lìgw san a- potèlesma qamhl egkrsia eukrÐneia kai periorismènh dieÐsdush lìgw exasjènhshc. An kai èqei prosarmos teÐ sthn LSS sumbolometrÐa qamhl c sumfwnÐac gia skopoÔc beltÐwshc thc 'Ena fwc gia rioqèc anlushc den sumbatikì na me sÔs thma dhmiourg sei parìmoia eÐnai teqnik OCT qrhsimopoieÐ dusdis tatec èntash den apeikìnishc all leitourgik teqnik . mporoÔn thn èntash eikìnec diatom c na pl rwc eÐnai tou tou opisjoskedasmènou deÐgmatoc. eudikritec stic 'Omwc pe- sumbatikèc eikìnec OCT epÐshc swreÐa plhrofori¸n pou perièqetai se llec paramètrouc ektìc apì thn èntash den axiopoieÐtai. Mia prìsfath fasmatoskopik proèktash thc OCT eÐnai fasmatoskopik h SOCT pou opisjoskedasmèno epitrèpei fwc, se thn epÐshc dusdis tatec v exagwg qarakthris tik¸n apeikonÐseic. Ston apì to apeikonis tikì q¸ro tou OCT sunuprqoun tautìqrona pollaploÐ skedas tèc pou lìgw thc optik c sumfwnÐac s tigm c san thn h tou s matoc kìkkwsh s toqas tik Aut èntash mia tou OCT ta idiìthtec kai s matoc tou pou mporoÔn eÐnai tìso dhmiourgoÔn wc pou phg eÐnai katanom s toqas tik eikìna OCT jewreÐtai diergasÐa sugkèntrwsh OCT. thc twn motÐba kai apotèlesma jorÔbou èqei skedas t¸n mèsa sthn thc ston SOCT mporoÔme na qrhsimopoihjoÔn gia upologismì kìkkwshc. Mèqri apeikìnish. 'Omwc exart¸ntai apì to apeikonis tikì parousizontai fsma. s toqas tik c fsmatoc motÐba bioiatrik pou opisjoskedasmèno aut c opisjoskedasmènou sthn idiìthtec kìkkwshc sto s toqas tik 'Etsi, diadikasÐac, na exgoume mègejoc, q¸ro tìso thc sthn jewr¸ntac ìti melet¸ntac tic qarakthris tik megèjouc tou skedas t . AnalÔontac tic s tatis tikèc idiìthtec tou opisjoskedasmènou optikoÔ fsmatoc me thn qr sh plhroforÐec prohgmènwn sqetik me mejìdwn thn trìpo se pragmatikì qrìno. anlushc morfologÐa kai mporoÔme sÔnjesh na tou anakt soume is toÔ me mh- polÔtimec epembatikì Pio sugkekrimèna qrhsimopoÐhjhke èna autopalindromi- kì montèlo fasmatoskopik c ektÐmhshc basismèno sthn mèjodo Burg gia thn ankth- sh tou opisjoskedasmènou (Principal jhke gia çmponentc exagwg kai thn uprqoun twn apotelesmtwn Ta tou 'Epeita anlush twn opisjoskedasmènou pou ja mac prwteÔwn fsmatoc odhg soun ston sunis tws¸n pragmatopoÐh- upologismì tou Me thn qr sh PCA petuqaÐnoume thn meÐwsh tou megèjouc twn epanadom sh pou mejìdou. na Analysic) qarakthris tik¸n megèjouc skedas t . dedomènwn fsmatoc. touc anagnwrÐzontai katadeÐxe apotelèsmata thn thc me arket tètoio pio eÔkola. euaisjhsÐa mejìdou pou trìpo kai thn ¸ste ta diaforetik AkoloÔjwc eidikìthta anaptÔqjhke eÐnai prìtupa kathgoriopoÐhsh thc proteinomènhc arkèta enjaruntik gia peraitèrw melèth ètsi ¸ste na axiopoÐhjei san èna qr simo ergaleÐo gia dignwsh pajologÐwn pou paramènoun ktw apì thn eukrÐneia twn sus t matwn OCT. vi Contents 1 Introduction 12 1-1 Optical Coherence Tomography as a Biomedical Imaging Technology 12 1-2 Spectroscopic Optical Coherence Tomography . . . . . . . . . . . . 13 1-3 Scope of the Thesis . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 2 Optical Coherence Tomography 2-1 Introduction . . . . . . . . . . . . . . . . . . . . 2-2 Time-Domain OCT (TD-OCT) . . . . . . . . . 2-2.1 Interferometer with Coherent Light . . . 2-2.2 Interferometer with Low Coherence Light 2-2.3 Nondispersive Medium . . . . . . . . . . 2-2.4 OCT Resolution . . . . . . . . . . . . . . 2-2.5 Group Velocity Dispersion . . . . . . . . 2-3 Optical Sources . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 Mie Theory 3-1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . 3-2 General Formulation of the Problem . . . . . . . . . . . 3-2.1 Boundary Conditions . . . . . . . . . . . . . . . . 3-2.2 Solutions to the vector wave equations . . . . . . 3-3 Expansion of a plane wave in vector spherical harmonics 3-4 The internal and scattered fields . . . . . . . . . . . . . . 3-4.1 Angle-Dependent Functions . . . . . . . . . . . . 3-4.2 Scattering Coefficients . . . . . . . . . . . . . . . 3-5 Scattering Matrix . . . . . . . . . . . . . . . . . . . . . . 3-6 Computation of Scattering Coefficients . . . . . . . . . . 3-7 Mie Theory for Biomedical Optics . . . . . . . . . . . . . 4 Spectroscopic OCT 4-1 Introduction . . . . . . . . . . . . . . . 4-2 Mie theory in SOCT . . . . . . . . . . 4-3 Speckle . . . . . . . . . . . . . . . . . . 4-4 SOCT Instrumentation . . . . . . . . . 4-4.1 Superluminescent diodes (SLDs) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 15 16 16 19 20 21 22 23 . . . . . . . . . . . 27 27 27 29 30 36 37 39 40 42 44 45 . . . . . 46 46 47 47 49 49 CONTENTS 8 4-5 Tissue Phantoms . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 Spectral Analysis of OCT Signals 5-1 Introduction . . . . . . . . . . . . . . . . . . . . . . . 5-2 Spectral Analysis Based on Fourier Transformation . 5-2.1 Energy Spectrum Density (ESD) . . . . . . . 5-2.2 Power Spectrum Density (PSD) . . . . . . . . 5-2.3 Computation using the FFT . . . . . . . . . . 5-3 Spectral Analysis Based on Burg’s Method . . . . . . 5-3.1 Rational Power Spectra . . . . . . . . . . . . 5-3.2 Burg’s Method . . . . . . . . . . . . . . . . . 5-4 Statistical Multivariate Analysis . . . . . . . . . . . . 5-4.1 Principal Component Analysis (PCA) . . . . . 5-4.2 Multivariate Analysis of Variance (MANOVA) 5-4.3 Classification . . . . . . . . . . . . . . . . . . 50 . . . . . . . . . . . . 53 53 54 54 55 56 57 57 58 60 60 62 62 . . . . 63 63 63 66 71 7 Summary and Future Work 7-1 Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7-2 Future Work . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75 75 75 Bibliography 77 6 Results 6-1 Introduction . . . . 6-2 Spectra Calculation 6-3 Spectral Analysis . 6-4 Depth Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . List of Figures 1.1 Growth of OCT scientific and medical research publications. The graph shows the number of publications per year with optical coherence tomography in the title as indexed in the PubMed and Citation databases [8]. . . . . . . . . . . . . . . . . . . . . . . . . 13 Schematic of Time Domain OCT system with a moving mirror in the reference arm. . . . . . . . . . . . . . . . . . . . . . . . . . . . 16 2.2 The Michelson interferometer. . . . . . . . . . . . . . . . . . . . . 17 2.3 Interferometric pattern resulting from moving the reference arm and using a coherent source. Interferometric pattern resulting from moving the reference arm and using a low coherence source. . . . . 19 Spectral absorption of some tissue molecules, and of aortic tissue. The brightened wavelength ranges have already been used in OCT [30]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24 The incident field (Ei ,Hi ) gives rise to a field (E1 ,H1 ) inside the particle and a scattered field (Es ,Hs ) in the medium surrounding the particle. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 3.2 Closed surface separating regions 1 and 2. . . . . . . . . . . . . . 30 3.3 Scattering by a spherical particle . . . . . . . . . . . . . . . . . . 32 3.4 Polar plots of the first five angle-dependent functions πn (a) and τn (b) (n = 1, . . . , 5). All functions are plotted to the same scale. . . 41 Example of back-scattered intensity. (a) Back-scattered intensity for 1 µm scatterer. (b) Back-scattered intensity for 2 µm scatterer. (c) Back-scattered intensity for 4 µm scatterer. . . . . . . . . . . . 48 4.2 Schematic of the Time Domain OCT system that we used. . . . . 50 4.3 OCT image of a piece of the phantom placed on an unpolished metal substrate. The two vertical bars represent z, z 0 , from top to bottom. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52 2.1 2.4 3.1 4.1 6.1 The autocorrelation of the backscattering spectra obtained with FFT 65 LIST OF FIGURES 6.2 6.3 6.4 6.5 10 Back-scattered normalized average power spectra obtained with Burg’s method . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65 Plots of mean error and sensitivity versus N Burg (a), (c) and principal components (b), (d) for Burg’s method . . . . . . . . . . . . 69 Plots of mean error and sensitivity versus N F F T (a), (c) and principal components (b), (d) for FFT/Autocorrelation . . . . . . . . . 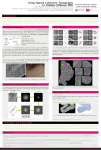69 Results of the MANOVA analysis of 100 training and 100 sample spectra for the single power (a), the single power and the derivative (b), the single and square power (c). (The dark lines are the classification area borders resulting from the discriminant analysis) 70 6.6 Spectra from different depths with the focus at the top of the sample 72 6.7 Spectra from different depths with the focus at the middle of the sample . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72 Spectra from different depths with the focus at the bottom of the sample . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73 6.9 Spectra from below the surface at different pathlengths . . . . . . 73 6.10 Spectra from the same depth from three different OCT images . . 74 6.11 In focus spectra from three different OCT images . . . . . . . . . 74 6.8 List of Tables 2.1 Short coherent sources suitable for use in OCT systems [34] . . . . 25 4.1 Recipes for tissue phantoms (acrylamide gel) of different imaging volume concentration . . . . . . . . . . . . . . . . . . . . . . . . . 51 6.1 6.2 6.3 6.4 6.5 6.6 Results for Burg’s Method with window 3001 x 25 pixels and p = 120 AR parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Results for FFT/Autocorrelation with window 3001 x 25 pixels and N F F T = 212 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Results for square power of the spectrum P̂Bu . . . . . . . . . . . . tr Bu ˆ tr . . . . . . . . . . . . . Results for derivative of the spectrum dP . . . . . . . . . . . . Results for single power and derivative of P̂Bu tr . . . . . . . . . . Results for single power and square power of P̂Bu tr 68 68 68 68 68 68 Chapter 1 Introduction 1-1 Optical Coherence Tomography as a Biomedical Imaging Technology In the last 40 years, many tomographic imaging modalities have been developed such as Computed Tomography (CT), Magnetic Resonance Imaging (MRI), Ultrasound (US), and Positron Emission Tomography (PET). Optical coherence tomography (OCT) is a relatively recent imaging technology for producing high-resolution cross-sectional images [1]. OCT plays an important role in biomedical imaging due to its micrometer resolution and millimeter penetration depth. If different biomedical imaging technologies are classified by their applicable size scales, which vary from whole body imaging, organ imaging, tissue imaging, and cellular imaging down to molecular imaging, OCT currently represents one the finest resolutions among in vivo tomographic imaging modalities. Optical Coherence Tomography (OCT) is analogous to ultrasound imaging but is based on the detection of infrared light waves, instead of sound, back-scattered (reflected) from different layers and structures within the tissue. Typically, a fiber optic Michelson interferometer is used to measure the relative optical path difference between a reference arm and the various layers of the tissue sample in the sample arm. By mechanically varying the path length in the reference arm with a scanning galvanometer an interference fringe is obtained for an arbitrary path length in the sample. To generate a single Axial scan (A-scan) in the image, an optical beam is incident on the sample at a single transverse location while the reference arm is scanned. The field of OCT has evolved rapidly in the past years years (Figure 1-1 encompassing many clinical applications. A major step in clinical implementation was the achievement of high speed imaging capabilities by using Fourier domain detection techniques, such as Fourier-Domain OCT (FD-OCT) and Swept-Source OCT 1-2 Spectroscopic Optical Coherence Tomography 13 (SS-OCT). OCT has made its most significant clinical contribution in the field of ophthalmology, where it has become a key diagnostic technology in the areas of retinal diseases and glaucoma [2]. Also, OCT has been extensively applied in the field of cardiology, to examine the structural integrity of the vasculature in the coronary arteries [3, 4]. More recently it has been applied for cellular and molecular analysis using modalities such as Spectroscopic OCT [5, 6] and Polarization-Sensitive OCT (PS-OCT) [7]. When fully exploited, OCT has the potential to dramatically change the way physicians, researchers and scientists see and understand human tissues in order to better diagnose and treat disease. Figure 1.1: Growth of OCT scientific and medical research publications. The graph shows the number of publications per year with optical coherence tomography in the title as indexed in the PubMed and Citation databases [8]. 1-2 Spectroscopic Optical Coherence Tomography An extension of OCT is Spectroscopic OCT (SOCT) for performing both crosssectional tomographic imaging of the structure and imaging of the spectral content. SOCT is able to perform depth-resolved spectroscopy, offering the possibility of reconstructing 3-d spectral map of a sample. The first time-domain broadband SOCT technique used the spectral-centroid shift as the indicator of spectral modification, to detected optical absorption by melanin in an African frog tadpole [9]. Later, depth-resolved backscattered spectra and tissue transfer functions were measured 1-3 Scope of the Thesis 14 with high precision using a Fourier-Domain OCT system, which enabled quantitative estimation of absorber concentration [10]. SOCT has the potential to become a powerful extension of OCT with applications such as the assessment of blood oxygen saturation [6]. One promising application is scatterer size and concentration measurement for the detection of early dysplastic changes using Mie theory [11], or angle-resolved low-coherence interferometry (aLCI), a related technique [12]. 1-3 Scope of the Thesis The goal of this thesis is to introduce a novel method for spectral analysis of OCT signals which can be used for scatterer size estimation and classification. Chapter 2 is a review of the fundamental operating principles and theory behind OCT. In Chapter 3, Mie scattering theory is reviewed to understand the basis for using spectral modulation as a diagnostic feature in SOCT. Chapter 4 discusses basic issues in SOCT, such as speckle, instrumentation and fabrication of tissue phantoms. Chapter 5 discusses spectral analysis techniques that have be used in this study. Chapter 6 discusses the experimental results, a comparison is given between the methods that have been used and the results are thoroughly discussed. Finally, the thesis is summarized and future studies are described in Chapter 7. Chapter 2 Optical Coherence Tomography 2-1 Introduction Optical Coherence Tomography (OCT) is a modern non-invasive biomedical imaging technique that generates in vivo cross-sectional images of tissue microstructure with micron-scale spatial resolution [1]. OCT has its roots in white-light interferometry that led to the development of Optical Coherence-Domain Reflectometry (OCDR), an 1-d optical ranging technique. OCDR uses a low coherence source to perform optical ranging by detecting interference reflected by the reference and sample arm. It was developed originally for finding faults in fiberoptic cables and network components [13, 14]. Resolutions up to 10 µm and a dynamic range of 120 dB were demonstrated with OCDR [15]. The first biological applications were in the field of the ophthalmology, where OCDR was used to obtain structural measurements from the eye [16, 17] and from other biological tissues [18, 19]. Later OCDR was extended to obtain 2-dimensional images and OCT was created [1]. OCT was rapidly developed to a clinically viable instrument and the first medical applications were reported [20, 21, 22]. OCT is analogous to ultrasound B-mode imaging except that it uses infrared light, back-scattered from microstructures of the tissue for generating images. OCT is using the principle of Low Coherence Interferometry (LCI) along with optical heterodyne detection to obtain high axial resolution and high sensitivity to weakly backscattered light from the sample. At the heart of the OCT is an interferometer illuminated by a broadband light source. The typical OCT system (Figure 2.1), uses a fiber based Michelson interferometer for splitting the light source beam into a reference and a sample arm. The reference beam is retroreflected from a scanning reference mirror at a known distance and returns to the detector, where it is recombined with the sample beam. The relative optical path difference between sample and reference arm is contained in the interference signal, which is detected at the photodetector. Subsequently, by signal processing electronics and computer data 2-2 Time-Domain OCT (TD-OCT) 16 acquisition, the position of reflective boundaries within the sample can be precisely detected and generate 2-dimensional images. This section will derive the Fourier transform relationship between the power spectrum of the light source and the axial Point Spread Function (PSF). A discussion will be given for the effect of chromatic dispersion on the axial resolution. The discussion follows derivations in the text edited by Bouma and Tearney [23]. reference mirror SLD 50/50 Beam Splitter PC D photoreceiver sample Figure 2.1: Schematic of Time Domain OCT system with a moving mirror in the reference arm. 2-2 Time-Domain OCT (TD-OCT) 2-2.1 Interferometer with Coherent Light Consider the simplified schematic of the Michelson interferometer [24, 25] shown in Figure 2.2. Light leaving from the source can been described as a plane wave propagating in the z -direction α1 = A exp(−jkz) where (2.1) 2π (2.2) λ Then α1 enters in the interferometer and is divided at a beamsplitter into reference k= 2-2 Time-Domain OCT (TD-OCT) 17 and sample arms. Beamsplitters, mirrors and in general all the mediums can be described by a scattering matrix (ABCD Matrix): −r jt jt −r ! (2.3) where r is the reflectivity and t is the transmission. For the 50/50 beamsplitter the ABCD matrix is: ! √j − √12 2 (2.4) √j √1 − 2 2 The two planes b1 and b2 exiting from the beamsplitter are: b1 b2 ! = √j 2 √ − 12 − √12 √j 2 ! a1 0 ! − √12 α1 = √j 2 ! (2.5) α1 The two fields are then reflected from the moving mirror (reference arm b2 ), and backscattered from the sample (sample arm b1 ). They recombine at the detector as ⎡ − rr ⎢ 0 ⎣ 0 ⎤ − rr ⎥⎦ Mirror lr b2 = − 1 a1 2 1 a1rr exp ( − jklr ) 2 ls b1 = a1 Source Beam Splitter Es = ⎡ ⎢− ⎢ ⎢ ⎣⎢ 1 2 j 2 j ⎤ 2 ⎥ ⎥ 1 ⎥ − 2 ⎦⎥ − j a1 2 j a1rs exp ( − jkls ) 2 ⎡ − rs ⎢ jt ⎣ s Sample 1 j 1 j a1rs exp ( − jkls ) Er = a1rr exp ( − jklr ) 2 2 2 2 Detector Figure 2.2: The Michelson interferometer. jts ⎤ − rs ⎥⎦ 2-2 Time-Domain OCT (TD-OCT) 18 one field Ed = Er + Es = Ed = j (α1 rr exp(−2jklr ) + α1 rs exp(−2jkls )) 2 j (Ar exp(−2jklr ) + As exp(−2jkls )) 2 (2.6) (2.7) The detector measures only irradiance and not the electric field so the absolute of the Equation 2.7 must be taken to obtain the photocurrent of the detector Id = |Ed Ed∗ | = Id = 1 [|Er Er∗ | + |Es Es∗ | + Es Er∗ + Er Es∗ ] 4 1 |As |2 + |Ar |2 + As A∗r exp (2jk(lr − ls )) + Ar A∗s exp (2jk(ls − lr )) 4 (2.8) (2.9) With the use of the trigonometry identity cos(θ) = 21 (exp(jθ) + exp(−jθ)) and by taking only the real part Equation 2.9 becomes Id = 1 |As |2 + |Ar |2 + <{As A∗r + Ar A∗s }cos(2k∆l) 4 (2.10) where ∆l = lr − ls (2.11) ∆l is the mismatch in distance between the reference and sample beam paths. Equation 2.10 shows that the photocurrent of the detector has two components, a DC and an AC component. The DC component (As , Ar ) is proportional to the reflectance from each arm and AC component is sinusoidally modulated as a function of the pathlength difference (∆l) between the two arms with an amplitute proportional to the reflectivity of the sample arm. This component represents the interference between the two arms because it contains all the backscattered information from the sample. Replacing the wavenumber k in Equation 2.10 reveals that the cosine term has a period of λ/2 relative to the length mismatch ∆l (Figure 2.3). Also, depending on the pathlength mismatch, constructive or destructive interference occurs at the detector π ∆l 1 ) Iinter = <{As A∗r + Ar A∗s }cos( 4 λ/2 (2.12) The interference signal depends on the match between sample and reference fields (Es , Er∗ ), and can be described by a cross correlation Iinter ∝ <{Es Er∗ } (2.13) With TD-OCT, the mirror in the reference arm is moving with velocity ∆l = 2-2 Time-Domain OCT (TD-OCT) 19 Figure 2.3: Interferometric pattern resulting from moving the reference arm and using a coherent source. Interferometric pattern resulting from moving the reference arm and using a low coherence source. 2vm t and therefore a Doppler shift fD occurs fD = 2vm λ (2.14) So Equation 2.12 becomes: Iinter 2-2.2 1 = <{As A∗r + Ar A∗s }cos(2πfD t) 4 (2.15) Interferometer with Low Coherence Light Section 2-2.1 describes interferometry with a monochromatic source. Equation 2.15 gives the photocurrent at the detector with a 50/50 beamsplitter and a moving mirror in the reference arm. Low Coherence Interferometry (LCI), using a broad bandwidth source of a finite bandwidth of frequencies rather than just a single frequency requires a modification of Equation 2.12. First a low coherence source can be represented as the sum of monochromatic sources: Z ∞ A(k)exp(−jkz)dk α1 = (2.16) −∞ The electric fields from the sample Es and reference Er can be represented as functions of frequency: Er = Ar (ω)exp(−2jkr (ω)lr ) (2.17) Es = As (ω)exp(−2jks (ω)ls ) (2.18) In this case the field at the detector will be: Z ∞ Z ∞ j Ed = Ar (ω)exp(−2jkr (ω)lr )dω + As (ω)exp(−2jks (ω)ls )dω (2.19) 2 −∞ −∞ 2-2 Time-Domain OCT (TD-OCT) 20 The interference signal, as shown before (Equation 2.13), is: Iinter Iinter ∝ <{Es Er∗ } Z ∞ ∗ Iinter ∝ < Es Er dω −∞ Z ∞ ∝< S(ω)exp (−j∆φ(ω)) dω (2.20) (2.21) (2.22) −∞ where S(ω) = As (ω)Ar (ω) (2.23) ∆φ(ω) = 2ks (ω)ls − 2kr (ω)lr (2.24) and 2-2.3 Nondispersive Medium To examine the behavior in non-despersive media the reference and sample arm are considered uniform, linear, and non-dispersive. The spectrum of the light source S(ω − ω0 ) is also considered to be bandlimited with a center frequency of ω0 . As a result the propagation constants in each arm can be considered equal and can be re-written using a first order Taylor expansion around ω0 0 kr (ω) = ks (ω) = k(ω0 ) + k (ω0 )(ω − ω0 ) (2.25) Inserting this to the Equation 2.22 gives: Iinter ∞ d(ω − ω0 ) S(ω − ω0 )exp(−j(ω − ω0 )∆τg ) ∝ < exp(−jω0 ∆τp ) 2π −∞ Z (2.26) where the phase delay mismatch ∆τp and the group delay mismatch ∆τg are defined as 2∆l k(ω0 ) ∆τp = 2∆l = (2.27) ω0 vp 0 ∆τg = 2∆l k (ω0 ) = 2∆l vg (2.28) Assuming that the sample and reference arm fields have the same spectral components as the light source, S(ω) is related to the power spectrum of the source: Z ∞ S(ω) = G(τ )exp(−jωτ )dτ (2.29) −∞ where G(τ ) is the complex temporal coherence function of the source. Using this relation to Equation 2.26 with the Wiener − Khinchin theorem [26] it can be 2-2 Time-Domain OCT (TD-OCT) 21 obtained that Iinter ∝ < {exp(−jω0 ∆τp )G(τ )} (2.30) Iinter ∝ |G(τ )|cos(ω0 ∆τp ) (2.31) It follows that the interference signal depends on the temporal-coherence characteristics of the source. Also the interference signal consists of a carrier and an envelope. The carrier oscillates with increasing path length mismatch 2∆l at a spatial frequency k(ω0 ) and the envelope is described by Equation 2.31 and determines the axial point spread function of the interferometer. 2-2.4 OCT Resolution It follows from the Equation 2.22 that the shape and width of the emission spectrum of the light source are important variables in OCT. Laser sources with a broad band spectrum can produce interference patterns of short temporal and spatial extent. The relationship between S(ω) and G(τ ) from Equation 2.29, when both are represented by gaussian functions, can be used to verify this as follows: s S(ω − ω0 ) = 2π ω − ω0 exp − σω2 2σω2 (2.32) The Fourier transform will give the interferometric signal according to Equation 2.31 2 2 π ∆τ Iinter ∝ exp − cos(ω0 ∆τp ) (2.33) 2στ2 where the width is στ = 1 σω (2.34) For obtaining the coherence length of the light source or the axial resolution the Full Width Half Maximum (FWHM) of the gaussian function can be used. The width of the gaussian source (σω ) is related to the FWHM of the wavelength spectrum (∆λ) by: ∆ω 2πc∆λ σω = √ = 2√ (2.35) 2ln2 λ0 2ln2 Therefore the FWHM of the interference signal, i.e. the axial resolution, in free space will be lc = 2cln2 1 2ln2 λ20 = π σω π ∆λ 2 λ lc ≈ 0.44 0 ∆λ (2.36) (2.37) 2-2 Time-Domain OCT (TD-OCT) 22 The axial resolution depends on the coherence length, which depends on the light source spectrum. The SLD sources usually have Gaussian or near-Gaussian spectral shape. However, for ultrabroadband laser sources such as the Ti:sapphire and nonlinear fiber sources, the spectral shapes are often not Gaussian and the coherence length is numerically calculated: Z ∞ c S 2 (ω)dω lc = Z 0∞ 2 S(ω)dω (2.38) 0 The transverse resolution of OCT depends on the optics used and is usually defined as the diameter of a gaussian beam, i.e. 2w: r 2w = 2bλo π (2.39) where b is the confocal parameter of the system. It can be shown that if the focal length of the sample lens is f and the beam diameter incident onto the sample lens is D , then 4f λ2o (2.40) w2 = πD2 Therefore the focal length f of the lens in the sample arm should be chosen carefully to meet both resolution and focusing depth requirements. 2-2.5 Group Velocity Dispersion The light propagating from the source will experience Group Velocity Dispersion (GVD) from the fibers, lens, and the specimen. The dispersion will affect the envelope of the interferometric pattern and the axial resolution of the OCT system. To examine the effect of GVD, the propagation constant must be expanded to a second order Taylor series around ω0 : 0 00 kr (ω) = ks (ω) = k(ω0 ) + k (ω0 )(ω − ω0 ) + k (ω0 )(ω − ω0 )2 (2.41) Assuming that a GVD mismatch exists in a length L of the sample and reference arms then the effect of GVD to phase mismatch from Equation 2.24 is: 1 00 0 ∆φ(ω) = k(ω0 )2∆l + k (ω0 )(ω − ω0 )2∆l + ∆k (ω0 )(ω − ω0 )2 (2L) 2 (2.42) where 00 00 00 ∆k (ω0 ) = kr (ω) − ks (ω) is the GVD mismatch. (2.43) 2-3 Optical Sources 23 Inserting ∆φ(ω) into the Equation 2.22 and neglecting the real operator the interference pattern becomes: Z ∞ S(ω − ω0 ) Iinter ∝ exp(−jω0 ∆τp ) −∞ 1 00 d(ω − ω0 ) 2 exp −j ∆k (ω0 )(ω − ω0 ) (2L) exp(−j(ω − ω0 )∆τg ) (2.44) 2 2π The effect of the dispersive medium is to broaden the interferometric signal and induce assymetry due to chirp in the two interferometer arms. Assuming, again, a gaussian spectrum for comparison with Section 2-2.3 the resulting interferometric signal will be Iinter ∆τg2 στ exp − exp(−jω0 ∆τp ) = Γ(2L) Γ(2L)2 (2.45) where Γ(2L)2 is a complex function 00 Γ(2L)2 = στ2 + j∆k (ω0 )(2L) (2.46) The Gaussian function in Equation 2.45 has a real and an imaginary part defining an envelope change as well as a chirp. Inserting Equation 2.46 and taking the real part reveals that the gaussian envelope is broadened to the new width 2σ˜τ " 2σ˜τ = 2στ 1 + where τcritical στ 4 #1/2 00 1/2 τcritical = ∆k (ω0 )(2L) (2.47) (2.48) Significant broadening will be present when τcritical > 1 which implies that in the case of air vs. some other material even a few mm are enough to significantly broaden the PSF. Dispersion mismatch also decreases the amplitude of the interferometric envelope, as described by the multiplicative factor 1 στ = 1/4 Γ(2L) 1 + (τcritical /στ )4 2-3 (2.49) Optical Sources The results of several theoretical and experimental studies cited in Section 2-2 show the importance of the light source on the performance of the OCT system. The general requirements are 2-3 Optical Sources 24 1. wavelength, 2. bandwidth, 3. single-transverse-mode power. The first requirement rises from the need to operate in a spectral range in which the penetration of light into tissue is adequate. The near-infrared end of the spectrum is known as the therapeutic or diagnostic window, even if water absorption increases there (Figure 2.4). Theoretical [22, 27] and experimental studies [21, 28, 29] in OCT are suggesting that the optimal image depth of penetration should occur with sources emitting from 1200 nm to 1650 nm due to the fact that scattering losses decrease in that range while water absorption is still relative low Figure 2.4: Spectral absorption of some tissue molecules, and of aortic tissue. The brightened wavelength ranges have already been used in OCT [30]. Axial resolution in OCT imaging is determined by the bandwidth of the light source as described in Equation 2.37, lc ≈ 0.44 λ20 ∆λ (2.50) where λ0 is is the source center wavelength and ∆λ is the full width at half-maximum (FWHM) spectral width. In general the broader the emission bandwidth of the source the better the resolution that can be achieved. The mismatches between the optical dispersion of the reference and sample arms [31] and the chromatic aberration of the focused beam caused by scattering in the tissue [32]. Have to be considered and compensate for by the selection of the source. Also the shape of the 2-3 Optical Sources 25 Table 2.1: Short coherent sources suitable for use in OCT systems [34] Source edge-emitting LED Center Bandwidth Wavelength (nm) (nm) 1300, 1550 50-100 Emission Power Reference 20-300µW Derickson et al. [35] superluminescent diodes (SLD) 800 1300 20-30 40-50 1-10mW 1-5mW ...... ...... Multiple QW LED/SLD 800 ‘1400 90 90 15mW max 5mW max Lin and Lee [36] Poole et al. [37] Laser pumbed fluorescent organic dye 590 40 9mW Liu et al. [38] Mode-Locked T i : Al2 O3 laser 820 50-145 400mW Bouma et al. [39] Mode-Locked Cr : forsterite laser 1280 75 30mW Tearney et al. [40] 1550 1800 1060 40-80 80 65 10-100mW 7mW 108mW Bouma et al. [28] ...... Paschotta et al. [41] 4+ Superfluorescent optical fibers: Er-doped Tm-doped Nd/Yb-doped spectrum of the source is an important variable since real sources are not perfectly Gaussian and may result significant sidelobes which, in turn, limit the dynamic range of the scanner near strong reflections [33]. The power required from an optical source is constrained by the relation [23, chap. 2] : SN R vs = const. (2.51) Ps ∆L where SN R is the signal-to-noise ratio (or sensitivity), vs is proportional to the axial scanning acquisition rate, and Ps is the maximum source optical power that can reach the detector. This relation implies that for obtaining higher acquisition rate and higher sensitivity requires an increased source power. Usually singlemode optical sources are used and the source power concentrated is limited by the requirement that the diameter D of the source and its half-angle of emission α be 2-3 Optical Sources 26 related to the center wavelength [42] as follow Dα = λ0 (2.52) Therefore, the most effective sources for OCT imaging emit light from a small spot over a wide angle or from a large spot over a narrow angle. In Table 2.1 sources suitable for use in OCT systems are listed [34]. The most commonly used sources are edge-emitting light-emitting diodes (ELED) and superluminescent diodes (SLD), with center wavelengths in either the 800or1300 nm. SLD are the most commonly used because of their high power and relatively low cost, but the coherence lengths of SLD (typically 15 − 30 µm) are not short enough to achieve the resolution required for many medical applications. Efforts have been made to overcome this disadvantage, one example is synthesizing a broadband source by combining the outputs of several SLD with different center wavelengths [43]. Also multiple quantum-well devices achieve this synthesis by coupling the output of several sources on a single substrate [36, 37]. Chapter 3 Mie Theory 3-1 Introduction In 1908, Gustav Mie [44] developed a theory in an effort to understand the varied colors in absorption and scattering exhibited by small colloidal particles of gold suspended in water. Mie theory provides insight into the biological origin of OCT signals, and justifies the choice of spectral modulation as an analysis technique. Measuring spectral modulation to determine the scatterer size and distribution had been used extensively to the area of Light Scattering Spectroscopy (LSS). Significant research in LSS has been carried out for measuring the size of scatterers in tissue structures [45, 46] and to detect malignancies in-vivo [47] and in-situ [48, 49] and to characterize particle size using tissue phantoms [50, 51]. The central idea behind this research is that cellular organelles of epithelial tissue can be considered as spherical particles whose interactions with light are described by Mie theory [52, 53]. The discussion begins with a general description of the scattering problem, and a solution of Maxwell’s equations on spherical coordinates. Next a set of harmonics vector solutions for the vector wave equation is presented. These functions provide a complete orthogonal basis for expressing a plane wave as an infinite series. Subsequently the expansion coefficients for the infinite series and solutions for the scattered field of a spherical particle are derived. The most interesting part for OCT is the relation between backscattered intensity and illuminating wavelength. The discussion of Mie theory follows derivations in the texts by Bohren and Huffman [54] and de Hulst [55]. 3-2 General Formulation of the Problem The problem is defined as having a particle of specified size, shape and optical properties that is illuminated by an arbitrarily polarized monochromatic wave. The electromagnetic field at all points in the particle and at all points of the homogeneous 3-2 General Formulation of the Problem 28 medium in which the particle is embedded must be determined. The field inside the particle is defined as (E1 ,H1 ) and the medium surrounding field as (E2 ,H2 ), which is the superposition of the incident field (Ei ,Hi ) and the scattered field (Es ,Hs ) (Figure 3.1). E2 = Ei + Es H2 = Hi + Hs (3.1) Hi = H0 exp(ik · x − iωt) (3.2) where Ei = E0 exp(ik · x − iωt) and k is the wave number of the surrounding medium. Figure 3.1: The incident field (Ei ,Hi ) gives rise to a field (E1 ,H1 ) inside the particle and a scattered field (Es ,Hs ) in the medium surrounding the particle. The fields must satisfy the Maxwell equations ∇·E=0 (3.3) ∇·H=0 (3.4) ∇ × E = jωµH (3.5) ∇ × H = −jωE (3.6) at all points where and µ are continuous. The curl of Equation 3.5 and 3.6 is ∇ × (∇ × E) = jωµ∇ × H = ω 2 µE∇ × (∇ × H) = −jω∇ × E = ω 2 µH (3.7) 3-2 General Formulation of the Problem 29 and using the vector identity ∇ × (∇ × A = ∇(∇ · A) − ∇ · (∇A)) (3.8) results in ∇2 E + k 2 E = 0 ∇2 H + k 2 H = 0 (3.9) where k 2 = ω 2 µ and ∇2 A = ∇(∇ · A). Thus, E and H satisfy the vector wave equation in a linear, isotropic, homogeneous medium, are also be divergence-free ∇·E=0 ∇·H=0 (3.10) In addition E and H are not independent as evident, from Equations 3.5 and 3.6. 3-2.1 Boundary Conditions The electromagnetic field must satisfy Maxwell’s equations at points where and µ are continuous. But on the boundary between particle and medium there is a sudden change in these properties, i.e. a discontinuity. At such boundary points the following conditions on the fields are imposed: b=0 [E2 (x) − E1 (x)] × n (3.11) b=0 [H2 (x) − H1 (x)] × n (3.12) b is the outward directed normal to the surface S of the particle. The boundwhere n ary conditions require that the tangential components of E and H are continuous across a boundary separating media with different properties. b , which is the boundary Consider a closed surface A, with outward normal n between regions 1 and 2 (Figure 3.2). The rate at which electromagnetic energy is transferred across a closed surface arbitrarily near A in region 1 is Z A Z b dA = S1 · n A b · (E1 × H1 ) dA n (3.13) Similarly, the rate of electromagnetic energy transfer across a closed surface arbitrarily near A in region 2 is Z A Z b dA = S2 · n A b · (E2 × H2 ) dA n (3.14) 3-2 General Formulation of the Problem 30 Figure 3.2: Closed surface separating regions 1 and 2. b = E1 × n b , H2 × n b = H1 × n b If the boundary conditions are imposed, then E2 × n and the integrals 3.13 and 3.14 may be written ZA A Z Z Z b dA = S1 · n b dA = S2 · n H1 · (b n × E1 )dA = H1 · (b n × E2 )dA (3.15) H1 · (b n × E2 )dA (3.16) ZA ZA E2 · (b n × H2 )dA = A A where we have used the permutation rule for the triple scalar product A · (B × C) = B · (C × A) = C · (A × B) 3-2.2 (3.17) Solutions to the vector wave equations Suppose that, given a scalar function ψ and an arbitrary constant vector c, a vector function M is constructed M = ∇ × (cψ) (3.18) and ∇·M=0 (3.19) If the vector identities are used ∇ × (A × B) = A(∇ · B) − B(∇ · A) + (B · ∇)A − (A · ∇)B (3.20) 3-2 General Formulation of the Problem ∇(A · B) = A × (∇ × B) + B × (∇ × A) + (B · ∇)A + (A · ∇)B 31 (3.21) result in ∇2 M + k 2 M = ∇ × [c(∇2 ψ + k 2 ψ)] (3.22) If ψ is a solution to the scalar wave equation, then M satisfies the vector wave equation. From M we can construct N N= ∇×M k (3.23) with zero divergence, which also satisfies the vector wave equation ∇2 N + k 2 N = 0 (3.24) ∇ × N = kM (3.25) results in So M and N have all the required properties of an electromagnetic field: 1. they satisfy the vector wave equation, 2. they are divergence-free, 3. the curl of M is proportional to N, 4. the curl of N is proportional to M. Thus, the problem of finding solutions to the field equations reduces to the comparatively simpler problem of finding solutions to the scalar wave equation. We shall call the scalar function ψ a generating function for the vector harmonics M and N, the vector c is sometimes called the guiding or pilot vector. Scattering by a sphere required functions ψ that satisfy the wave equation in spherical polar coordinates, r, θ and φ (Figure 3.3). For pilot function radius vector r is defined which M = ∇ × (rψ) (3.26) Thus M becomes a solution to the vector wave equation in spherical polar coordinates and so is the associated N. The scalar wave equation in spherical polar coordinates is 1 ∂ 1 ∂ ∂ψ 1 ∂ 2ψ 2 ∂ψ r + sinθ + + k2ψ = 0 (3.27) r2 ∂r ∂r r2 sinθ ∂θ ∂θ r2 sinθ ∂φ2 A separation of variables is first performed ψ(r, θ, φ) = R(r)Θ(θ)Φ(φ) (3.28) 3-2 General Formulation of the Problem 32 Figure 3.3: Scattering by a spherical particle When substituted into 3.27 and by dividing by ψ(r, θ, φ) gives 1 d Rr2 dr 1 d dΘ 1 d2 Φ 2 dR r + sinθ + + k2 = 0 dr Θr2 sinθ dθ dθ Φr2 sin2 θ dφ2 (3.29) By multiplying by r2 sin2 θ the azimuthal part can be isolated 1 d 1 d dΘ 1 d2 Φ 2 2 2 2 dR = r sin θ −k − r − sinθ Φ dφ2 Rr2 dr dr Θr2 sinθ dθ dθ (3.30) The variable φ can separated with a separation constant m 1 d2 Φ = −m2 Φ dφ2 thus 1 d R dr r 2 dR dr 1 d +r k =− Θsinθ dθ 2 2 (3.31) dΘ m2 sinθ + dθ sin2 θ (3.32) The variables are separated. Each side is equated to a constant n(n+1), and finally obtain 1 d dΘ m2 sinθ − Θ + n(n + 1)Θ = 0 (3.33) sinθ dθ dθ sin2 θ 1 d 2 dR (r ) + k 2 r2 R − n(n + 1)R = 0 (3.34) R dr dr 3-2 General Formulation of the Problem 33 A partial differential equation of three variables has been replaced by three ordinary differential equations. The azimuthal solution Φ(φ) is consided first, beginning with the requirement that is single-valued Φ(φ + 2π) = Φ(φ) (3.35) Because of the periodicity of the azimuthal solution, m is a constant. The linearly independent solutions are Φe = cosmφ, Φo = sinmφ, (3.36) where subscripts e and o denote even and odd. For the other two equations, the solution is going to be a little more complex. Equation 3.33 is actually the associated Legendre equation and Equation 3.34 after a substitution becomes the spherical Bessel equation. We shall begin with the associated Legendre: dP m (cosθ) m2 1 d (sinθ n ) + [n(n + 1) − ]P m (cosθ) = 0 sinθ dθ dθ sin2 θ n (3.37) One way of developing the solution of the associated Legendre equation is to start with the regular Legendre equation and convert it to the associated by using multiple differentiation. Inserting x = cosθ to the Equation 3.33 transforms to (1 − x2 ) d m m2 d m P (x) − 2x P (x) + [n(n + 1) − ]P m (x) = 0 dx2 n dx n 1 − x2 n (3.38) The Legendre equation is 00 0 (1 − x2 )Pn − 2xPn + n(n + 1)Pn = 0 (3.39) with solutions the Legendre polynomials Pn (cosθ) and after differentiate m times the result is 00 0 (1 − x2 )u − 2x(m + 1)u + (n − m)(n + m + 1)u = 0 (3.40) where dm Pn (x) (3.41) dxm Equation 3.40 is not self-adjoint [56]. To put it into self-adjoint form and convert the weighting function to unity, u(x) must be replaced by u≡ v(x) = (1 − x2 )m/2 u(x) = (1 − x2 )m/2 dm Pn (x) dxm (3.42) 3-2 General Formulation of the Problem 34 Solving for u and differentiating: mxv )(1 − x2 )−m/2 , 2 1−x 0 2mxv mv m(m + 2)x2 v 00 u = [v + + + ](1 − x2 )−m/2 2 2 2 2 1−x 1−x (1 − x ) 0 u = (v + (3.43) (3.44) Substituting into Equation 3.40 we find that the new function v satisfies the selfadjoint ordinary differential equation 00 0 (1 − x2 )v − 2xV + [n(n + 1) − m2 ]v = 0 1 − x2 (3.45) which is the associated Legendre with solutions the m times differentiate Legendre polynomials, the so called associated Legendre polynomials. Pnm (cosθ) = (1 − cos2 θ)m/2 dm Pn (cosθ) dxm (3.46) For Equation 3.34, to transform it into a Bessel equation, substitute R(kr) = which results r2 Z(kr) (kr)1/2 d2 Z dZ 1 +r + [k 2 r2 − (n + )2 ]Z = 0 2 dr dr 2 (3.47) (3.48) which is a Bessel equation, Z is a Bessel function of order n + 12 . The linearly independent solutions to Equation 3.48 are the Bessel functions of first, second and third kind Jn , Nn Hn . It is convenient to label these functions spherical Bessel functions r π jn (x) = Jn+1/2 (x) (3.49) 2x r r π π n+1 nn (x) = Nn+1/2 (x) = (−1) J−n−1/2 (x) (3.50) 2x 2x r π (1) (1) hn (x) = H (x) = jn (x) + inn (x) (3.51) 2x n+1/2 r π (2) (2) hn (x) = H (x) = jn (x) − inn (x) (3.52) 2x n+1/2 The spherical Bessel functions satisfy the recurrence relations d n+1 [x fn (x)] =xn+1 fn−1 (x) dx d −n [x fn (x)] = − x−n fn+1 (x) dx (3.53) (3.54) 3-2 General Formulation of the Problem (1) 35 (2) Here fn may represent jn , nn hn or hn . From the first two orders sin r sin r cos r , j1 (r) = 2 − r r r cos r sin r cos r , n1 (r) = − 2 − n0 (r) = − r r r j j j (1) (1) h0 (r) = − exp(jr), h1 (r) = exp(jr) − − 2 r r r j0 (r) = (3.55) (3.56) (3.57) higher-order functions can be generated by recurrence. Now generating functions can be constructed that satisfy the scalar wave equation in spherical polar coordinates: ψemn = cos mφ Pnm (cos θ)zn (kr) (3.58) ψomn = sin mφ Pnm (cos θ)zn (kr) (3.59) (1) (2) where zn is any of the four spherical Bessel functions jn , nn hn or hn . The vector spherical harmonics generated by ψemn and ψomn Memn = ∇ × (r ψemn ), ∇ × Memn , k which in component form are Nemn = Momn = ∇ × (r ψomn ), Nomn = ∇ × Momn , k (3.60) (3.61) Memn = −m dP m (cos θ) sin mφ Pnm (cos θ)zn (kr)b eθ − cos mφ n zn (kr)b eφ , sin θ dθ (3.62) Momn = −m dP m (cos θ) cos mφ Pnm (cos θ)zn (kr)b eθ − sin mφ n zn (kr)b eφ , sin θ dθ (3.63) Nemn = Nomn = −zn (kr) cos mφ n(n + 1)Pnm (cos θ)b er kr dPnm (cos θ) 1 d + cos mφ [krzn (kr)]b eθ dθ kr d(kr) Pnm (cos θ) 1 d − m sin mφ [krzn (kr)]b eφ , (3.64) sin θ kr d(kr) zn (kr) sin mφ n(n + 1)Pnm (cos θ)b er kr dP m (cos θ) 1 d + sin mφ n [krzn (kr)]b eθ dθ kr d(kr) 3-3 Expansion of a plane wave in vector spherical harmonics + m cos mφ 36 Pnm (cos θ) 1 d [krzn (kr)]b eφ , (3.65) sin θ kr d(kr) With these vector harmonics can be solved the problem of scattering by an arbitrary sphere. 3-3 Expansion of a plane wave in vector spherical harmonics First, consider a plane x- polarized wave, written in spherical polar coordinates as Ei = E0 exp(jkr cos θ)b ex (3.66) b ex = sin θcosφb er + cos θ sin φb eθ − sin φb eφ (3.67) where by an arbitrary sphere. The first step toward the solution to this problem is expanding equation 3.66 in vector spherical harmonics: Ei = ∞ X ∞ X (Bemn Memn + Bomn Momn + Aemn Nemn + Aomn Nomn ) (3.68) m=0 n=m Because sin mφ is orthogonal to cos m0 φ for all m and m0 it follows that Memn and Momn are orthogonal. Z 2π Z π Mem0 n0 Momn sin θdθdφ = 0 0 (all m, m’, n, n’) (3.69) 0 Similarly, (Nomn , Nemn ), (Momn , Nomn ) and (Memn , Nemn ) are mutually orthogonal sets of functions. The orthogonality of all the vector spherical harmonics implies that the coefficients in the expansion are of the form 2π Z π Z Ei · Memn sin θdθdφ 0 0 Bemn = Z 2π (3.70) π Z 2 |Memn | sin θdθdφ 0 0 2π Z π Z Ei · Momn sin θdθdφ 0 Bomn = Z 0 2π Z (3.71) π 2 |Momn | sin θdθdφ 0 0 3-4 The internal and scattered fields 2π Z 37 π Z Ei · Nemn sin θdθdφ 0 0 Aemn = Z 2π (3.72) π Z 2 |Nemn | sin θdθdφ 0 0 2π Z π Z Ei · Nomn sin θdθdφ 0 0 Aomn = Z 2π Z (3.73) π 2 |Nomn | sin θdθdφ 0 0 It follows from Equations 3.62-3.65 together with the the orthogonality of the sine and cosine that Bemn = Aomn = 0,for all m, n (3.74) Bomn = Aemn = 0,for all m = 1 (3.75) The incident field is finite at the origin, which requires that the spherical Bessel jn and nn will be also finite at origin. That is the reason why nn is rejected, because of its misbehavior at the origin. Following the notation of [54, 55] a superscript (1) is appended to the vector spherical harmonics for specifying the radial dependence by jn . Thus, the expansion for Ei , has the form Ei = ∞ X (1) (1) (Boln Moln + Aeln Neln ) (3.76) n=1 By intergrating Equations 3.70 and 3.72 the coefficients Boln and Aeln are obtained 2n + 1 n(n + 1) 2n + 1 = −jE0 j n n(n + 1) Boln = j n E0 (3.77) Aeln (3.78) This leads to the expansion of plane wave in spherical harmonics Ei = E 0 ∞ X n=1 3-4 jn 2n + 1 (1) (1) (Moln − jNeln ) n(n + 1) (3.79) The internal and scattered fields Suppose that a plane x-polarized wave is incident on a homogeneous, isotropic sphere of radius a (Figure 3.3). As shown, the incident electric field may be expanded in an infinite series of vector spherical harmonics. The corresponding inci- 3-4 The internal and scattered fields 38 dent magnetic field is obtained from the curl of Equation 3.79 ∞ −k X n 2n + 1 (1) (1) E0 j (Meln + jNoln ) Hi = ωµ n=1 n(n + 1) (3.80) The scattered electromagnetic field (Es , Hs ) and the field (E1 , H1 ) inside the sphere in vector spherical harmonics may also be expanded. At the boundary between the sphere and the surrounding medium the following conditions are imposed (Ei + Es − E1 ) × b er = (Hi + Hs − H1 ) × b er = 0 (3.81) The expansion of the field (E1 , H1 ) can be calculated by using the orthogonality of the vector harmonics, the boundary conditions 3.81 and the form of expansion of the incident field. The field must be finite at the origin so we take jn (k1 r), where k1 is the wavenumber inside the sphere. E1 = ∞ X (1) (1) En (cn Moln − jdn Neln ) n=1 ∞ −k1 X (1) (1) En (dn Meln − jcn Noln ) H1 = ωµ1 n=1 (3.82) where µ1 is the permeability of the sphere and En = j n E0 (2n + 1) n(n + 1) (3.83) The scattered field does not exist at the origin, so both functions jn and nn are involved in the expansion of the scattered field. It is convenient now to switch to (1) (2) spherical Hankel functions (spherical Bessel of third kind), hn and hn for values of kr2 n2 (−j)n exp(jkr) h(1) (kr) ∼ n jkr (3.84) n (j) exp(jkr) (2) hn (kr) ∼ − jkr These asymptotic expressions describe a spherical wave travelling away from the (1) (2) origin hn and a spherical wave travelling towards the origin hn . For the scatterred (1) field one can use only hn as a generating function, therefore the expansion of the field is ∞ X (3) (3) Es = En (jan Neln − bn Moln ) n=1 ∞ X k Hs = ωµ n=1 (3.85) (3) En (jbn Noln + (3) an Meln ) 3-4 The internal and scattered fields 39 (1) The superscript (3) specifies the radial dependence by the spherical Hankel hn . 3-4.1 Angle-Dependent Functions It is now convenient to define the angle dependent functions for deriving more compactly the expressions πn = Pn1 , sinθ τ= dPn1 dθ (3.86) Upward recurrence relations for these functions can be developed n 2n − 1 cos θπn−1 − πn−2 n−1 n−1 τn = n cos θπn − (n + 1)πn−1 (3.87) πn = (3.88) Also the linear combinations of πn and τn are orthogonal sets of functions π Z Z 0 π (πn − τn )(πn − τn ) sin θdθ = 0 (m 6= n) (3.89) (πn + τn )(πn + τn ) sin θdθ = 0 The vector spherical harmonics(with m = 1), then are Moln = cos φ πn (cos θ)zn (kr)b eθ − sin φ τn (cosθ)zn (kr)b eφ (3.90) Meln = − sin φ πn (cos θ)zn (kr)b eθ − cos φ τn (cosθ)zn (kr)b eφ (3.91) zn (kr) b er kr 0 [krzn (kr)] b eθ + sin φ τn (cos θ) kr Noln = sinφ n(n + 1) sin θπn (cos θ) 0 [krzn (kr)] b + cos φπn (cos θ) eφ (3.92) kr zn (kr) b er kr 0 [krzn (kr)] b + cos φ τn (cos θ) eθ kr Neln = cos φ n(n + 1) sin θπn (cos θ) 0 [krzn (kr)] b − sin φπn (cos θ) eφ (3.93) kr It was shown how the functions jn and nn behave at the origin (θ = 0). It only remains for us to show the behavior of the functions πn and τn which determine the θ dependence of the fields. Polar plots of πn and τn for n = 1 − 5 are shown in Figure 3-4.1 (θ = 0, 2π). There exists a symmetry for all plots around x-axis, 3-4 The internal and scattered fields 40 which is expected because the scattering particle is spherical and the incident light is propagating along the axis of symmetry. Also as the n increases the number of lobes increases, and the width of the forward and back - scattered lobes is decreasing. Furthermore, the absence of a backscattering lobe in the polar plots of πn and τn indicates that they are negative for backward directions, and all plot have a forward lobe but the backscattered is vanished for alternative values of n. From the behavior of these functions it follows that the scattered field will be distributed in a smaller spatial area as the particle size increases and as the particle size increases there will be decreased backscattering and increased forward scattering. 3-4.2 Scattering Coefficients The next step is to obtain explicit expressions for the scattering coefficients. For a given n there are four unknown coefficients an , bn , cn , and dn . The four independent equations needed, which are obtained from the Equation 3.81 at the boundary r = α in component form: Eiθ + Esθ = E1θ Eiφ + Esφ = E1φ Hiθ + Hsθ = H1θ Hiφ + Hsφ = H1φ (3.94) To obtain the four linear equations in the expansion coefficients the orthogononality of sin φ and cos φ, the relations for the angle functions 3.89 the above boundary relations with the expansions for the internal and scattering fields 3.79, 3.80, 3.82 and 3.85 are required. Along with the vector harmonics Equations 3.90, 3.91, 3.92 and 3.93 eventually result in four independent linear equations jn (mx)cn + h1n (x)bn = jn (x), 0 0 (3.95) 0 µ[mxjn (mx)] cn + µ1 [xh1n (x)] bn = µ1 [xjn (x)] , (3.96) µmjn (mx)dn + µ1 h1n (x)αn = µ1 jn (x), (3.97) 0 0 [mxjn (mx)] dn + m[xh1n (x)] αn = m[xjn (x)], (3.98) where the prime indicates differentiation with respect to the argument in parentheses and the size parameter x and the relative refractive index m are x = kα = 2πN α , λ m= k1 N1 = k N (3.99) N1 and N are the refractive indices of particle and medium, respectively. The four simultaneous linear equations are easily solved for the coefficients of the field inside 3-4 The internal and scattered fields 41 10 10 5 5 0 0 5 5 10 10 15 10 5 0 5 10 15 10 10 5 5 0 0 5 5 10 15 10 5 0 5 10 15 15 10 5 0 5 10 15 15 10 5 0 5 10 15 15 10 5 0 5 10 15 15 10 5 0 5 10 15 10 15 10 5 0 5 10 15 10 10 5 5 0 0 5 5 10 10 15 10 5 0 5 10 15 10 10 5 5 0 0 5 5 10 10 15 10 5 0 5 10 15 15 10 8 10 6 4 5 2 0 0 2 5 4 6 10 8 15 10 15 10 5 0 a 5 10 15 b Figure 3.4: Polar plots of the first five angle-dependent functions πn (a) and τn (b) (n = 1, . . . , 5). All functions are plotted to the same scale. 3-5 Scattering Matrix 42 the particle 0 0 µ1 jn (x)[xh1n (x)] − µ1 h1n (x)[xjn (x)] cn = µ1 jn (mx)[xh1n (x)]0 − µh1n (x)[mxjn (mx)]0 0 (3.100) 0 µ1 mjn (x)[xh1n (x)] − µ1 mh1n (x)[xjn (x)] dn = µ1 m2 jn (mx)[xh1n (x)]0 − µh1n (x)[mxjn (mx)]0 (3.101) and the scattering coefficients 0 0 µm2 jn (mx)[xjn (mx)] − µ1 jn (x)[mxjn (mx)] an = µm2 jn (mx)[xh1n (x)]0 − µ1 h1n (x)[mxjn (mx)]0 0 (3.102) 0 µ1 jn (mx)[xjn (x)] − µjn (x)[mxjn (mx)] bn = µ1 jn (mx)[xh1n (x)]0 − µh1n (x)[mxjn (mx)]0 (3.103) The scattering coefficients can be simplified somewhat by introducing the RiccatiBessel functions: ψn (kr) = krjn (kr), ξn (kr) = krh1n (kr)) (3.104) If the permeability of the particle and the surrounding medium are considered to be the same, then 0 0 mψn (mx)ψn (x) − ψn (mx)ψn (mx) an = mψn (mx)ξn0 (x) − ξn (mx)ψn0 (mx) 0 (3.105) 0 ψn (mx)ψn (x) − mψn (mx)ψn (mx) bn = ψn (mx)ξn0 (x) − mξn (mx)ψn0 (mx) (3.106) Note that an and bn vanish as m approaches unity; this is as it should be: when the particle disappears, so does the scattered field. 3-5 Scattering Matrix The infinity series expansion, Equation 3.79 and 3.80 of the scattered field is assumed to be uniformly convergent, if nc terms are taken then the resulting error will be arbitrarily small for all kr if nc is sufficiently large. Also if kr n2c the 3-5 Scattering Matrix 43 asymptotic expressions of the spherical Hankel can be substituted h1n (kr) (−j)n ejkr , ∼ jkr kr n2 (3.107) dh1n (kr) (−j)n ejkr ∼ d(kr) jkr (3.108) in the truncated series; the resulting transverse components of the scattered electric field are ejkr cos φS2 (cos θ) −jkr ejkr sin φS1 (cos θ) ∼ −E0 −jkr Esθ ∼ E0 Esφ (3.109) (3.110) where X 2n + 1 (αn πn + bn τn ) n(n + 1) n X 2n + 1 S2 = (αn τn + bn πn ) n(n + 1) n S1 = (3.111) (3.112) and the series are terminated after nc terms. The resulting scattering matrix for the relation between incident and scattered field amplitudes is Eks E⊥s ! ejk(r−z) = −jkr S2 0 0 S1 ! Eki E⊥i ! (3.113) The relation between incident and scattered Stokes parameters   Is   Qs   = 1  U  k2 r2  s Vs    S11 S12 0 0 Ii    S12 S11   0 0    Qi   0   0 S33 S34     Ui  0 0 −S34 S33 Vi 1 S11 = (|S2 |2 + |S1 |2 ), 2 1 ∗ S33 = (S2 S1 + S2 S1∗ ), 2 1 S12 = (|S2 |2 − |S1 |2 ) 2 i S34 = (S1 S2∗ − S2 S1∗ ) 2 (3.114) (3.115) (3.116) 2 2 2 2 Only three of these four matrix elements are independent:S11 = S12 + S33 + S34 . From the Stokes parameters, the relation between incident light and the scattered light for unpolarized light is Is = S11 (θ)Ii , Qs = S12 (θ)Ii , Us = Vs = 0 (3.117) 3-6 Computation of Scattering Coefficients 44 where the factor 1/k 2 r2 was ommited. 3-6 Computation of Scattering Coefficients To obtain quantitative results from the Mie theory one must calculate the angular functions πn and τn together with the scattering coefficients an and bn and sum the series 3.111, 3.112 for the scattering matrix elements. However the scattering coefficients an and bn are complicated functions of spherical Bessel functions and their derivatives which make their computation cumbersome. To simplify Equations 3.105 and 3.106 the logarithmic derivative can be employed [57] d ln ψn (ρ) (3.118) Dn (ρ) = dρ which simplifies Equations 3.105 and 3.106 to an = [Dn (mx)/m + n/x] ψn (x) − ψn−1 (x) [Dn (mx)/m + n/x] ξn (x) − ξn−1 (x) (3.119) bn = [mDn (mx) + n/x] ψn (x) − ψn−1 (x) [mDn (mx) + n/x] ξn (x) − ξn−1 (x) (3.120) 0 0 For eliminating ψn and ξn the reccurence relations were used 0 ψn = ψn−1 (x) − nψn−1 (x) , x 0 ξn = ξn−1 (x) − nξn−1 (x) x (3.121) The logarithmic derivative satisfies Dn (mx), from the properties of spherical Bessel, the recurrence relation 1 n (3.122) Dn−1 = − ρ Dn + n/ρ and it can be calculated with downward recurrence. Also ψn and ξn satisfy ψn+1 (x) 2n + 1 ψn − ψn−1 (x) x (3.123) Now to calculate ψn , ξn = ψn − jξn by using upward recurrence with starting functions ψ−1 (x) = cos x, ψ0 (x) = sin x (3.124) ξ−1 (x) = − sin x, ξ0 (x) = cos x For speeding up the calculation a stop–criterion can be used, the whole process will be stopped when Nstop terms are calculated. Where Nstop is the integer closest to [58] Nstop = x + 4x1/3 + 2 (3.125) 3-7 Mie Theory for Biomedical Optics 45 Perhaps the best known program for computing Mie scattering coefficients is that by Bohren and Huffman, called BHMIE [54]. Although BHMIE is one of the earliest programs for Mie theory, it has a wide distribution and is considered simple, efficient and easy to modify. 3-7 Mie Theory for Biomedical Optics The interaction between electromagnetic waves and tissue is important for the development of diagnostic and therapeutic applications of light in medicine. To better understand the interaction of light within tissue it is useful to have a theoretical model from which the tissue optical properties can be derived. By considering cellular organelles of biological tissue as spheroidal scatterers whose interactions with light are governed by Mie theory, optical properties such as refractive index, scatterer size and distribution can be derived [52, 53]. The most relevant for OCT imaging from Mie theory, is the relationship between backscattering intensity and illuminating wavelength. Figure 3-4.1 suggests that as particle size increases there will be decreased backscattering, meaning that smaller scattering particles in biological tissue will produce most of the OCT signal. Chapter 4 Spectroscopic OCT 4-1 Introduction As described at Chapter 2 OCT images are generated by analyzing the envelope of the demodulated interference signal to produce two-dimensional cross-sectional images. However a great deal of information in the backscattered signal is not utilize with traditional OCT systems. In addition, two tissues with the same amount of backscattered intensity cannot be differentiate, even if those differ in cellular and subcellular structure. To resolve this problem other methods can been used for analyzing the backscatter signal such as spectroscopic analysis methods. For example, different types of tissue will have different absorption and scattering spectra depending on the cell sizes, blood content, water content and whether the area is oxygenated or deoxygenated. An extension of OCT is the Spectroscopic OCT (SOCT) for performing both cross-sectional tomographic and imaging of the spectral content. SOCT may find applications in functional imaging by detecting variations in blood oxygenation, early detection of cancer by detecting variations in cell size and nuclear density and for the detection of other pathologies by detecting changes in spectroscopic properties of tissue types not visible by traditional OCT. The first demonstration of SOCT had used the spectral centroid shift as the indicator of spectral modification to enhanced the contrast of OCT images [9, 11]. SOCT rapidly become a powerful extension of OCT with many applications [10, 6, 59] and it has been demonstrated that SOCT could be combined with LSS [50, 60] to eliminate the diffuse scattering background. As mentioned in Chapter 3 the size of the scatterers be determined from the intensity of the scattered light as a function of wavelength[50, 61], as well as from measurements of the scattering as a function of angle [51, 12]. 4-2 Mie theory in SOCT 4-2 47 Mie theory in SOCT As discussed in Chapter 3, depending on the scatterer size, the spectral scattering can be divided into three regimes. For particles much smaller compared to the wavelength, the spectral scattering is governed by the Rayleigh scattering. For particles much larger than the wavelength, the solution of spectral scattering can be approximated by geometric optics. For particles comparable to the wavelength, the spectral scattering can be solved using Mie theory. The most relevant process in OCT is Mie theory because of the wavelength emission of OCT sources which is at near–infrared spectra (1300 nm) and the dysplastic alterations which are of our interest are in the same scale. When the scatterer size is comparable to the wavelength, there is no simple means to solve for the scattering contribution, other than by the formal solutions of Maxwells equations and applying appropriate boundary equations. These calculations, collectively called Mie theory, dictate that the scattered wave for incident plane waves depends on the distribution of the refractive index of the scatterers, the incident wave frequency, and the scattering angle [55]. Mie theory is highly spectrally dependent, often forming characteristic modulation patterns. Figure 4-2 shows the characteristic difference of backscattered intensity for scatterers with different size. The backscattered intensity calculations are based on the Fortran subroutine BHMIE [54] which is described at Chapter 3-6, BHMIE have been modified and convert in Matlab source code in order to have uniformly sources code. The results for the refractive index of the tissue phantoms from section 4-5, and our source characteristics were used in the calculations. Because of the relative narrow bandwidth of our source, modulation appears only for larger scatterer. However, spectral differences do exist even for smaller scatterers. By quantifying the degree of spectral modulation in the backscattered spectrum information about the size of the scattering particles can be obtained. This information was used as contrast modality for providing enhanced differentiation in areas where the scattering particles sizes varies significantly. 4-3 Speckle As mentioned already, OCT has micrometer-scale axial and lateral resolution, so in the imaging volume of an OCT image many individual scattering particles exists simultaneously, such as mitochondria and nuclei. The existence of multiple scatterers in the imaging volume of the OCT gives rise to speckle patterns. These patterns are created by random interference of partial waves scattered by the scatterers. With interference, stochastic random phase shifts occur between the waves which result in statistical properties of the amplitude, phase, and intensity of speckle-modulated 4-3 Speckle 48 scattered fields. In addition, the spectral contents of the backscattered signal is altered due to the size effects of these scatterers [62]. Speckle patterns formed by tissue scattering are often called biospeckles. The possibility of obtaining information about structure and dynamic properties of tissues by using statistical or correlation analysis of biospeckles have been studied extensively in many areas [63, 64, 65]. Speckle is an unresovable signal and its properties depend on the size and the distribution of scatterers i.e. concentration, spacing and periodicity. In SOCT, speckle appears in both the intensity of the backscattered light and the modulation patterns of the local spectra. The modulation can be considered as an outcome of a stochastic process where the properties of the process are dependent on the size and distribution of the scatterers within the imaging volume. By analyzing the statistical properties of the backscattered spectrum one can extract information about the scattering particles in the imaging volume of OCT. −4 8 x 10 −4 1.2 1.15 Backscattered Intensity (A.U.) 7 Backscattered Intensity (A.U.) x 10 6 5 4 1.1 1.05 1 0.95 0.9 3 0.85 2 1.22 1.23 1.24 1.25 1.26 Wavelength (µ m) 1.27 1.28 0.8 1.22 1.29 1.23 1.24 1.25 1.26 Wavelength (µ m) −6 x 10 (a) 1.27 1.28 1.29 (b) −6 9 x 10 Backscattered Intensity (A.U.) 8 7 6 5 4 3 1.22 1.23 1.24 1.25 1.26 Wavelength (µ m) 1.27 1.28 −6 x 10 1.29 −6 x 10 (c) Figure 4.1: Example of back-scattered intensity. (a) Back-scattered intensity for 1 µm scatterer. (b) Back-scattered intensity for 2 µm scatterer. (c) Back-scattered intensity for 4 µm scatterer. 4-4 SOCT Instrumentation 49 Statistical properties of speckle can be divided into statistics of the first and second order. Statistics of the first order describe the properties of speckle fields at each point. Such description employs the intensity probability density function ρ(I) which is represented as a negative exponential function I 1 exp − ρ(I) = hIi hIi (4.1) This expression is valid for fully developed speckles and when the scattering amplitude follows gaussian statistics. Statistics of the second order show how fast the intensity changes from point to point in the speckle pattern and they can characterize the size and the distribution of speckle in the pattern. Goodman [66] and Goldfischer [67] were the first that use the power spectrum density (PSD) and autocorrelation analysis for studying the statistics of the second order. The correlation of intensity for two different points is (x1 , y1 ) and (x2 , y2 ) is rxx (x, y) = E {I(x1 , y1 )I(x2 , y2 )} (4.2) and its Fourier transform represents the power spectrum of a stochastic process. By analyzing the power spectrum statistical properties diagnostic useful information can be extracted. 4-4 SOCT Instrumentation Both standard TDOCT and FDOCT instrumentation can be used for SOCT. For the purpose of this study, a fiber-based TDOCT system with a broad bandwidth source was used, Figure 4.2 shows the schematic of the OCT system. The system uses a broadband superluminescent diodes (Superlum Broadlighter 1300), with a center wavelength of 1300 nm and a bandwidth of 55 nm. Resulting an axial resolution of 13.5 µm and lateral resolution of 25.6 µm. The interfering signal and reference light was detected using a New Focus Model 2011 photoreceiver detector. The interference fringes are acquired without demodulation using a 16-bit A/D card (National Instruments, PCI-6251) and the signal was digitized at 6x the carrier frequency. 4-4.1 Superluminescent diodes (SLDs) As described in Section 2-3, the laser source spectrum and power are important factors in determining the OCT resolution and sensitivity. In SOCT, this is especially important because SOCT uses the broad-band laser spectra to perform 4-5 Tissue Phantoms 50 spectroscopic analysis. The spectral features to be determined must lie within the laser source spectrum. At present, the most popular light sources in OCT are the Superluminescent diodes (SLDs). SLDs are optoelectronic semiconductor devices which are emitting broadband optical radiation based on superluminescence. Their structure and operation is similar to the edge-emitting laser diodes (EELD), containing an electrically driven p-n junction and an optical waveguide, but they lack an optical resonator, thus no laser action can occur. Optical resonators are suppressed by tilting the facets relative to the waveguide and can be suppressed even further with anti-reflection coatings. Essentially, an SLD is a semiconductor optical amplifier with no input signal. Depending on the material and structure, SLDs have different center wavelengths and bandwidths. The broadband SLD source that used for this thesis was developed by Superlum Diodes, Ltd., and consists of two single-mode fiber coupled SLD modules with slightly shifted central wavelengths. The first module has emission wavelength of 1285.5 nm with a bandwidth of 57.4 nm and the second module has emission wavelength of 1285.1 nm with a bandwidth of 55.3 nm. These emissions are combined by appropriate broadband singlemode fiber couplers to give a centered wavelength of 1300 nm and a bandwidth of 55 nm. 4-5 Tissue Phantoms For the purpose of this study solid tissue phantoms were made using polystyrene sphere solutions (Polybead Microspheres) of diameter 1 µm, 2 µm and 4 µm, and with a refractive index n = 1.59, embedded in an acrylamide gel. The imaging volume of the OCT system was approximately 30 µm x 30 µm x 15 µm. For reference mirror SLD 50/50 Beam Splitter PC D photoreceiver sample Figure 4.2: Schematic of the Time Domain OCT system that we used. 4-5 Tissue Phantoms 51 Table 4.1: Recipes for tissue phantoms (acrylamide gel) of different imaging volume concentration Microspheres diameter Concentration (Imaging Volume) 1 µm 2 µm 4 µm 50 spheres 5 spheres 2 spheres dH2 O (µL) 82.5 684 375 Polystyrene Microspheres (µL) 667.5 66 375 30% acrylamide (µL) 250 250 250 10% APS (µL) 20 20 20 TEMED (µL) 20 20 20 the 1 µm phantom the concentration was 50 spheres per imaging volume, for the 2 µm phantom 5 spheres per imaging volume and for the 4 µm 2 spheres per imaging volume. These phantoms were selected because they result in samples with similar backscattering coefficient and have enough scatterers in the imaging volume to create speckle modulation. An acrylamide gel is a separation matrix used in electrophoresis of biomolecules, such as proteins or DNA fragments. The following steps must be followed for the production of the phantoms: • Determine the appropriate gel composition and microspheres concentration(Table 4.1) for a given experiment. • Combine all reagents (except TEMED) in the order listed. • Add TEMED only when completely ready for polymerization to occur! • Allow gel to polymerize (∼ 2min) As mentioned in Chapter 2 OCT measures the group delay imposed by the sample, (Equation 2.45), if the thickness of the sample z is known the group index can be calculated from the group delay. By placing the sample on top of a planar reflecting surface and acquiring an OCT image, the refractive index of the sample 4-5 Tissue Phantoms 52 can be determined. The refractive index of the sample is defined as [68]: n= z0 + z z (4.3) where z 0 is the additional optical path length. From such a calculation the refractive index of the phantom was found to be n = 1.47. Figure 4.3: OCT image of a piece of the phantom placed on an unpolished metal substrate. The two vertical bars represent z, z 0 , from top to bottom. Chapter 5 Spectral Analysis of OCT Signals 5-1 Introduction In SOCT, the information on the spectral content of backscattered light is obtained by the time-frequency analysis of the interferometric OCT signal. The backscattered spectrum can be acquired over the entire available optical bandwidth in a single A-scan, allowing the spectroscopic information to be analyzed in a depthresolved way [69]. In the literature, the short-time Fourier transform (STFT) and the continuous wavelet transform (Morlet transform) have been used for obtaining the backscattering spectrum. In both of these techniques, performance is complicated by the time-frequency uncertainty principle, which states that there exists an inherent trade-off between the spectral resolution and the time resolution. Improvement in one implies degradation in the other. In our case, high spatial resolution is required because spectral back-scattering is a short-range effect in that large spectral variations can happen within submicrometer scale distance (cell or tissue boundaries). From the work done in LSS area there are currently two approaches for sizing the scatterers based on the measured spectra. The first approach is based on pitch detection with the use of Fourier transform or determining the autocorrelation of the transform. The principle behind the first approach is that the oscillation frequency in the wavelength-dependent scattering is size dependent, such that larger scatterers tend to produce more oscillatory patterns [45]. The second approach is based on curve fitting using least-square or χ2 methods [12] using Mie theory to fit the normalized experimental measurement to the theoretical predicted. The scope of this thesis is to introduce a novel spectral analysis method for SOCT signals. It is known from previous work in the SOCT area that the spectral features can be indicators of scatterer size by using spectral analysis methods such as the Fourier transform or the autocorrelation [11, 60] There are many kinds of spectral analysis methods, including Fast Fourier Transformation (FFT) method, 5-2 Spectral Analysis Based on Fourier Transformation 54 Yule-Walker method, Burg method, Least Squares method and Maximum likelihood method. The Burg method was explored over other methods because it: • Offers high resolution • Converge faster for shorter segments • Is computationally more efficient than other spectral techniques. In this chapter the methods that were used for spectral analysis of the OCT signals, and the methods for statistical multivariate analysis will be described. 5-2 Spectral Analysis Based on Fourier Transformation The original or “classical” methods for spectrum estimation are based directly on the Fourier transform and were used in the early 1950s. These methods gained additional popularity with the development of the fast Fourier transform (FFT) in the mid-1960s. In spite of development, of newer, more “modern” techniques, the classical methods are still preferred for long and stationary data. 5-2.1 Energy Spectrum Density (ESD) The Spectral Density of a sampled signal or time series x(n), −∞ < n < ∞ is a positive real function of a frequency variable associated with a stationary stochastic process, or a deterministic function of time, which has dimensions of power per Hz, or energy per Hz. The Energy Spectrum Density (ESD) describes how the energy (or variance) is distributed with frequency and is defined by the module square of its Fourier transform. The Fourier transform of the sequence x(n) is X(ω) = ∞ X x(n)exp(−jωn) (5.1) x(n)exp(−j2πf n) (5.2) n=−∞ or, equivalently X(f ) = ∞ X n=−∞ The ESD is defined ∞ X 2 Sxx (ω) = |X(ω)| = X(ω)X (ω) = x(n)exp(−jωn) 2 ∗ n=−∞ (5.3) 5-2 Spectral Analysis Based on Fourier Transformation 55 The autocorrelation function is defined by rxx (k) = ∞ X x∗ (n)x(n + k) (5.4) n=−∞ The Fourier transform of the autocorrelation function with the use of WienerKhintchine theorem ∞ X Sxx (ω) = rxx (k)exp(−jkωn) (5.5) n=−∞ Hence the ESD also can be obtained by the Fourier transform of the autocorrelation. From the relations above there are two different methods for computing the ESD. The first method is the direct method which involves computing the Fourier transform of x(n) and then the square power of it to obtain Sxx (ω). The second method is called the indirect method because it requires two steps. First the computation of autocorrelation rxx (k) and then the Fourier transform of the autocorrelation is computed as in Eq. 5.5 to obtain the ESD. In practise, only the finite-duration sequence x (ns ), 0 ≤ ns ≤ N − 1 is the total number of data samples for computing the spectrum of the signal. In effect, limiting the duration of the sequence is equivalent to multiplying by a rectangular window. Thus we have  x(n ) 0 ≤ n ≤ N − 1 s s (5.6) x̃(ns ) = x(n)w(n) = 0 otherwise The ESD of the windowed sequence x̃(ns ) is given by −1 N 2 X Sx̃x̃ (f ) = |X̃(f )| = x̃(n)exp(−jωn) 2 (5.7) ns =0 The spectrum given by Eq. 5.7 can be computed numerically from the Discrete Fourier Transform (DFT) of N points [70]. 5-2.2 Power Spectrum Density (PSD) The SOCT signals due to speckle, as we mention at Chapter 4-3, are stochastic process and such signals have finite energy and are characterized by a Power Spectrum Density (PSD). Lets define the autocorrelation function of a stationary stochastic process x(t) γxx (τ ) = E {x∗ (t)x(t + τ )} (5.8) 5-2 Spectral Analysis Based on Fourier Transformation 56 where E is defined as the mean operator. The autocorrelation estimation for the sampled sequence x(n) of the signal is 1 rxx (m) = N 1 rxx (m) = N N −m−1 X n=0 N −1 X x∗ (n)x(n + m) 0≤m≤N −1 (5.9) x∗ (n)x(n + m) m = −1, −2, . . . , 1 − N n=|m| With the use of Wiener–Khintchine theorem we obtain the PSD Pxx (ω) = N −1 X rxx (m)exp(−jωm) (5.10) m=−(N −1) By inserting 5.9 into Equation 5.10 we have Pxx (ω) = N −1 2 1 X 1 x(n)exp(−jωn) = |X(ω)|2 N n=0 N (5.11) This form of the PSD is defined as the Periodogram and it is popular for spectrum estimation because the computation is especially convenient. 5-2.3 Computation using the FFT As given by Equations 5.7 and 5.11 the estimated ESD Sxx (ω) and the periodogram Pxx (ω) respectively can be computed by the use of the DFT. The DFT is efficiently computed by Fast Fourier Transform (FFT) algorithm. However if the data segment consists of N points, then an N -point FFT produces only N samples of the corresponding Fourier transform. This computation does not provide a very good representation of the spectrum, to overcome this the Fourier transform can be evaluated at a larger and more closely spaced frequency values by “zero padding” the data sequence and using a larger FFT. Zero-padding does not change the shape of the spectrum, it only provides a way to evaluate the spectrum at a more closely spaced set of frequency values. Spectral analysis based on Fourier Transformation provides a simple, reliable and efficient way for obtaining the spectrum. It requires only two computational steps function and then with the use of FFT the spectrum can be obtained. The major disadvantage of this method for spectral estimation is the limited resolution, i.e. the limited ability to distinguish closely spaced features of the spectrum. 5-3 Spectral Analysis Based on Burg’s Method 5-3 57 Spectral Analysis Based on Burg’s Method The non-parametric methods described above make no assumption about how the data were generated and the estimation is based entirely on a finite record of data. The assumption in Equation 5.10 that the autocorrelation estimate rxx is zero for m ≤ N severely limits the frequency resolution and the quality of the estimated PSD. The parametric or model–based methods of spectral estimation do not require such assumptions and in fact Burg’s method bypasses any estimation of the autocorrelation function. Parametric methods for rational spectra and Burg’s method for AR spectrum parameter estimation are discussed below. AR spectrum parameter estimation has been used in data forecasting, speech coding and recognition, model-based spectral analysis, model-based interpolation, signal restoration. Also it has been used for ultrasonic tissue characterization [71, 72]. 5-3.1 Rational Power Spectra The power spectrum density of a stochastic process could be expressed as a rational function 2 2 B(ω) (5.12) Pxx (ω) = σ A(ω) where σ 2 is a positive scalar, and the polynomials A(ω) and B(ω) are A(ω) = 1 + q X αk exp(−jkω) k=1 B(ω) = p X (5.13) bk exp(−jkω) k=0 This function can similarly be expressed in the z–domain φ(z) = ∗ ∗ 2 B(z)B (1/z ) σ A(z)A∗ (1/z ∗ ) (5.14) where the polynomials A(z) and B(z) have roots that fall inside the unit circle in the z–plane. The rational PSD can be associated with a signal obtained by filtering white noise of power σ 2 with transfer function H(ω) = H(z)|z=exp(jω = B(z)/A(z) [73] The filtering gives us a relation between the PSD as a signal x(n) with the white noise w(n) B(p) x(n) = w(n) (5.15) A(q) It can be transformed into a difference equation, from where three specific cases 5-3 Spectral Analysis Based on Burg’s Method 58 can be separated x(n) + p X αk x(n − k) = k=1 q X bk w(n − k) (5.16) k=0 1. Autoregressive (AR) process. Where b0 = 1, bk = 0, k > 0 resulting a linear, all-pole filter H(z) = 1/A(z) and the difference equation x(n) + p X αk x(n − k) = w(n) (5.17) |b0 |2 |A(ω)|2 (5.18) k=1 The PSD for AR model is AR Pxx (ω) = For the AR model the constant |b0 |2 can be replaced by the error variance σP2 in the PSD giving σP2 AR (5.19) Pxx (ω) = |A(ω)|2 2. Moving Average (MA) process. Where αk = 0, k ≤ 1 resulting a linear, all-zero filter H(z) = B(z) and the relationship below x(n) = q X bk w(n − k) (5.20) k=0 The PSD for MA model is MA Pxx (ω) = |B(ω)|2 (5.21) 3. Autoregressive Moving Average (ARMA) process. In this case the linear filter H(z) = B(z)/A(z) has both finite poles and zeros in the z –plane and the corresponding difference equation is given by Equation 5.16. The PSD for ARMA model is |B(ω)|2 ARM A (5.22) Pxx (ω) = |A(ω)|2 5-3.2 Burg’s Method It is obvious from the relations above that the estimation of the ARMA parameters, ak and bk is essential for the estimation of the PSD. Burg devised a method for estimating the AR parameters as an order–recursive least square lattice method [74]. The AR parameters with Burg’s method can be directly estimated from the data without the intermediate step of computing a correlation matrix and solving Yule-Walker equations, like other methods. Burg’s method is based on the minimization of the forward and backward in linear errors with the constraint that the AR parameters satisfy the Levinson-Durbin recursion. 5-3 Spectral Analysis Based on Burg’s Method 59 Assume we have data measurements x(n), n = 1, 2, . . . , N , we define the forward and backward prediction errors for a pth–order model as êf,p (n) = x(n) + m X α̂p,k x(n − k) t = p + 1, . . . , N (5.23) k=1 êb,p (n) = x(n − p) + m X ∗ α̂p,k x(n + k − m) t = p + 1, . . . , N (5.24) k=1 where the AR parameters α̂p,k are related to the reflection coefficients K̂p with the constraint that they satisfy the Levinson-Durbin recursion [? ] given by α̂p,k =  α̂ p−1,k ∗ , i = 1, . . . , p − 1 + K̂p α̂p−1,p−i k̂ , p (5.25) i=p The next step in Burg’s method for estimating the AR parameters is to find the reflection coefficients K̂p that minimize the least–squares error h i f b Em = min Êm (p) + Êm (p) k where f Êm (p) = N X |êf,p (k)|2 k=p+1 b Êm (p) = N X (5.26) (5.27) |êb,p (k)|2 k=p+1 Also the prediction errors satisfy the following recursive êf,p (n) = êf,p−1 (n) + K̂p ê∗b,p−1 (n − 1) êb,p (n) = êb,p−1 (n − 1) + K̂p ê∗f,p−1 (n) (5.28) Inserting Equation 5.28 in Equation 5.25 and performing minimization of Em with respect to the reflection coefficients K̂m results in N X −2 K̂m = êf,p−1 (n) ê∗b,p−1 (n − 1) k=p+1 N X (5.29) |êf,p−1 (n)|2 + |êb,p−1 (n − 1)|2 k=p+1 The denominator is the least-squares estimate of the forward and backward errors 5-4 Statistical Multivariate Analysis 60 f b Êm−1 and Êm−1 respectively. Thus −2 K̂m = N X êf,p−1(n) ê∗b,p−1 (n − 1) k=p+1 h i f b Êm−1 + Êm−1 (5.30) f b where Êm−1 + Êm−1 is an estimate of the total error Em . A recursion could be developed for estimation the total least square error Em = (1 − |K̂m |2 )Em−1 − |êf,p−1 (m − 1)|2 − |êb,p−1 (m − 2)|2 (5.31) To summarize, the Burg’s method estimates the reflections coefficients from Equations 5.30 and 5.31 and the Levinson-Durbin algorithm is used to obtain the AR model parameters α̂(k). From Equation 5.19 and the estimates of the AR parameters we form the PSD Êp Bu P̂xx (ω) = p 2 X 1 + α̂ (k)exp(−jωk) p (5.32) k=1 5-4 Statistical Multivariate Analysis The statistical analysis of the spectra obtained from the methods that described above is essential for scatterer size estimation and for the classification. Backscattered OCT spectra are multivariate functions of wavelength. An algorithm for studying such spectra should use multivariate statistical analysis. Advanced analysis techniques, such as Principal Component Analysis (PCA) and Multivariate Analysis of Variance (MANOVA), were used for providing more insight into the spectral changes. PCA is used as a dimension reducing technique and for extracting features from the training set to be used for size estimation and for classification. MANOVA is used for discriminant analysis and classification. 5-4.1 Principal Component Analysis (PCA) Principal component analysis (PCA) is a method of statistical analysis useful in data reduction and interpretation of multivariate data sets [75]. This is achieved by transforming to a new set of variables, the principal components (PCs), which are mutually-orthogonal linear combinations and are order based on the variance of the original variables. PCs is a smaller data set with less redundancy that give as a very good representation of the original data set and this makes PCA a powerful and versatile analysis method. 5-4 Statistical Multivariate Analysis 61 The starting point for PCA is a random vector x with n elements, and x has zero empirical mean, is centered by subtracting its mean. A linear combination of the vector x can be stated y1 = n X wk1 xk = w1T x (5.33) k=1 where w11 , . . . , wn1 are elements of an n–dimensional weight vector w1 . If y1 has maximum variance then is the first PC of x, variance depends on both the norm and orientation of the weight vector w1 the constraint that the norm equals to 1 must be imposed, kw1 k = 1. The variance of y1 is defined as E{y12 } = E{(w1T x)2 } = w1T E{xxT }w1 = w1T Cx w1 (5.34) where Cx is the m x n covariance matrix of x. The weight vector that maximizes Equation 5.34 must be calculated so that kw1 k = 1 , it is well known that the eigenvectors of the covariance matrix Cx , e1 , . . . , en are the solutions for the maximization of variance [76]. Thus the first PC is given by y1 = eT1 x (5.35) Generalized Equation 5.34 to k PCs, yk = wkT x one can find the rest PCs under the constraint that yk is uncorrelated with all the previously found PCs. It follows that wk = ek (5.36) Thus the kth PC is yk = eTk x (5.37) It have been showed that the PC basis vector wk are eigenvectors ek of the covariance matrix Cx , it follows that 2 E{ym } = eTm E{xxT }em = eTm Cx em = dm (5.38) where dm are the eigenvalues of Cx . Thus by ordering the eigenvectors found from the covariance matrix by eigenvalue, from highest to lowest, this gives PCs in order of significance. A very important practical problem is to choosing the number of PCs, m in Equation 5.38. There is a trade-off between error and the amount of data needed because sometimes a rather small number of PCs are sufficient. 5-4 Statistical Multivariate Analysis 5-4.2 62 Multivariate Analysis of Variance (MANOVA) Multivariate Analysis of Variance (MANOVA) is used to obtain new linear combinations of variables with maximum separation between categories. The data in MANOVA may be regarded as forming a matrix X in which each row corresponds to an object nj and each column corresponds to a measured variable. X is an m x n matrix of data values and each row is a vector of measurements on n variables for a single observation. We have performed a one-way MANOVA for comparing the multivariate means of the columns of X, grouped by group. Group is a grouping variable defined as the size array in our case, two observations are in the same group if they have the same value in the group array. The MANOVA test makes the following assumptions about the data in X: • The populations for each group are normally distributed. • The variance-covariance matrix is the same for each population. • All observations are mutually independent. 5-4.3 Classification A subject closely related to MANOVA is that of classification and discriminant analysis. A classification algorithm is used to determine in which category each sample belongs. For this classification, a discriminant quadratic type function can be used which fits a multivariate normal density to each group, with covariance estimates stratified by group. From the discriminated data set we can compute the sensitivity and the specificity of our classification. Sensitivity is defined as sensitivity = number of True Positives number of True Positives + number of False Negatives (5.39) and in diagnostic methods tell us what percentage of the data set have been recognized with the disease. Specificity is defined as specificity = number of True Negatives number of True Negatives + number of False Positives (5.40) and in diagnostic methods tell us what percentage of the data set have been recognized without the disease. Chapter 6 Results 6-1 Introduction As described at chapter 4-4 a fiber optic Michelson interferometer was used to measure the relative optical path difference between a reference arm and the phantoms tissues layers at the sample arm 4.2. By mechanically varying the path length in the reference arm with a scanning galvanometer an interference fringe is obtained for an arbitrary path length in the sample. To generate a single Axial scan (A-scan) in the image, an optical beam is incident on the sample at a single transverse location while the reference arm is scanned. Each A-scan resembles a high frequency carrier, amplitute modulated with a low frequency signal. The carrier signal contains all the spectroscopic information of the sample, while the modulation contains information about the scattering structure. For generating a 2 − d image (B–scan), the beam is translated in a transverse direction over the sample. As mentioned before, our OCT system has an imaging volume approximately 30 µm x 30 µm x 15 µm, and the phantoms enough scatterers in the imaging volume for creating speckle modulated patterns. Speckle is essential for our spectral analysis method. For each phantom 200 A-scans were acquired with the first 100 A-scans used as training set and the rest 100 as sample set. Axial scans were sampled at 6 x the carrier frequency. Collected data were analyzed using Matlab. 6-2 Spectra Calculation Following the acquisition, preprocessing the obtained data begun with the normalazition of the Root Mean Square (RMS) value to unity. This removed the effect of intensity differences between scans and samples. Subsequently, 100 scans were used as a training set and the remaining as a sample set. Average spectra for the training sample were obtained using both methods described in Chapter 5. The Fourier transform based method can be summarized as follows: 6-2 Spectra Calculation 64 1. Take the Fourier transform of the OCT intensity-based image data matrix to generate the backscattered spectrum 2. Take the autocorrelation of the backscattering spectra The Burg’s based method can be summarized as follows: 1. Reshape OCT intensity-based image data matrix 2. Use Burg’s algorithm to obtained an AR-parameter estimate of the Power Spectral Density (PSD) of the reshaped matrix and the corresponding frequencies The Fourier transform based method, as expected, was more noisy and with limited resolution, eventhough spectral differences can be seen in the spectra from different phantoms. The full width magnitude around 75% is an indicator of the scatterer size (Figure 6-2), a feature exploited by others in LSS [45, 46]. Burg’s method results in characteristic spectral differences with much greater spectral resolution. Figure 6-2 we can noticed the different tilt for each phantom which is predicted by Mie theory. There is a significant amount of spectral modulation due to the random positioning of the scatterers inside the imaging volume, which makes difficult to distinguish their scattering pattern. Theoretical studies have showned that spectral analysis is possible with the assumption that the scattering from different locations has the same general wavelength-dependent scattering profile [61]. Biologically this is true, epithelium tissue demonstrates layered or regional structure where adjacent scatterers are more or less homogeneous. Also experimental observations agree that is extremely difficult to distinguish the wavelength-dependent scattering pattern based on only one SOCT measurement [11]. One simple method to resolve this problem is to average the OCT signal around the scan of interest before obtaining the backscattered spectrum. A sliding window was used for averaging the scans adjacent to the scan of interest. For spectral analysis a rectangular window of the OCT image for each phantom was used with 3001(axial) x 25(transverse) pixel dimensions. Following the averaging each spectrum was normalized to the system spectrum. Although not necessary for the analysis, the normalization accentuates the differences between the spectra which makes studying the spectral variations easier. Also for the Fourier transform based method, median filtering was applied in an effort to reduce the effects of the high level of noise present. 6-2 Spectra Calculation 65 Normalized ACF 1 1 um 2 um 4 um 0.9 0.8 Ampl 0.7 0.6 0.5 0.4 0.3 0.2 1.3 1.305 1.31 lag 1.315 1.32 5 x 10 Figure 6.1: The autocorrelation of the backscattering spectra obtained with FFT Normalized Average Training Spectra 1 1 um 2 um 0.9 4 um 0.8 0.7 Ampl 0.6 0.5 0.4 0.3 0.2 0.1 0 3.25 3.3 3.35 3.4 3.45 3.5 3.55 frequency(kHz) 3.6 3.65 3.7 3.75 4 x 10 Figure 6.2: Back-scattered normalized average power spectra obtained with Burg’s method 6-3 Spectral Analysis 6-3 66 Spectral Analysis The statistical analysis of the spectra of the above samples begins with a reduction of the number of variables per sample. The reduction is achieved using Principal Component Analysis (PCA), PCA can identifying patterns in data, and expressing the data in such a way as to highlight their similarities and differences. All the training groups for each phantom were merged to form a new training group data ˆ tr (AllP xx ) for PCA, where each column corresponds to the training data from each phantom. Then a so-called Feature Vector (FV) is constructed by their Principal Components (PCs), FV is constructed by taking the first n PCs and forming a matrix with these PCs in the columns FV = (P C1 P C2 . . . P Cn ) (6.1) FV with the first 35 PCs describes more than 99.99% of the training data group variance. To obtain a new orthogonal basis for both the data groups with no redundant information, the FV can be used by simply left multiplying both group data. P̂PxxCA tr = AllPtr (6.2) xx FV The new transformed data have been expressed in terms of the PCs in FV and the principal differences of the PCs between each phantom will be exploited for scatterer size estimation and classification. A classification scheme followed to determine in which category each sample belongs. First one-way Multivariate Analysis of Variance (MANOVA) was applied to the new training group P̂PxxCA tr to obtain new linear combinations of variables. For comparing the multivariate means of the new training group P̂PxxCA tr a matrix label as size matrix (d̂) was constructed and each column of d̂ is the size of each phantom. Size matrix d̂ in MANOVA is defined as a categorical variable for grouping the new training data group. MANOVA have resulted in two eigenvectors on which the data must be projected. A discriminant quadratic type function can then be used which fits a multivariate normal density to each group, with covariance estimates stratified by group. From the discriminated data set, the sensitivity and the specificity of our classification can be computed. In addition to the classification scheme, an estimate of the diameter of the microspheres was calculated. A linear dependence was assumed between particle diameter and frequency and the new training data group P̂PxxCA tr were used to give solution to the set of linear equations Â = P̂PxxCA tr −1 d̂ (6.3) 6-3 Spectral Analysis 67 Then coefficient matrix A can be used for scatterer size estimation with sample training group (6.4) d̂ = P̂PsaCA Â The success of the algorithm can be assessed by evaluating the mean error and the standard deviation for all estimates. Therefore, by studying the mean error and the classification results, the optimum settings for both techniques can be found. Figure 6.3(a) shows the relation between the mean error estimate for the scatterer size versus the parameters p for the AR model, there is no obvious relation between the mean erron and the AR parameters N Burg. The mean error for the size estimation is minimized for AR parameters N Burg = 120. Also, the classifications results Figure 6.3(b) versus the AR parameters have the same behaviour and the best classification results is for AR parameters N Burg = 120. The number of PCs for the construction FV also affect the results, Figures 6.3(c)-(d) show mean error and classification results for different numbers of PCs, for both cases the best results are for 35 PCs. The same study was made for the Fourier based method, the number points of the FFT (N F F T ) and the number of PCs were examined. From Figures 6.4(a)-(d), again 35 PCs are giving the best results and the points of the FFT are N F F T = 4096 = 212 . The results from the whole process have been more than promising for Burg’s method, has successfully classified the scatterers by category with sensitivity and specificity more than 85% (Figure 6.5) and the mean error for the size estimation was less than 17 %, (Table 6.1). Results from the Fourier based method, as expected were quite poor due to the low resolution and the high level of noise, (Table 6.2). A number of features were study, especially for the backscattered spectrum. For studying the relationship between scatterer size and frequency the square power and the derivative of the backscattered spectrum were used for PCA. Table 6.3 and Table 6.4 are the results for the square power and the derivative respectively.There is no improvement therefore a combination between the single power with the square tr power and the derivative. The dimension of matrix AllP̂xx is doubled, new columns are added for the square power and the derivative respectively. The results now are improve for the combination of single power and derivative (Table 6.5), the other combination results were satisfying. Figure 6.5 are the MANOVA results for the single power and the two combinations, single power with the derivative have exactly the same results. Because an approximative derivative was used, which essentially is the difference between adjacent elements of the single power of the spectrum. 6-3 Spectral Analysis 68 Table 6.1: Results for Burg’s Method with window 3001 x 25 pixels and p = 120 AR parameters D Concentration Sensitivity Specificity Mean Error St. Dev. (µm) Sph/I.V. (%) (%) (%) Error(%) 1 50 100 100 2 5 100 100 16.44 19.10 4 2 85 100 Table 6.2: Results for FFT/Autocorrelation with window 3001 x 25 pixels and N F F T = 212 D Concentration Sensitivity Specificity Mean Error St. Dev. (µm) Sph/I.V. (%) (%) (%) Error(%) 1 50 75 82 2 5 69 82 65.35 48.52 4 2 62 82 D (µm) 1 2 4 Table 6.3: Results for square power of the spectrum P̂Bu tr Concentration Sensitivity Specificity Mean Error St. Dev. Sph/I.V. (%) (%) (%) Error(%) 50 100 97.50 5 94 97.50 32.83 32.71 2 95 97.50 D (µm) 1 2 4 ˆ Bu Table 6.4: Results for derivative of the spectrum dP tr Concentration Sensitivity Specificity Mean Error St. Dev. Sph/I.V. (%) (%) (%) Error(%) 50 100 100 5 91 100 24.21 21.56 2 94 100 D (µm) 1 2 4 Table 6.5: Results for single power and derivative of P̂Bu tr Concentration Sensitivity Specificity Mean Error St. Dev. Sph/I.V. (%) (%) (%) Error(%) 50 100 100 5 100 100 15.79 18.31 2 85 100 Table 6.6: Results for single power and square power of P̂Bu tr D Concentration Sensitivity Specificity Mean Error St. Dev. (µm) Sph/I.V. (%) (%) (%) Error(%) 1 50 100 100 2 5 82 100 16.81 15.96 4 2 93 100 6-3 Spectral Analysis 69 1 um (50) 2 um (5) 4 um (2) Sensitivity Vs #NBurg Mean Error Vs #NBurg 40 110 100 90 30 Sensitivity (%) mean error (%) 35 25 80 70 20 60 15 50 20 40 60 80 100 120 140 160 20 40 60 80 # NBurg (a) 120 140 160 (b) 1um (50) 2 um (5) 4 um (2) Sensitivity Vs #PC Mean Error Vs #PC 28 100 # NBurg 110 26 105 100 Sensitivity (%) Sensitivity (%) 24 22 20 95 90 85 18 80 16 75 20 25 30 35 40 45 20 25 30 # PC 35 40 45 # PC (c) (d) Figure 6.3: Plots of mean error and sensitivity versus N Burg (a), (c) and principal components (b), (d) for Burg’s method Mean error Vs Nfft 1 μm 2 μm 4 μm Sensitivity Vs Nfft 90 68 80 70 66 Sensitivity (%) Mean error (%) 60 64 62 50 40 30 60 20 58 10 0 2000 4000 6000 8000 0 10000 12000 14000 16000 18000 2000 4000 (a) Sensitivity (%) Mean Error (%) 72 70 68 66 64 35 40 # PC (c) 10000 12000 14000 16000 18000 Sensitivity Vs #PC Mean Error Vs #PC 30 8000 (b) 74 25 6000 # NFFT # NFFT 45 50 1 um 2 um 4 um 76 74 72 70 68 66 64 62 60 58 56 54 52 50 48 46 44 42 25 30 35 40 45 50 # PC (d) Figure 6.4: Plots of mean error and sensitivity versus N F F T (a), (c) and principal components (b), (d) for FFT/Autocorrelation 6-3 Spectral Analysis 70 Sample Data Scatter Plot 50 Training Data Scatter Plot 50 1 2 4 40 1 2 4 40 MANOVA Eigenvec 1 30 MANOVA Eigenvec 1 30 20 10 20 10 0 0 -10 -10 -20 -25 -20 -25 -20 -15 -10 MANOVA Eigenvec 2 -5 -20 -15 -10 MANOVA Eigenvec 2 0 -5 0 (a) Training Data Scatter Plot 50 Sample Data Scatter Plot 1 2 4 40 50 1 2 4 40 30 MANOVA Eigenvec 1 MANOVA Eigenvec 1 30 20 10 20 10 0 0 -10 -10 -20 -25 -20 -15 -10 MANOVA Eigenvec 2 -5 -20 -25 0 -20 -15 -10 MANOVA Eigenvec 2 -5 0 (b) Training Data Scatter Plot Sample Data Scatter Plot -20 -20 1 2 4 -40 -60 MANOVA Eigenvec 1 MANOVA Eigenvec 1 -60 -80 -100 -80 -100 -120 -120 -140 -140 -160 1 2 4 -40 -160 0 5 10 15 MANOVA Eigenvec 2 20 25 0 5 10 15 MANOVA Eigenvec 2 20 (c) Figure 6.5: Results of the MANOVA analysis of 100 training and 100 sample spectra for the single power (a), the single power and the derivative (b), the single and square power (c). (The dark lines are the classification area borders resulting from the discriminant analysis) 25 6-4 Depth Analysis 6-4 71 Depth Analysis Previous studies on SOCT have used each pixel in the OCT image for calculating local spectra [9, 11]. In our approach a part of the OCT image was only used, a box window dimension of 3001(axial) x 25(transverse) pixel. By varying the axial initial position of the window, a significant differences to the acquired spectrum was noticed. Theoretical studies of the OCT signal have indicated that there is a depth dependency for the OCT signal using the small-angle approximation of the Radiative Transfer Equation (RTE) [77, 78] and the extended Huygens-Fresnel principle [79]. In the literature only one work refers to the depth-dependency of the SOCT spectrum by using theoretical studies based on Wigner distribution [80]. To verify the depth dependency for the SOCT spectra a number of OCT images were acquired from the 2 µm phantom. The first step was to acquire images for different focus locations, this can be achieved by varying the focus position of the OCT system, and three images were acquired with the focus, midway and low in the sample. Also three images were acquired by varying the position of the reference mirror, for obtaining images with different pathlengths. The spectra from the first OCT image where the focus was at the top of the sample are shown in Figure 6.6. Spectra were obtained from different depth positions inside OCT image, in focus (s1) and below focus (s2). The spectral differences indicate that, s2 is shifted and has different shape from s1. Depth analysis was continued for the image where the focus was in the middle of the sample. The corresponding spectra are s3, s4 and s5 for above, in and below focus (Figure 6.7). Again there are significant spectral differences and also the amplitute of spectra is different in this case. The third image was obtained with focus at the bottom of the sample, with s6, s7 and s8 taken above, in and below focus (Figure 6.8). For the images with different pathlengths the spectra also have different shape and they are shifted (Figure 6.9). Further analysis was done for comparing spectra from the OCT images. First, spectra from the same depth (s2, s4 and s6) were compared, again spectral differences such as shift and different shape were observed (Figure 6.10). Also the in focus spectra were compared (s1, s4 and s7), here the spectral differences are only for the shape of the spectrum (Figure 6.11). It is clear that there is a depth dependency in the SOCT signals. Temporal coherence have been suggested for explaining this phenomenon [80]. However, further study is required to understand what is happening since it is hard to decouple focus and pathlength dependencies. 6-4 Depth Analysis −8 7 72 Focus at the top of the sample x 10 focus (s1) below (s2) 6 5 4 3 2 1 0 24.5 25 25.5 26 Frequency (kHz) 26.5 27 27.5 Figure 6.6: Spectra from different depths with the focus at the top of the sample −9 8 Focus in the middle of the sample x 10 above s3 focus s4 below s5 7 6 5 4 3 2 1 0 24.5 25 25.5 26 26.5 Frequency (kHz) 27 27.5 Figure 6.7: Spectra from different depths with the focus at the middle of the sample 6-4 Depth Analysis −9 8 73 Focus at the bottom of the sample x 10 above s6 focus s7 below s8 7 6 5 4 3 2 1 0 24.5 25 25.5 26 Frequency (kHz) 26.5 27 27.5 Figure 6.8: Spectra from different depths with the focus at the bottom of the sample Spectra with same pathlength and different depth 1 long (l) medium (m) small (s) 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 24.5 25 25.5 26 26.5 Frequency (kHz) 27 27.5 Figure 6.9: Spectra from below the surface at different pathlengths 6-4 Depth Analysis 74 Spectra from the same depth 1 focus above (s2) in focus (s4) focus below (s6) 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 24.5 25 25.5 26 26.5 Frequency (kHz) 27 27.5 Figure 6.10: Spectra from the same depth from three different OCT images In Focus Spectra 1 top (s1) middle (s4) bottom (s7) 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 24.5 25 25.5 26 26.5 Frequency (kHz) 27 27.5 Figure 6.11: In focus spectra from three different OCT images Chapter 7 Summary and Future Work 7-1 Summary In this thesis a review was given for the background knowledge and important concepts of OCT, especially in the Time–Domain. A thorough study of Mie scattering theory and its applications in SOCT was given, a Matlab source code was developed for calculating backscattered Mie spectra. A brief description of speckle and its properties was given, and the prospect of SOCT. Relative small volume tissue phantoms with high microspheres concentration have bee constructed for imaging purposes. Spectral analysis method for OCT signals were reviewed, based on classic non–parametric methods such as Periodogram/FFT and based on autoregressive parametric methods such as Burg’s method. Based on the previous sections an autoregressive spectral estimation was suggested for acquiring the backscattered spectrum from the OCT signal. Then a PCA-based algorithm was used to extract diagnostic features and to reduce the dimension of the spectra. A classification scheme based on MANOVA followed to determine in which category each sample belongs. In addition to the classification scheme, an estimate of the diameter of the microspheres was calculated, based on the assumption that a linear dependence between scatterer size and frequency exists. 7-2 Future Work The technique developed in this thesis can result in an extremely valuable tool for the investigation of disease tissue features which now remain below the resolution of OCT. For this study a Time–Domain OCT system was used, implementation of this technique in Fourier–Domain OCT systems, required to enable clinical studies. FDOCT has higher resolution and high acquition rate for real time imaging. Clinical applications such as dissease imaging tissues will be a major step for OCT cancer studies. Also different imaging scenarios should be investigated such as tissue phan- 7-2 Future Work 76 toms with different concentration, to estimate the concentration in addition to the diameter of the phantom using a Mie based approach. Another issue that rises from this study is the depth dependency of the SOCT spectra, an issue that demands rigorous possibly analysis using joint Time–Frequency Distributions (jTFD). There are many other potential future SOCT research directions and application areas for this study. The additional information provided by SOCT increases our ability for tissue characterization, disease diagnosis, and other medical and biological investigations. Bibliography [1] D. Huang, E. Swanson, C.P. Lin, J.S. Schuman, W.G. Stinson, W. Chang, M.R. Hee, T. Flotte, K. Gregory, C.A. Puliafito, and J.G. Fujimoto. Optical Coherence Tomography. Science, 254(5035):1178–1181, 1991. 12, 15 [2] J. A. Izatt, M. R. Hee, E. A. Swanson, C. P. Lin, D. Huang, J. S. Schuman, C. A. Puliafito, and J. G. Fujimoto. Micrometer-scale resolution imaging of the anterior eye with optical coherence tomography. Arch. Ophthalmol., 112: 1584–1589, 1994. 13 [3] Wei Luo, Daniel L. Marks, Tyler S. Ralston, and Stephen A. Boppart. Threedimensional optical coherence tomography of the embryonic murine cardiovascular system. Journal of Biomedical Optics, 11(2):021014, 2006. 13 [4] J. Ik-Kyung, G. Tearney, B. MacNeill, M. Takano, F. Moselewski, N. Iftima, M. Shishkov, S. Houser, T. Aretz, E. Halpern, and B. Bouma. In Vivo Characterization of Coronary Atherosclerotic Plaque by Use of Optical Coherence Tomography. Circulation, 111(12):1551–1555, 2005. 13 [5] Wolfgang Drexler. Ultrahigh-resolution optical coherence tomography. Journal of Biomedical Optics, 9(1):47–74, 2004. 13 [6] Chenyang Xu, Jian Ye, Daniel L. Marks, and Stephen A. Boppart. Nearinfrared dyes as contrast-enhancing agents for spectroscopic optical coherence tomography. Opt. Lett., 29(14):1647–1649, 2004. 13, 14, 46 [7] B. Hyle Park, Mark C. Pierce, Barry Cense, and Johannes F. de Boer. Jones matrix analysis for a polarization-sensitive optical coherence tomography system using fiber-optic components. Opt. Lett., 29(21):2512–2514, 2004. 13 [8] Adam M. Zysk, Freddy T. Nguyen, Amy L. Oldenburg, Daniel L. Marks, and Stephen A. Boppart. Optical coherence tomography: a review of clinical development from bench to bedside. Journal of Biomedical Optics, 12(5): 051403, 2007. 9, 13 BIBLIOGRAPHY 78 [9] U. Morgner, W. Drexler, F. X. Kärtner, X. D. Li, C. Pitris, E. P. Ippen, and J. G. Fujimoto. Spectroscopic Optical Coherence Tomography. Opt. Lett., 25 (2):111–113, 2000. 13, 46, 71 [10] Dirk J. Faber, Egbert G. Mik, Maurice C. G. Aalders, and Ton G. van Leeuwen. Light absorption of (oxy-)hemoglobin assessed by spectroscopic optical coherence tomography. Opt. Lett., 28(16):1436–1438, 2003. 14, 46 [11] Desmond Adler, Tony Ko, Paul Herz, and James Fujimoto. Optical coherence tomography contrast enhancement using spectroscopic analysis with spectral autocorrelation. Opt. Express, 12(22):5487–5501, 2004. 14, 46, 53, 64, 71 [12] Adam Wax, Changhuei Yang, Vadim Backman, Kamran Badizadegan, Charles W. Boone, Ramachandra R. Dasari, and Michael S. Feld. Cellular Organization and Substructure Measured Using Angle-Resolved Low-Coherence Interferometry. Biophys. J., 82(4):2256–2264, 2002. 14, 46, 53 [13] Robert C. Youngquist, Sally Carr, and D. E. N. Davies. Optical coherencedomain reflectometry: a new optical evaluation technique. Opt. Lett., 12(3): 158, 1987. 15 [14] K. Takada, I. Yokohama, K. Chida, and J. Noda. New measurement system for fault location in optical waveguide devices based on an interferometric technique. Appl. Opt., 26(9):1603, 1987. 15 [15] H. H. Gilgen, R. P. Novak, R. P. Salathe, W. Hodel, and P. Beaud. Submillimeter optical reflectometry. Journal of Lightwave Technology, 7:1225–1233, 1989. 15 [16] A. F. Fercher, K. Mengedoht, and W. Werner. Eye-length measurement by interferometry with partially coherent light. Opt. Lett., 13(3):186, 1988. 15 [17] Christoph K. Hitzenberger. Measurement of corneal thickness by low-coherence interferometry. Appl. Opt., 31(31):6637, 1992. 15 [18] X. Clivaz, F. Marquis-Weible, R. P. Salathe, R. P. Novak, and H. H. Gilgen. High resolution reflectometry in biological tissues. Opt. Lett., 17(1):4, 1992. 15 [19] J. M. Schmitt, A. Knuttel, and R. F. Bonner. Measurement of optical properties of biological tissues by low-coherence reflectometry. Appl. Opt., 32(30): 6032, 1993. 15 [20] A. Fercher, C. Hitzenberger, W. Drexler, G. Kamp, and H. Sattmann. In vivo optical coherence tomography. Amer. J. Ophthalmol, 116:113–114, 1993. 15 BIBLIOGRAPHY 79 [21] J. G. Fujimoto, M. E. Brezinski, G. J. Tearney, S. A. Boppart, B. E. Bouma, M. R. Hee, J. F. Southern, and E. A. Swanson. Optical biopsy and imaging using optical coherence tomography. Nature Med., 1:970–972, 1995. 15, 24 [22] J. M. Schmitt, A. Knuttel, M. Yadlowsky, and R. F. Bonner. Optical coherence tomography of a dense tissue: statistics of attenuation and backscattering. Phys. Med. Biol., 42:1427–1439, 1994. 15, 24 [23] B. E. Bouma and G. J. Tearney, editors. Handbook of Optical Coherence Tomography. Marcel Dekker, New York, 2001. 16, 25 [24] Max Born and Emil Wolf. Principles of Optics. Cambridge University Press, Cambridge, seventh edition, 1999. 16 [25] Eugene Hecht. Optics. Addison Wesley, New York, fourth edition, 2001. 16 [26] J. W. Goodman. Statistical Optics. Wiley Classics Library. John Wiley and Sons, New York, 1985. 20 [27] Joseph M. Schmitt and Gitesh Kumar. Optical Scattering Properties of Soft Tissue: A Discrete Particle Model. Appl. Opt., 37(13):2788–2797, 1998. 24 [28] Brett E. Bouma, Lynn E. Nelson, Guillermo J. Tearney, David J. Jones, Mark E. Brezinski, and James G. Fujimoto. Optical Coherence Tomographic Imaging of Human Tissue at 1.55µm and 1.81µm Using Er- and Tm-Doped Fiber Sources. Journal of Biomedical Optics, 3(1):76–79, 1998. 24, 25 [29] Parwane Parsa, Steven L. Jacques, and Norman S. Nishioka. Optical properties of rat liver between 350 and 2200 nm. Appl. Opt., 28(12):2325, 1989. 24 [30] Jean-Luc Boulnois. Photophysical processes in recent medical laser developments: A review. Lasers in Medical Science, 1(1):47–66, 1986. 9, 24 [31] C. K. Hitzenberger, A. Baumgartner, and A. F. Fercher. Dispersion induced multiple signal peak splitting in partial coherence interferometry. Optics Communications, 154:179–185, 1998. 24 [32] M. Kempe, A. Thon, and W. Rudolph. Resolution limits of microscopy through scattering layers. Optics Communications, 10:492–496, 1994. 24 [33] E.A. Chinn, S.R.; Swanson. Blindness limitations in optical coherence domain reflectometry. Electronics Letters, 29(23):2025–2027, 1993. 25 [34] J.M. Schmitt. Optical coherence tomography (OCT): a review. Selected Topics in Quantum Electronics, IEEE Journal of, 5(4):1205–1215, 1999. 11, 25, 26 BIBLIOGRAPHY 80 [35] D. J. Derickson, P. A. Beck, T. L. Bagwell, D. M. Braun, J. E. Fouquet, F. G. Kellert, M. J. Ludowise, W. H. Perez, T. R. Ranganath, G. R. Trott, , and S. R. Sloan. High-power, low-internal-reflection, edge emitting light-emitting diodes. Hewlett-Packard J., 46:43–49, 1995. 25 [36] C. F. Lin and B. L. Lee. Extremely broadband AlGaAs/GaAs superluminescent diodes. Appl. Phys. Lett., 71:1598–1600, 1997. 25, 26 [37] P. J. Poole, M. Davies, M. Dion, Y. Feng, S. Charbonneau, R. D. Goldberg, and I. V. Mitchell. The fabrication of a broad-spectrum light-emitting diode using high-energy ion implantation. IEEE Photon. Technol. Lett., 8:1145–1147, 1996. 25, 26 [38] Hsiao-Hua Liu, Po-Hsiu Cheng, and Jyhpyng Wang. Spatially coherent whitelight interferometer based on a point fluorescent source. Opt. Lett., 18(9):678, 1993. 25 [39] B. Bouma, G. J. Tearney, S. A. Boppart, M. R. Hee, M. E. Brezinski, and J. G. Fujimoto. High-resolution optical coherence tomographic imaging using a mode-locked T i : Al2 O3 laser source. Opt. Lett., 20(13):1486, 1995. 25 [40] G. J. Tearney, M. E. Brezinski, B. E. Bouma, S. A. Boppart, C. Pitris, J. F. Southern, and J. G. Fujimoto. In vivo endoscopic optical biopsy with optical coherence tomography. Science, 276:2037–2039, 1997. 25 [41] R. Paschotta, J. Nilsson, A. C. Tropper, and D. C. Hanna. Efficient superfluorescent light sources with broad bandwidth. Selected Topics in Quantum Electronics, IEEE Journal of, 3(4):1097–1099, 1997. 25 [42] Jon Y. Wang. Detection efficiency of coherent optical radar. Appl. Opt., 23 (19):3421, 1984. 26 [43] J. M. Schmitt, S. L. Lee, and K. M. Yung. An optical coherence microscope with enhanced resolving power in thick tissue. Optics Communications, 142: 203–207, 1997. 26 [44] G. Mie. Beitrage zur optik triiber medien speziell kolloidaler metallosungen. Ann. Phys., 25(2):377–445, 1908. 27 [45] L. T. Perelman, V. Backman, M. Wallace, G. Zonios, R. Manoharan, A. Nusrat, S. Shields, M. Seiler, C. Lima, T. Hamano, I. Itzkan, J. Van Dam, J. M. Crawford, and M. S. Feld. Observation of periodic fine structure in reflectance from biological tissue: a new technique for measuring nuclear size distribution. Phys. Rev. Lett., 80(3):627–630, 1998. 27, 53, 64 BIBLIOGRAPHY 81 [46] V. Backman, V. Gopal, M. Kalashnikov, K. Badizadegan, R. Gurjar, A. Wax, I. Georgakoudi, M. Mueller, C. Boone, R. Dasari, and M. Feld. Measuring cellular structure at submicrometer scale with light scattering spectroscopy. Selected Topics in Quantum Electronics, IEEE Journal of, 7(6):887–893, Nov/Dec 2001. ISSN 1077-260X. doi: 10.1109/2944.983289. 27, 64 [47] M. Wallace, L. T. Perelman, V. Backman, J. M. Crawford, M. Fitzmaurice, M. Seiler, K. Badizadegan, S. Shields, I. Itzkan, R. R. Dasari, J. Van Dam, and M. S. Feld. Endoscopic detection of dysplasia in patients with Barrett’s esophagus using light-scattering spectroscopy. Gastroenterology, 119(3):677– 682, 2000. 27 [48] V. Backman, M. B. Wallace, L. T. Perelman, J. T. Arendt, R. Gurjar, M. G. Muller, Q. Zhang, G. Zonios, E. Kline, T. McGillican, S. Shapshay, T. Valdez, K. Badizadegan, J. M. Crawford, M. Fitzmaurice, S. Kabani, H. S. Levin, M. Seiler, R. R. Dasari, I. Itzkan, J. Van Dam, and M. S. Feld. Detection of preinvasive cancer cells. Nature, 406:35–36, 2000. 27 [49] V. Backman, R. Gurjar, K. Badizadegan, I. Itzkan, R. Dasari, L. Perelman, and M. Feld. Polarized light scattering spectroscopy for quantitative measurement of epithelial cellular structures in situ. Selected Topics in Quantum Electronics, IEEE Journal of, 5(4):1019–1026, 1999. 27 [50] Adam Wax, Changhuei Yang, and Joseph A. Izatt. Fourier-domain lowcoherence interferometry for light-scattering spectroscopy. Opt. Lett., (14): 1230–1232. 27, 46 [51] Adam Wax, Changhuei Yang, Vadim Backman, Maxim Kalashnikov, Ramachandra R. Dasari, and Michael S. Feld. Determination of particle size by using the angular distribution of backscattered light as measured with lowcoherence interferometry. J. Opt. Soc. Am. A, 19(4):737–744, 2002. 27, 46 [52] J. Beuthan, O. Minet, J. Helfmann, M. Herrig, and G. Muller. The spatial variation of the refractive index in biological cells. Phys. Med. Biol., 41(3): 369–382, 1996. 27, 45 [53] P. Sloot, A. Hoekstra, and C. Figdor. Osmotic response of lymphocytes measured by means of forward light scattering: theoretical considerations. Cytometry, 9(6):636–641, 1988. 27, 45 [54] C. Bohren and D. Huffman. Absorption and Scattering of Light by Small Particles. Wiley Science Paperback Series. John Wiley and Sons, New York, 1998. 27, 37, 45, 47 BIBLIOGRAPHY 82 [55] H. C. Van de Hulst. Light Scattering by Small Particles. Dover Publications, New York, 1981. 27, 37, 47 [56] G. B. Arfken and H. J. Weber. Mathematical Methods for Physicists. Academic Press, 2005. 33 [57] A. L. Aden. Electromagnetic scattering from spheres with sizes comparable to the wavelength. J. Appl. Phys., 22:601–605, 1951. 44 [58] W. J. Wiscombe. Improved Mie scattering algorithms. Appl. Opt., 19(9):1505, 1980. 44 [59] B. Hermann, K. Bizheva, A. Unterhuber, B. Považay, H. Sattmann, L. Schmetterer, A. Fercher, and W. Drexler. Precision of extracting absorption profiles from weakly scattering media with spectroscopic timedomain optical coherence tomography. Opt. Express, (8):1677–1688. 46 [60] C. Xu, P. S. Carney, W. Tan, and S. A. Boppart. Light-scattering spectroscopic optical coherence tomography for differentiating cells in 3D cell culture. Proc. of SPIE, 6088(608804):1–10, 2006. 46, 53 [61] Chenyang Xu, P. Carney, and Stephen Boppart. Wavelength-dependent scattering in spectroscopic optical coherence tomography. Opt. Express, 13(14): 5450–5462, 2005. 46, 64 [62] J. M. Schmitt, S. H. Xiang, and K. M. Yung. Speckle in optical coherence tomography. Journal of Biomedical Optics, 4:99–105, 1999. 48 [63] JD Briers and AF Fercher. Retinal blood-flow visualization by means of laser speckle photography. Invest. Ophthalmol. Vis. Sci., 22(2):255–259, 1982. 48 [64] Hitoshi Fujii, Toshimitsu Asakura, Kunihiko Nohira, Yoshihisa Shintomi, and Takehiko Ohura. Blood flow observed by time-varying laser speckle. Opt. Lett., 10(3):104, 1985. 48 [65] Michael D. Stern. Laser doppler velocimetry in blood and multiply scattering fluids: theory. Appl. Opt., 24(13):1968, 1985. 48 [66] J. W. Goodman. Statistical properties of laser speckle pattern. Applied Physics, 9, 1984. 49 [67] Lester I. Goldfischer. Autocorrelation function and power spectral density of laser-produced speckle patterns. J. Opt. Soc. Am., 55(3):247, 1965. 49 BIBLIOGRAPHY 83 [68] G. J. Tearney, M. E. Brezinski, J. F. Southern, B. E. Bouma, M. R. Hee, and J. G. Fujimoto. Determination of the refractive index of highly scattering human tissue by optical coherence tomography. Opt. Lett., 20(21):2258, 1995. 52 [69] R. Leitgeb, M. Wojtkowski, A. Kowalczyk, C. K. Hitzenberger, M. Sticker, and A. F. Fercher. Spectral measurement of absorption by spectroscopic frequencydomain optical coherence tomography. Opt. Lett., 25(11):820–822, 2000. 53 [70] John Proakis and Dimitris Manolakis. Digital Signal Processing, Principles, Algorithms and Applications. Prentice Hall, 2006. 55 [71] P. Chaturvedi and M. Insana. Autoregressive Spectral Estimation in Ultrasonic Scatterer Size Imaging. Ultrasonic Imaging, 18:10–24(15), 1996. 57 [72] K.A. Wear, R.F. Wagner, and B.S. Garra. A comparison of autoregressive spectral estimation algorithms and order determination methods in ultrasonic tissue characterization. Ultrasonics, Ferroelectrics and Frequency Control, IEEE Transactions on, 42(4):709–716, Jul 1995. 57 [73] Petre Stoica and Randolph L. Moses. Introduction to Spectral Analysis. Prentice Hall, 1997. 57 [74] J. P. Burg. Maximum Entropy Spectral Analysis. PhD thesis, Stanford University, 1975. 58 [75] I. T. Jolliffe. Principal Component Analysis. Springer-Verlag, second edition, 2002. 60 [76] J. E Jackson. A User’s Guide to Principal Components. Wiley Series in Probability and Statistics. John Wiley and Sons, New York, 2003. 61 [77] L. S. Dolin. A theory of optical coherence tomography. Radiophysics and Quantum Electronics, 41(10):850–873, 1998. 71 [78] Ilya V. Turchin, Ekaterina A. Sergeeva, Lev S. Dolin, Vladislav A. Kamensky, Natalia M. Shakhova, and Rebecca Richards-Kortum. Novel algorithm of processing optical coherence tomography images for differentiation of biological tissue pathologies. Journal of Biomedical Optics, 10(6):064024, 2005. 71 [79] Lars Thrane, Harold T. Yura, and Peter E. Andersen. Analysis of optical coherence tomography systems based on the extended huygens–fresnel principle. J. Opt. Soc. Am. A, 17(3):484–490, 2000. 71 BIBLIOGRAPHY 84 [80] Robert N. Graf and Adam Wax. Temporal coherence and time-frequency distributions in spectroscopic optical coherence tomography. J. Opt. Soc. Am. A, 24(8):2186–2195, 2007. 71

Top subcategories

Top subcategories

Top subcategories

Top subcategories

Top subcategories

Top subcategories

Top subcategories

Top subcategories

Download Biomedical Imaging and Applied Optics Laboratory