* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 3-5 Proving Lines Parallel
Survey
Document related concepts
Transcript
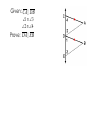
Advanced Geometry Parallel and Perpendicular Lines Lesson 3 Proving Lines Parallel Reasons Before we can prove that lines are parallel we need to add to our list of reasons. Corresponding Angles Postulate If two lines in a plane are cut by a transversal so that corresponding angles are congruent, then the lines are parallel. There are several theorems that can be proven using the Corresponding Angles Postulate. If two lines in a plane are cut by a transversal so that a pair of alternate exterior angles is congruent, then the two lines are parallel. To prove lines are parallel, you must use one of the following postulates or theorems: If corresponding angles are , then the lines are parallel. If AEA are , then the lines are parallel. If AIA are , then the lines are parallel. If CIA are supplementary, then the lines are parallel. You may also have to use the converse of a postulate or theorem to justify a statement. Given: 1 2 Prove: AB || CD Use the original theorem. If AIA are , the lines are ||. Given: AB || CD Prove: 1 2 Use the converse. If the lines are ||, AIA are . More Theorems If a line is perpendicular to one of two parallel lines, then it is perpendicular to the other. If two lines are perpendicular to the same line, then the lines are parallel. Given: m n and m p Prove: n p Given: 1 2 and 1 3 Prove: LM QN Given: CA DB 1 3 2 4 Prove: DA EB Given: PLM MNP NPL and PLM are supplementary. Prove: LP MN Given: WZ ZY and 1 2 Prove: WX WZ