Download GS 388 handout: Gravity Anomalies: brief summary 1 1. Observed

1
GS 388 handout: Gravity Anomalies: brief summary
1. Observed gravity is measured at a point of observation (Lat., Long., elevation) and is
generally a measurement of the difference between the gravity at the point of observation
and the gravity at one of the bench marks in a world-wide or national gravity network.
These benchmarks have been tied (again, by a measurement of relative gravity with a
geodetic gravimeter to cover a large range of gravity values) to one of the primary locations
where absolute gravity has been determined.
2. Calculate the gravity for a standard earth model at the point of observation:
a. Calculate the gravity at the latitude of the observation and at sea level directly
from an internationally agreed upon formula which gives gravity as a function of
latitude only. This formula takes into account the best determinations of the effects of
rotation, the spheroidal shape of the earth, and the mass of the earth, and specifies gravity
on the spheroidal equipotential reference surface which best approximates mean sea level.
b. Calculate the effect of moving from sea level to the elevation of the actual
observation location. This is the free air correction that you estimated in lab. For elevations
above sea level, the calculated gravity value is reduced.
c. Now calculate the effect of the mass between the elevated point of observation
and sea level. If this mass is simplified as an infinite slab of thickness equal to the
elevation, the calculated gravity will be increased by the attraction of this slab. Therefore
the theoretical gravity will be increased by 2πρ ch, where ρ c is the density of the slab
(density of the material above sea level) and h is elevation. This is called the simple
Bouguer correction and will lead to a "simple Bouguer anomaly". A more complicated
model of the topography can be used, taking into account nearby mass above the point of
observation and missing masses in valleys, etc., and will lead to a "terrain-corrected
Bouguer anomaly".
3. Two anomalies can be computed. One ignores the mass between the point of observation
and sea level (the "free air anomaly") while the other does not ("Bouguer anomaly").
For the free air anomaly the calculated gravity ignores the effect of mass above sea level:
g calc(lat,h) = g sph(lat, h=0) - FAC(h)
where g sph is the gravity from the standard formula, the minus sign applies to positive
elevation (height above sea level), and FAC(h) is the free air correction, i.e. the correction
for moving a distance h away from the center of the earth (which you derived in an earlier
lab). The free air anomaly, g FA , is given by
g FA = g obs(lat,h) - g calc(lat,h) = g obs(lat,h) - [g sph(lat) - FAC(h)]
g FA = g obs(lat,h) - g sph(lat) + FAC(h)
The simple bouguer anomaly takes into account the mass between the point of
observation and sea level to obtain a calculated gravity
g calc(lat,h) = g sph(lat, h=0) - FAC(h) + BGC(h,ρ c)
2
GS 388 handout: Gravity Anomalies: brief summary
where BGC(h,ρ c) is the effect of an infinite slab of material of thickness h and density ρ c
assumed to be located between the observation point and sea level. The simple Bouguer
anomaly, g BA , is given by
g BA = g obs(lat, h) - [g sph(lat) - FAC(h) + BGC(h,ρ c)]
g BA = g obs(lat, h) - g sph(lat) + FAC(h) - BGC(h,ρ c)
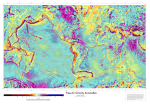
4. Gravity anomalies reflect anomalies in densities. A profile of gravity anomalies can be
generally fitted with a model of the distribution of positive and/or negative density
anomales in the crust and upper mantle. The effect of the density anomalies must be
calculated at the location of the points of observation. The calculated anomalies and the
observed anomalies are compared, and the model modified until the fit is satisfactory. The
main strategy is to estimate density contrasts across boundaries, and then use the shape of
the anomaly curve to help constrain the geometry of the boundaries.
5. A key approximation derives from the fact that the anomalies are very small compared to
the main field. Thus, the effect of the field of the anomalous masses upon the main field of
the earth is simplified as a projection of the anomaly field upon the standard field, rather
than a more tedious vector calculation (see diagram). For the gravity field (in contrast to the
magnetic field) this amounts to calculating the vertical component of the gravitational effect
of the anomalous masses: this is the component of the total field of the anomalies that is
projected onto the main field of the earth. The magnitude of the vertical component will be
to a good approximation the magnitude of the gravity anomalies.
3
GS 388 handout: Gravity Anomalies: brief summary
point of observation
gravity field due to
anomalous mass
α
g1
go
vector summation of
main field plus anomaly
field
main gravity field
of earth (without
anomalous mass)
anomalous mass
go + g1
The accurate anomaly value is the difference between the magnitude of the vector sum
(go+g1) and the magnitude of the vector go. It is easy to show (I leave it to you) that if the
magnitude of g1 is much smaller than go, then
calculated anomaly = |go+g1| - |go| ~ |g1| cos α = vertical component of g1
Note that in the figure the magnitude of the anomaly vector is greatly exaggerated- e.g., a
large gravity anomaly would be say 300 mg. which is only 3 parts in 10,000 relative to the
main field.