* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Field Lines Electric Flux
Survey
Document related concepts
Transcript
Gauss’ Law
Field Lines
Electric Flux
Recall that we defined
the electric field to be
the force per unit
charge at a particular
point:
For a source point charge Q and
a test charge q at point P
P
q
Q
at P
If Q is positive, then the
field is directed radially
away from the charge.
+
Note: direction of arrows
Note: spacing of lines
Note: straight lines
If Q is negative, then the
field is directed radially
towards the charge.
-
Negative Q implies
anti-parallel to
Note: direction of arrows
Note: spacing of lines
Note: straight lines
+
+
Field lines were introduced by Michael Faraday to help visualize the direction
and magnitude of the electric field. The direction of the field at any point is
given by the direction of the field line, while the magnitude of the field is given
qualitatively by the density of field lines. In the above diagrams, the simplest
examples are given where the field is spherically symmetric. The direction of
the field is apparent in the figures. At a point charge, field lines converge so
that their density is large - the density scales in proportion to the inverse of
the distance squared, as does the field. As is apparent in the diagrams, field
lines start on positive charges and end on negative charges. This is all
convention, but it nonetheless useful to remember.
-
+
This figure portrays several useful concepts. For example, near
the point charges (that is, at a distance that is small compared to
their separation), the field becomes spherically symmetric. This
makes sense - near a charge, the field from that one charge
certainly should dominate the net electric field since it is so
large. Along a line (more accurately, a plane) bisecting the line
joining the charges, we see that the field is directed along the -x
direction as shown.
+
+
In this case, we see the zero-field region precisely between the
two charges, and we also see a fairly rapid convergence on a
spherically symmetric distribution of field lines.
Example (Question)
The figure shows the electric field lines for a system of
two point charges.
(a) What are the relative magnitudes of the charges?
(b) What are the signs of the charges?
(c) In what regions of space is the electric field strong? weak?
Example (Solution)
The figure shows the electric field lines for a system of two point charges.
(a) What are the relative magnitudes of the charges?
(b) What are the signs of the charges?
(c) In what regions of space is the electric field strong? weak?
a) There are 32 lines coming from the
charge on the left, while there are 8
converging on that on the right. Thus,
the one on the left is 4 times larger than
the one on the right.
Example (Solution)
The figure shows the electric field lines for a system of two point charges.
(a) What are the relative magnitudes of the charges?
(b) What are the signs of the charges?
(c) In what regions of space is the electric field strong? weak?
• The one on the left is
positive; field lines leave
it. The one on the right is
negative; field lines end
on it.
Example (Solution)
The figure shows the electric field lines for a system of two point charges.
(a) What are the relative magnitudes of the charges?
(b) What are the signs of the charges?
(c) In what regions of space is the electric field strong? weak?
• The field is strong near both
charges. It is strongest on a line
connecting the charges. Few field
lines are drawn there, but this is
for clarity. The field is weakest to
the right of the right hand charge.
END
How would you measure 'the
density of electric field lines'
in a vicinity of space? First
think only of a discrete set of
electric field lines. One
obvious answer to the
question is that you would
count the number of lines
passing through an imaginary
geometrical (not real!)
surface.
The first two are
obvious, and the
following diagram
will indicate the
last:
The maximum number
of field lines is
intercepted when the
surface is perpendicular
to the field, while no
field lines will pass
through it when the
surface is parallel to the
field.
Uniform electric field - the
lines have constant density
and are all parallel
Surface is inserted in three
different orientations and
intersects the electric field
lines.
Number of
field lines
passing through
surface is large
Number of
field lines
passing through
surface is zero
Electric flux a function of surface
orientation, … relative to the electric field
Number of field
lines passing
through surface is
between zero and
the maximum.
Depends on the
orientation angle
θ.
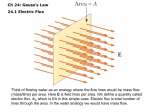
In general, the number of field lines passing through an area
A is directly proportional to cos(θ), where θ is the angle
between the electric field vector and the normal to the
surface vector.
Use this symbol to represent electric flux through a surface
Increasing surface area
Increasing electric field
The electric flux through the blue surface is the same in
these two figures. Electric flux is proportional to the
product of electric field and surface area A.
The number of field lines passing through a geometrical surface of given area
depends on three things: the field strength, the area, and the orientation of the
surface.
[E]-Electric field; Newton/Coulomb {N/C}
[A]-Surface area; meter2 {m2}
[θ]-Angle; degrees or radians {o, rad }
[ΦE]-Electric flux; Newton meter2/Coulomb {Nm2/C}
Example (Question)
A uniform electric field of 2.1 kN/C passes
through a rectangular area 22 cm by 28 cm. The field makes an
angle of 30o with the normal to the area. Determine the electric
flux through the rectangle.
Area A
Example (Solution)
A uniform electric field of 2.1 kN/C passes
through a rectangular area 22 cm by 28 cm. The field makes an
angle of 30o with the normal to the area. Determine the electric
flux through the rectangle.
2.1kN/C
30o
0.22 m X0.28 m = 0.062 m2
22 cm
28 cm
END
It is useful also to represent the area A by a vector. The
length of the vector is given by the area (a scalar
quantity), while the orientation is perpendicular to the
area. With this definition, the flux can be defined as:
recall
A slightly different notation for electric flux:
Unit vector perpendicular
to surface of area A
WHAT IF THE SURFACE IS CURVED AND/OR
THE FIELD VARIES WITH POSITION?
Element of surface area dA
q
Surface
Consider the surface as made up of
small elements over which the
electric field is uniform.
Flux for Non-Uniform Fields / Flux for Non-Uniform Surface
You might have noticed that all these equations really only work
for uniform electric fields.
We can use them here provided we make them pertain to
differential (small) area elements, and over a differential area
the field is uniform.
We then need to integrate (sum) to get the total flux through an
extended surface in a non-uniform field.
Flux for Non-Uniform Fields / Flux for Non-Uniform Surface
The differential electric flux passing through a differential
area is given by:
Element of surface area dA
As before, dA is a vector oriented perpendicular to the area, and the area itself is
differential (i.e., it's infinitesimally small and it's shape doesn't usually matter). The total
electric flux can be evaluated by integrating this differential flux over the surface.
Element of surface area dA
Flux for Non-Uniform Fields / Flux for Non-Uniform Surface
Flux for one segment
Surface
q
Total flux through surface
THE INTEGRAL IS TAKEN OVER
THE ENTIRE SURFACE.
Divide surface into small elements dA
THE BASIC DEFINITION OF
ELECTRIC FLUX
Example (Question)
A positive test charge of magnitude 3.0µC is
surrounded by a sphere with radius 0.20 m centered on the charge.
Find the electric flux through the sphere due to this charge.
+
At any point on the sphere the magnitude of
the electric field is:
+
Point charge electric field at
distance r from charge
E = 6.75 X 105 N/C
+
From symmetry the field is perpendicular to
the spherical surface at every point.
Same direction on the surface
+
The electric field has the same magnitude
over the spherical surface. It is thus constant
and may be taken outside the integral
The integral that remains is just the surface
area of the sphere.
The electric flux through the spherical surface is:
+
E = 6.75 X 105 N/C
END
Example (Question)
A positive test charge of magnitude 3.0µC is
surrounded by a sphere with radius 0.20 m centered on the charge.
Find the electric flux through the sphere due to this charge.
Consider the same
example again, but
this time we save the
calculations for the
end.
+
At any point on the sphere the magnitude of
the electric field is:
+
Point charge electric field at
distance r from charge
+
The electric field has the same magnitude
over the spherical surface. It is thus constant
and may be taken outside the integral
The integral that remains is just the surface
area of the sphere.
The electric flux through the spherical surface is:
+
q
ΦE =
εo
+
END
GAUSS’ LAW
Gauss' law is a generalization of the results discussed above
for the single charge and spherical surface.
It relates the electric flux passing through any surface
enclosing a charge distribution to the net charge enclosed.
GAUSS’ LAW
It relates the electric flux passing
through any surface enclosing a
charge distribution to the net
charge enclosed.
The flux through the two spheres
is the same since they enclose the
same charge.
GAUSS’ LAW
It relates the electric flux
passing through any surface
enclosing a charge
distribution to the net charge
enclosed.
The flux through the two
surfaces is the same since they
enclose the same charge.
GAUSS’ LAW
Each field line that enters the
surface also exits the surface.
+
The flux through the surface
is zero since no charge is
enclosed.
GAUSS’ LAW
Flux through spherical surface is
zero.
YOU CAN REASON
-
+
Each field line that exits the
surface eventually re-enters the
surface.
The net charge enclosed is zero.
+
IN GAUSS’ LAW, THE
CLOSED SURFACE IS
REFERRED TO AS A
GAUSSIAN SURFACE
USING GAUSS’
LAW
Gauss’ law is true for any surface enclosing any
charge distribution. When the charge distribution
has sufficient symmetry we can chose a surface --Gaussian Surface --- over which the evaluation
of the flux integral becomes simple. Gauss’ law
allows us to calculate the field far more easily than
we could using Coulomb’s law and superposition.
Using Gauss’ Law
Step 1: Study the symmetry to see if you
can construct a Gaussian surface on which
the field magnitude and its direction
relative to the surface are constant.
Through step 1 the dot product in the integral can
be replaced by:
Then Ecos(θ) is constant and can be removed from
inside the integral:
Using Gauss’ Law
Step 2: Evaluate the flux. This should be
easy because of your choice of the
Gaussian surface.
Using Gauss’ Law
Step 3: Evaluate the enclosed charge. This
is not the same as the total charge if the
Gaussian surface lies within the charge
distribution.
The Gaussian surface is an imaginary surface that you place in
the charge distribution. Choosing the Gauusian surface shape
and location depends on the symmetry of the charge
distribution AND on what exactly you want to calculate.
Using Gauss’ Law
Step 4: Equate the flux
and solve for E. The direction of the
electric field vector should be evident for
the symmetry and polarity of the charges.
In step 1 you reasoned the direction of E. Now go back and use that information.
ELECTRIC FIELD FROM A SPHERICAL CHARGE DISTRIBUTION.
Example (Question)
Charged sphere ρV
In this example we will follow the steps in
applying Gauss’ law in order to obtain an
expression for the electric field at a point
external to the uniform spherical charge
distribution.
R
Finding the electric field using Coulomb’s law
and superposition is lengthy and involves messy
math. Using Gauss’ law makes the task easy,
but, we must assume the field is radial.
Example (Solution)
ELECTRIC FIELD FROM A SPHERICAL CHARGE DISTRIBUTION.
Step 1: Study the symmetry to see if you can construct a Gaussian surface
on which the field magnitude and its direction relative to the surface are
constant.
Imaginary Gaussian surface (sphere of radius r)
Charged sphere ρV
Assume a radial
electric field
normal to
r
P
Example (Solution)
ELECTRIC FIELD FROM A SPHERICAL CHARGE DISTRIBUTION.
Step 2: Evaluate the flux. This should be easy because of your choice of
the Gaussian surface. The integral is just the area of the Gaussian
surface.
P
dA
Example (Solution)
ELECTRIC FIELD FROM A SPHERICAL CHARGE DISTRIBUTION.
Step 3: Evaluate the enclosed charge. This is not the same as the total
charge if the Gaussian surface lies within the charge distribution.
Imaginary Gaussian surface
Charged sphere ρV
All of the spherical charge distribution is
contained inside the spherical Gaussian
surface.
R
r
P
Total charge enclosed
Example (Solution)
ELECTRIC FIELD FROM A SPHERICAL CHARGE DISTRIBUTION.
Step 4: Equate the flux
and solve for E. The direction of the
electric field vector should be
evident for the symmetry and
polarity of the charges.
R
r
P
Example (Solution)
ELECTRIC FIELD FROM A SPHERICAL CHARGE DISTRIBUTION.
Combining results and solving for the electric field
P
Direction of E from
symmetry of charge
distribution
Example (Solution)
ELECTRIC FIELD FROM A SPHERICAL CHARGE DISTRIBUTION.
Combining results and solving for the electric field
Integral over charge distribution
R
r
P
Integral over Gaussian surface
SOLVING FOR THE ELECTRIC FIELD E
Example (Solution)
ELECTRIC FIELD FROM A SPHERICAL CHARGE DISTRIBUTION.
Writing electric field expression in terms of total
charge q inside Gaussian surface
Integral over charge distribution
R
r
P
Integral over Gaussian surface
SOLVING FOR THE ELECTRIC FIELD E
END
ELECTRIC FIELD FROM A SPHERICAL CHARGE DISTRIBUTION.
Example (Question)
Charged sphere ρV
In this example we will follow the steps in
applying Gauss’ law in order to obtain an
expression for the electric field at a point
internal to the uniform spherical charge
distribution.
R
Finding the electric field using Coulomb’s law
and superposition is lengthy and involves messy
math. Using Gauss’ law makes the task easy,
but, we must assume the field is radial.
Example (Solution)
ELECTRIC FIELD FROM A SPHERICAL CHARGE DISTRIBUTION.
Step 1: Study the symmetry to see if you can construct a Gaussian surface
on which the field magnitude and its direction relative to the surface are
constant.
Imaginary Gaussian surface (sphere of radius r)
Charged sphere ρV
R
Assume a radial
electric field
normal to
r
P
Example (Solution)
ELECTRIC FIELD FROM A SPHERICAL CHARGE DISTRIBUTION.
Step 2: Evaluate the flux. This should be easy because of your choice of
the Gaussian surface. The integral is just the area of the Gaussian
surface.
dA
Example (Solution)
ELECTRIC FIELD FROM A SPHERICAL CHARGE DISTRIBUTION.
Step 3: Evaluate the enclosed charge. This is not the same as the total
charge if the Gaussian surface lies within the charge distribution.
Imaginary Gaussian surface
Charged sphere ρV
R
r
P
Only the charge inside the Gaussian surface is
enclosed by the Gaussian surface. All charge
external to the Gaussian surface is not included.
Total charge
enclosed
Volume enclosed by
Gaussian surface
Example (Solution)
ELECTRIC FIELD FROM A SPHERICAL CHARGE DISTRIBUTION.
Step 3: Evaluate the enclosed charge. This is not the same as the total
charge if the Gaussian surface lies within the charge distribution.
Only the charge inside the Gaussian surface is
enclosed by the Gaussian surface. All charge
external to the Gaussian surface is not included.
R
r
P
External charge does not contribute to flux
External charge
Gaussian surface
E field lines intersect surface twice
contribution to flux cancel
Example (Solution)
ELECTRIC FIELD FROM A SPHERICAL CHARGE DISTRIBUTION.
Step 4: Equate the flux
r
R
and solve for E. The direction of the
electric field vector should be
evident for the symmetry and
polarity of the charges.
P
V = volume enclosed by Gaussian surface
Example (Solution)
ELECTRIC FIELD FROM A SPHERICAL CHARGE DISTRIBUTION.
Combining results and solving for the electric field
P
Direction of E from
symmetry of charge
distribution
Example (Solution)
ELECTRIC FIELD FROM A SPHERICAL CHARGE DISTRIBUTION.
Combining results and solving for the electric field
Integral over charge
distribution contained inside
Gaussian surface
r
R
P
Integral over Gaussian surface
SOLVING FOR THE ELECTRIC FIELD E
END
Electric field expression at a point outside and inside the
spherical charge distribution
R
r
R
r
P
P
INSIDE
OUTSIDE
Direction of E is radial
ELECTRIC FIELD FROM A INFINITE FLAT CHARGE DISTRIBUTION.
Example (Question)
Charged surface ρS
z
In this example we will follow the steps in
applying Gauss’ law in order to obtain an
expression for the electric field at a point
above a uniformly charged infinite flat
surface.
y
x
Finding the electric field using Coulomb’s
law and superposition is lengthy and
involves messy math. Using Gauss’ law
makes the task easy, but, we must assume
the field is uniform and normal to the flat
surface.
ELECTRIC FIELD FROM A INFINITE FLAT CHARGE DISTRIBUTION.
Example (Question)
Charged surface ρS
View of the flat
surface with
electric field
lines drawn.
Field is uniform
and normal to
the flat surface.
In this example we will follow the steps in
applying Gauss’ law in order to obtain an
expression for the electric field at a point
above a uniformly charged infinite flat
surface.
++
+
+
+
+
++
+
+
+
+
+
+
+
+
++
Example (Solution)
ELECTRIC FIELD FROM A INFINITE FLAT CHARGE DISTRIBUTION.
Step 1: Study the symmetry to see if you can construct a Gaussian
surface on which the field magnitude and its direction relative to the
surface are constant.
+
+
+
++
A1
+
++
A3
+
A
+
+
2
+
++
+
+
+
+
One possibility is to use
a cylindrical surface
with the top and bottom
surfaces parallel to the
charged plane. The E
field will be normal to
the top and bottom
surfaces.
The E field is parallel to the side of the cylinder and as such no field lines
(flux) pass through it.
This type of surface is often called a Gaussian pill box.
Example (Solution)
ELECTRIC FIELD FROM A INFINITE FLAT CHARGE DISTRIBUTION.
Step 2: Evaluate the flux. This should be easy because of your choice
of the Gaussian surface.
+
A1
+
+
+
++
Surface S contains
three parts (Top
A3, Bottom A1 and
Side A2)
+
+
A3
+
+ + +A2
+
+
+
++
+
Top
Bottom
Side
Example (Solution)
ELECTRIC FIELD FROM A INFINITE FLAT CHARGE DISTRIBUTION.
Step 2: Evaluate the flux. This should be easy because of your choice
of the Gaussian surface.
Top flux
++
+
+
+
A1
+
++
A3
+
A
+
++ 2
+
+
+
+
++
Uniform over A3
Outward pointing
parallel
Example (Solution)
ELECTRIC FIELD FROM A INFINITE FLAT CHARGE DISTRIBUTION.
Step 2: Evaluate the flux. This should be easy because of your choice
of the Gaussian surface.
Bottom flux
+
+
+
++
A1
+
++
A3
+
A
+
+
2
+
++
+
+
+
Uniform over A1
Outward pointing
+
parallel
Example (Solution)
ELECTRIC FIELD FROM A INFINITE FLAT CHARGE DISTRIBUTION.
Step 2: Evaluate the flux. This should be easy because of your choice
of the Gaussian surface.
Side flux
++
+
+
+
A1
+
++
A3
+
A
+
++ 2
+
+
+
+
++
Contained in side surface
Outward pointing
perpendicular
Example (Solution)
ELECTRIC FIELD FROM A INFINITE FLAT CHARGE DISTRIBUTION.
Step 2: Evaluate the flux. This should be easy because of your choice
of the Gaussian surface.
Top
Bottom
Total flux through Gaussian
surface is equal to flux through
top an bottom surfaces.
Side
+
+
+
+++
A2
+
+
+
A1 + + + A3
++
+
+
++
Example (Solution)
ELECTRIC FIELD FROM A INFINITE FLAT CHARGE DISTRIBUTION.
Step 3: Evaluate the enclosed charge. This is not the same as the
total charge if the Gaussian surface lies within the charge
distribution.
+
A1
+
+
+
++
+
+
A3
+
A
+
+
2
+
++
+
+
+
Charged surface ρS
Area A=A1=A3
+
The total charge
enclosed consists of only
the charge on the disk
contained within the
Gaussian Surface.
Disk of charged contained inside Gaussian
surface
Example (Solution)
ELECTRIC FIELD FROM A INFINITE FLAT CHARGE DISTRIBUTION.
Step 4: Equate the flux
and solve for E. The direction of the electric field vector should be
evident for the symmetry and polarity of the charges.
++
+
+
+
A1
+
++
A3
+
A
+
++ 2
+
+
+
+
++
Example (Solution)
ELECTRIC FIELD FROM A INFINITE FLAT CHARGE DISTRIBUTION.
Solve for electric field
++
+
+
+
A1
Direction of E determined
from symmetry
+
+
+
+
A
+
3
+ + A2
++
+
+
+
+
END
Example (Question)
ELECTRIC FIELD FROM A LONG STRAIGHT LINE OF CHARGE.
In one of the examples of lecture 2 we calculated the
magnitude and direction of the electric field from a long
straight line of charge using Coulomb’s law and superposition.
Now we will show how Gauss’ law can be used to obtain the
same result, in a few simple steps.
Uniform charge
density
Example (Solution)
ELECTRIC FIELD FROM A LONG STRAIGHT LINE OF CHARGE.
Step 1: Study the symmetry to see if you can construct a Gaussian
surface on which the field magnitude and its direction relative to the
surface are constant.
Imaginary Gaussian surface
Chose a cylinder of length
and radius R
E normal and constant to surface A2
E parallel and to surfaces A1 and A3
Example (Solution)
ELECTRIC FIELD FROM A LONG STRAIGHT LINE OF CHARGE.
Step 2: Evaluate the flux. This should be easy because of your choice
of the Gaussian surface.
Surface S contains
three parts (Front
A1, Back A3 and
Side A2)
Front
Back
Side
Example (Solution)
ELECTRIC FIELD FROM A LONG STRAIGHT LINE OF CHARGE.
Step 2: Evaluate the flux. This should be easy because of your choice
of the Gaussian surface.
Flux front
Contained in front surface
Outward pointing
perpendicular
Example (Solution)
ELECTRIC FIELD FROM A LONG STRAIGHT LINE OF CHARGE.
Step 2: Evaluate the flux. This should be easy because of your choice
of the Gaussian surface.
Flux back
Contained in back surface
Outward pointing
perpendicular
Example (Solution)
ELECTRIC FIELD FROM A LONG STRAIGHT LINE OF CHARGE.
Step 2: Evaluate the flux. This should be easy because of your choice
of the Gaussian surface.
Flux side
Normal to side surface (constant on surface)
Outward pointing
parallel
Example (Solution)
ELECTRIC FIELD FROM A LONG STRAIGHT LINE OF CHARGE.
Step 3: Evaluate the enclosed charge. This is not the same as the
total charge if the Gaussian surface lies within the charge
distribution.
The total enclosed by the Gaussian surface is only the
segment of the line within the bounds of the front and back
surfaces.
Uniform charge
density
Example (Solution)
ELECTRIC FIELD FROM A LONG STRAIGHT LINE OF CHARGE.
Step 4: Equate the flux
and solve for E. The direction of the electric field vector should be
evident for the symmetry and polarity of the charges.
Uniform charge
density
Example (Solution)
ELECTRIC FIELD FROM A LONG STRAIGHT LINE OF CHARGE.
Step 4: Equate the flux and solve for E.
Example (Solution)
ELECTRIC FIELD FROM A LONG STRAIGHT LINE OF CHARGE.
Step 4: Equate the flux and solve for E. The direction of the electric
field vector should be evident for the symmetry and polarity of the
charges.
ρ
E=
εo A2
Surface area of a cylinder
Note R radial distance from
charged line
END