Download Lecture

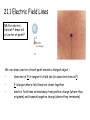
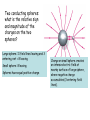
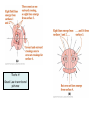
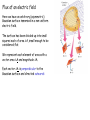
Gauss’s Law
Chapter 21
Summary Sheet 2
EXERCISE:
Draw electric field vectors
due to the point charge
shown, at A, B and C
C
.
B
.
+
Now draw field lines.
.A
In this chapter you’ll learn
•
•
•
•
To represent electric fields using
field-line diagrams
To explain Gauss’s law and how it
relates to Coulomb’s law
To calculate the electric fields for
symmetric charge distributions using
Gauss’s law (EASY!)
To describe the behavior of charge
on conductors in electrostatic
equilibrium
21.1 Electric Field Lines
NB For electric
field at P draw tail
of vector at point P
We can draw a vector at each point around a charged object •
direction of E is tangent to field line (in same direction as F)
•
E is larger where field lines are closer together
•
electric field lines extend away from positive charge (where they
originate) and towards negative charge (where they terminate)
Electric field lines provide a convenient and insightful way to
represent electric fields.
– A field line is a curve whose direction at each point is the
direction of the electric field at that point.
– The spacing of field lines describes the magnitude of the field.
• Where lines are closer, the field is stronger.
Vector and field-line
diagrams of a pointcharge field
The field lines for
two equal positive
charges
The field lines for two charges
equal in magnitude but opposite
in sign – an electric dipole
NB the electric field vector at a point is tangent to the
field line through the point
Field lines for simple charge distributions
There are field lines everywhere, so every charge
distribution has infinitely many field lines.
•
•
•
In drawing field-line
diagrams, we associate
a certain finite number
of field lines with a
charge of a given
magnitude.
In the diagrams shown,
8 lines are associated
with a charge of
magnitude q.
Note that field lines of
static charge
distributions always
begin and end on
charges, or extend to
infinity.
5.
Summary of electric
field lines
3.
Two conducting spheres:
what is the relative sign
and magnitude of the
charges on the two
spheres?
Large sphere: 11 field lines leaving and 3
entering, net = 8 leaving
Small sphere: 8 leaving
Spheres have equal positive charge
Charge on small sphere creates
an intense electric field at
nearby surface of large sphere,
where negative charge
accumulates (3 entering field
lines).
Gauss’s Law
A new look at Coulomb’s Law
Flux
Flux of an Electric Field
Gauss’ Law
Gauss’ Law and Coulomb’s Law
A new look at Coulomb’s Law
A new formulation of Coulomb’s Law was derived
by Gauss (1777-1855).
It can be used to take advantage of symmetry.
For electrostatics it is equivalent to Coulomb’s
Law. We choose which to use depending on the
problem at hand.
Two central features are
(1)a hypothetical closed surface – a Gaussian
surface – usually one that mimics the symmetry
of the problem, and
(2) flux of a vector field through a surface
Gauss’ Law relates the electric
fields at points on a (closed)
Gaussian surface and the net
charge enclosed by that surface
A surface or arbitrary shape enclosing an electric
dipole.
As long as the surface encloses both charges, the
number of lines penetrating the surface from
inside is exactly equal to the number of lines
penetrating the surface from the outside, no
matter where the surface is drawn
A surface of arbitrary shape enclosing charges
+2q and -q. Either the field lines that end on –q do
not pass through the surface or they penetrate it
from the inside the same number of times as
from the outside.
The net number that exit is the same as that for
a single charge of +q, the net charge enclosed by
the surface.
The net number of lines out of any surface
enclosing the charges is proportional to the net
charge enclosed by the surface.
Gauss’ Law (qualitative)
That’s it!
Gauss’ Law in words and
pictures
21.2 Electric flux
• Electric flux quantifies the notion
“number of field lines crossing a
surface.”
– The electric flux  through a flat
surface in a uniform electric field
depends on the field strength E, the
surface area A, and the angle 
between the field and the normal to the
surface.
– Mathematically, the flux is given by
  EA cos  E  A.
• Here A is a vector whose
magnitude is the surface area A
and whose orientation is normal to
the surface.
Electric flux with curved surfaces and
nonuniform fields
• When the surface is curved or the field is nonuniform, we calculate
the flux by dividing the surface into small patches dA, so small that
each patch is essentially flat and the field is essentially uniform over
each.
– We then sum the fluxes
d   E  dA over each patch.
– In the limit of infinitely many
infinitesimally small patches,
the sum becomes a
surface integral:
   E  dA
Flux of an electric field
Here we have an arbitrary (asymmetric)
Gaussian surface immersed in a non-uniform
electric field.
The surface has been divided up into small
squares each of area A, small enough to be
considered flat.
We represent each element of area with a
vector area A and magnitude A.
Each vector A is perpendicular to the
Gaussian surface and directed outwards
Electric field E may be assumed to be
constant over any given square
Vectors A and E for each square make an
angle  with each other
Now we could estimate that the flux of
the electric field for this Gaussian
surface is
 =  E  A
CHECKPOINT: Gaussian cube of
face area A is immersed in a
uniform electric field E that has
positive direction along z axis.
In terms of E and A, what is the
flux through …..
..the front face (in the xy plane)?
A. +EA
..the rear face?
B. 0
A. +EA ..the top face?
C. -EA
..the whole cube?
B. 0
A. +EA
A. +EA
C. -EA
B. 0
B. 0
C. -EA
C. -EA
Answers:
(a) +EA
(b) –EA
(c) 0
(d) 0
The flux through side B of the cube in the figure is the same
as the flux through side C. What is a correct expression for
the flux through each of these sides?
A.
B.
C.
D.
 s 3 E
  s2 E
  s3 E cos45
  s2 E cos45
End of Lecture 5