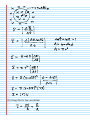Download Lecture Notes and Solved Problems

Chapter 22 Electromagnetic Induction
Wednesday, March 24, 2010
3:16 PM
In this chapter we continue our study of the connections between
electricity and magnetism. In the previous chapter (Chapter 21)
we learned that
• an electric current creates a magnetic field
• a magnetic field exerts a force on a moving charged particle
In this chapter we learn that a changing magnetic field creates
("induces") an electric field. (More accurately, a changing
magnetic flux creates ("induces") an electric field. We'll learn
about magnetic flux later in this chapter.) If a wire is nearby, the
induced electric field causes a current to flow in the wire. Thus, a
changing magnetic field induces a current in a conductor. This is
the main process that we use to produce electricity on a mass
scale.
Note that the textbook speaks of an induced emf, Ɛ; remember
that emf is a potential difference ("voltage difference"), which
provides an alternative, equivalent description of an electric field
E. Remember that the induced emf and the induced electric field
are distinct representations of the same phenomenon; they have
different units, and are different quantities, so don't confuse
them.
Ch22L Page 1
Ch22L Page 2
Ch22L Page 3
Ch22L Page 4
____________________________________________________
Example: A uniform magnetic field of magnitude 0.73 T is parallel
to the axis of a circular loop of wire of radius 8.5 cm. (That is, the
loop has radius 8.5 cm, not the wire!)
(a) Determine the induced emf in the wire if the magnetic field is
suddenly (i.e., in 0.01 s) turned off.
(b) Determine the current in the wire if the wire's resistance is
0.062 Ω.
Solution: (a) Use Faraday's law of induction.
Ch22L Page 5
(b) Using Ohm's law, we obtain
Ch22L Page 6
_________________________________________________________
Problem: Magnetic resonance imaging (MRI) is a medical technique for
producing "pictures" of the interior of the body. The patient is placed
within a strong magnetic field. One safety concern is what would
happen to the positively and negatively charged particles in the body
fluids if an equipment failure caused the magnetic field to be shut off
suddenly. An induced emf could cause these particles to flow, producing
an electric current within the body. Suppose the largest surface of the
body through which flux passes has an area of 0.032 m2 and a normal
that is parallel to a magnetic field of 1.5 T. Determine the smallest time
period during which the field can be allowed to vanish if the magnitude
of the average induced emf is to be kept less than 0.010 V.
Solution: Use Faraday's law of induction.
Ch22L Page 7
This is a large enough time to be of serious concern. The MRI
operators must be careful not to abruptly shut the power off, and
power failures must be avoided. To keep things safe, the magnet
should be turned off over a time period of at least 10 s or so, as one
always builds in a safety cushion.
__________________________________________________________
Problem: The magnetic flux that passes through one turn of a 12-turn
coil of wire changes to 4.0 Wb from 9.0 Wb in a time of 0.050 s. The
average induced current in the coil is 230 A. What is the resistance of
the wire?
Solution: Use Faraday's law of induction to determine the induced emf,
then use Ohm's law to determine the resistance of the wire.
Ch22L Page 8
________________________________________________________
Ch22L Page 9
Ch22L Page 10
Ch22L Page 11
Ch22L Page 12
Bicycle generator (for a headlight)
Geothermal Power Generator
Ch22L Page 13
Hydroelectric power generator
Ch22L Page 14
______________________________________________
Transformers
Ch22L Page 15
________________________________________________
Problem: The adaptor for my laptop converts 120 V AC to 19 V
AC, and then to 19 V DC. We won't bother with the AC to DC
conversion, which is beyond the scope of this course; just
focus on the step-down AC transformation.
(a) Determine the ratio of the number of turns in the primary
and secondary coils of the transformer.
(b) Determine the ratio of the currents in the primary and
secondary coils.
Solution:
Ch22L Page 16
Solution:
Thus, for example, if N2 is 100, then N1 is 630.
The current is higher in the secondary coil, by a factor of 6.3.
_________________________________________________
Ch22L Page 17
_________________________________________________
Problem: (a) Determine the resistance of a 150-km-long
aluminum cable that has a cross-sectional area of 8 square
centimetres.
Your generating station produces 1500 MW of electric power and
you decide to transmit it along the cable of Part (a). Determine
the resistive power loss if the power is transmitted at
(b) 250 kV and 6 kA.
(c) 750 kV and 2 kA.
Solution: (a) The resistivity of aluminum is
Ch22L Page 18
Thus, the resistance of the cable is
As a percentage of the generated power, the power loss is
As a percentage of the generated power, the power loss is
Ch22L Page 19
As a percentage of the generated power, the power loss is
Conclusion: Transmitting power with higher voltages and lower
currents decreases power losses. But this requires transforming
generated power to high voltages and then transforming back down to
lower voltages for use in homes and industries. This makes AC power
very practical, as transformers use AC current.
(This calculation is OK in broad outline, but it's incorrect in detail
because AC current tends to be transmitted near the skin of the cable,
and so the resistance calculation needs to be modified. You can deal
with this in your second-year electronics courses!)
________________________________________________________
Transformers provided a powerful tool with which George
Westinghouse (aided especially by Nikola Tesla, and his numerous
amazing inventions involving AC motors, generators, and other AC
electrical devices) won the "War of Currents" against Thomas
Edison. Tesla designed the Niagara Falls, NY electric power
generating station, among many other achievements.
Below is a photograph of a statue of Tesla in Queen Victoria Park
in Niagara Falls, ON.
Ch22L Page 20
_____________________________________________________
One of the significant problems with electrical power generation is
that it must be generated just when it is used. Sure, we can store
electrical energy using batteries, but the capacities of available
batteries is quite low. Battery technology is an active area of
research, and if someone could figure out an efficient way to store
large quantities of electrical energy this would be a terrific advance.
______________________________________________________
Problems and Solutions:
Problem: A 10-cm-long wire is pulled along a U-shaped
conducting rail in a perpendicular magnetic field. The total
resistance of the wire and rail is 0.20 Ω. Pulling the wire with
a force of 1.0 N causes 4.0 W of power to be dissipated in the
circuit. (a) Determine the speed of the wire. (b) Determine
the strength of the magnetic field.
Ch22L Page 21
Problem: Patients undergoing an MRI scan occasionally report
seeing flashes of light. Some practitioners assume that this
results from electrical stimulation of the eyes by the emf
induced by the rapidly changing fields of an MRI solenoid.
We can do a quick calculation to see if this is a reasonable
assumption. The human eyeball has a diameter of about 25
mm. Rapid changes in current in an MRI solenoid can
Ch22L Page 22
mm. Rapid changes in current in an MRI solenoid can
produce rapid changes in the magnetic field, with B/t as
large as 50 T/s. How much emf would this induce in a loop
circling the eyeball? How does this compare with the 15 mV
necessary to trigger an action potential?
Problem: A 1000-turn coil of wire 2.0 cm in diameter is in a
magnetic field that drops from 0.10 T to 0 T in 10 ms. The
axis of the coil is parallel to the field. Determine the emf in
the coil.
Problem: A 5.0-cm-diameter loop of wire has resistance 1.2
Ω. A nearby solenoid generates a uniform magnetic field
perpendicular to the loop that varies with time as shown in
the figure. Graph the magnitude of the current in the loop
Ch22L Page 23
the figure. Graph the magnitude of the current in the loop
over the same time interval.
Problem: A 100-turn, 8.0-cm-diameter coil is made of 0.50-mm
diameter copper wire. A magnetic field is perpendicular to the
coil. At what rate must B increase to induce a 2.0 A current in
the coil?
Ch22L Page 24
Problem: The loop in the figure is being pushed into the 0.20 T
magnetic field at a speed of 50 m/s. The resistance of the loop
is 0.10 Ω. Determine the direction and magnitude of the
current in the loop.
Ch22L Page 25