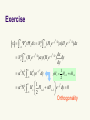Download powerpoint - University of Illinois Urbana

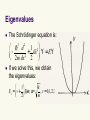
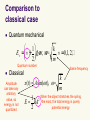
Lecture 10
Harmonic oscillator
(c) So Hirata, Department of Chemistry, University of Illinois at Urbana-Champaign. This material has
been developed and made available online by work supported jointly by University of Illinois, the
National Science Foundation under Grant CHE-1118616 (CAREER), and the Camille & Henry Dreyfus
Foundation, Inc. through the Camille Dreyfus Teacher-Scholar program. Any opinions, findings, and
conclusions or recommendations expressed in this material are those of the author(s) and do not
necessarily reflect the views of the sponsoring agencies.
Vibrational motion


Quantum-mechanical harmonic oscillator
serves as the basic model for molecular
vibrations. Its solutions are characterized by
(a) uniform energy separation, (b) zeropoint energy, (c) larger probability at
turning points.
We introduce the concept of orthogonal
polynomials. Here, we encounter the first
set: Hermite polynomials.
Differential equations
Differential equations
18th-19th century
mathematical
geniuses
Custom-made solutions:
Orthogonal polynomials
Know, verify, and use
the solutions (thankfully)
We
Vibrational motion



Quantum mechanical
version of a “spring and
mass” problem.
The mass feels the force
proportional to the
displacement:
F = – kx.
The potential energy is a
harmonic potential:
V = ½kx2 (F = –∂V/∂x).
Eigenvalues

The Schrödinger equation is:
2
2
æ
d
1 2ö
çè - 2m dx 2 + 2 kx̂ ÷ø Y = EY

If we solve this, we obtain
the eigenvalues:
æ
1ö
k
Ev = ç v + ÷ w , w =
, v = 0,1,2,…
2ø
m
è
Comparison to
classical case

Quantum mechanical
æ
1ö
k
Ev = ç v + ÷ w , w =
, v = 0,1,2,…
2ø
m
è
Quantum number

Classical
Amplitude
can take any
arbitrary
value, so
energy is not
quantized
Same frequency
k
x(t )  A sin(t ),  =
m
1 2 When the object stretches the spring
E  kA the most, the total energy is purely
potential energy
2
Comparison to
the particle in a box
The particle in a box
Harmonic potential
The energy levels

Zero-point energy
1
E0 = w
2

Energy separation
Molecules never cease to
vibrate even at 0 K –
otherwise the uncertainty
principle would be
violated.
Ev+1 - Ev = w
For molecular vibration, this amounts the energy of photon in
the infrared range. This is why many molecules absorb in the
infrared and get heated.
Quantum in nature
Vibrations of
CO2
Why is
global
warming?
Quantum in nature
Vibrations of
H2O
Why is water
blue?
Eigenfunctions

The eigenfunctions (wave functions) are
Y v (x) = N v ´ H v ( y) ´ e
- y 2 /2
æ ö
, y= , a =ç ÷
a
è mk ø
x
2
1/4
Gaussian function
Normalization
Hermite polynomial

We do not have to memorize this precise form but
we must remember its overall structure:
normalization coefficient x Hermite polynomial x
Gaussian function.
Orthogonal polynomials


The Hermite polynomials
are one example of
orthogonal polynomials.
They are discovered or
invented as the solutions
of important differential
equations. They ensure
orthogonality and
completeness of
eigenfunctions.
Hermite
Vibrational
wave function
Laguerre
Radial part of
atomic wave
function
Legendre
Angular part
of atomic
wave function
The Hermite polynomials
Ground-state
wave function

Since H0 = 1, the ground
state wave function is
simply a Gaussian function.
 0 ( x)  N 0 e
 y2 / 2
 N0 e
æ
ö
y= , a =ç
a
è mk ÷ø
x
2
 x2 / 2 2
1/4
The Hermite polynomials




The Hermite polynomials have the following
important mathematical properties:
They are the solution of the differential
equation:
2
d Hv
dH v
 2y
 2vH v  0
2
dy
dy
They satisfy the recursion relation:
H v 1  2 yH v  2vH v 1  0
Orthogonality 
y /2
y /2


 H e  H e dy  0, v  v
2
v
2
v
Verification

Second derivatives of a product of two
functions
2
2
æ
d
1 2ö
- y 2 /2
çè - 2m dx 2 + 2 kx ÷ø N v H v ( y)e
d ( fg ) df
dg

g f
dx
dx
dx
d 2 ( fg ) d 2 f
df dg
d 2g
 2 g2
f
2
dx
dx
dx dx
dx 2
Verification
Let us verify that this is indeed the
eigenfunction. Substituting

 0 ( x)  N 0 e
 y2 / 2
 N0 e
 x2 / 2 2
æ 2ö
y= , a =ç
a
è mk ÷ø
x
into the Schrödinger equation, we find
2
æ
d2 1 2ö
- x 2 /2a 2
=?
çè - 2m dx 2 + 2 kx ÷ø N 0e
2
2
de ax
d (ax 2 ) de ax
ax 2


(2
ax
)
e
dx
dx d (ax 2 )
2
d 2 eax
d
ax 2
ax 2
2 2 ax 2

(2
ax
)
e

2
ae

4
a
xe
dx 2
dx
1/4
Verification
Let us verify that this is indeed the
eigenfunction. Substituting

 0 ( x)  N 0 e
 y2 / 2
 N0 e
 x2 / 2 2
æ 2ö
y= , a =ç
a
è mk ÷ø
x
1/4
into the Schrödinger equation, we find
2
2
2
æ
æ
d2 1 2ö
x2
1 1 2ö
- x 2 /2a 2
- x 2 /2a 2
= ç+
+ kx ÷ N 0e
4
2
çè - 2m dx 2 + 2 kx ÷ø N 0e
2m a
2
è 2m a
ø
2
2
de ax
d (ax 2 ) de ax
ax 2


(2
ax
)
e
dx
dx d (ax 2 )
2
d 2 eax
d
ax 2
ax 2
2 2 ax 2

(2
ax
)
e

2
ae

4
a
xe
dx 2
dx
æ 1 2 1
= ç - kx +
2
è 2
1
- x 2 /2a 2
= w N 0e
2
k 1 2ö
- x 2 /2a 2
+ kx ÷ N 0e
m 2
ø
Zero point energy
Exercise

Calculate the mean displacement of the
oscillator when it is in a quantum state v.

Hint: Use the recursion relation to expose
vanishing integrals
H v 1  2 yH v  2vH v 1  0
Exercise

x    x v dx  N
*
v

N

2
v 

(H ve
 y2 / 2

2
v 

(H ve
) y ( H v e
 y2 / 2
 y2 / 2
) x( H v e
 y2 / 2
dx
) dy
dy
 N

2
v 
H ye
 N

2
v 
1
  y2
H v  H v 1  vH v 1  e dy  0
2

2
2


2
v
 y2
dy
)dx
1
yH v  H v 1  vH v 1
2
Orthogonality
Permeation of
wave functions
Probability in the
classically
forbidden region
gets smaller with
increasing v
(quantum
number). Another
correspondence
principle result.
v
Greater
probability near
the turning
points. Again
correspondenc
e to classical
case.
v
8 % of probability permeates into
the classically forbidden region.
Summary

The solution of the Schrödinger equation for
a harmonic potential or the quantummechanical harmonic oscillator has the
properties:



The eigenfunctions are a Hermite polynomial
times a Gaussian function.
The eigenvalues are evenly spaced with the
energy separation of ħω and the zero-point
energy of ½ħω.
The greater probability near the turning points for
higher values of v.