Download PDF of W2013 Midterm

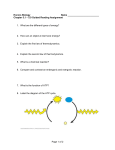
MIDTERM #1
PHYS 3511 (Biological Physics)
DATE/TIME: February 28, 2013 (11:30 a.m. – 12:45 p.m.)
PLACE: AT2006
Only non-programmable calculators are allowed.
Name: ___________________________________
ID: ___________________________________
Please read the following instructions:
• This midterm has 7 pages. Make sure none are missing.
• There are 2 parts.
• Part I consists of 5 multiple-choice question, each worth 4 points for a total
of 20 points. Do all questions.
• Part II consists of 4 full-answer questions, each worth 10 points for a total of
40 points. Do all works on the space provided below the questions.
• Rough work can be done on the back pages.
• Write your name and student ID in the provided space above.
• There is an equation sheet in the last page (page 7). You may tear the
equation sheet from the midterm.
Read questions carefully before attempting the solutions.
1
PART I: MULTIPLE CHOICE (question 1 to 5): Circle the one correct answer.
1. (4 points) Circle the one true biophysics statement.
a) In the diffusion equation r 2 = 6Dt , the diffusion coefficient, D, does not vary with
temperature.
b) Magnetotatic Bacteria have magnetic crystals making them internally similar to magnetic
compass needle.
c) The maculae are located in the ear and detect how fast the body is moving.
d) Organisms living in deep sea are subjected to high pressure. They are immediately
destroyed when pulled to the surface due to the lower concentration of salt.
e) The only difference between RNA and DNA is that the former is single stranded, and the
latter is double stranded.
2. (4 points) Circle the one true statement on how E. Coli swim.
a) The flagella motor of the E. Coli propagates the bacteria by ejecting water from a small
opening in its body
b) Small organisms, like E. Coli, cannot swim like large animals, since water is a very
viscous media for them. It would be like swimming in quicksand for humans
c) The rotation of the flagella of E. Coli is powered by ATP hydrolysis.
d) The shape (structure) of the flagella does not affect how fast the E. Coli swim.
3. (4 points) Circle the one true statement on ATP/ADP. When an ATP molecule splits,
forming an ADP molecule, the following physical change happens
a) The ATP molecule takes up energy
b) The ATP molecule exerts a force
c) The APT molecule does work
d) The ATP molecule releases energy
4. (4 points) A bacterium chromosomes have of DNA with molar mass 2.3 ! 10 9 g / mole with
average nucleotide basepair molar mass 618g / mole . Assume that the proteins in the
bacterium, on average, are made of 200 amino acid residues. Assuming there’s no junk gene
(the whole DNA is coding). The number of gene in this bacterium is closest to:
a) 18000 b) 6200
c) 3.7 ! 10 6
d) 1.2 ! 10 6
5. (4 points) Consider an isothermal process at T = 300K that expands two mole of gas from
volume Vi = 1L to V f = 3L . The initial pressure is P = 5000Pa . The change in internal
energy, !U , of the gas is closest to:
a) zero b) 5500 J c) !10000J d) 10000J
Hint: Assume this is an ideal gas with U =
3
k BT .
2
2
PART II: FULL ANSWER QUESTIONS (question 6 to 9): Show all works.
6. (10 points) An inexperience hawk of mass mh = 1.0kg attempts to hunt a monkey of mass
mm = 9.0kg sitting on a tree 9m above the ground. The hawk flies with a constant horizontal
velocity of v0 = 20m / s towards the monkey.
a) If the hawk is 15 m horizontally away from the monkey. How long does it take to reach
the monkey?
b) The hawk collides with the monkey and hold on to it with its claw. What is the
horizontal and vertical component of the velocity of the hawk and monkey right after the
collision? Hint: use conservation of momentum.
3
7. (10 points) A spherical bacterium of radius 100 µ m swims in water ! = 10 "3 kgim / s at a
constant speed of 3 ! 10 "3 m / s .
a) Calculate the minimum power produced by the bacteria to swim at this rate.
b) If the bacterium lives for 1 day, calculate the minimum number of ATP needed. Note:
Power is the energy produced per unit time (i.e. per second).
c) Give two possible reasons why the bacteria would need more than the amount ATP you
calculated in part b.
4
8. (10 points) Debunking the Levinthal’s paradox. A thermodynamics study at T = 25 !C of
the TrpCage protein found that when the protein unfolds from the native state (N) to the
unfolded state (U), the heat of reaction is !H = 56kJ / mol , with !H = H U " H N ,
with H U and H N being the Enthalpy of the U and N states, respectively. By data fitting it was
found !G = 3kJ / mol , where !G = GU " GN , with GU and GN being the Gibb’s free energy
of the U and N states, respectively.
a) Calculate !S = SU " SN , where SU and SN are the Gibb’s entropy of the U and N states,
respectively.
b) Use the definition Si = R ln !i , with R = 8.314J / K • mol , where !i is the number of
conformation per protein. Assuming that the number of conformations of the native state is
! N = 1 , find the number of conformations of the unfolded state !U .
c) Use the Levinthal’s argument, and assume that each conformation step, in the random
search to go from the U state to the single-conformation N state, takes about a picosecond or
10 !12 s . Estimate the average folding time of the Trpcage. Compare this with the actual
folding time of t fold = 4.0 µ s and to the estimated folding time suggested by Levinthal
Paradox.
5
9. (10 points) Model of the Lung Below is a simple diagram of the lung. The balloon
represents the alveoli, and the piston represents the diaphragm that can move in and out as
shown. The data below shows the pleura pressure (outside the alveoli, but inside the body).
Unit Note: 1L = 10 !3 m 3 , 1Pa = 1N / m 2
Inhaling Ppleura = !0.8kPa , and radius of alveoli
ralveoli = 58 µ m
Exhaling Ppleura = !0.5kPa , and radius of alveoli
ralveoli = 20 µ m
The pressure is the gauge pressure measured
with respect to the atmospheric pressure.
palveoli = 0 (its absolute pressure is 1 atm, same as
outside). This is because we assume the interior
of the alveoli is in contact with the outside.
(a) Based on above diagram and data, briefly explain the breathing mechanism of the lungs.
(b) Calculate the change in volume of the alveoli as the lung goes from exhale to inhale.
Assume the alveoli is a sphere.
(c) Assuming that during inhalation/exhalation the pressure is constant at p pleura = !0.65kPa ,
calculate the work done by the diaphragm to inflate one alveoli. What is the work done on the
air in the alveoli, when we exhale?
(d) In part c) we assume that the process is choose one: isothermal; isochoric; isobaric;
adiabatic.
6
Useful Equations
1
Kinematics x = x0 + v0 x t + a x t 2 , v x = v0 x + a x t , v x2 = v02x + 2a x (x ! x0 ), g = 9.8m / s 2 .
2
! net
!
!
!
Newton’s Laws F = ! F = 0 (equilibrium); F net = ma (Nonzero net force); 3rd Law if object
A exerts a force on object B, B exerts a force on A of equal magnitude and opposite in direction.
D
Friction f s ! µ s n , f k = µ k n . Fluid friction: 1) turbulent Fdrag = ! Av 2 ; 2) laminar
2
flow Fdrag = ! v (v speed), ! is drag coefficient; Stokes relation ! = 6"#r , r is the size, and ! is the
!
!
viscosity coefficient. Momentum: P = mv ; in a collision of isolated particles total momentum
!
!
!
dp
1
!
nd
is Ptotal = ! pi " constant; Newton 2 law in terms of momentum Fnet =
. KE = mv 2 ; work:
dt
2
i
! !
1
1
W = F • S = (F cos ! )s = F|| s ; W net = "K = mv 22 ! mv12 ( W net is net work); gravitational PE,
2
2
U PE = mgh ; conservation of energy Etotal = U PE + K ! constant.
Power = work/time; linear power P = Fv .
ATP hydrolysis (produces ADP) releases 29kJ/mol of heat. Reverse ADP ! ATP requires
29kJ/mol. POLYMER SIZE (DNA, RNA,..): rpolymer = 3N L .
THERMODYNAMICS:1st law !U = Q + W ; 2nd law isolated system evolves to state of
maximum entropy. Ideal gas PV = Nk BT , k B = 1.381 ! 10 "23 JiK "1 , or PV = nRT ,
3
3
R = 8.314Jimol !1 iK !1 ; Equipartition theorem U = Nk BT (monatomic gas) or U = nRT .
2
2
Vf
Work W = !P"V or W = ! " P dV ; PV = NkBT = nRT , kB = 1.381 ! 10 "23 J / K , R = 8.314
Vi
J/K*mol, Avogadro number N A = 6.023 ! 10 23 particle/mole . Isothermal
(
)
process !U = 0,W = NkBT ln Vi / V f ;Isobaric W = !P"V ; adiabatic PV 5 / 3 ! constant,
VT ! constant, Q = 0. U = (3 / 2)nRT . Entropy S = Q / T ; Enthalpy H = U + PV; Gibbs free
energy G = H ! TS , !G = !H " T !S , stable state has lowest Gibbs free energy; reaction is
spontaneous if !G < 0 . Temperature Kelvin to Celsius [ K ] = !" !C #$ + 273.15 . Pressure
3/2
1atm = 1.01325 ! 10 5 Pa ; Volume 1litre(L) = 10 !3 m 3
4
Sphere: V = ! r 3 ; A = 4! r 2 .
3
Stokes-Einstein Relation: drag coefficient ! = 6"# R ; diffusion coefficent D =
k BT
kT
= B ;
!
6"# R
Einstein diffusion: x 2 = 2Dt (1D), and r 2 = 6Dt (3D). Diffusion data D = 10 !9 m 2 / s for
small molecules like oxygen; ! = 10 "3 Pais for water, and for blood ! = 2.5 " 10 #3 Pais .
7