* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download The Wave Equation - NC State University
Noether's theorem wikipedia , lookup
Tight binding wikipedia , lookup
Canonical quantization wikipedia , lookup
Ensemble interpretation wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Coupled cluster wikipedia , lookup
Double-slit experiment wikipedia , lookup
Erwin Schrödinger wikipedia , lookup
Hydrogen atom wikipedia , lookup
Molecular Hamiltonian wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Copenhagen interpretation wikipedia , lookup
Renormalization group wikipedia , lookup
Path integral formulation wikipedia , lookup
Particle in a box wikipedia , lookup
Schrödinger equation wikipedia , lookup
Wave–particle duality wikipedia , lookup
Dirac equation wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Matter wave wikipedia , lookup
Probability amplitude wikipedia , lookup
Wave function wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
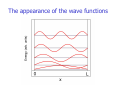
Chemistry 431 Lecture 3 The Schrödinger Equation The Particle in a Box (part 1) Orthogonality Postulates of Quantum Mechanics NC State University Derivation of the Schrödinger Equation The Schrödinger equation is a wave equation. Just as you might imagine the solution of such an equation in free space is a wave. Mathematically we can express a wave as a sine or cosine function. These functions are oscillating functions. We will derive the wave equation in free space starting with one of its solutions: sin(x). Before we begin it is important to realize that bound states may provide different solutions of the wave equation than those we find for free space. Bound states include rotational and vibrational states as well as atomic wave functions. These are important cases that will be treated once we have fundamental understanding of the origin of the wave equation or Schrödinger equation. The derivative The derivative of a function is the instantaneous rate of change. The derivative of a function is the slope. We can demonstrate the derivative graphically. We consider the function f(x) = sin(x) shown below. The derivative of sin(x) The derivative of a function is the instantaneous rate of change. The derivative of a function is the slope. At sin(0) the slope is 1 as shown by the blue line. The derivative of sin(x) The derivative of a function is the instantaneous rate of change. The derivative of a function is the slope. At sin(π/4) the slope is 1/√2 as shown by the blue line. The derivative of sin(x) The derivative of a function is the instantaneous rate of change. The derivative of a function is the slope. At sin(π/2) the slope is 0 as shown by the blue line. The derivative of sin(x) The derivative of a function is the instantaneous rate of change. The derivative of a function is the slope. At sin(3π/4) the slope is -1/√2 as shown by the blue line. The derivative of sin(x) The derivative of a function is the instantaneous rate of change. The derivative of a function is the slope. At sin(3π/4) the slope is -1/√2 as shown by the blue line. The slopes of all lines thus far are plotted as black squares. The derivative of sin(x) The derivative of a function is the instantaneous rate of change. The derivative of a function is the slope. At sin(π) the slope is -1 as shown by the blue line. The slopes of all lines thus far are plotted as black squares. The derivative of sin(x) The derivative of a function is the instantaneous rate of change. The derivative of a function is the slope. At sin(5π/4) the slope is -1/√2 as shown by the blue line. The slopes of all lines thus far are plotted as black squares. The derivative of sin(x) The derivative of a function is the instantaneous rate of change. The derivative of a function is the slope. At sin(5π/4) the slope is -1/√2 as shown by the blue line. The slopes of all lines thus far are plotted as black squares. The derivative of sin(x) The derivative of a function is the instantaneous rate of change. The derivative of a function is the slope. We see from of the black squares (slopes) that the derivative of sin(x) is cos(x). The derivative of sin(x) d sin(x) = cos(x) dx The derivative of cos(x) d cos(x) = -sin(x) dx The second derivative of sin(x) d dx d sin(x) = -sin(x) dx The second derivative of sin(x) d2 sin(x) = -sin(x) dx2 Sin(x) is an eigenfunction d2 If we define dx2 as an operator G then we have: d2 sin(x) = sin(x) dx2 which can be written as: G sin(x) = sin(x) This is a simple example of an operator equation that is closely related to the Schrödinger equation. Sin(kx) is also an eigenfunction We can make the problem more general by including a constant k. This constant is called a wavevector. It determines the period of the sin function. Now we must take the derivative of the sin function and also the function kx inside the parentheses (chain rule). d sin(kx) = -k cos(kx) dx d2 sin(kx) = k2sin(kx) dx2 Here we call the value k2 the eigenvalue. Sin(kx) is an eigenfunction of the Schrödinger equation The example we are using here can easily be expressed as the Schrodinger equation for wave in space. We only have to add a constant. -h2 d2 -h2k2 sin(kx) = sin(kx) 2m dx2 2m In this equation -h is Planck’s constant divided by 2π and m is the mass of the particle that is traveling through space. The eigenfunction is still sin(kx), but the eigenvalue in this equation is actually the energy. The Schrödinger equation Based on these considerations we can write a compact form for the Schrödinger equation. HΨ = EΨ -h2 d2 H=2m dx2 Energy operator, Hamiltonian -h2k2 E= 2m Energy eigenvalue, Energy Ψ= sin(kx) Wavefunction The momentum The momentum is related to the kinetic energy. Classically The kinetic energy is: 1 2 E = mv The momentum is: 2 p = mv So the classical relationship is: p2 E= 2m If we compare this to the quantum mechanical energy: -h2k2 E= 2m we see that: p = hk The general solution to the Schrödinger equation in free space The preceding considerations are true in free space. Since a cosine function has the same form as a sine function, but is shifted in phase, the general solution is a linear combination of cosine and sine functions. Ψ= Asin(kx) + Bcos(kx) Wavefunction The coefficients A and B are arbitrary in free space. However, if the wave equation is solved in the presence of a potential then there will be boundary conditions. The particle in a box problem Imagine that a particle is confined to a region of space. The only motion possible is translation. The particle has only kinetic energy. While this problem seems artificial at first glance it works very well to describe translational motion in quantum mechanics. 0 Allowed Region L The solution to the Schrödinger equation with boundary conditions Suppose a particle is confined to a space of length L. On either side there is a potential that is infinitely large. The particle has zero probability of being found at the boundary or outside the boundary. 0 Allowed Region L The solution to the Schrödinger equation with boundary conditions The boundary condition is that the wave function will be zero at x = 0 and at x = L. Ψ(0) = Asin(k0) + Bcos(k0) = 0 From this condition we see that B must be zero. This condition does not specify A or k. The second condition is: Ψ(L) = Asin(kL) = 0 or kL = arcsin(0) From this condition we see that kL = nπ. The conditions so far do not say anything about A. Thus, the solution for the bound state is: Ψn(x) = Asin(nπx/L) Note that n is a quantum number! The probability interpretation The wave function is related to the probability for finding a particle in a given region of space. The relationship is given by: P = Ψ 2dV If we integrate the square of the wave function over a given volume we find the probability that the particle is in that volume. In order for this to be true the integral over all space must be one. Ψ 2dV 1= all space If this equation holds then we say that the wave function is normalized. The normalized bound state wave function For the wave function we have been considering, all space is from 0 to L. So the normalization constant A can be determined from the integral: L 1= 0 L 2 Ψ dx = 0 A sin nπx L 2 2 dx = A L 2 0 sin nπx L 2 dx The solution to the integral is available on the downloadable MAPLE worksheet. The solution is just L/2. Thus, we have: 2 2 2 1=A L ,A = 2 ,A= L L 2 As you can see the so-called normalization constant has been determined. Normalization What is the normalization constant for the wave function exp(-ax) over the range from 0 to infinity? A. a B. 2a C. √a D. √2a Normalization What is the normalization constant for the wave function exp(-ax) over the range from 0 to infinity? A. a B. 2a C. √a D. √2a L 1= 0 ∞ Ψ 2dx = 0 ∞ 2 A 2exp – ax dx = A 2 2 = A 1 , A = 2a 2a 0 exp – 2ax dx The appearance of the wave functions The appearance of the wave functions Note that the wave functions have nodes (i.e. the locations where they cross zero). The number of nodes is n-1 where n is the quantum number for the wave function. The appearance of nodes is a general feature of solutions of the wave equation in bound states. By bound states we mean states that are in a potential such as the particle trapped in a box with infinite potential walls. We will see nodes in the vibrational and rotational wave functions and in the solutions to the hydrogen atom (and all atoms). Note that the wave functions are orthogonal to one another. This means that the integrated product of any two of these functions is zero. The energy levels The energy levels are: 2 2 n h E= 2 8mL The probability of finding the particle in a given region of space Using the normalized wave function Ψx = 2 sin nπx L L one can calculate the probability of finding the particle in any region of space. Since the wave function is normalized, the probability P is a number between 0 and 1. For example: What is the probability that the particle is between 0.2L and 0.4L. This is found by integrating over this region using the normalized wave function (see MAPLE worksheet). 0.4L 0.4L 2 2 nπx 2 P = Ψ x dx = sin dx ≈ 0.25 L L 0.2L 0.2L The appearance of the probability Ψ2 ö The probability of finding the particle in a given region of space Using the normalized wave function Ψx = 2 sin nπx L L one can calculate the probability of finding the particle in any region of space. Since the wave function is normalized, the probability P is a number between 0 and 1. For example: What is the probability that the particle is between 0.2L and 0.4L. This is found by integrating over this region using the normalized wave function (see MAPLE worksheet). 0.4L 0.4L 2 2 nπx 2 P = Ψ x dx = sin dx ≈ 0.25 L L 0.2L 0.2L Solutions of the Schrodinger equation are orthogonal If the wavefunctions have different quantum numbers Then their “overlap” is zero. We can call the integral Of the product of two wavefunctions an overlap. We write: L ΨmΨndx = δ mn 0 Where δmn is called the Kronecker delta. It has the property: δ mn = 0 if m ≠ n 1 if m = n For the particle-in-a-box the orthogonality is written: L 2 L 0 sin mπx sin nπx dx = δ mn L L Postulates of quantum mechanics are assumptions found to be consistent with observation The first postulate states that the state of a system can be represented by a wavefunction Ψ(q1, q2,.. q3n, t). The qi are coordinates of the particles in the system and t is time. The wavefunction can also be time-independent or stationary, ψ(q1, q2,.. q3n). Corollary: An acceptable wavefunction must be continuous and have a continuous first derivative Since the wavefunction is a solution of the Schrödinger equation it must be differentiable. The wavefunction must also be single-valued. Postulate 2. The probability of finding a particle in a region of space is given by a P(a) = Ψ Ψdτ ∗ 0 Assumptions for the Born interpretation 1. Ψ*Ψ is real (Ψ is Hermitian). 2. The wavefunction is normalized. 3. We integrate over all relevant space. Normalization is needed so that probabilities are meaningful Normalization means that the integral of the square of the wavefunction (probability density) over all space is equal to one. Ψ Ψdτ = 1 ∗ all space The significance of this equation is that the probability of finding the particle somewhere in the universe is one. Postulate 3. Every physical observable is associated with a linear Hermitian operator Observables are energy, momentum, position, dipole moment, etc. operator P → observable P The fact that the operator is Hermitian ensures that the observable will be real. Postulate 4. The average value of a physical property can be calculated by Ψ PΨdτ ∗ P = Normalization Ψ Ψdτ ∗ Postulate 4. The calculation of a physical observable can be written as an eigenvalue equation PΨ = PΨ This is an operator equation that returns the same wavefunction multiplied by the constant P. P is an eigenvalue. An eigenvalue is a number. The form of the operators is Position Momentum q P Time t Energy H q ∂ ih ∂q t ∂ ih ∂t Postulate 5. It is impossible to specify with arbitrary precision both the position and momentum of a particle This postulate is known as the Heisenberg Uncertainty Principle. It applies not only to the pair of variables position and momentum, but also to energy and time or any two conjugate variables. Conjugate variables are Fourier transforms of one another. Conjugate variables do not commute. Commutator in quantum mechanics A commutator is an operation that compares the order of operation for two operators: [ p,x] = px – x p Since the momentum, p involves a derivative, the order of application affects the result. The way to see the result of the commutator is to apply it to a test function f(x). pxf(x) = -ih(f(x) + xf’(x)) while xpf(x)= -ihxf’(x). Therefore [p,x] = - ih. We say that position and momentum do not Commute.