* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download FI17.HANDOUT.Bars Area Model Number Line
List of important publications in mathematics wikipedia , lookup
Mathematics and art wikipedia , lookup
Mathematics and architecture wikipedia , lookup
Philosophy of mathematics wikipedia , lookup
Mathematics wikipedia , lookup
History of mathematics wikipedia , lookup
Foundations of mathematics wikipedia , lookup
Critical mathematics pedagogy wikipedia , lookup
Ethnomathematics wikipedia , lookup
Secondary School Mathematics Curriculum Improvement Study wikipedia , lookup
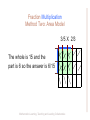
Fractions with Bars, Area Model and Number Line Mathematics Learning, Teaching and Leading Collaborative 1 The Structure of Fractions 3.NF 1. Understand a fraction 1/B as the quantity formed by 1 part when a whole is partitioned into B equal parts; B= 6 1/B 1/6 1/6 0/6 1/6 Mathematics Learning, Teaching and Leading Collaborative The Structure of Fractions 3NF 1. Understand a fraction A/B as the quantity formed by A parts of size 1/B.” 1/b 1/B = 1/6 1/6 1/6 A=0 and B=6 0/6 = 0 A= 4 4 parts of 1/6 = 4/6 A=4 B=6 4/6 A=6 and B=6 6/6 = 1 Mathematics Learning, Teaching and Leading Collaborative The Structure of Fractions 3NF 1. Understand a fraction 1/B as the quantity formed by 1 part when a whole is partitioned into B equal parts; understand a fraction A/B as the quantity formed by A parts of size 1/B.” 1/B = 1/12. The length of the blue line is A (in this case 4) parts of 1/B or 4 equal parts of 1/12; 1/12 + 1/12 + 1/12 + 1/12 = 4/12 • 1 Math Learning TLC Mathematics Learning, Teaching and Leading Collaborative The Structure of Fractions 3NF 2a. Represent a fraction 1/b on a number line diagram by defining the interval from 0 to 1 as the whole and partitioning it into b equal parts. Recognize that each part has size 1/b and that the endpoint of the part based at 0 locates the number 1/b on the number line. 3NF 2b. Represent a fraction a/b on a number line diagram by marking off a lengths 1/b from 0. Recognize that the resulting interval has size a/b and that its endpoint locates the number a/b on the number line. 0/6 1/6 1=6/6 Starting at 0, 1/6 it is reproduced 6 times to get a long segment equal to 6/6 or 1. The Main Topics of 4th Grade 4.NF A big idea in 4th grade is the fundamental facts about equivalent fractions (a fraction is not changed when its numerator and denominator are multiplied by the same nonzero whole number.) Spend time comparing, adding, and subtracting fractions with common denominators and the meaning of multiplying a fraction by a whole number. Math Learning TLC Mathematics Learning, Teaching and Leading Collaborative The fraction value is not changed when its numerator and denominator are multiplied by the same nonzero whole number. Or why 2/3 = 8/12 The square is vertically divided into three rectangles of equal area, and 2/3 of the area is represented by the thickened rectangle. n X a is equivalent to a nXb b 4X2= 8 4 X 3 = 12 2/3 = 8/12 Mathematics Learning, Teaching and Leading Collaborative (n × a)/(n × b) example: (4X2)/(4X3) = 8/12 2 = 4X2 3 4X3 2 = 8 3 12 2/3 2/3 4/4 If the square is vertically divided into three rectangles of equal area, then 2/3 is represented by the thickened rectangle. 8/12 The 2/3 is now divided horizontally into 4 parts of equal area, making a total of 12 congruent parts. The thickened rectangle now has a value of 8 parts out of 12 total parts or 8/12. Mathematics Learning, Teaching and Leading Collaborative Grade Four Fractions Examples from CCSS Content Standards for Mathematics 1) Break apart a fraction into smaller fractions with the same denominator, or bottom number, in more than one way. For example: 3⁄8 = 1 ⁄ 8 + 1 ⁄ 8 + 1 ⁄ 8 = 2 ⁄ 8+ 1 ⁄ 8 2) Explain why a fraction is equal to another fraction 3) Add and subtract mixed numbers (whole numbers mixed with fractions, such as 1 1/5) with the same denominators 4) Multiply a fraction by a whole number Mathematics Learning, Teaching and Leading Collaborative 9 Mathematics Learning, Teaching, & Leading Collaborative 10 Fraction Bars Individual Work 4.NF.1 Explain why a fraction a/b is equivalent to a fraction (n x a) / (n x b) by using visual fraction models, with attention to how the number and size of the parts differ . . . •Lay the 1/4 bar on your desk and then find bars with more parts but with the same amount of shading. Write down a number sentence to describe your actions. •Repeat this with the 1/2, 3/4, and 2/3 bars. When done, choose bars of your own choice, continue writing down number sentences that describe your actions. •Be ready to share your thinking and noticings. Mathematics Learning, Teaching and Leading Collaborative 11 Fraction Bars: Work and discuss in pairs, and then in your small group. 4.NF.1 Explain why a fraction a/b is equivalent to a fraction (n x a) / (n x b) by using visual fraction models, with attention to how the number and size of the parts differ . . . • Find the 1/2 bar. With your bars, show that 1/2 = 2/4 = 3/6 = 6/12 What do you notice? • Sketch a bar for 2/5. Divide the parts of your bar to show that 2/5 = 5/10. • Sketch a bar for 3/8. Divide the parts of your bar to show that 3/8 = 6/16. • What are some general methods you found for forming equivalent fractions? Be ready to report out to the large group. Mathematics Learning, Teaching and Leading Collaborative 12 Fraction Bars 4.NF.2 Compare 2 fractions with different numerators and different denominators . . . . . . . Locate the 1/3 fraction bar and the 1/4 fraction. Privately decide which fraction is greater and write down a number sentence that matches your thinking, using greater than or less then notation. Mathematics Learning, Teaching and Leading Collaborative 13 Fraction Bars 4.NF.2 Compare 2 fractions with different numerators and different denominators . . . . . . . Locate and lay out the following pairs of fraction bars. 1/2 and 4/6 5/12 and 2/3 5/6 and 7/12 2/3 and 3/4 Write down a number sentence for each pair using greater than or less than signs. Mathematics Learning, Teaching and Leading Collaborative 14 Fraction Bars Devise ways to use fraction bars to find these sums. Be ready to share your thinking. 4.NF.B Build fractions from unit fractions by applying and extending previous understandings of operations on whole numbers. 4.NF.B.3 Understand a fraction a/b with a > 1 as a sum of fractions 1/b. a) 1/5 + 2/5 = b) 3/4 + 2/4 = c) 3/6 + 4/6 = Mathematics Learning, Teaching and Leading Collaborative 15 Grade Five Fractions Examples from CCSS Content Standards for Mathematics 1) Interpret a fraction as division of the numerator (the top number) by the denominator (the bottom number) 2) Add and subtract fractions with different denominators 3) Multiply a fraction by a whole number or another fraction 4) Divide fractions by whole numbers and whole numbers by fractions Mathematics Learning, Teaching and Leading Collaborative 16 Fraction Bars Devise ways to use fraction bars to find these sums. Be ready to share your thinking. 5.NF.A Use equivalent fractions as a strategy to add and subtract fractions. 5.NF.A.1 Add and subtract fractions with unlike denominators (including mixed numbers) by replacing given fractions with equivalent fractions in such a way as to produce an equivalent sum or difference of fractions with like denominators. a) 2/3 + 3/4 = b) 2/3 + 5/6 = c) 3/4+ 3/12 = Mathematics Learning, Teaching and Leading Collaborative 17 Fraction Bars Devise ways to use fraction bars to find these differences. 5.NF.A.1 Add and subtract fractions with unlike denominators (including mixed numbers) by replacing given fractions with equivalent fractions in such a way as to produce an equivalent sum or difference of fractions with like denominators. a) 3/4 - 2/3 = b) 5/12 - 1/6 = c) 3/4 - 3/12 = d) 1 ½ - ⅚ = Mathematics Learning, Teaching and Leading Collaborative 18 Mathematics Learning, Teaching, & Leading Collaborative 19 Stop Go to “What is the product of 4 x 2/3? Mathematics Learning, Teaching, & Leading Collaborative 20 Grade Five Fractions Examples from CCSS Content Standards for Mathematics 1) Interpret a fraction as division of the numerator (the top number) by the denominator (the bottom number) 2) Add and subtract fractions with different denominators 3) Multiply a fraction by a whole number or another fraction 4) Divide fractions by whole numbers and whole numbers by fractions Mathematics Learning, Teaching and Leading Collaborative 21 Mathematics Learning, Teaching, & Leading Collaborative 22 Fraction Multiplication Method Two: Area Model 2/3 X 3/4 The square is vertically divided into three rectangles of equal area, and 2/3 is represented by the grey portion of the rectangle. The square is horizontally divided into four rectangles of equal area, and 3/4 is represented by the grey portion of the rectangle. Mathematics Learning, Teaching and Leading Collaborative Fraction Multiplication Method Two: Area Model 2/3 X 3/4 Now lay the 3/4 over the 2/3 Mathematics Learning, Teaching and Leading Collaborative Fraction Multiplication Method Two: Area Model 2/3 3/4 The shaded part of the rectangle is the part 3 X 2 = 6 (part) over the whole 4 X 3 = 12 (whole) 3 parts of equal area Mathematics Learning, Teaching and Leading Collaborative Fraction Multiplication Method Two: Area Model 3/5 X 2/3 The whole is 15 and the part is 6 so the answer is 6/15 Mathematics Learning, Teaching and Leading Collaborative Method Two Area Model Fraction Multiplication 3 1/2 X 4 = 14 AND 4 X 3 1/2 = 14 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1+ ½ + ½ + ½ + ½ = 12 + 4 (1/2) = 12 + 2 = 14 1 1 1 1/2 1 1 1 1/2 1 1 1 1/2 1 1 1 1/2 Math Learning TLC Mathematics Learning, Teaching and Leading Collaborative CCSS Math Task, Fraction Multiplication Rob is calculating the area of this rectangle. His strategy is to multiply the whole numbers first and then multiply the fractions. Since 6 X 7 = 42 and 1/2 × 6 = 3, he concludes that the area of the rectangle is 42 + 3 = 45 sq. units. Is he correct? If your answer is yes, explain why he correct. If you answer is no, write down the correct answer and tell why it is correct. 6 7 1/2 Math Learning TLC Mathematics Learning, Teaching and Leading Collaborative Mathematics Learning, Teaching, & Leading Collaborative 29 Mathematics Learning, Teaching, & Leading Collaborative 30 Mathematics Learning, Teaching, & Leading Collaborative 31 Mathematics Learning, Teaching, & Leading Collaborative 32 Mathematics Learning, Teaching, & Leading Collaborative 33 Fraction Multiplication, Method Three Egg Carton Fractions. Use your egg cartons and yarn to solve a selection (your choice) of the following. a) 1/4 of 2/3 e) 1/3 X 6/12 b) 1/3 of 2 f) 3/4 X 1 c) 3/4 of 1/3 g) 9/12 X 1/9 d) 1/4 of 1/3 h) 8/12 X 1/4 Mathematics Learning, Teaching, Mathematics Learning, TeachingCollaborative and Leading Collaborative & Leading 34 CCSS, 5th Grade Stuffed with Pizza Tito and Luis are stuffed with pizza! Tito ate one-fourth of a cheese pizza. Tito ate three-eights of a pepperoni pizza. Tito ate one-half of a mushroom pizza. Louis ate five-eights of the chees pizza. Louis ate the other half of the mushroom pizza. All the pizzas were the same size. Tito says he ate more pizza than Luis, because Luis did not eat any pepperoni pizza. Luis says they ate the same amount of pizza. • Who is correct? • Show all your mathematical thinking. Mathematics Learning, Teaching and Leading Collaborative 35